Numbers: Their Tales, Types, and Treasures.

Chapter 10: Numbers and Proportions

10.2.PROPORTIONS OF LENGTHS

Let us represent two magnitudes geometrically by lengths a and b. Consider, for example, the two line segments shown at the top of figure 10.3. How can we learn something about the relation between the two line segments—that is, about their proportion? If possible, we would like to find the natural numbers n and m, such that the proportion a:b could be expressed as n:m.

In order to achieve this, the Pythagoreans devised the following method, which we illustrate in figure 10.3.

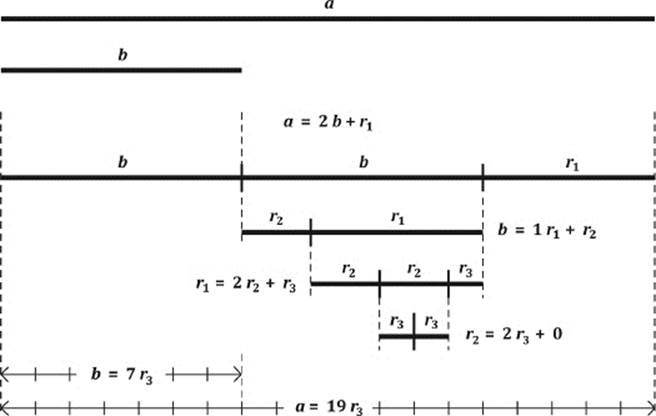
Figure 10.3: Determining the proportion of two line segments.

One starts by examining how often the shorter line segment b would fit into the longer one. Obviously, b fits into a twice, and then a short part r₁ of the segment a would be left over. Hence, we write a = 2 × b + r₁, where r₁ is shorter than b. The next question would be, how often wouldr₁ fit into b? Figure 10.3 shows that, obviously, b = 1 × r₁ + r₂, with r₂ < r₁. The next step shows that the remainder r₂ would fit into r₁ twice, with an even smaller remainder r₃. Finally, r₃ fits exactly twice into r₂. That is, there is no remainder r₄, or r₄ = 0.

What have we achieved now? Obviously, we found a length r₃ (the last nonvanishing remainder) that fits a whole number of times into all previous lengths, and, therefore, a = 19r₃, and b = 7r₃. Both line segments a and b can be expressed with the help of the small line segment r₃; they are both integer multiples of r₃. The line segment r₃ is a “unit” that allows us to measure a and b simultaneously and is called the “greatest common measure” of a and b. If r₃ would be taken as the unit of length, then we would have a = 19 and b = 7. We then say that a is to b in the same relation as 19 to 7. One says the proportion a:b equals 19:7. Today, this proportion would be considered a fraction with the numerical value of 19 divided by 7. In decimal notation this would be

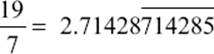
(the bar over the six digits after the point indicates that they are continuously repeated).

Greek philosophers in the fifth century BCE seemed to have held the belief that this method of finding an integer proportion would actually always work for any two quantities and would come to an end after a finite number of steps. Philosophers Leucippus and Democritus claimed that any extended continuous quantity cannot be divided infinitely. It was the birth of the theory of atomism—that is, that any division of an extended quantity would finally terminate in atoms, which cannot be further divided. Likewise, the method shown in figure 10.3 would terminate, in the worst case, when the remainder was the size of an atom and hence indivisible.