Numbers: Their Tales, Types, and Treasures.
Chapter 10: Numbers and Proportions
10.8.THE AMAZING HISTORY OF π
You may wonder how this famous ratio came to be represented by the Greek letter π. In 1706, English mathematician William Jones (1675–1749), in his book Synopsis Palmariorum Matheseos: or, A New Introduction to the Mathematics, used the symbol π for the first time to actually represent the ratio of the circumference of a circle to its diameter. However, the true popularity of the symbol π to represent this ratio came in 1748, when one of mathematics’ most prolific contributors, Swiss mathematician Leonhard Euler (1707–1783), used the symbol π in his bookIntroductio in Analysin Infinitorum to represent the ratio of the circumference of a circle to its diameter. A brilliant mathematician with an uncanny memory and ability to do complex calculations, Euler developed numerous methods for calculating the value of π, some of which approached the true value of π more quickly (that is, in fewer steps) than procedures developed by his predecessors. He calculated π to 126-place accuracy. The series below is particularly interesting, since it involves the reciprocals of the squares of all natural numbers:
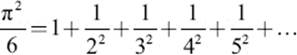
Multiplication by 6 and taking the square root would give you the value of π.
Many curiosities evolve from that number. For example, the quest to expand the decimal approximation of π to the largest number of places has been a fascinating challenge for centuries. You may ask, why do we need such accuracy for the value of π? We actually don't. If you want to compute the circumference of the whole observable universe from its radius (which is about 1027 m, the largest observable distance), you would need about sixty-two digits of π in order achieve a precision of a Planck length (10–35 m, the shortest observable distance). So the hunt for more digits has no practical purpose. The methods of calculation are simply used to check the accuracy and speed of the computer and the sophistication of the calculating procedure (sometimes referred to as an algorithm). That is, to determine how accurate and efficient the computer and software being tested is.
The current record for the most number of decimal places for the value of π is held by Alexander Yee and Shigeru Kondo, who used the software y-cruncher by Alexander Yee to compute 13.3 trillion digits in 2014. The number of digits of π will surely continue to increase.
It might be worthwhile to consider the magnitude of 13.3 trillion. How old do you think a person who has lived 13.3 trillion seconds might be? The question may seem irksome, since it requires having to consider a very small unit a very large number of times. However, we know how long a second is. But how big is one trillion? A trillion is 1,000,000,000,000, or one thousand billion. In one year there are 365 × 24 × 69 × 60 seconds. Therefore, 13.3 trillion seconds is equal to
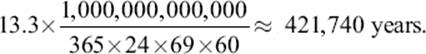
One would have to be in his 421,740th year of life to have lived 13.3 trillion seconds!
From these accurate approximations of π we might want to look back at some of the earliest estimates of π, which for many years was thought to be 3. One always relishes the notion that hidden codes can reveal long-lost secrets. Such is the case with the common interpretation of the value of π as 3 in the Bible. Let us look at one of the more amazing modern interpretations of ancient knowledge. There are two places in the Bible where the same sentence appears, identical in every way, except for one word, which is spelled differently in the two citations. The description of a pool or fountain in King Solomon's temple is referred to in the passages that may be found in 1 Kings 7:23 and 2 Chronicles 4:2, and it reads as follows:
And he made the molten sea of ten cubits from brim to brim, round in compass, and the height thereof was five cubits; and a line of thirty cubits did compass it round about.
The circular structure described here is said to have a circumference of 30 cubits and a diameter of 10 cubits. From this we notice that the Bible has 
. This is obviously a very primitive approximation of π. A late eighteenth-century rabbi, Elijah of Vilna (1720–1797), was one of the great modern biblical scholars, who earned the title “Gaon of Vilna” (meaning “brilliance of Vilna”). He came up with a remarkable discovery that, although the common interpretation of the value of π in the Bible was 3, brought the value of π in the Bible to much greater accuracy. Elijah of Vilna noticed that the Hebrew word for “line measure” was written differently in each of the two biblical passages mentioned above.
In 1 Kings 7:23 it was written as קוה, whereas in 2 Chronicles 4:2 it was written as קו. Elijah applied the ancient biblical analysis technique called Gematria, which is still used by Talmudic scholars today. This technique involves having the Hebrew letters take on their appropriate numerical values according to their sequence in the Hebrew alphabet. The letter values are: ק = 100, ו = 6, and ה = 5. Therefore, the spelling for “line measure” in 1 Kings 7:23 is קוה = 5 + 6 + 100 = 111, while in 2 Chronicles 4:2 the spelling קו = 6 + 100 = 106. Using the process of Gematria, he then took the ratio of these two values: 
(to four decimal places), which he considered the necessary “correction factor.” By multiplying the Bible's apparent value (3) of π by this “correction factor,” one gets 3.1416, which is π correct to four decimal places! “Wow!” is a common reaction. Such accuracy is quite astonishing for ancient times. If ten people were to take a piece of string and with it measure the circumference and diameter of some circular object and take their quotient, and then we take the average of these ten quotients, we would be hard-pressed to get the usual two-place accuracy, namely, π = 3.14. Now imagine getting π accurate to four decimal places—it might be nearly impossible with typical string measurements. Try it, if you need convincing.
On the other hand, the occurrence of the “correction factor” in the Bible could be pure coincidence. The two spellings of “line measure” also occur in other places in the Bible, in contexts where the correction factor seems to have no significance. Claims derived from Gematria are therefore not regarded as scientific. Whether or not you believe it also depends on the importance you attribute to the words in the Bible. Actually, it is rather improbable that a more accurate version of π was available at the time the biblical text was written (probably before 300 BCE). The greatest scholar of antiquity, Archimedes (ca. 267–212 BCE), found what was then the most accurate approximation of π, placing its value at
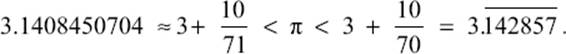
Archimedes arrived at these estimates by comparing the area of an inscribed polygon with the area of a circumscribed polygon, as shown in figure 10.14. In order to achieve this precision, he had to compute the circumference of the inscribed and circumscribed ninety-six-sided regular polygon.
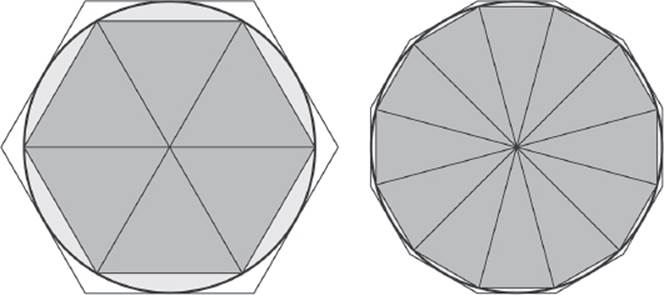
Figure 10.14: Approximation of circles by polygons.
The constant π is sometimes called Archimedes's constant because this algorithm was the best one to determine the value of π until modern times. Methods based on polygons were also used in ancient China, where, for example, Zu Chongzhi (428–500 CE) obtained a precision of seven digits by considering a 24,576-sided polygon. This was a record that held for over nine hundred years. In 1424, Persian astronomer and mathematician Jamshīd al-Kāshī (ca. 1380–1429) obtained an accuracy of nine sexagesimal digits (corresponding to an accuracy of sixteen digits in the decimal system) by computing the perimeter of a regular polygon with more than 800 million sides.
At about the same time, Indian astronomer and mathematician Madhava of Sangamagrame (ca. 1340–1425) invented a different method, which was based on the infinite sum
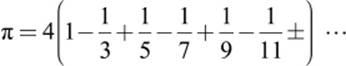
This beautiful representation of π was later rediscovered in Europe by Gottfried Leibniz (1646–1716) and is now called the Madhava-Leibniz formula. Madhava even found representations that were more useful in the actual computation of π and managed to determine π with a precision of eleven digits.
The next record was set by Ludolph van Ceulen (1540–1610) in about 1600. Using Archimedes's method, he approximated the circle using a regular polygon with 262 sides. This task occupied him for most of his life. In his honor, π is sometimes referred to as the Ludolphian number. His value of π is engraved onto his tombstone in St. Pieter's Kerk in Leiden, Holland.
Euler introduced more efficient methods to compute π, based on series expansions of the inverse tangent function. At the beginning of the twentieth century, Srinivasa Ramanujan (1887–1920) developed new expressions for π in the form of rapidly converging infinite sums, which later helped to design efficient algorithms for computers to compute the value of π. With the invention of the computer, the hunt for more digits continued and accelerated. In 1962, Daniel Shanks and his team published the first one hundred thousand digits, and the first billion digits were computed by David and Gregory Volfovich, known as the Chudnovsky brothers. Around 2000, Yasumasa Kanada and his team broke the 1 trillion digit threshold, which then led to the current record holders, Alexander Yee and Shigeru Kondo.
For a plethora of further information about the fascinating number π, we recommend the book Pi: A Biography of the World's Most Mysterious Number, by Alfred S. Posamentier and Ingmar Lehmann (Amherst, NY: Prometheus Books, 2004).