Numbers: Their Tales, Types, and Treasures.

Chapter 10: Numbers and Proportions

10.7.THE FAMOUS NUMBER π

In mathematics some numbers have taken on a special status. This can be the result of either their frequent appearance, or perhaps because enough observers have been enchanted by their special properties. The number that we will now consider seems to be most prevalent in the recollection of one's school mathematics. We are referring to the number that is typically represented by the Greek letter π. In mathematics, this letter is usually associated with either of the two formulas involving the circle—namely, the formula for the circumference of a circle (C = 2πr) and that for the area of a circle (A = πr²). The value that is usually associated with this letter π is 3.14. For some people, π is nothing more than a touch of the button on their pocket calculator, where, then, a particular number appears on the readout; for others, this number holds an unimaginable fascination. Depending on size of the calculator's display, the number shown might be

3.1415927, or
3.1415926535897932384626433832795, or even longer.

This push of a button still doesn't tell us what π actually is. We merely have a slick way of getting the decimal value of π. Actually, the number π represents a proportion: the ratio of the circumference of a circle to its diameter (see figure 10.12). As a proportion, it does not depend on the size of the circle.

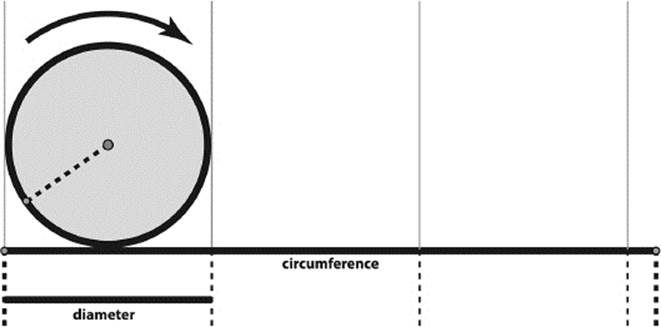
Figure 10.12: The proportion circumference:diameter is called π.

The number π is also the proportion between the area of the circle and the area of the square over the radius (see figure 10.13).

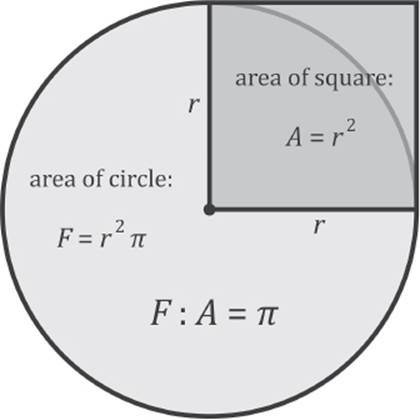
Figure 10.13: Proportion between areas of a circle and a square.

German mathematician Johann Heinrich Lambert (1728–1777) was the first to rigorously prove that π is irrational—that is, that π cannot be precisely represented as a fraction with integers in the numerator and denominator. His method of proof was to use a continued fraction expansion of the tangent function to show that if tan(x) is rational, then x cannot be rational. But if is a rational number, then , or π cannot be rational. In 1770 Lambert produced the following continued fraction for π.

Because π is an irrational number, the continued fraction would expand indefinitely. Inspecting this lengthy expression, we find that good approximations can be obtained if we end the expansion at some place with a large denominator. For example, we could replace the fraction with 292 in the denominator just by zero. This leads to the very good approximation

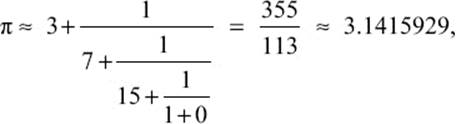
which differs from the actual value of π only in the seventh decimal place. This approximation is also easy to remember because the denominator and the numerator combine into the easily memorable pattern 113355.

For everyday purposes, we could end the expansion even earlier and use the approximation

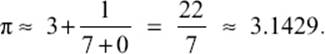
Computing the circumference of a circle with a diameter of 1 meter with this approximate value 3.1429 would create an error of about 1 mm.

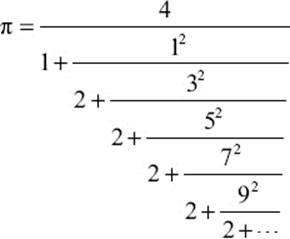
It is interesting that no obvious pattern has been discovered in the sequence of denominators in the continued fraction expansion. It can be proved that these numbers are not repeated periodically. This is related to the fact that π is a transcendental number—one that is not the solution of a nonzero polynomial equation with rational coefficients (unlike the golden ratio, ϕ, which is the solution of the polynomial equation ϕ² = ϕ + 1). On the other hand, there are different types of continued fraction expansions, which exhibit a striking regularity. The following result was obtained by English mathematician William Brouncker (1620–1684):

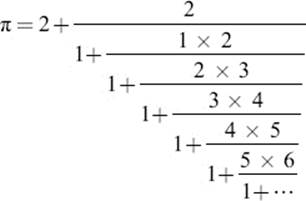
The following continued fraction was discovered in 1869 by James Joseph Sylvester (1814–1897), who is also known for his role in founding the American Journal of Mathematics:

In the decimal representation, the value of π can be expanded to an indefinite number of places. Mathematicians are always in search of patterns among these digits. So far, they have not found any pattern. It appears that the sequence of digits behaves like an arbitrary random sequence. Therefore, if you look far enough, you can find any given sequence of numbers of finite length among the decimal places of π. However, strange coincidences do occur. British mathematician John Conway (1937–) has indicated that if you separate the decimal expansion of π into groups of ten places, the probability of each of the ten digits appearing in any of these blocks is about 1 in 40,000. Yet he shows that it does occur in the seventh such group of ten places, as you can see from the grouping below:

π = 3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128….