Numbers: Their Tales, Types, and Treasures.

Chapter 10: Numbers and Proportions

10.6.INCOMMENSURABILITY

The simple observation presented in figure 10.10 seems to destroy the Pythagorean belief that all proportions can be expressed as proportions of natural numbers.

In section 10.2, we described a method of mutually marking off a shorter length on a longer line segment in order to express the proportion of two lengths a and b as a proportion of natural numbers. Let us now consider any two lengths that are in the proportion of the golden ratio—a:b =ϕ:1. Figure 10.10 clearly implies that the shorter segment b would fit just once into the longer segment a. The remainder is a – b. But b is in the same proportion to a – b as a is to b. All these segments are in the golden ratio ϕ:1. Unfortunately, this step has not brought us closer to finding the common unit of a and b. We have the same situation as in the beginning, namely two line segments in the proportion of the golden ratio. We could repeat that procedure indefinitely, and whenever you compare the shorter segment with the longer, it would just fit once, dividing the longer segment in the proportion of the golden ratio.

Hence the algorithm for finding a common unit for a and b would not terminate. There exists no common unit for two lengths that are in the proportion a:b = ϕ:1. We cannot find a line segment r, such that a = nr and b = mr with some natural numbers n and m. If expressed as a continued fraction, the proportion a:b would have the representation

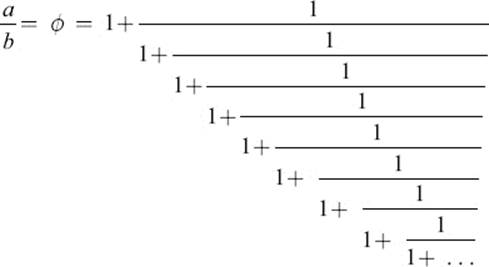
and this could be continued indefinitely. As we explained earlier, this just expresses the fact that b fits into a once, with a remainder that fits into b once, and so on. We could have seen this earlier, from the equation

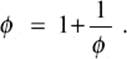
Inserting this very expression for ϕ into the denominator of the quotient on the right, we would obtain

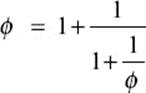
and we could repeat this process indefinitely, which would lead to the same infinite continued fraction as shown above:

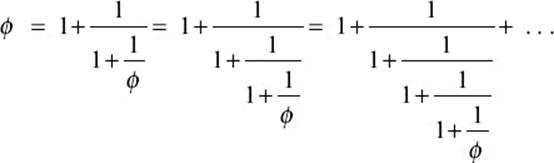
Any number that cannot be expressed as the ratio of two natural numbers is called irrational. From a more geometrical point of view, two lengths whose proportion a:b cannot be expressed as a ratio of integers are called incommensurable lengths, which means that there exists no common measure, that is, no common unit e such that a = ne and b = me. We mentioned this possibility in chapter 1, and now we have shown that it indeed occurs. If you try to measure the length ϕ, it is not possible to obtain it as a unit 1 plus a multiple of a fraction of that unit.

Among the real numbers, the rational numbers are the exception. There are so many irrational numbers that if you pick a random number on the number line, it would almost certainly be irrational. Likewise, two randomly chosen line segments in the plane would almost certainly be incommensurable.

A particularly famous example is the square root of two. This is the proportion between the side of a square and its diagonal. In Euclid's tenth book of his Elements, we find a number-theoretic proof of their incommensurability. The result was probably obtained much earlier, likely in the fifth century BCE. It is usually attributed to the Pythagorean philosopher Hippasus of Metapontum, who was a member of the Pythagorean order, for which the city Metapont was one of the centers in southern Italy (see chapter 4). One of the symbols of the Pythagorean order, the pentagram, was investigated around that time. The regular pentagram is formed by the diagonals of a regular pentagon. It turns out that the side of the pentagon and its diagonal are in the proportion of the golden ratio (see figure 10.11). Here, the indicated line segments are all in the proportion of the golden ratio: a:b = aʹ:bʹ = aʺ:bʺ = ϕ:1. It is ironic that Pythagoreans’ symbol, which is an apparent violation of their fundamental belief that everything can be expressed through proportions of natural numbers had always been right in their eyes.

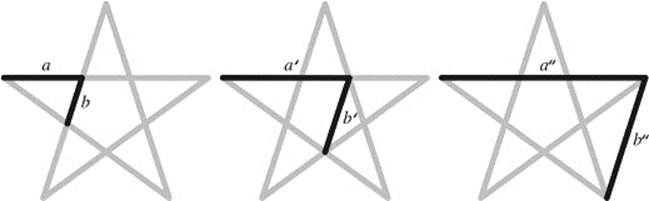
Figure 10.11: Golden proportions in the pentagram.

The golden ratio manifests itself in art and architecture as well as in nature. For a complete discussion of the golden ratio and its manifestations in geometry, its relationship to other famous numbers, and its many physical representations, we recommend the book The Glorious Golden Ratio, by Alfred S. Posamentier and Ingmar Lehmann (Amherst, NY: Prometheus Books, 2012).