Numbers: Their Tales, Types, and Treasures.
Chapter 10: Numbers and Proportions
10.5.THE GOLDEN RATIO
Although the proportion was already known in ancient Greece, the name “golden ratio” was coined in the nineteenth century by the German mathematician Martin Ohm (1792–1872). During the Renaissance, the Italian mathematician and Franciscan friar Luca Pacioli (1445–1517) called it the “divine proportion.” He wrote a book, De Divina Proportione, which contains illustrations by his friend Leonardo da Vinci (1452–1519). Moreover, Pacioli investigated proportions in nature, art, and architecture, and he explored the design principles behind the letters of the alphabet. The logo of the Metropolitan Museum of Art in New York City, showing the letter M, is based on one his designs (see figure 10.7).

Figure 10.7: Study of the letter M by Luca Pacioli, 1509.
Leonardo da Vinci is said to have incorporated the golden ratio ϕ, into some of his drawings and paintings—for example, his Vitruvian Man, a study of human proportions according to the Roman architect Vitruvius (see figure 10.8). Here, the ratio of the radius of the circle and the side of the square is approximately the golden ratio, ϕ.
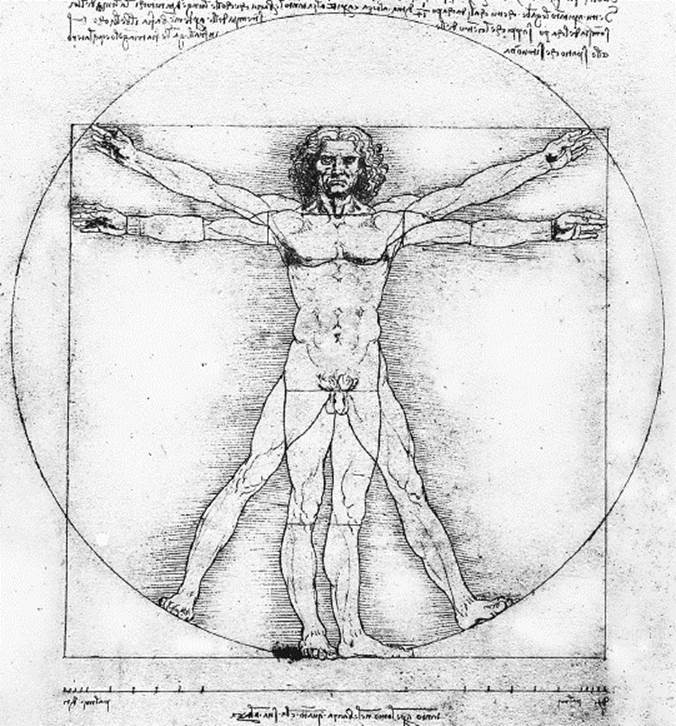
Figure 10.8: Leonardo da Vinci's Vitruvian Man, ca. 1490. (Original located at Campo della Carità, Dorsoduro 1050, Venice, Italy.)
A rectangle where the length a and width b are in the proportion a:b = ϕ:1, is called a golden rectangle, as shown in figure 10.9. The proportions of a golden rectangle can be approximated by the “Fibonacci rectangles” in figure 10.6 because ϕ:1 approximates Fn+1:Fn for large natural numbers n.
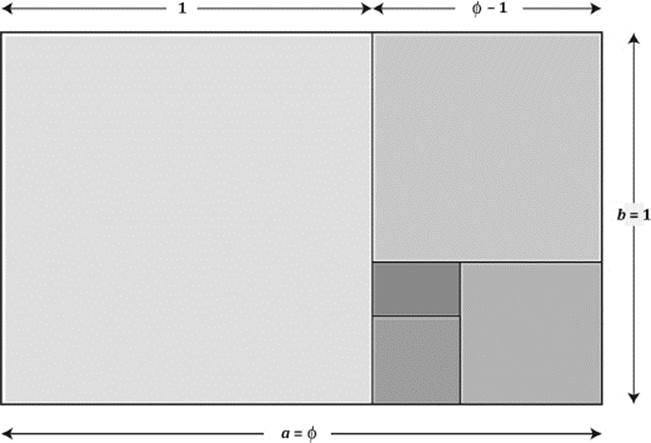
Figure 10.9: The golden rectangle.
The golden rectangle has the strange property that if we cut off a square, the remaining figure will again be a golden rectangle. This can be seen as follows. The remaining figure, as shown in figure 10.9, has the proportion 1:(ϕ – 1). Consider the following computation, which makes use of the “defining equation” ϕ2 = ϕ + 1, or ϕ2 – ϕ = 1:
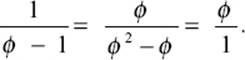
The proportion of the sides of the small rectangle is again ϕ:1. That makes the small rectangle again a golden rectangle.
The relation ϕ2 = ϕ + 1, which defines the golden ratio, also implies (upon dividing both sides by ϕ) that
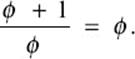
Consider a line segment divided into two parts, a and b, such that their proportion is a:b = ϕ:1, which is why the golden ratio is often called the golden section. (See figure 10.10.) The just-derived proportions,
1:(ϕ – 1) = ϕ:1 = (ϕ + 1):ϕ,
are the same if the two line segments are not of length ϕ and 1 but of length a and b, where a:b = ϕ:1. The equality of proportions above would then be equivalent to
b:(a – b) = a:b = (a + b):a.
Expressed as a proportion of two line segments, these relations are shown in figure 10.10, illustrating the following facts: If you cut a straight line into two segments a and b, in the proportion of the golden ratio, then
(a)the shorter line segment b divides the longer line segment a in the proportion of the golden ratio, that is, a:b = ϕ;
(b)the longer line segment a divides the sum a + b in the proportion of the golden ratio, that is, (a + b):a = ϕ; and
(c)the difference a – b divides the shorter line segment in the proportion of the golden ratio, that is, b:(a – b) = ϕ.
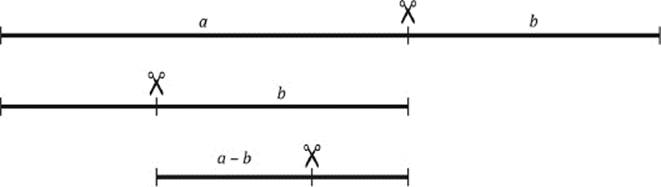
Figure 10.10: The golden section.