Mathematics, Substance and Surmise: Views on the Meaning and Ontology of Mathematics (2015)
Introduction
Ernest Davis1
(1)
Department of Computer Science, Courant Institute of Mathematical Sciences, New York University, New York, NY, USA
Ernest Davis
Email: davise@cs.nyu.edu
Mathematics discusses an enormous menagerie of mathematical objects: the number 28, the regular icosahedron, the finite field of size 169, the Gaussian distribution, and so on. It makes statements about them: 28 is a perfect number, the Gaussian distribution is symmetric about its mean. Yet it is not at all clear what kind of entity these objects are. Mathematical objects do not seem to be exactly like physical entities, like the Eiffel Tower; nor like fictional entities, like Hamlet; nor like socially constructed entities, like the English language or the US Senate; nor like structures arbitrarily imposed on the world, like the constellation Orion. Do mathematicians inventmathematical objects; or posit them; or discover them? Perhaps objects emerge of themselves, from the sea of mathematical thinking, or perhaps they “come into being as we probe” as suggested by Michael Dummett [1].
Most of us who have done mathematics have at least the strong impression that the truth of mathematical statements is independent both of human choices, unlike truths about Hamlet, and of the state of the external world, unlike truths about the planet Venus. Though it has sometimes been argued that mathematical facts are just statements that hold by definition, that certainly doesn’t seem to be the case; the fact that the number of primes less than N is approximately ![]() is certainly not in any way an obvious restatement of the definition of a prime number. Is mathematical knowledge fundamentally different from other kinds of knowledge or is it simply on one end of a spectrum of certainty?
is certainly not in any way an obvious restatement of the definition of a prime number. Is mathematical knowledge fundamentally different from other kinds of knowledge or is it simply on one end of a spectrum of certainty?
Similarly, the truth of mathematics—like science in general, but even more strongly—is traditionally viewed as independent of the quirks and flaws of human society and politics. We know, however, that math has often been used for political purposes, often beneficent ones, but all too often to justify and enable oppression and cruelty.1 Most scientists would view such applications of mathematics as scientifically unwarranted; avoidable, at least in principle; and in any case irrelevant to the validity of the mathematics in its own terms. Others would argue that “the validity of the mathematics in its own terms” is an illusion and the phrase is propaganda; and that the study of mathematics, and the placing of mathematics on a pedestal, carry inherent political baggage. “Freedom is the freedom to say that two plus two makes four” wrote George Orwell, in a fiercely political book whose title is one of the most famous numbers in literature; was he right, or is the statement that two plus two makes four a subtle endorsement of power and subjection?
Concomitant with these general questions are many more specific ones. Are the integer 28, the real number 28.0, the complex number 28. 0 + 0i, the 1 × 1 matrix [28], and the constant function f(x) = 28 the same entity or different entities? Different programming languages have different answers. Is “the integer 28” a single entity or a collection of similar entities; the signed integer, the whole number, the ordinal, the cardinal, and so on? Did Euler mean the same thing that we do when he wrote an integral sign? For that matter, do a contemporary measure theorist, a PDE expert, a numerical analyst, and a statistician all mean the same thing when they use an integral sign?
Such questions have been debated among philosophers and mathematicians for at least two and a half millennia. But, though the questions are eternal, the answers may not be. The standpoint from which we view these issues is significantly different from Hilbert and Poincaré, to say nothing of Newton and Leibnitz, Plato and Pythagoras, reflecting the many changes the last century has brought. Mathematics itself has changed tremendously: vast new areas, new techniques, new modes of thought have opened up, while other areas have been largely abandoned. The applications and misapplications of mathematics to the sciences, technology, the arts, the humanities, and society have exploded. The electronic computer has arrived and has transformed the landscape. Computer technology offers a whole collection of new opportunities, new techniques, and new challenges for mathematical research; it also brings along its own distinctive viewpoint on mathematics.
The past century has also seen enormous growth in our understanding of mathematics and mathematical concepts as a cognitive and cultural phenomenon. A great deal is now known about the psychology and even the neuroscience of basic mathematical ability; about mathematical concepts in other cultures; about mathematical reasoning in children, in pre-verbal infants, and in animals.
Moreover the larger intellectual environment has altered, and with it, our views of truth and knowledge generally. Works such as Kuhn’s analysis of scientific progress and Foucault’s analysis of the social aspects of knowledge have become part of the general intellectual currency. One can decide to reject them, but one cannot ignore them.
This book
The seventeen essays in this book address many different aspects of the ontology and meaning of mathematics from many different viewpoints. The authors include mathematicians, philosophers, computer scientists, cognitive psychologists, sociologists, historians, and educators. Some attack the ontological problem head on and propose a specific answer to the question, “What is a mathematical object?”; some attack it obliquely, by discussing related aspects of mathematical thought and practice; and some argue that the question is either useless or meaningless.
It would be both unnecessary and foolhardy to attempt to summarize the individual chapters. But it may be of interest to note some common themes:
· The history of math, mathematical philosophy, and mathematical practice. (Avigad, Bailey & Borwein, Gillies, Gray, Lützen, O’Halloran, Martin & Pease, Ross, Stillwell, Verran). Among scientists, mathematicians are particularly aware of the history of their field; and philosophers sometimes seem to be aware of little else. Many different aspects and stages in the evolution of thinking about mathematics and its objects are traced in these different essays.
· The real line and Euclidean geometry (Bailey & Borwein, Berlinski, E. Davis, Gillies, Gray, Lützen, Stillwell). These essays in the collection touch on many different mathematical theories and objects, but the problems associated with ![]() and
and ![]() seem particularly prominent.
seem particularly prominent.
· The role of language (Avigad, Azzouni, Gray, O’Halloran, Piantadosi, Ross, Sinclair). On the one hand, mathematics itself seems to be something like a language; Ross discusses the view that mathematics is a universal or ideal language. On the other hand, a question like “Do mathematical objects exist?” is itself a linguistic expression; and it can be argued that difficulties of answering it derive from illusions about the precision or scope of language. Sinclair argues that we may be using the wrong language for mathematics; rather than thinking of mathematical entities as nouns, we should be thinking of them as verbs. Martin and Pease’s essay focuses on the related issue of communication in mathematical collaboration.
· The mathematics of the 21st century (Avigad, Bailey & Borwein, Martin & Pease, Sinclair). Several of our authors look forward to a broadening of the conceptualization and the practice of mathematics in the coming century. The answers to the questions “What is mathematics?” and “What are mathematical objects?” may change, in directions that have recently emerged in the mathematical community.
· Applications. E. Davis considers the applications of geometry to robotics. Bailey and Borwein discuss numerous applications of mathematical simulation including space travel, planetary dynamics, protein analysis, and snow crystals. Verran considers the (mis)applications of statistics to policy. In the opposite direction, Berlinski discusses the difficulty of making precise the sense in which mathematics can be applied at all to physics or to any other non-mathematical domain.
· Psychology: How people think about mathematics. This is front and center in Rips, but it is just below the surface in all the essays. Arguably, that is the real subject of this book.
Why a multidisciplinary2 collection?
In the last few decades, universities, research institutions, and funding agencies have made a large, deliberate effort to encourage interdisciplinary research. There is a good reason for this. On the one hand, there is much important research that requires the involvement of multiple disciplines. On the other hand, overwhelmingly, the institutions of science and scholarship—departments, academic programs, journals, conferences, and so on—are set up along disciplinary lines. As a result, it can often be hard for good interdisciplinary work to get published; for researchers to get promoted, tenured, and recognized; and for students to get trained. Therefore, it is both necessary and highly important for the powers that be to counteract this tendency by energetically welcoming and promoting interdisciplinary research.
However this laudadable effort has often been both taken too far and trivialized. The word “multidisciplinary” and its many near synonyms3 have often become mindless mantras, particularly among university administrators. At times they have become terms of purely generic praise, indiscriminately applied to any research, however, narrow in scope. There has been some healthy reaction against this (e.g., [2]), but in general, the fad is still in full swing.
Since this academic trend is both so important and also so faddish and so often overhyped, it is wise to be initially both welcoming and skeptical of each new manifestation. A collection like this one raises two natural question in that regard. First: The existence of mathematical objects and the truth of mathematical statements are clearly within the purview of the philosophy of mathematics. In fact, they are central questions in the philosophy of mathematics, and there is a large philosophical literature on the subject. So why should one suppose that other disciplines have anything to contribute to the question?
Second: Each of the authors in this collection is an expert in their own discipline, and primarily publishes their work in journal articles and books addressed to other experts in their discipline. Jody Azzouni publishes articles addressed to philosophers in Synthese, Philosophia Mathematica, etc.; Lance Rips and Steve Piantadosi publish articles addressed to psychologists in Psychological Science, Cognition, etc.; and so on down the line. Contrary to the cult of interdisciplinarity, this kind of specialized communication to a limited audience is not regrettable; it is fruitful and essentially inevitable, given the degree of expertise needed to read an original technical research article in any given field. What do we actually expect to accomplish by putting all these disparate viewpoints together between the covers of a book? Will the result be anything more than nineteen specialists all talking past one another?
The essays in this book are themselves the best answer to the first question. Manifestly, each of the disciplines represented here does have its own distinctive viewpoints and approaches to the nature of mathematical objects, mathematical truths, and mathematical knowledge, and brings to bear considerations that the other disciplines tend to discount or overlook. The relations between large cardinal theory and real analysis that John Stillwell explains certainly bear on questions of mathematical ontology; so, in a different way, does the psychological evidence that Lance Rips discusses. I will not say that the question of the nature of mathematics is too important to be left to the philosophers of mathematics; but it is, perhaps, too protean and too elusive.
As regards the second question, one has to keep ones expectations modest, at least in the short term. We do not expect any dramatic direct interdisciplinary cross-fertilizations to emerge here. Lance Rips will not find that David Bailey and Jon Borwein’s computational verification of intricate identities in real analysis give him the key he needs for his studies of the cognitive development of mathematical understanding; nor vice versa. The most that one hopes for is a slight broadening of view, a partial wakening from dogmatic slumbers. As a scientist spends years struggling to apply her own favorite methods to her own chosen problems, it can be easy to lose sight of the fact that there are not only other answers, but even other questions. Seeing the very different way in which other people look at your subject matter is valuable, even though their answers or their questions are only occasionally directly useful, because they shine an indirect light that leads you to your own alternative paths.
Further in the future, though, perhaps we can look forward to a deeper integration of these points of view. In particular, as mentioned above, all of these essays engage with the question of how people think about mathematics; and therefore it is reasonable to suppose that a complete theory of that would explain how people think about mathematics, from basic counting to inaccessible cardinals and beyond, might draw on and combine all these kinds of considerations. This collection is perhaps a small step toward that ultimate overarching vision.
Gaps
There are some regrettable gaps in our collection. On the mathematical side: There is no discussion of probability, which, it seems to me, raises important and difficult questions at least of interpretation, if not of ontology. Verran’s chapter deals incisively with the uses of statistics, but we have no discussion of the theory or the history of statistics. We are thin in algebra; Gray’s and Lützen’s essays discuss 18th and 19th century developments, but the great accomplishments of the 20th century go almost unmentioned; we have no one to tell us in what sense the monster group exists. On the disciplinary side: we have no one from the natural sciences and no one from the arts. It is not so easy to collect all the contributors for a book that one might wish for.
Web site
There is a web site for the book at http://www.cs.nyu.edu/faculty/davise/MathOntology/ with supplementary materials.
Order of chapters
The chapters have been ordered so as to maximize the mean similarity between consecutive chapters, subject to the constraint that the chapter by Martin and Pease came first, since that seemed like a good starting point. Details can be found at the web site.
Excitements
In the final analysis, perhaps the best claim that mathematical objects have on existence is the excitement that they provoke in their devotees. Of all the wonderful material in this book, perhaps my favorite is a short anecdote that Bailey and Borwein tell of Paul Erdős (a variant on steroids of the well-known story of Ramanujan and cab #1729.)
Shortly before his death, Paul Erdős was shown the form
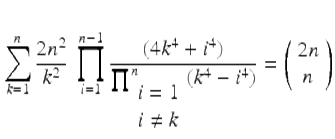
at a meeting in Kalamazoo. He was ill and lethargic, but he immediately perked up, rushed off, and returned 20 minutes later saying excitedly that he had no idea how to prove [the formula], but that if proven it would have implications for the irrationality of ζ(3) and ζ(7). (Somehow in 20 minutes, an unwell Erdős had intuited backwards our whole discovery process.)
Similarly, the best justification for raising the question, “Do mathematical objects exist?” is this collection of fascinating and insightful responses that the question has elicited; even among those authors who have rejected the question as meaningless. Speaking personally, few things in my professional life have given me more pleasure than editing this book with my father.4 It was really thrilling to open each email with a new chapter from another author, and see the wonderful stone soups that they had concocted starting with our simple-minded question. If our readers share that pleasure and excitement, then the book is a success.
Acknowledgements
We thank all the authors for their wonderful contributions and their encouragement. Particular thanks to Jeremy Avigad, Jon Borwein, and Gary Marcus for much helpful feedback and many valuable suggestions.
References
1.
M. Dummett, ‘Truth’, Proceedings of the Aristotelian Society, n.s. 69, 1959, 141–162.
2.
J.A. Jacobs, In defense of disciplines: Interdisciplinarity and specialization in the research university, U. Chicago, 2013.
Footnotes
1
The forthcoming book Weapons of Math Destruction by Cathy O’Neil studies how modern methods of data collection and analysis can feed this kind of abuse.
2
This book is, strictly speaking, multidisplinary rather than interdisciplinary. That is, it brings together multiple disciplines in a single volume, but does not reflect any very strong integration of these.
3
These include “cross-disciplinary,” “extradisciplinary,” “hyperdisciplinary,” “interdisciplinary,” “metadisciplinary,” “neo-disciplinary,” “omnidisciplinary,” “pandisciplinary,” “pluridisciplinary,” “polydisciplinary,” “postdisciplinary,” “supradisciplinary,” “superdisciplinary,” and “transdisciplinary.” The reader may Google for specific citations.
4
Philip Davis and Ernest Davis are father and son, in case you were wondering.