Mathematics, Substance and Surmise: Views on the Meaning and Ontology of Mathematics (2015)
Hardy, Littlewood and polymath
Ursula Martin1 and Alison Pease2
(1)
Department of Computer Science, University of Oxford, Wolfson Building, Parks Road, Oxford, OX1 3QD, UK
(2)
School of Computing, University of Dundee, Queen Mother Building, Balfour Street, Dundee, DD1 4HN, Scotland, UK
Ursula Martin (Corresponding author)
Email: ursula.martin@cs.ox.ac.uk
Alison Pease
Email: a.pease@dundee.ac.uk
Abstract
In the early twenty-first century the polymath experiments saw some of the most distinguished mathematicians in the world work together on significant research problems, writing down what they were doing on a blog for all to see as they went along. They drew widespread attention as they offered an unusual opportunity to see mathematics in progress. In this paper we contrast polymath with a famous collaboration from the early twentieth century, that of the Cambridge mathematicians G H Hardy and J E Littlewood. We look at the collaborations, and the institutions and structures that enabled them, as a contribution to understanding how collaboration enables mathematical advance.
In the early twenty-first century the polymath experiments saw some of the most distinguished mathematicians in the world work together on significant research problems, writing down what they were doing on a blog for all to see as they went along. They drew widespread attention as they offered an unusual opportunity to see mathematics in progress. In this paper we contrast polymath with a famous collaboration from the early twentieth century, that of the Cambridge mathematicians G H Hardy and J E Littlewood. We look at the collaborations, and the institutions and structures that enabled them, as a contribution to understanding how collaboration enables mathematical advance.
1 Hardy and Littlewood
Godfrey Harold Hardy (1877–1947) and John Edensor Littlewood (1885–1977) established the UK as a leading centre of mathematical analysis. Between 1912 and 1948 they published nearly 100 joint papers in analysis and number theory: Hardy published around 300 altogether and Littlewood about half that number.
They had a formidable reputation for joint work, which was less usual at the time than today. Harald Bohr remarked “Nowadays, there are only three really great English mathematicians: Hardy, Littlewood, and Hardy-Littlewood”, and the eminent number theorist Landau wrote “The mathematician Hardy-Littlewood was the best in the world, with Littlewood the more original genius and Hardy the better journalist.”
Their contribution to UK mathematics went well beyond joint papers, taking the UK from something of a backwater of mathematical research to a leading position in the rapidly developing fields of analysis, number theory and the theory of functions.
Both were undergraduates at Cambridge, where mathematical education at the time consisted of coaching for the Tripos, highly competitive and narrow university examinations, with the goal of finishing top of the class and being celebrated as “Senior Wrangler”.
Hardy’s approach to mathematics was transformed by reading Jordan’s “Cours d’analyse”, which he said opened his eyes to “what mathematics really meant”, and through his writing and teaching he brought to the UK the rigour of proof-oriented continental mathematics in the style of Borel, Lebesgue and Landau. His 1908 textbook ‘Pure Mathematics’ was the first exposition in English of analysis in this style: it is renowned for its clarity, and remains in print to this day.
Both helped many students develop successful mathematical careers. Titchmarsh describes “conversation classes” where “Mathematicians of all nationalities and ages were encouraged to hold forth on their own work, and the whole thing was conducted with a delightful informality that gave ample scope for free discussion after each paper”. They navigated the politics to find their proteges positions in Cambridge (the most prized of which, only open to men, were in their own college, Trinity) and elsewhere, and, for the most successful, Fellowships of the Royal Society. Hardy in particular put considerable time into the London Mathematical Society. Since its founding in 1865, it had become the UK’s learned society for mathematics, with its membership reflecting a shift in mathematics research, as a largely amateur community was replaced by mathematicians employed in universities. It had developed an international role in exchange of mathematical ideas, with its journals, famous for their rigorous standards of refereeing, exchanged with mathematical societies around the world, and its monthly meetings in London providing an opportunity for face-to-face discussions. Hardy was president twice; Littlewood claimed as president to have never said anything other than ‘I declare this meeting closed’. Hardy was also active in the International Congress of Mathematicians, and to opening up communication and organising visits to and from overseas mathematicians, in contrast to the isolation of British mathematics in the previous century.
To look back at this collaboration is to look back at a bygone age of gentlemanly politeness, board and lodging and after-dinner conversation in the splendid surroundings of Trinity College, handwritten letters and notes delivered by a college servant, or sent by ship across the world, and apparently abundant free time for watching cricket in Cambridge, or mountaineering during the lengthy vacations.
Hardy saw proof as a collaborative act of understanding, a teacher transmitting a route map to a student. Writing in the philosophy journal Mind in 1929 he responds to contemporary debates on logic and foundation:
I have myself always thought of a mathematician as in the first instance an observer, a man who gazes at a distant range of mountains and notes down his observations. His object is simply to distinguish clearly and notify to others as many different peaks as he can. There are some peaks which he can distinguish easily, while others are less clear. He sees A sharply, while of B he can obtain only transitory glimpses. At last he makes out a ridge which leads from A, and following it to its end he discovers that it culminates in B. B is now fixed in his vision, and from this point he can proceed to further discoveries. In other cases perhaps he can distinguish a ridge which vanishes in the distance, and conjectures that it leads to a peak in the clouds or below the horizon. But when he sees a peak he believes that it is there simply because he sees it. If he wishes someone else to see it, he points to it, either directly or through the chain of summits which led him to recognise it himself. When his pupil also sees it, the research, the argument, the proof is finished.1
The analogy is a rough one, but I am sure that it is not altogether misleading. If we were to push it to its extreme we should be led to a rather paradoxical conclusion; that there is, strictly, no such thing as mathematical proof; that we can, in the last analysis, do nothing but point; that proofs are what Littlewood and I call gas, rhetorical flourishes designed to affect psychology, pictures on the board in the lecture, devices to stimulate the imagination of pupils. This is plainly not the whole truth, but there is a good deal in it. The image gives us a genuine approximation to the processes of mathematical pedagogy on the one hand and of mathematical discovery on the other; it is only the very unsophisticated outsider who imagines that mathematicians make discoveries by turning the handle of some miraculous machine.
Hardy’s Mathematician’s Apology, published in 1940, is a sombre essay on the beauty and purpose of mathematics—emphasising its nature as “A map or picture, the joint product of many hands, a partial and imperfect copy (yet exact so far as it extends) of a section of mathematical reality”. He describes his collaborations with Littlewood and Ramanujan.
All my best work since then has been bound up with theirs, and it is obvious that my association with them was the decisive event of my life. I still say to myself when I am depressed, and find myself forced to listen to pompous and tiresome people, ‘Well, I have done one the thing you could never have done, and that is to have collaborated with both Littlewood and Ramanujan on something like equal terms.’
Littlewood’s Mathematician’s Miscellany is a somewhat more light-hearted collection of reflections—he asserts “A good mathematical joke is better, and better mathematics, than a dozen mediocre papers.” He describes their collaborative process in some detail
[Hardy] took a sensual pleasure in ‘calligraphy’, and it would have been a deprivation if he didn’t make the final copy of a joint paper. (My standard role in a joint paper was to make the logical skeleton, in shorthand - no distinction between r and r 2, 2π and 1, etc., etc. But when I said ‘Lemma 17’ it stayed Lemma 17.)
and elsewhere describing how Hardy unabbreviated the shorthand and added “what we used to call ‘gas’.” Hardy’s deprivation was perhaps not all Littlewood claimed—as Hardy wrote to Bertrand Russell in 1919
I wish you could find some tactful way of stirring up Littlewood to do a little writing. Heavens knows I am conscious of my huge debt to him. But the situation which is gradually stereotyping itself is very trying for me. It is that, in our collaboration, he will contribute ideas and ideas only: and that all the tedious part of the work has to be done by me. If I don’t, it simply isn’t done, and nothing would ever get published.
Dame Mary Cartwright (1900–1998) was a former student of Hardy and collaborator of both, the first female FRS in mathematics, and subsequently Mistress of Girton College Cambridge2. In a series of papers written when she was over 80 she drew upon Cambridge’s archives of Hardy’s and Littlewood’s manuscripts, and her own memories and notes, to analyse their collaboration. Much of this was by letter: although their rooms in Trinity College were only a few minutes apart, they would often communicate through notes delivered by a servant. They were frequently in different places—from 1915–1919 Littlewood was away on war service; from 1920 to 1931 Hardy worked in Oxford; and in any case outside the short Cambridge terms (24 weeks a year in all) both travelled extensively, whether to work with overseas mathematicians or on lengthy holidays. According to Cartwright they rarely, if ever sat down together to write mathematics, and never discussed at a blackboard, though they did talk to each frequently to discuss critical points and to establish notation, which Littlewood disliked changing as he did a great deal of work in his head. Littlewood, who seems rarely to have bought paper and used all sorts of scraps, including the backs of exam papers and committee minutes, would write terse notes. Hardy, who prided himself on his hand-writing, and bought high-quality new paper (though he was careful to use both sides) would write out a draft and return it to Littlewood alongside the original for Littlewood to check. This way of working sometime led to confusion as when Hardy writes “Also return the scrap of your writing, since otherwise I shall have a letter of yours, not yet exhausted, with a mysterious hole in the middle and shall be confused when I have forgotten what it contained. I have various MSS of yours with irritating holes of this kind in them, and am always wondering if the hole didn’t contain just the point.”
A typical collaboration was on the paper, “A maximal theorem with function theoretic applications”, which appeared in Acta Mathematica in July 1930. The main results are motivated by a maximisation theorem explained in a footnote: “The arguments used …are indeed mostly of the type which are intuitive to a student of cricket averages. A batsman’s average is increased by his playing an innings greater than his present average; if his average is increased by playing an innings x, it is further increased by playing next an innings y > x; and so forth”. The 36 pages of the paper contain 27 theorems, and thanks to the clear exposition (or copious amounts of “gas”) is still very readable: all the proofs are clearly set out, with plenty of surrounding text to motivate them, explain why results are best possible and other possible generalisations and proof techniques will not work, and so on.
The published papers reflect Hardy and Littlewood’s correspondence, as they discuss hypotheses, difficulties, and alternative ways of arranging and synthesising material, or postponing some of it to future papers or collaborations with others. Ideas pass back and forth with requests from one or the other to give their opinion on a proposed piece of work or to “Please check” drafts. Both seem at ease asking for help or acknowledging mistakes: for example, Hardy writes “Over this I have, at various times, spent many fruitless hours. I seem to remember your saying that you once thought you had it, but succeeded in evading it. If so, you must app ly have been at one time (what I never have) in apparent possession of adequate ideas & I wish you’d tell me roughly how you were arguing” or elsewhere “Here’s the hell of a mess: it seems that the proofs …are just fallacious” and “But I have the feeling that I must have missed something more obvious” or even “Are we not both being asses…”. In an echo of the philosophical issues in the 1929 Mind paper Hardy distinguishes between ‘checking’ and ‘understanding’, writing of one of Littlewood’s drafts that “It is a masterpiece of ingenuity, but very difficult (to “understand”, not to check.)”
Bohr’s 1947 article summarised what he called Hardy and Littlewood’s Axioms of Collaboration, presented by Cartwright as:
1.
When one wrote to the other, it was completely indifferent whether what they wrote was right or wrong.
2.
When one received a letter from the other, he was under no obligation to read it, let alone answer it.
3.
Although it did not really matter if they both simultaneously thought about the same detail, still it was preferable that they should not do so.
4.
It was quite indifferent if one of them had not contributed the least bit to the contents of a paper under their common name.
While she is in agreement with their overall tone, Cartwright’s analysis suggests that the Axioms themselves, and parts of the ‘Mathematicians Apology’, were somewhat rhetorical and at odds with the evidence of the letters, and the kindness of both men to students and collaborators: she suggests the word “indifferent” perhaps should be read as something akin to “tolerant of”. She reported that in her own collaborations, Littlewood “would not let me put his name to any paper not actually written by him. I had to say it was based on joint work with him”. Unusually for senior scientists of the time, Hardy and Littlewood seem to be have been generous with crediting the contributions of their students in their papers, either through footnotes or through naming them as co-authors.
In 1913 Hardy responded to a letter from the unknown Indian mathematician, Ramanujan, who had previously written to several of Hardy’s more senior colleagues without getting a reply. This led to Ramanujan coming to Cambridge, and another remarkable collaboration, and five joint papers, earning Ramanujan an FRS and subsequently a fellowship of Trinity College (though the college’s inability to provide his vegetarian diet meant he ate alone in his rooms). Ramanujan had an extraordinary mathematical intuition and was able to perceive remarkable combinatorial identities and asymptotic results. Working with Hardy he learned contemporary standards of exposition and proof, which he had not previously encountered. Hardy’s mastery of European analytic function theory coupled with Ramaunjan’s insight was, to quote Littlewood, “a singularly happy collaboration of two men, of quite unlike gifts, in which each contributed the best, most characteristic, and most fortunate work that was in him”.
A profound result providing an exact formula for p(n), the number of partitions of an integer, was also remarkable for the contribution of Percy McMahon. A former soldier and an instructor at a military college, McMahon wrote on combinatory analysis in the older tradition of English mathematics, and was famous for his calculating ability. Hardy and Ramanujan sought his help in calculating the first 200 values of p(n), and as they acknowledge in the paper:
To Major MacMahon in particular we owe many thanks for the amount of trouble he has taken over very tedious calculations. It is certain that, without the encouragement given by the results of these calculations, we should never have attempted to prove theoretical results at all comparable in precision with those which we have enunciated.
2 polymath
Timothy Gowers, a successor to Littlewood in the Rouse Ball chair at Cambridge, was awarded a Fields Medal in 1998 for work combining functional analysis and combinatorics, in particular his proof of Szemerdi’s theorem. Gowers has characterised himself as a problem-solver rather than a theory-builder, drawing attention to the importance of problem solvers and problem solving in understanding and developing broad connections and analogies between topics not yet amenable to precise unifying theories. He writes articulately on his blog about many topics connected with mathematics, education and open science, and used this forum to launch his experiments in online collaborative proof which he called “polymath”.
In a blog post on 27th January 2009 he asked “Is massively collaborative mathematics possible”, suggesting that “If a large group of mathematicians could connect their brains efficiently, they could perhaps solve problems very efficiently as well”, and proposing some ground rules, which we reproduce in an appendix. The post attracted 203 comments from around the globe, exploring philosophical and practical aspects of working together on a blog to solve problems, and a few days later he launched the first experiment. The problem chosen was to find a new proof of the density version of the “Hales Jewett Theorem”, replacing the previously known very technical proof with a more accessible combinatorial argument which, it was hoped, would also open the door to generalisations of the result. Over the next seven weeks, 27 people contributed around 800 comments—around 170,000 words in all—with the contributors ranging from high-school teacher Jason Dyer to Gowers’s fellow Fields Medallist Terry Tao. On March 10, 2009 Gowers was able to announce a new combinatorial proof of the result, writing “If this were a conventional way of producing mathematics, then it would be premature to make such an announcement—one would wait until the proof was completely written up with every single i dotted and every t crossed—but this is blog maths and we’re free to make up conventions as we go along”.
The result was written up as a conventional journal paper, with the author given as “D H J Polymath”—identifying the actual contributors requires some detective work on the blog—and published on the arxiv in 2009, and in the Annals of Mathematics in 2012. The journal version explains the process
Before we start working towards the proof of the theorem, we would like briefly to mention that it was proved in a rather unusual “open source” way, which is why it is being published under a pseudonym. The work was carried out by several researchers, who wrote their thoughts, as they had them, in the form of blog comments at http://gowers.wordpress.com. Anybody who wanted to could participate, and at all stages of the process the comments were fully open to anybody who was interested.”
A typical extract from the blog (Figure 1) shows the style of interaction. Participants, in line with the ground rules, were encouraged to present their ideas in an accessible way, to put forward partial ideas that might be wrong—“better to have had five stupid ideas than no ideas at all”, to test out ideas on other participants before doing substantial work on them, and to treat other participants with respect. As the volume of comments and ideas grew, it became apparent that the blog structure made it hard for readers to extract the thread of the argument and keep up with what was going on, without having to digest everything that had been previously posted, and in future experiments a leader took on the task of drawing together the threads from time to time, identifying the most appropriate next direction, and restarting the discussion with a substantial new blog post.
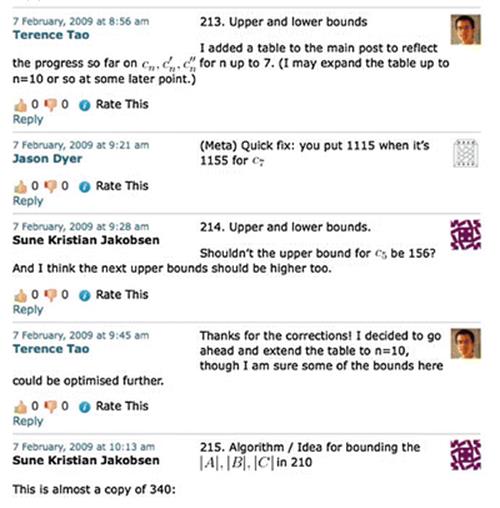
Fig. 1
An extract from the polymath blog for the proof of the Density Hales Jewett theorem
By 2015 there had been nine endeavours in the polymath sequence, and a number of others in similar style. Not all had achieved publishable results, with some petering out through lack of participation, but all have left the record of their partial achievements online for others to see and learn from—a marked contrast to partial proof attempts that would normally end up in a waste-basket. The minipolymath series applied the polymath model to problems drawn from the International Mathematics Olympiad, in an attempt to learn more about the approach—problems typically took hours rather than months to be solved—and the accessible nature of the problem allowed a much greater range of participants.
polymath 8, launched in the summer of 2013, was motivated by Yitang Zhang’s proof of a result about bounded gaps between primes. The twin primes conjecture states that there are infinitely many pairs of primes that differ by 2: for example 3, 5; 11; 13 and so on. Zhang proved that there is a number K such that infinitely many pairs of primes differ by at most K, and showed that K is less than 70,000,000. After various discussions on other blogs, Tao formally launched the project, to improve the bound on K, on 13th June 2013. The first part of the project, polymath 8a, concluded with a bound of 4,680, and a research paper, also put together collaboratively, appeared on the arxiv in February 2014. The second part, polymath 8b, combined this with techniques independently developed in parallel by James Maynard, to reach a bound of 246, with a research paper appearing on the arxiv in July 2014. The participants also used Tao’s blog to seek input for a retrospective paper reflecting on the experience, which appeared in the arxiv in September 2014.
One immediate concern was the scoping of the enquiry so as not to intimidate or hamper individuals working on their own on this hot topic: it was felt that this was more than countered by providing a resource for the mathematical community that would capture progress, and provide a way to pull together what would otherwise be many independent tweaks. The work was well suited to the polymath approach: the combination of Tao’s leadership and the timeliness of the problem made it easy to recruit participants; the bound provided an obvious metric of progress and maintained momentum; and it naturally fell into five components forming what Tao called a “factory production line”. The collaborative approach allowed people to learn new material, and brought rapid sharing of expertise, in particular knowledge of the literature, and access to computational and software skills.
Tao himself explained how he was drawn into the project, even though it interrupted another big project a piece of work that he expects to take some years, by the ease of making simple improvements to Zhang’s bound, and summed up by saying “All in all, it was an exhausting and unpredictable experience, but also a highly thrilling and rewarding one.” The time commitment was indeed intense—for example, a typical thread “polymath8b, II: Optimising the variational problem and the sieve” started on 22 November 2013, and ran for just over two weeks until 8th December. The initial post by Tao runs to about 4000 words—it is followed by 129 posts, of which 36, or just under a third, are also by Tao.
Tao and other participants were motivated above all by the kudos of solving a high-profile problem, in a way that was unlikely had they worked individually, but also by the excitement of the project, and the enthusiasm of the participants and the wider community. They reported enjoying working in this new way, especially the opportunity to work alongside research stars, the friendliness of the other participants, and their tolerance of errors, and the way in which the problem itself and the polymath format provided the incentive of frequent incremental progress, in a way not typical of solo working.
Participants needed to balance the incentives for participation against other concerns. Chief among these was the time commitment: participants reported the need for intense concentration and focus, with some working on it at a “furious pace” for several months; some feeling that the time required to grasp everything that was happening on the blog make polymath collaborations more, rather than less, time consuming than traditional individual work or small-group collaboration; and some feeling that the fast pace was deterring participants whose working style was slower and more reflective.
Pure mathematicians typically produce one or two journal papers a year, so, particularly for those who do not yet have established positions, there will be concerns that a substantial investment of time in polymath might damage their publication record. While such a time commitment would normally be worth the risk for a high-profile problem that has the likely reward of a good publication, the benefits are less clear-cut when the paper is authored under a group pseudonym (D H J Polymath), with the list of participants given in a linked wiki. As a participant remarked “polymath was a risk for those who did not have tenure”. On the other hand, in a fast moving area, participants may feel that incorporating their ideas into the collective allows them to make a contribution that they would not have achieved with solo work, or that engaging in this way is better than being beaten to a result and getting no credit, especially if participation in a widely read blog is already adding to their external reputation.
An additional risk for those worried about their reputation can be that mistakes are exposed for ever in a public forum: pre-tenure mathematician Pace Nielsen was surprised that people were “impressed with my bravery” and would advise considering this issue before taking part. Rising star James Maynard observed: “It was very unusual for me to work in such a large group and so publicly—one really needed to lose inhibitions and be willing to post ideas that were not fully formed (and potentially wrong!) online for everyone to see.”
Those reading the polymath 8 sites went well beyond the experts—with an audience appreciating the chance to see how mathematics was done behind the scenes, or as Tao put it “How the sausage is made”. At its height it was getting three thousand hits a day, and even readers who knew little mathematics reported the excitement of checking regularly and watching the bounds go down. All the members of a class of number theory students at a summer school on Bounded Gaps admitted to following polymath. Perhaps typical was Andrew Roberts, an undergraduate who thanked the organisers for such an educational resource and reported “reading the posts and following the ‘leader-board’ felt a lot like an academic spectator sport. It was surreal, a bit like watching a piece of history as it occurred. It made the mathematics feel much more alive and social, rather than just coming from a textbook. I don’t think us undergrads often get the chance to peak behind closed doors and watch professional mathematicians ‘in the wild’ like this, so from a career standpoint, it was illuminating”. David Roberts, an Australian educator who used polymath in his classes to show students how the things they were learning were being used in cutting-edge research, reported “For me personally it felt like being able to sneak into the garage and watch a high-performance engine being built up from scratch; something I could never do, but could appreciate the end result, and admire the process”. The good manners remarked upon by the expert participants extended to less-well informed users, with questions and comments from non-experts generally getting a polite response, often from Tao himself, and a few more outlandish comments, such as claims of a simple proof, being ignored except for a plethora of down-votes.
The experiments have attracted widespread attention, in academia and beyond. Gowers had worked closely with physicist Michael Nielson in designing the wiki and blog structure to support polymath, and in an article in Nature in 2009 the pair reflected on its wider implications, a theme developed further in Nielsen’s 2012 book, Reinventing Discovery, and picked up by researchers in social and computer science analysing the broader phenomenon of open science enabled by the internet.
Like the participants, the analysts remarked on the value of the polymath blogs for capturing the records of how mathematics is done, the kinds of thinking that goes into the production of a proof, such as experimenting with examples, computations and concepts, and showing the dead ends and blind alleys. As Gowers and Nielson put it, “Who would have guessed that the working record of a mathematical project would read like a thriller?” The working records provide data for online ethnography, allowing analysis of what is involved in the creation of a proof—for example in the minipolymath projects as little as 30% of the comments were actual proof steps, with the rest being analysis of examples, concepts and so on.
Although polymath is often described as “crowdsourced science”, the crowd is a remarkably small and expert one. The analogy has often been drawn with open source software projects—however these are typically organised in a much more modular and top-down fashion than is possible in developing a mathematical proof, where many ideas and strands will be interwoven in a manner, as Nielsen comments, much more akin to a novel.
These studies of crowdsourcing help explain the success of polymath and other attempts at open collaboration in mathematics. Mathematicians have well-established shared standards for exposition and argument, making it easy to resolve disputes. As the proof develops, the blog provides a shared cognitive space and short-term working memory. The ground rules allow for a dynamic division of labour, and encourage a breakdown into smaller subtasks thus reducing barriers to entry and increasing diversity. This diversity of skills is encouraged, and a later stage might be to design some form of rating or ranking—an “attention architecture”—so that participants can more easily find the subtask where they might be able to contribute, and more readily explore past contributions.
A striking aspect of polymath is that senior figures in the field are prepared to try such a bold experiment, to think though clearly for themselves what the requirements are, and to take a “user centred” view of the design. For example, it was suggested that participants might use a platform such as github, designed to support distributed version control, to make the final stage, collaborating on a paper, more straightforward: Tao’s response was to prioritise user accessibility: “One thing I worry about is that if we use any form of technology more complicated than a blog comment box, we might lose some of the participants who might be turned off by the learning curve required”. On the whole polymath has proved successful in solving problems amenable to the approach, with the added benefit of presenting to the public a new way of mathematics. The failures have been through failures to find the necessary mathematical breakthrough, rather than to any obvious failures of the polymath format.
3 Conclusions
To study the practice of mathematics is to study not only the theorems produced, but also what the individuals and institutions involved in their creation do to bring them about. Insofar as mathematical results require readers as well as writers, and mathematical knowledge accretes by building on the work of others, mathematics has always been a collaborative endeavour. To quote David Hume, writing in 1739
There is no Algebraist nor Mathematician so expert in his science, as to place entire confidence in any truth immediately upon his discovery of it, or regard it as any thing, but a mere probability. Every time he runs over his proofs, his confidence encreases; but still more by the approbation of his friends; and is rais’d to its utmost perfection by the universal assent and applauses of the learned world.
The institutions surrounding mathematics provide trusted and well-established mechanisms for accrediting and disseminating knowledge through journals, meetings and opportunities for informal exchange, and rely on the collaboration of mathematicians for their success and authority, complementing the professionalisation of mathematics research and education, through employment of mathematicians by universities. They enable development and transmission of shared concepts and methods: not just the mathematical objects under consideration, but also expectations of rigour, proof and exposition; notions of what constitutes significant research questions; and expectations of how a professional mathematician should conduct themselves—for example in matters of citation or co-authorship.
Cartwright, Hardy, Littlewood, McMahon and Ramanujan collaborated at a time when these mechanisms were becoming fixed, provided through leading mathematics departments in Europe and the USA, and emerging learned societies patterned on the London Mathematical Society. One hundred years later collaborating pure mathematicians, the polymath collaborators included, still have as their ultimate goal research papers that meet traditional refereeing standards and are published in the conventional way. The goals of scholars are still a mixture of intellectual satisfaction and professional recognition, with then, as now, success measured by proving significant results and publishing them in significant journals, or the additional recognition of well-known prizes. A modern-day Cartwright or Ramanujan would take it for granted that men and women could apply for the same jobs, and expect to find something to eat when at work, and have their applications judged on objective criteria—though aware that the added kudos of a letter of reference from a major player or a highly visible online presence could do no harm.
Then, as now, successful collaboration requires a shared understanding of the mathematical objects under consideration, shared notions of rigour, proof and exposition, shared expectations of how professional mathematicians should conduct themselves, and above all that the collaborators have collectively the skills needed to solve the problem.
For modern collaborators the most striking difference is the speed of communication and the quantity and availability of information. Thanks to email, github, latex and skype mathematicians can collaborate at a distance, share hand-written drafts and work together on the final version of documents; blogs and facebook have replaced attendance at monthly meetings of the London Mathematical Society as a means of catching up with the latest scientific gossip; and the calculating skills of McMahon are as redundant as those of the blacksmith. Papers are available immediately they are written through the arxiv, rather than having to wait for them to cross the ocean in printed form and appear on the shelves of a library, and scholars can readily search, find and access current and historical literature. It has been argued that this flattening is providing a homogenising effect that has negative aspects—in that uniform expectations and standards are crowding out the distinctive approaches which might come from individuals who have not been through a standard education system, and further that the decline of distinct schools of mathematics, such as those that flourished in the former Soviet union, is leading to a narrowing not just of techniques and skills, but also of intellectual approach, restricting the kinds of mathematical questions that are asked.
All of this is true of any twenty-first century collaboration. Perhaps what is most remarkable and distinctive about the polymath experiments is the public display and sharing which was not possible in the past. An early aspiration for polymath—that the format would allow contributors to take part in small pieces of the discussion—was not really fulfilled as participants found that the fast pace required intense concentration and focus, and to leave and return was not really possible as it required too much effort to catch up with progress in the interim. However polymath succeeded in opening up the process of mathematical discovery to a wide audience from a variety of backgrounds, and the ground rules, and the involvement of senior figures on the discussions, reinforced in a very open and public way expectations of how mathematical collaboration should be conducted.
A number of participants and possible participants remarked on their distaste for the fast pace of polymath discussions, which requires people to work quickly and not mind making mistakes in public, and wondered whether this is really a necessary condition for collaboration, or merely a way for people who are comfortable with this to gain status in the community. One feels that G H Hardy, who hated the highly competitive nineteenth century Cambridge mathematical tripos, and was well known for his reticence with strangers, would have agreed.
Acknowledgements
The first author acknowledges support from the UK Engineering and Physical Sciences Research Council under grant EP/K040251.
Appendix—the polymath Ground Rules
These ground rules are reproduced from Gowers’s Weblog post of 27 January 2009
1.
The aim will be to produce a proof in a top-down manner. Thus, at least to start with, comments should be short and not too technical: they would be more like feasibility studies of various ideas.
2.
Comments should be as easy to understand as is humanly possible. For a truly collaborative project it is not enough to have a good idea: you have to express it in such a way that others can build on it.
3.
When you do research, you are more likely to succeed if you try out lots of stupid ideas. Similarly, stupid comments are welcome here. (In the sense in which I am using ‘stupid’, it means something completely different from ‘unintelligent’. It just means not fully thought through.)
4.
If you can see why somebody else’s comment is stupid, point it out in a polite way. And if someone points out that your comment is stupid, do not take offence: better to have had five stupid ideas than no ideas at all. And if somebody wrongly points out that your idea is stupid, it is even more important not to take offence: just explain gently why their dismissal of your idea is itself stupid.
5.
Don’t actually use the word ‘stupid’, except perhaps of yourself.
6.
The ideal outcome would be a solution of the problem with no single individual having to think all that hard. The hard thought would be done by a sort of super-mathematician whose brain is distributed amongst bits of the brains of lots of interlinked people. So try to resist the temptation to go away and think about something and come back with carefully polished thoughts: just give quick reactions to what you read and hope that the conversation will develop in good directions.
7.
If you are convinced that you could answer a question, but it would just need a couple of weeks to go away and try a few things out, then still resist the temptation to do that. Instead, explain briefly, but as precisely as you can, why you think it is feasible to answer the question and see if the collective approach gets to the answer more quickly. (The hope is that every big idea can be broken down into a sequence of small ideas. The job of any individual collaborator is to have these small ideas until the big idea becomes obvious and therefore just a small addition to what has gone before.) Only go off on your own if there is a general consensus that is what you should do.
8.
Similarly, suppose that somebody has an imprecise idea and you think that you can write out a fully precise version. This could be extremely valuable to the project, but don‘t rush ahead and do it. First, announce in a comment what you think you can do. If the responses to your comment suggest that others would welcome a fully detailed proof of some substatement, then write a further comment with a fully motivated explanation of what it is you can prove, and give a link to a pdf file that contains the proof.
9.
Actual technical work, as described in 8, will mainly be of use if it can be treated as a module. That is, one would ideally like the result to be a short statement that others can use without understanding its proof.
10.
Keep the discussion focused. For instance, if the project concerns a particular approach to a particular problem (as it will do at first), and it causes you to think of a completely different approach to that problem, or of a possible way of solving a different problem, then by all means mention this, but don’t disappear down a different track.
11.
However, if the different track seems to be particularly fruitful, then it would perhaps be OK to suggest it, and if there is widespread agreement that it would in fact be a good idea to abandon the original project (possibly temporarily) and pursue a new one—a kind of decision that individual mathematicians make all the time—then that is permissible.
12.
Suppose the experiment actually results in something publishable. Even if only a very small number of people contribute the lion’s share of the ideas, the paper will still be submitted under a collective pseudonym with a link to the entire online discussion.
Further reading
Hardy and Littlewood
Mathematical Proof, G H Hardy, Mind 38 (1929), 1–25
A Mathematician’s Apology, G H Hardy, Cambridge University Press 1940
Littlewood’s Miscellany, edited by Bela Bollobas, Cambridge University Press 1986
Some Hardy-Littlewood Manuscripts, M L Cartwright, Bulletin of the London Mathematical Society 13 (1981), 273–300
Later Hardy and Littlewood Manuscripts, M L Cartwright, Bulletin of the London Mathematical Society 17 (1985), 318–390
Partnership and Partition: A Case Study of Mathematical Exchange within the London Mathematical Society, Adrian Rice, Philosophia Scientiae, 19 (2015) 5–24
The polymath initiative
Massively collaborative mathematics, Timothy Gowers and Michael Nielsen, Nature, 461 (2009) 879–881
The polymath Blog http://polymathprojects.org
The polymath wiki http://michaelnielsen.org/polymath1
“Is massively collaborative mathematics possible?”, Gowers’s Weblog, Retrieved 2015-3-16. https://gowers.wordpress.com/2009/01/27/is-massively-collaborative-mathematics-possible/
Reinventing discovery, Michael Nielsen, Princeton 2012
D H J Polymath, “The ‘bounded gaps between primes’ polymath project: A retrospective analysis”, Newsletter of the European Mathematical Society, 94 (2014) 13–23
Footnotes
1
The wording calls to mind Odell’s graphic description of the last sighting of his fellow climbers Mallory and Irvine, both known to Hardy, in their attempt on Everest in 1924: “In the sudden clearing of the atmosphere above me I saw the whole summit ridge and finally the peak of Everest unveiled”.
2
In the mid-twentieth century Cambridge had two women-only colleges and the rest, around two dozen, were all male.