Mathematics, Substance and Surmise: Views on the Meaning and Ontology of Mathematics (2015)
What kind of thing might number become?
Nathalie Sinclair1
(1)
Faculty of Education, Simon Fraser University, 8888 University Drive, Burnaby, BC, Canada, V5A 1S6
Nathalie Sinclair
Email: nathsinc@sfu.ca
Abstract
Inspired by the work of Abraham Seidenberg, on the ritual origins of counting, as well as contemporary philosophical work on the embodied nature of mathematical concepts, this chapter proposes an alternate way of approaching number that places much more emphasis on ordinality, rather than cardinality, and that highlights number's temporality. This conception of number is then shown to be at play in the way young children engage with TouchCounts, an App designed to support early number sense.
This chapter will explore the possibility of number as an event rather than an object; that is, seeing number as temporal. The issue of time is a very delicate one in mathematics, which tends to excel at encapsulating anything that may be temporal (counting, plotting, rotating, etc.) into a timeless, seemingly immutable object (such as number). Indeed, it can be hard to think of mathematical objects such as number, set and point as anything but static, self-contained things. The title of this chapter suggests that we might indeed imagine number otherwise. It plays on the threefold assumptions of the question ‘what kind of thing is number?’, a question often posed by philosophers of mathematics1: one, number is a thing; two, things come in kinds; three, things and kinds of things are timeless (hence the apparent a temporality of ‘is’).
Another assumption of the oft-posed question ‘what kind of thing is number?’ is that number is a singular entity: an alternative phrasing of the title could have been ‘what kinds of things are numbers?’ Indeed, there have been several views, described by historians, philosophers, mathematicians and educators alike, on what a number is (or what numbers are). While some have tried to encapsulate various types of numbers (whole, rational, real, complex, infinitesimal, hyperreal, etc.) into one overarching definition, others have focused on particular numbers.
In this chapter, I will be particularly interested in whole numbers, both for historical reasons and for pedagogical ones. Unlike current everyday uses of the word ‘number’, the early Greek term widely used for number, arithmos, was always a whole number, “and tied up with the actual procedure of counting” [4, p. 265]. Besides the question of whether to opt for the singular or the plural form, one might also question the common use of ‘number’ as a noun. Fowler [10] points out that number can be adverbial as well (as in, she fell twice, where ‘twice’ is a particular adverbial form of the number two).
In addition to being nouns and adverbs, numbers can also function as a verb in the sense that to number is to call into existence or to evoke. In the context of her work with the Mi’kmaw community, whose language (like most indigenous languages in Canada) is verb-based, Lisa Lunney Borden [3] has proposed a re-verbification of mathematics in which nominalisations such as ‘number’ could be infused with process, action and flux, thus moving away from the notion of fixed and rigid separate objects. This chapter can be seen as an initial step in this direction.
To set the stage for my arguments, I briefly outline the thesis proposed by the mathematician and historian of mathematics Abraham Seidenberg [19], on the ritual origins of counting. His thesis will set the stage for an alternate way of approaching the historical aspect of how number becomes, and will serve to highlight the temporal (and perhaps even rhythmic) nature of number. I then consider my chapter title question from the perspective of young children engaged with a multi-touch audio-visuo-tangible digital environment for counting, adding and subtracting called TouchCounts. My goal is not to argue for its pedagogical effectiveness but, rather, to show how the children’s experiences offer new possibilities for what number can be and, as a consequence, how it might be learned, while also to echo strongly with Seidenberg’s sense of the ritual origin of counting. Finally, I draw on ideas in contemporary philosophy that provide new ways of thinking about what number is and might be, in terms of both its logical and its epistemological nature. The main advantage of these ideas is that they provide some explanatory tools for understanding how the physical (which is usually recognised as being temporal) and the mathematical (usually not) can be related, and how mathematical concepts can emerge from human actions in the world.
1 “But how can one ask ‘How many?’ until one knows how to count?”
Primary school mathematics in many countries around the world, including Canada and the United States, take the question “How many?” as the driving force of the curriculum related to number. Children are routinely asked to say how many blocks or cookies or people there are in a given collection, and they usually do so by engaging the ritual of sequential counting, which involves pointing at or touching the objects while also saying a sequence of number words in a language. Children are also asked to compare numbers, but using the cardinal approach of having to decide which is greater or which is smaller, rather than which comes after which or which comes first in the spoken word sequence.
For small sets, young children are increasingly encouraged to use subitising to answer the question. Subitising (from the Latin word subitus, which means sudden), involves enumerating without counting, usually through visual perception (subitising 5 when the objects are configured as on a die can be much easier than for random configurations—see Figure 1). Subitising is valued in schools because it involves a cardinal conception of number, which in turn enables children to perform addition tasks like 5 + 3 more easily since they can “add on” 3 to the 5 instead of counting out five and then counting three more.
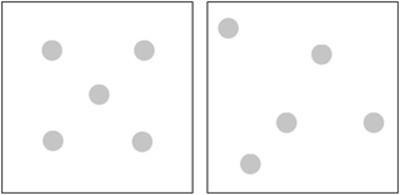
Figure 1
The circles on the left are easier to subitise than those on the right
The emphasis on cardinal forms of comparison goes back at least to the work of the Swiss developmental psychologist Jean Piaget, who focused on children’s ability to discriminate among arrays of objects on the basis of the quantity of them present. The focus on quantity can also be seen in Gelman and Gallistel’s [12] five principles of counting, which have been highly influential in mathematics education research. These are: (1) the importance of assigning only one counting tag to each counted object in the array (the principle of one-to-one correspondence); (2) number words should be provided in a constant order when counting; (3) repeated counting of the same set must always produce the same final number word (often called the cardinality principle; it presupposes (1) and (2)); (4) it does not matter whether the items in the set are identical; and (5) it does not matter in which order objects are counted. The first three deal with how to count, where the objective of counting is clearly to answer the “how many?” question. Indeed, the third “principle of counting” is itself the cardinality principle, namely that repeated counting of the same set must always provide the same final number. In other words, counting is seen as being aimed towards the saying of the final number word. More recently, neuroscientists have also focused on cardinality as being core to human (and, indeed, animal) number sense (e.g., Neider & Dehaene [16]).
In the rush towards cardinality, then, what it means to be a number in primary school mathematics is very clearly about quantity. Depending on your interests and expertise, this may seem totally natural. (But like most aesthetic and perhaps even political choices, what is natural is largely a matter of enculturation.) But I would like to argue that there is much more to mean by a number—especially in terms of ordinality. Indeed, the philosopher Alain Badiou [1] has insisted, drawing on the work of mathematicians Richard Dedekind and Georg Cantor, that “ordinals constitute the absolute ontological horizon of all numbers” (p. 68). For Dedekind, number was to be thought of as a link in a chain; it was about sequence, or seriation. For Cantor, number was also about seriation, but his focus is on order (and the well-ordering principle for which the natural numbers provide an excellent model as well as a source of intuition). The latter describes the way in which: (1) given two numbers, one will always come after the other; (2) given a set of numbers, there will always be one that came first. Neither of these have anything, a priori, to do with answering “how many?”. They may be thought of as tools that enable one to answer the “how many?” question, but might they also be tools for accomplishing something else? As with most tools, they take time to apply: ordinals are produced over time and questions about order are decided in time.
In discussing Cantor’s work, Badiou [1] describes order in terms of which number will be greater and in terms of which number will be smaller. This may be evidence of some slippage into cardinality, which seems hard to avoid. My own re-wording into a temporal register is inspired by the work of Seidenberg, which can be helpful in reclaiming ordinality. The title of this section is taken from Seidenberg’s paper [19]. It is relevant both to pedagogy and to mathematics. In terms of the latter, as Seidenberg notes, modern theories put forth by the logicians Gottlob Frege and Bertrand Russell analyse the concept of number without much attention to ordinality. They speak of “how many?” with little attention to counting. But theirs is a paradigmatic de-temporalisation of number, and it has found its way into the pedagogical realm.
In contrast to Dedekind and Cantor, who were developing mathematical theories of number, Seidenberg was interested in the origins of number and, in particular, the origins of counting. As he writes, most historical accounts of number trace its spread across cultures. But Seidenberg aimed to identify the special circumstance of its origin, which he argued cannot be indicated by its use or by its practical applications: “an application of a device (or idea) is an effect of the device, not a cause” (p. 2). He proposes a ritual origin for counting, one that speaks significantly of myths and rites. He draws on the work of Lord Raglan [17], who connects them thus: a myth “is a narrative linked with a rite” (p. 117), where a rite is the corresponding enacted practice. Taking these ideas of myth and rite into the specific context of numbering, Seidenberg observes, “the ‘serializing’ is the rite, and the ‘counting’ is the myth” (p. 10).
Based on extensive anthropological evidence, Seidenberg’s contention is that the origin of counting lies in a creation ritual, in the bringing onto stage the correct deities in the correct order. These techniques, according to Seidenberg’s account, were later adapted to counting and geometrical measurement. (There is also evidence that this creation ritual involved counting by 2s, much as in Noah’s ark, which would mean that counting on one’s fingers—either by 5s or 10s—is a later development, with hand gestures sometimes used to count silently under speaking taboos.) Thus, counting emerges first by associating number names with deities, which means that numbers did not exist prior to their ritual application. One might more appropriately speak of numbering as a verb, rather than number. The names of participants in the ritual, or the words announcing them, were the original number words. This ritual suffuses itself into all sorts of activities. Seidenberg again:
The original intention is to mimic a portion of the Creation ritual. It is in this way that we envisage “counting” to have become detached from the ritual and to have acquired its abstract or general character. Higher counting may have started as a method of taking care of longer and longer processions (not with the idea of counting them, however). The base (which is not logically inherent in counting) corresponds to the number of persons in the basic ritual, and the higher counting derives from the continued repetition, with slight modifications, of this basic ritual. (p. 10)
The child who puts her stuffed animals one by one on a table, naming each one as it is placed there (with its proper name, of course, and not as ‘elephant’ or ‘dog’), is thus involved in the rite of counting. These stuffed animals are ordered by time, and not by name. Her myth (the names of the stuffed animals) does not correspond with current English number myths, but that is a mere detail. In this counting, the question of how many stuffed animals are on the table is of little concern. However, the first one there will likely have meaning, and the difference between the third and the fifth ones too, in terms of the order in which they appeared, not in terms of the quantity of stuffed animals thus far named. I note that while it is customary to think of the counting myth in terms of named numbers (‘three’ or ‘eight’), we can also think of them in their symbolic form (‘3’ or ‘8’). The child who writes a series of marks on the paper, 1 2 3 4, etc., can thus also be seen as participating in a creation ritual. No sense of quantity is required—no more, at least, than what might be required to be able to write a b c.
I am not arguing here that ontogeny recapitulates phylogeny; I am not making a developmental argument. I am simply pointing to some of the distinctive features of number that this counting myth entails. I am interested in it for two reasons: first, it may help elucidate some pedagogical concerns such as the relative importance of ordinality and cardinality in the teaching of counting and arithmetic; second, it is suggestive of an ontology of number that is deeply temporal, as well as rhythmic. In fact, I will argue in the next section that the power of ordinality—its capacity to function as a tool or a device—lies precisely in its temporality.
There are at least two strands of research that have attempted to reinstate ordinality into the teaching and learning of mathematics, which I mention briefly here because they support my argument that ontological questions are inseparable from pedagogical ones. The first concerns the work of Caleb Gattegno, who took ordinality as the primary dimension of the developing a concept of number [6, 11]. In Gattegno’s curriculum, there is first a focus on associating number names with number symbols, along with finger gestures. The focus is less on determining the number of fingers that are unfolded than on coordinating different counting myths as well as coordinating counting myths and counting rites. Children then play with Cuisenaire rods (wooden blocks with 1 cm square faces and different lengths—each one associated with a specific colour) and work on relations (such as longer than, shorter than). The first number to be introduced is “2”, to represent the action of placing two rods of the same size to match the length of a single rod. “2” is thus associated not with a single rod, but with a ratio between rods—no matter how long those rods are. But children are not asked “how many?”: numbers are introduced as relations, rather than as denoting objects.2 Further, there is little emphasis on the procedure of how to count. This gives rise to a sense of numbers as relational, rather than being ontologically distinct one from the other; three makes no sense in and of itself, as it might in a cardinal view of number—three is a relation, much as the meaning of one deity coming onto the stage is intertwined with who came before and who is to comes after.
Depending on how one approaches the use of the rods, the emphasis could be more cardinal than ordinal. (Interestingly, this is what often happens in primary school classrooms, and can be seen in the Native Number iPad App, which assigns a specific number to each rod.) If, for example, a teacher chooses to focus on one rod only, and the length is taken to be a discrete multiple of units, then the attention is to cardinality. If, on the other hand, the length is taken to be more continuous, then the quantity ‘2’ is determined by how long it is in relation to another rod. In this latter case, it seems that length is providing the scene for the rite, rather than time.
The primacy of cardinality is also being challenged in the neuroscience literature, which has hypothesised that humans share an early (in evolutionary terms) Approximate Number System (ANS), which is used to judge the relative size of groups of objects in non-symbolic ways [15]. Some of this research suggests that cardinality is the key to learning early number in that it shows a link between ANS and a symbolic awareness of number. However, other researchers have argued that the experiments used in ANS research assume that cardinality is the primary aspect of number [14]. Based on the results of their own experiments, they argue that the “extraction of ordinal information from the ANS” (p. 257) and codifying relations between symbols for numbers may be key. Performing ordinal tasks with number symbols activates different areas of the brain from tasks involving collections of objects (with or without the link to number symbols) [15]. This means that an awareness of relations among number symbols (in an ordinal sense) and an awareness of how to link objects to numbers involve different processes. There is an argument to be made that the former is much more related to the ritual origins of counting. There is also an argument to be made that in developing a concept of number, ordinality is more significant yet much less emphasised in the curriculum.
In the next section, I consider a new App that has been developed to help support children’s early experiences with counting, adding and subtracting. I will use it as an example of what it might look like to re-ontologise number (to move from asking what is number, to what can number be, or become), particularly a concept of ordinal number, in terms of its mobility. This application places children in the phylogenetic world of ordinal numbers.
2 Digital encounters with ordinality
The multi-touch device is a novel technological affordance in mathematics education. Through its direct mediation, it offers opportunities for mathematical expressivity by enabling children to produce and transform screen objects with fingers and gestures, instead of engaging and operating through a keyboard or mouse. This makes it highly accessible, in that children can act and manipulate with their fingers, rather than through symbols and words. It also opens the way for new, tangible forms of mathematical communication. In this section, I describe a new application called TouchCounts, which can be downloaded free of charge from the App Store [20].
TouchCounts is open-ended and exploratory, rather than practice-and level-driven and supports the development of number by offering modes of interaction with number objects that involve fingers and hands. Specifically, it aims both (1) to engage one-to-one correspondence by allowing every finger touch to summon a new sequentially-numbered object into existence, whose appearance is both spoken aloud and symbolically labelled; and (2) to enable gesture-based summing and partitioning—by means of pushing objects together and pulling them apart in a way that exposes very young children to arithmetic operations. Currently, there are two sub-applications in TouchCounts, one for Enumerating and the other for Operating. I will only describe the Enumerating world in this chapter, but readers are invited to visit the website (www.touchcounts.ca) or to download the App to see how the Operating world works.
In the Enumerating world, a user taps her fingers on the screen to summon numbered objects (yellow discs). In the terminology used by Seidenberg, this is the rite. The first tap produces a disc containing the numeral “1”. Subsequent taps produce successively numbered discs. As each tap summons a new numbered disc, TouchCounts audibly speaks the English number word for its number (“one”, “two”, …). This is the myth that accompanies, that narrates, the rite. Fingers can be placed on the screen one at a time or simultaneously. With five successive taps, for instance, five discs (numbered ‘1’ to ‘5’) appear sequentially on the screen, which are counted aloud one by one (see Figure 2a). However, if the user places two fingers on the screen simultaneously, two consecutively numbered discs appear at the same time (Figure 2b), but only the higher-numbered one is named aloud (“two”, if no previous taps have been made). The entire ‘world’ can be reset, to clear all numbered discs and return the ‘count’ of the next summoned disc to one. Note that the discs always arrive in order, pre-baptised, with their symbolic names imprinted upon them.
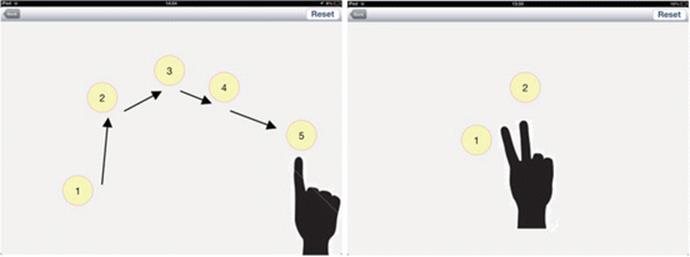
Figure 2
(a) Five sequential taps—“one, two, three, four, five” is said (the arrows are only to indicate the sequence; they are not shown on the screen); (b) A simultaneous two-finger tap—only “two” is said (both discs appear simultaneously)
Earlier, I described the common practice of early school mathematics, which focuses attention on the “how many?” question, where children are asked to count a given set of objects. This question seems to provoke a routine of sequential counting in which the attention is focused on the last word said. In TouchCounts’ Enumerating world, however, the child is engaged in a somewhat different practice—rather than counting a given set, she is actively producing a chain of objects with her finger(s) and these objects seem to count themselves (both aurally and symbolically) as they are summoned into existence. This echoes with Seidenberg’s contention that the origin of counting lies in a creation ritual, in the bringing onto stage the correct deities in the correct order. At the end of the spoken count (the myth), no trace is left of what has been said. On the screen, however, each action leaves a visual trace, one (or more) discs bearing numerals of what has once been summoned into being.
If the ‘gravity’ option for this world is turned on in the App, then as long as the user’s finger remains pressed to the screen, the numbered object holds its position beneath her fingertip. But as soon as she ‘lets go’ (by lifting that finger), the number object falls and then disappears “off” the bottom of the screen, as if captured by some virtual gravity. With ‘gravity’ comes the option of a ‘shelf’, a horizontal line across the screen. If a user releases her numbered object above the shelf, it falls only to the shelf, and comes to rest there, visibly and permanently on screen, rather than vanishing out of sight ‘below’. (Thus, Figure 3 depicts a situation in which there have been four taps below the shelf—these numbered objects were falling—and then a disc labelled ‘5’ was placed above the shelf by tapping above it.) Since each time a finger is placed on the screen, a new numbered disc is created beneath it and, once released by lifting the finger, begins to fall, one cannot “catch” or reposition an existing numbered object by re-tapping it.
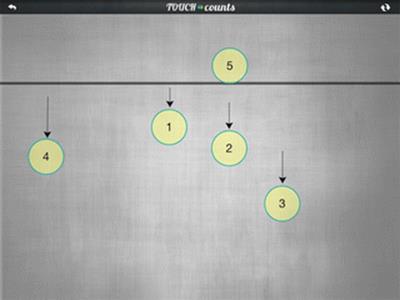
Figure 3
After four sequential taps below the shelf and a fifth tap above the shelf (the yellow discs 1, 2, 3 and 4 will fall off the bottom of the screen)
Discs dropping away (under ‘gravity’) mirror the way spoken language fades rapidly over time, with no trace left—the impermanence of speech. Also, with discs disappearing, any sense of cardinality goes too: the disc labelled ‘2’ is simply the second one to have been summoned by the rite, in the absence of the presence of ‘1’. So the Enumerating world with ‘gravity’ enabled (it is an option) is almost entirely an ordinal one, with the shelf acting as a form of visible memory.
One of the characteristics, then, of TouchCounts is that the computer handles the counting (the iPad is the one who announces and manages the arrival of various figures onto the ritual scene). While the initial design of the App was to support children’s one-to-one correspondence (between pointing and number naming), it quickly became apparent that children could also be corresponding finger touches with number naming, object-creating and symbol-making. This multiplicity of ordinal number production changes what number might mean for these children, as I will describe in these short episodes in which 5- and 6-year-old children play. I will present three episodes in all, each one aiming to highlight the way in which the logical and the ontological are in play.
2.1 “I made 18”
This first episode involves two children, Rodrigo and Grace. In the no-gravity setting, Rodrigo (aged four) was asked to “make five”, which he did by tapping with his left index finger along an imaginary horizontal line from left to right, stopping exactly after TouchCounts said “five”. Grace, aged three, who had not played with TouchCounts before, and who had been watching carefully, said, “I want to do it now”. She started tapping but not saying anything (Figure 4a). She started on the left and then tapped towards the right of the screen along a horizontal, until she reached the edge of the screen at “six” (with TouchCounts counting along). Instead of stopping there, she tapped underneath her numbered disc 1 (thus mirroring writing conventions) and then continued tapping toward the right until she reached the screen edge again, at “twelve”. She then placed the numbered disc 13 under the one showing ‘7’, close to the bottom of the screen, and she tapped until she got to the right edge a third time at “eighteen” (Figure 4b) and then took her finger away from the screen.

Figure 4
(a) Grace tapping on the screen; (b) Grace tapping on the third row; (c) Grace strutting around the classroom shouting, “I made eighteen!”
As mentioned above, the classic exchange in this area of early number starts with the question: “How many?” In the initial prompts here, the teacher asks “How many did you make?”, despite being well aware of the fact that to ask “How many?” presupposes a great deal of awareness and experience about counting. This point provides a strong example of how some of the apparent ‘facts’ about early number are apparently conditioned by the very questions used to ascertain them.
I: How many did you make?
Rodrigo: (Answering for her) Sixteen, seventeen, s’teen. (The sounds before “’teen” are hard to hear, but the words are said in a rhythmic manner as he points in turn to discs on the screen)
Grace: (Looking up at the adult, smiling) Eighteen! (Pointing to the numbered disc 18 at the bottom right of the screen)
I: You made eighteen. (Presses Reset) Now it’s my turn.
Grace: (Gets up and walks away from the group into the middle of the room) I made eighteen! Eighteen, eighteen, eighteen, eighteen, eighteen, eighteen, eighteen. (Marching around the room as she triumphantly calls out – see Figure 4c)
This episode is interesting for several reasons, not least Grace’s excitement at having made eighteen, which was not given as a task, but which emerged from her own exploration. Her pride in having made what she did (which is expressed in her excited “I made eighteen”) underscores the fact that it was indeed she who made it, even though it was not she who initially proclaimed it (the iPad actually said “eighteen”). Her excitement shows how even an arbitrary number (not the more commonly-used ones of primary school, like 5 and 10) can be so interesting.
What is surprising, given her very young age, is the fact that she immediately says “Eighteen!”, rather than counting all the numbered discs again. Perhaps Rodrigo’s mumbling about “teens” oriented her attention to what she had just heard spoken aloud, which dissuaded her from counting them all up. Perhaps because she had made them with her finger, without having to keep count of them herself, she could attend more to the importance of the last spoken number and perhaps associate it with the quantity of discs on the screen.
It is possible to continue counting forever, to go beyond 5 (which Rodrigo did) or 10 (a number she has certainly heard before). This is the logic of seriation. It is important in this context because of the way Grace can count without having to know the number names. She can participate in the rite, while leaving the myth to TouchCounts. The more she does, the more the myth will become her own.
2.2 Putting 10 on the shelf
A group of three children are working together at an after school daycare—one is in kindergarten, another in grade one and the third is in grade two. The teacher has asked the children to place just 10 on the shelf (in the gravity mode). They have done this before, but she imposes an added constraint, which is that they should try to do it in a different way. Whyles goes first. He touches:
with 5 fingers (TouchCounts says “five”),
then 4 fingers (TouchCounts says “nine”)
then 1 finger (TouchCounts says “ten”) above the shelf.
The only thing on the screen was a yellow circle labelled 10 sitting on the shelf. Benford, is next; he touches
with 5 fingers (TouchCounts says “five”),
then 1 finger (TouchCounts says “six”),
then 2 fingers (TouchCounts says “eight”),
then 1 finger (TouchCounts says “nine”)
then puts 1 finger above the shelf (TouchCounts says “ten”).
The only thing on the screen is a yellow circle labelled 10 sitting on the shelf. Finally, Auden, goes next. He touches
with 1 index finger (TouchCounts says “one”)
then 1 pinky finger (TouchCounts says “two”)
then 1 index finger (TouchCounts says “three”)
then 1 middle finger (TouchCounts says “four”)
then 1 index finger (TouchCounts says “five”)
then 1 middle finger (TouchCounts says “six”)
then 1 index finger (TouchCounts says “seven”)
then 1 middle finger (TouchCounts says “eight”)
then 1 index finger (TouchCounts says “nine”)
then 1 middle finger (TouchCounts says “ten”)
There is nothing on the screen except the shelf. Auden presses reset and then touches:
with 1 index finger (TouchCounts says “one”)
then 1 middle finger (TouchCounts says “two”)
then 1 index finger (TouchCounts says “three”)
then 1 pinky finger (TouchCounts says “four”)
then 1 index finger (TouchCounts says “five”)
then 1 middle finger (TouchCounts says “six”)
then 1 index finger (TouchCounts says “seven”)
then 1 middle finger (TouchCounts says “eight”)
then 1 index finger (TouchCounts says “nine”)
then puts 1 index finger above the shelf (TouchCounts says “ten”)
It would be tempting to see these different ways in terms of decompositions of 10, but this would be a cardinal perspective on the number experience. Instead, the actions of the children resembles the setting of a digital clock: like Whyles, you hold the button for awhile, then hold it again, almost as long, until you are close, and then hold briefly for the final touch; Benford was more cautious, with a long hold followed by short holds during the second half; finally, Auden proceeds at a constant pace, alternating between different fingers as he proceeds. The time it takes to get to 10 changes, so that 10 now becomes a more plastic number, rather than a fixed extension.
A concept of number that is more temporal runs the risk of defying the Aristotelian conceit of a strict separation between the mathematical and the physical. In the next section, I draw on some contemporary work in philosophy that offers a different set of assumptions around the relation between the mathematical and physical, a set that not only eschews the banning of time and motion from mathematical concepts, but also rather, on the contrary, celebrates time and motion as significant elements in the creation of new mathematics, and not just as pedagogical devices that can be used to help scaffold novice mathematical understanding.
3 Virtual number
One of the assumptions in education is that children should engage in sensori-motor actions (like pointing at objects) in developing concepts. This view acknowledges the role of the human body in coming to know mathematics, but it does not help explain how these sensori-motor activities turn into mathematical concepts.3 This is sometimes thought to occur through a process of mental abstraction in which, for example, number becomes a concept that is decontextualised, depersonalised and detemporalised. This dualist perspective, which erects a sharp divide between body and mind, can imagine a concept like number as being separate from any particular person, time and place. A contrasting monist perspective, put forth by philosophers such as Gilles Châtelet [5], sees such a concept as always intertwined with person, time and place, so that a concept is not fixed either historically or geographically; mathematics cannot be dissolved from ‘sensible matter’—it is in a perpetual state of becoming. The advantage of this perspective is that it can account for the way a concept can begin, and continue to evolve, as a certain social practice in the physical world. Further, it also explains how concepts can remain alive, open to new forms.
Châtelet posits the virtual as the necessary link that binds the mathematical and the physical together in mutual entailment. His use of the concept of virtual draws on the work of Gilles Deleuze [8], who writes, “[t]he virtual must be defined as strictly a part of the real object – as though the object had one part of itself in the virtual into which it is plunged as though into an objective dimension” (p. 209). It is the virtual dimension of this matter that animates mathematical concepts like number. Mathematical entities are thus material objects with both virtual and actual dimensions. In fact, doing mathematics involves both realising the possible (logical) and actualising the virtual (ontological).
Both realisation and actualisation bring forth something new into the situation (the possible and the virtual), but realisation plays by the rules of logic, while actualisation involves a different kind of determination, one that generates something ontologically new. Châtelet offers the example of mathematician William Rowan Hamilton’s quaternions (which did not come about through logical deduction), as well as the point at infinity (which constituted a new ontological object). The virtual pertains to the indeterminacy at the source of all actions, whereas the possible pertains to the compliance of our actions with logical constraints. Thus novelty, genesis and creativity are fundamental concepts in a theory of actualisation. Actualising the virtual involves “an intrinsic genesis, not an extrinsic conditioning” [8, p. 154]. The virtual in sensible matter becomes intelligible, not by a reductionist abstraction or a “subtraction of determinations” (Aristotle’s approach to abstraction), but by the actions that awaken the virtual.
Châtelet uses many examples from the history of mathematics to exemplify the way in which new kinds of entities are invented by actualising the virtual, such as Hamilton’s quaternions and Abel’s theorem (about indefinite integrals of a rational function). He underscores the important roles that these mathematicians’ gestures and diagrams play in awakening the virtual—by creating new objects, new dimensions, new behaviour. Châtelet draws inspiration from the work of Deleuze, especially in terms of that latter’s interpretation of Leibniz’s “baroque mathematics”. In contrast to modern mathematics, this is a mathematics that offers an alternative starting point for rethinking the relationship between immovable mathematics and movable matter. The term baroque, used in music and architecture, is in part about what is strange or bizarre, but is also about unpredictability and variation, where there might be a medley of contrasting themes instead of a timeless and uniform one. Deleuze considers Leibniz’s approach to the differential calculus to be a baroque one, in that it is concerned with local variability, as is evident in Leibniz’s notion of the family of curves: “Instead of seeking the unique straight tangent in a unique point for a given curve, we can go about seeing the tangent curve in an infinity of points with an infinity of curves: the curve is not touched, it is touching, the tangent no longer either straight, unique or touching, but now being curvilinear, an infinite, touched family” (quoted in [9, p. 19]).
Closer to the focus of this chapter, Deleuze also examines the baroqueness of the irrational number. Unlike the “fractional number”, which has its particular value, “variation becomes presently infinite” with the irrational number as it is the “common limit of the relation between two quantities that are vanishing” (p. 17). Deleuze provides a diagram of an isosceles triangle in which a curved line starting at the vertex C descends towards the straight segment of rational points AB (see Figure 5) and “exposes [AB] as a false infinity” (p. 18). Where the curved line intermingles with the straight line (at X) a point-fold is produced that forms the irrational number as the common limit of two convergent series. The irrational number is not a particular value, nor even a particular ratio (of AX to AB), but an infinite variation.
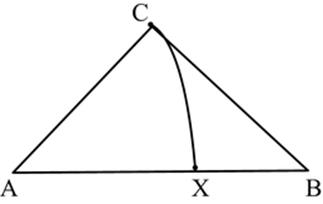
Figure 5
Deleuze’s triangle diagram
Philosophically, Leibniz sees the world as comprised of an infinite number of monads, each with its own distinct point of view and each presupposed by all the others. The ontology of monads feeds into Leibniz’ theories of a relative space–time continuum (spatium) conceived as a fluid of relations and differentials. The monadology is a metaphysical counter to Descartes’ view of nature’s passivity. Within this fluid world of differential relations, actions of any kind are conceived as folds in the spatium. A mathematician’s gesture or diagram creates a new fold on the surface, like the curve cutting the rational segment AB; it pleats and creases matter [9].
As Elizabeth de Freitas and I have shown in [7], novices can also be involved in such inventive acts, provided that there is opportunity for actualising the virtual. We provide the example of a group of grade 1 children doing just this in the context of deciding when two lines will intersect. They first had to extend the surface of the plane beyond the visible one on which lines had been drawn, and then make manifest a point of convergence on this extended plane. This enabled the children to come up with two theories for when two lines will intersect: when the “thickness” between the line changes and when one line is “slanted” more than the other. We underscore the kind of baroque mathematics at work in this example, which we see as significantly related to the dynamic geometry objects that the children were invited to interact with; moving points turned into lines, which also began to move on the screen.
For Grace, the action of repeatedly placing her finger on the screen in order to produce a new object/number/sound can be seen as realising the possible. The actualising of the virtual is in the particular spatial and temporal folds of the making of 18. Because of the way she taps on the screen, 18 is the natural conclusion of the screen size, in that her rows are limited to 6 and her columns to 3. This particular, and likely accidental, arrangement ends up giving 18 a kind of personality of its own that raises it above a mere stepping stone between 17 and 19. Like the Leibnizan monad, 18 gains local perspective from which different directions are possible—it could be the end, as it was in this case, or the number under 12, the launching point for 19, or any other new line of flight. The spacing of the tapping also renders the counting as 1, 2, 3, 4, 5, 6, pause, 7, 8, 9, 10, 11, 12, pause, 13, 14, 15, 16, 17, 18. This is baroque mathematics at work because it breaks free from the equi-ordering of counting, the assumption that each number is the same, modulo position. Grace disrupts this monotony by playing with time, until she pauses at 18. She invents a new way for time to control the count: at the end of the tapping, the count stops. This is what enables Grace to say that she made eighteen: it was not the biggest number, nor the total number, but the last number. Within time, the question of what comes before and after is sorted out. Time provides the order.
In the second example, the realising of the possible relates to a certain kind of order: each new tap will get closer and closer to ten (and might even surpass it). This may seem simple, but it is the very idea that the more you count, the bigger the number gets (where bigger is circumscribed in time), that provides a first way of making sense of the number song. When these children keep tapping, they often go past 100, and even try to get to 1000. The more time it takes for them to get to 100, the bigger their sense of that number. Indeed, in one Kindergarten class, where children played at getting to hundred by repeatedly tapping four times below the shelf and once above, until they got to 200, a child, said “I thought that two hundred was right after one hundred, but it’s not”. The use of “right after” echoes the fact that there were a long sequence of taps between putting 100 on the shelf and placing 200 there—this length of time will eventually become a question of size for the child, but for now it is a fact about ordinality.
In terms of actualising the virtual, it is evident in the children’s new ways of counting. The one, which has been the motor of counting thus far, now flowers into a multiplicity: fives, fours and twos. If one deity at a time was coming on stage before, now we have several (and perhaps, in the Seidenberg sense in which counting by 2s is the origin myth, the real magic is in going from many to one). And not only can we have several, but also we can have different amounts of them (for Whyles and Benford at least). They can also come on stage in a different way (like for Auden, who baptises them with different fingers on different parts of the screen). The ontological function at work here can be seen as a folding of the continuum, where the previously continuous equivalent repetition varies into a continuous non-equivalent repetition.
If a concept is to function both logically and ontologically, it must sustain a certain vibrancy and vitality. In other words, a concept of this kind must be a multi-purpose device that resists reification while carving out new mathematical entities. Châtelet refers to these as ‘allusive devices’ that give rise to thought experiments that “penetrate closer to the heart of relation and operativity” by being deliberately productive of ambiguity [5, (p. 12)]. This seems relevant to the mathematician, who clearly wants concepts that that can be generative, as well as to the mathematics educator or teacher who sees learning as a creative enterprise. Seeing concepts in this way may also help explain some aspects of contemporary school mathematics, in which concepts are overly constrained towards the logical. Based on Châtetet’s historical study of inventive mathematics, de Freitas and I argue that one way to redress the balance is by mobilising mathematics. Putting mathematics into motion reinstates the messier aspects of mathematics: its temporality, in particular, but also its indeterminacy. TouchCounts can be seen as an attempt to mobilise number, which is done in part by focusing on its ordinal nature.
4 Becoming baroque
Seidenberg’s hypothesis about the ritual origins of counting need not be corroborated for it to help answer the question of what number can become. That is because it offers a practice (imaginary or not) in which numbers could come to matter, which may either anticipate or explain unknown practices. This was true in the context of TouchCounts, where the children’s own rituals around tapping and chanting—and, especially, bringing objects on the stage of the shelf—can be seen as a new kind of ordinality that is often overlooked, both in the philosophy of mathematics and in mathematics education. Such an ordinality is intrinsically becoming in the sense that it is thoroughly temporal. And, at least in the context of TouchCounts, it is also tangible and aural, as well as symbolic. It is also becoming in the sense that it has built-in lines of flights; that is, it has both the logical and the ontological so that it is pregnant with the possibility of new meanings. The excerpts that I discussed in the previous two sections provided examples of how these new meanings have emerged in a very particular setting.
As mentioned above, I am not interested, in this chapter, in making a pedagogical argument about the effectiveness of TouchCounts. Instead, I use it as a particular case that enables us to see a kind of ordinality that may be insufficiently appreciated under the pressure of cardinality. There occurred a similar phenomenon with respect to the concept of ratio: the Euclidean approach to ratio effectively replaced the early Greek anthyphairesis (which means reciprocal subtracting in turn—it’s a verb!). These pre-Euclidean ratios were actually a sequence of “repetition numbers”, which effectively cut off a major phylogenetic root [10, p. 31]. Like cardinality, the Euclidean ratio obeys a more static, unitary form. In both cases, re-ontologising these concepts involves the kind of baroque focus on the local, the multiple and the temporal. Rather than argue that history should somehow be respected, and that our sense of what number can be or should be rooted in that history, I am interested in how those particular origins help us understand what number might become, particularly in a radically new digital era in which the hegemony of the alphanumeric (static, linear inscriptions) will give way to visual and dynamic mathematical expressions [18]. In this new world, might a baroque mathematics of the ordinal even give rise to a baroque mathematics of the cardinal?
Acknowledgments
I would like to thank David Pimm for his many helpful comments and discussions about ordinality, the baroque and time. Thanks also to my research team and the children involved in the TouchCounts project.
References
1.
A. Badiou, Number and numbers, Polity Press, 2008.
2.
P. Benaceraff, “What number could not be”, Philosophical Review, vol 74, no. 1 (1964) 47–73.
3.
L. Lunney Borden, “The ‘verbification’ of mathematics: Using the grammatical structures of Mi’kmaq to support student learning”, For the learning of mathematics, vol 31, no. 3 (2011) 8–13.
4.
W. Burkert, Lore and Science in Ancient Pythagoreanism (trans: Minar, E.), Harvard University Press, 1972.
5.
G. Châtelet, Figuring space: philosophy, mathematics and physics, (trans: Shore, R., & Zagha, M.), Kluwer, 2000.
6.
A. Coles, Ordinality, neuro-science and the early learning of number, In C. Nichol, S. Oesterle, P. Liljedahl & D. Allen (Eds), Proceedings of the joint PME 38 and PME-NA 36 conference (Vol. 2, pp. 329–336), Vancouver, BC: PME, 2014.
7.
E. de Freitas, & N. Sinclair, Mathematics and the body: Material entanglements in the classroom, Cambridge University Press, 2014.
8.
G. Deleuze, Difference and repetition (trans: Patton, P.), Columbia University Press, 1994.
9.
G. Deleuze, The fold: Leibniz and the baroque (trans: T. Conley), Athlon Press, 1993.
10.
D. Fowler, The mathematics of Plato’s academy: A new reconstruction, Clarendon Press, 1999.
11.
C. Gattegno, The common sense of teaching mathematics, Educational Solution Worldwide Inc, 1974.
12.
R. Gelman & C.R. Gallistel, The child’s understanding of number, Harvard University Press, 1978.
13.
G. Lakoff & R. Núñez, Where mathematics comes from: How the embodied mind brings mathematics into being, Basic Books, 2000.
14.
I. Lyons & S. Beilock, Numerical ordering ability mediates the relation between number-sense and arithmetic competence, Cognition, vol 121, no. 2 (2011) 256–61.
15.
I. Lyons & S. Beilock, Ordinality and the nature of symbolic numbers, Journal of Neuroscience, vol 33, no. 43 (2013) 17052–17061.
16.
A. Nieder & S. Dehaene, Representation of number in the brain, Annual Review of Neuroscience, vol 32 (2009) 185–208.CrossRef
17.
B. Raglan, The hero: A study in tradition, myth and drama, Greenwood Press, 1936/1975.
18.
B. Rotman, Becoming beside ourselves: The alphabet, ghosts, and distributed human beings, Duke University Press, 2008.
19.
A. Seidenberg, The ritual origin of counting, Archive for History of Exact Sciences, vol 2, no 1 (1962) 1–40.
20.
N. Sinclair & N. Jackiw. TouchCounts [software application for the iPad], 2011, https://itunes.apple.com/ca/app/touchcounts/id897302197?mt=8.
Footnotes
1
Benacerraf [2] plays off this question as well in his paper entitled “What numbers could not be”, which explores the difficulties involved in thinking of numbers as sets of sets.
2
This is in line with the Ancient Greek approach to ‘ratio number’, but markedly different from that of Descartes, for whom a line segment represents “an arbitrarily known number (a “unity”) rather than a number to be measured in numbers” [10, p. 65]. Leibniz will take issue with Descartes’ approach, in its stead creating a “baroque mathematics” that rejects the elemental notion of a unit of measure in favour of continuity and continuous repetition (see [8]).
3
When embodied cognition theorists such as Lakoff and Núñez [13] describe the container metaphor from which the mathematical idea of ‘set’ emerges, they remain committed to an immaterial mathematical concept of set. Moreover, as I will argue, treating all concepts as metaphorical in relation to the ‘real’ reinforces the divide between the mathematically abstract and the physically concrete.