SAT SUBJECT TEST MATH LEVEL 1

SOLID AND COORDINATE GEOMETRY

CHAPTER 13
Coordinate Geometry

THE MIDPOINT OF A SEGMENT

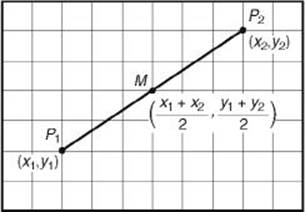
Recall that the midpoint, M, of line segment is the point on such that PM = MQ. In coordinate geometry, the x-coordinate of the midpoint is the average of the x-coordinates of the two endpoints, and the y-coordinate of the midpoint is the average of the y-coordinates of the two endpoints.

Key Fact L4

If P₁(x₁, y₁) and P₂(x₂, y₂) are any two points, then the midpoint, M, of segment is the point whose coordinates are .

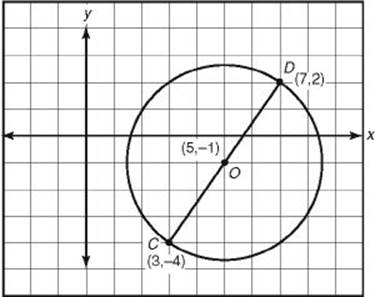
EXAMPLE 3: If C(3, –4) and D(7,2) are the endpoints of diameter CD of circle O, what are the coordinates of O?

First, sketch the circle (see diagram). Since the center of a circle is the midpoint of any diameter, we can use the midpoint formula to find the coordinates of O.

EXAMPLE 4: To find the area of circle O in Example 3, we have to use the formula A = πr ², which means we have to determine r. To do this, we can either find the length of diameter and divide it by 2 or find the length of radius .

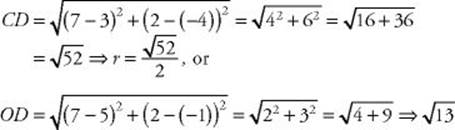
Then, depending on which expression you found,