SAT SUBJECT TEST MATH LEVEL 1
SOLID AND COORDINATE GEOMETRY
![]()
CHAPTER 13
Coordinate Geometry
![]()
SLOPE
The slope of a line is a number that represents how steep it is: the larger the absolute value of the slope, the steeper the line. This intuitive definition is made more precise in KEY FACT L5.
Key Fact L5
• Vertical lines do not have slopes.
• To find the slope of any other line, proceed as follows:
(1) Choose any two points P1(x1, y1) and P2(x2, y2) on the line.
(2) Determine the differences of their y–coordinates, y2– y1, and their x–coordinates, x2– x1.
(3) Divide: slope = ![]() .
.
Since y2 – y1 is the difference between the y–coordinates of the two points and x2 – x1 is the difference between the x–coordinates of the two points, we often say that the slope is “the change in y” over “the change in x”:
![]()
We will illustrate the next KEY FACT by using the slope formula to calculate the slopes of ![]() ,
, ![]() and
and ![]() in the next figure.
in the next figure.
Key Fact L6
• The slope of any horizontal line is 0:
![]()
• The slope of any line that goes up as you move from left to right is positive:
![]()
• The slope of any line that goes down as you move from left to right is negative:
![]()
On the Math 1 test, you may be asked to compare the slopes of lines without being given any coordinates.
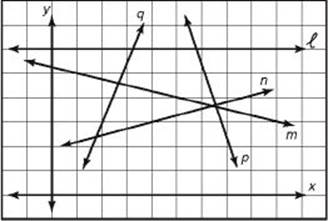
EXAMPLE 5: To list the lines shown in the previous figure in order of increasing slope, first use KEY FACT L6. Since line ![]() is horizontal, its slope is 0. Since as you move from left to right lines m and p go down and lines n and q go up, the slopes of m and p are negative, whereas the slopes of n and q are positive. Since q is steeper than n, the slope of q is greater than the slope of n. Be careful as you compare the slopes of m and p. Line p is steeper than line m, so the absolute value of the slope of p is greater than the absolute value of the slope of m, but this means that the slope of p is less than the slope of m. (For example, |–5| > |–1|, but –5 < –1.) So listed in order of increasing slope we have:
is horizontal, its slope is 0. Since as you move from left to right lines m and p go down and lines n and q go up, the slopes of m and p are negative, whereas the slopes of n and q are positive. Since q is steeper than n, the slope of q is greater than the slope of n. Be careful as you compare the slopes of m and p. Line p is steeper than line m, so the absolute value of the slope of p is greater than the absolute value of the slope of m, but this means that the slope of p is less than the slope of m. (For example, |–5| > |–1|, but –5 < –1.) So listed in order of increasing slope we have:
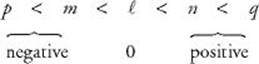
Often, a Math 1 test has at least one question concerning the slopes of parallel and/or perpendicular lines. You will have no trouble answering such questions if you know the next KEY FACT.
Key Fact L7
• If two nonvertical lines are parallel, their slopes are equal.
• If two nonvertical lines are perpendicular, the product of their slopes is –1.
If the product of two numbers, a and b, is –1, then ![]() . So another way to express the second part of KEY FACT L7 is to say that if two nonvertical lines are perpendicular, then the slope of one is the negative reciprocal of the slope of the other.
. So another way to express the second part of KEY FACT L7 is to say that if two nonvertical lines are perpendicular, then the slope of one is the negative reciprocal of the slope of the other.
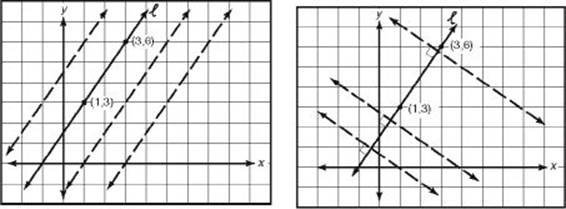
EXAMPLE 6: Let ![]() be the line that passes through points (1, 3) and (3, 6). Then the slope of
be the line that passes through points (1, 3) and (3, 6). Then the slope of ![]() is
is ![]() . If m ||
. If m || ![]() , then the slope of m is also
, then the slope of m is also ![]() . In the figure below left Key Fact L7, each of the dotted lines has a slope of
. In the figure below left Key Fact L7, each of the dotted lines has a slope of ![]() . If n
. If n ![]()
![]() , then the slope of n is –
, then the slope of n is –![]() , the negative reciprocal of
, the negative reciprocal of ![]() . In the figure below right Key Fact L7, each of the dotted lines has a slope of –
. In the figure below right Key Fact L7, each of the dotted lines has a slope of –![]() .
.