SAT SUBJECT TEST MATH LEVEL 1
TRIGONOMETRY
![]()
CHAPTER 14
Basic Trigonometry
![]()
Exercises
![]()
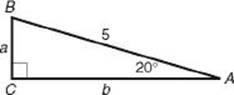
1. In the triangle below, what is the sum of a and b ?
(A) 1.28
(B) 5
(C) 6.41
(D) 7.17
(E) 8.45
2. If 0° < ![]() < 90°, then which of the following is an expression for tan2
< 90°, then which of the following is an expression for tan2![]() cos2
cos2![]() + cos2
+ cos2![]() ?
?
(A) 0
(B) 1
(C) sin2![]()
(D) tan2![]() + 1
+ 1
(E) (tan ![]() cos
cos ![]() + cos
+ cos ![]() )2
)2
3. A ladder is leaning against a wall, forming an angle of 65° with the ground. If the foot of the ladder is 8 feet from the wall, what is the length of the ladder, in feet?
(A) 3.38
(B) 7.25
(C) 8.83
(D) 17.15
(E) 18.93
4. If 0° < ![]() < 90° and tan
< 90° and tan ![]() = 5, what is sin
= 5, what is sin ![]() + cos
+ cos ![]() ?
?
(A) 0.19
(B) 0.85
(C) 1
(D) 1.18
(E) 5.2
5. If 0° < ![]() < 90°, then which of the following is equivalent to
< 90°, then which of the following is equivalent to ![]()
(A) 1
(B) ![]()
(C) 1 + tan ![]()
(D) ![]()
(E) cos ![]() + tan
+ tan ![]() sin
sin ![]()
6. What is the measure of the smallest angle in a 5=12=13 right triangle?
(A) 15°
(B) 21°
(C) 22.6°
(D) 45°
(E) 67.4°
7. If ![]() ABC is isosceles and m∠C = 90°, which of the following must be true?
ABC is isosceles and m∠C = 90°, which of the following must be true?
I. tan A = 1
II. sin A = cos A
III. sin A = cos B
(A) I only
(B) II only
(C) III only
(D) I and II only
(E) I, II, and III
8. Which of the following is equal to (3 sin2 ![]() )(4 sin2
)(4 sin2 ![]() ) + (2 cos2
) + (2 cos2 ![]() )(6 cos2
)(6 cos2 ![]() )?
)?
(A) 1
(B) 2
(C) 6
(D) 12
(E) 24
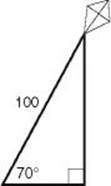
9. A kite string is tied to a peg in the ground. If the angle formed by the string and the ground is 70° and if there is 100 feet of string out, to the nearest foot, how high above the ground is the kite?
(A) 34
(B) 64
(C) 74
(D) 94
(E) 274
10. If 0° < ![]() < 90°, which of the following is equivalent to
< 90°, which of the following is equivalent to ![]()
(A) –1
(B) 1
(C) sin2![]() – cos2
– cos2![]()
(D) cos2![]() – sin2
– sin2![]()
(E) tan2![]() – cos2
– cos2![]()
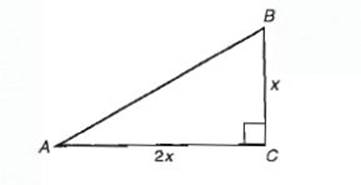
11. If the longer leg of a right triangle is twice as long as the shorter leg, what is the ratio of the measure of the larger acute angle to the measure of the smaller acute angle?
(A) 0.42
(B) 0.50
(C) 1.78
(D) 2.00
(E) 2.39
12. A car is parked 120 feet from a building that is 350 feet tall. What is the measure of the angle of depression from the top of the building to the car?
(A) 18.9°
(B) 37.8°
(C) 64.2°
(D) 71.1°
(E) 78.6°
ANSWERS EXPLAINED
Answer Key
|
1. (C) |
5. (B) |
9. (D) |
||
|
2. (B) |
6. (C) |
10. (A) |
||
|
3. (E) |
7. (E) |
11. (E) |
||
|
4. (D) |
8. (D) |
12. (D) |
SOLUTIONS
Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the model tests in this book and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you do not have to leave them out—you can almost always answer them by using one or more of the strategies discussed in the “Tactics” chapter. The solutions given here do not depend on those strategies; they are the correct mathematical ones.
See Important Tactics for an explanation of the symbol ⇒, which is used in several answer explanations.
![]() 1. (C) Use the sine and cosine ratios:
1. (C) Use the sine and cosine ratios:
sin 20° = ![]()
![]() a = 5 (sin 20°)= 5(0.342)= 1.710
a = 5 (sin 20°)= 5(0.342)= 1.710
cos 20° = ![]()
![]() b = 5 (cos 20°)= 5(0.940)= 4.700
b = 5 (cos 20°)= 5(0.940)= 4.700
So a + b = 1.710 + 4.700 = 6.41
2. (B) tan2![]() cos2
cos2![]() + cos2
+ cos2![]() =
= 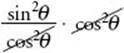 + cos2
+ cos2![]() = sin2
= sin2![]() + cos2
+ cos2![]() =1
=1
3. (E) First draw a diagram.
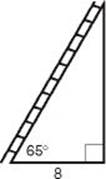
By using the cosine ratio, we get that cos 65° = ![]() , where L represents the length of the ladder.
, where L represents the length of the ladder.
![]() L cos 65° = 8
L cos 65° = 8 ![]()
L = 8 ![]() (cos 65°) = 18.93
(cos 65°) = 18.93
4. (D) Draw a right triangle. Since ![]() , label the side opposite
, label the side opposite ![]() as 5 and the side adjacent to
as 5 and the side adjacent to ![]() as 1.
as 1.
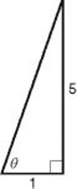
Then use the Pythagorean theorem to find the hypotenuse:
12+52=c2![]() c2=1+25=26
c2=1+25=26![]() c=
c= ![]()
So sin ![]() =
= ![]() and cos
and cos ![]() =
= ![]() Then:
Then:
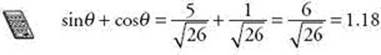
Alternatively, you could have found that ![]() = tan–1(5) = 78.69° and then added sin78.69 + cos78.69 = 1.18.
= tan–1(5) = 78.69° and then added sin78.69 + cos78.69 = 1.18.
5. (B) 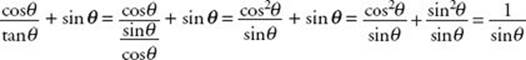
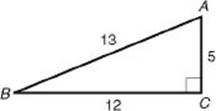
![]() 6. (C) Draw and label a 5-12-13 right triangle. The smallest angle is B, the angle opposite the smallest side. Since sin
6. (C) Draw and label a 5-12-13 right triangle. The smallest angle is B, the angle opposite the smallest side. Since sin ![]() , we have B = sin-1
, we have B = sin-1![]() = 22.6°.
= 22.6°.
7. (E) Sketch isosceles right ![]() ABC with AC = BC and m∠A = m∠B = 45°.
ABC with AC = BC and m∠A = m∠B = 45°.
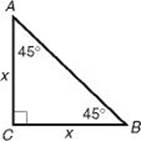
Then tan ![]() (I is true). sinA, cosA, sinB, and cosB are all equal to
(I is true). sinA, cosA, sinB, and cosB are all equal to ![]() (II and III are true). Note that sin45° = cos45° = 0.707.
(II and III are true). Note that sin45° = cos45° = 0.707.
8. (D) (3 sin2 ![]() )(4 sin2
)(4 sin2 ![]() ) = 12 sin22
) = 12 sin22 ![]()
(2 cos 2 ![]() )(6 cos 2
)(6 cos 2 ![]() ) = 12 cos2 2
) = 12 cos2 2 ![]()
So, (3 sin 2 ![]() )(4 sin 2
)(4 sin 2 ![]() ) + (2 cos 2
) + (2 cos 2 ![]() )(6 cos 2
)(6 cos 2 ![]() ) = 12 sin2 2
) = 12 sin2 2![]() + 12 cos2 2
+ 12 cos2 2 ![]() = 12(sin2 2
= 12(sin2 2 ![]() + cos2 2
+ cos2 2 ![]() ) = 12(1) = 12
) = 12(1) = 12
![]() 9. (D) If x represents the height of the kite, then
9. (D) If x represents the height of the kite, then
sin 70° = ![]()
![]() x = 100 sin 70° = 100(0.9396) = 93.96
x = 100 sin 70° = 100(0.9396) = 93.96 ![]() 94.
94.
10. (A) Since a4 – b4 = (a2 – b2)(a2 + b2):
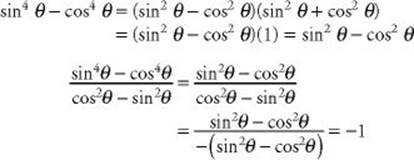
11. (E) Draw and label a diagram. Then:
![]()
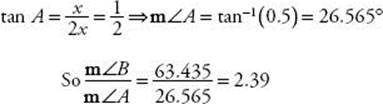
12. (D) Draw a diagram and label it.
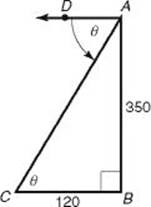
The angle of depression, ∠DAC, is the angle between the line of sight and the horizontal and by KEY FACT G6 is congruent to ∠C. Since ![]()