SAT SUBJECT TEST MATH LEVEL 2
PART 3
![]()
MODEL TESTS
![]()
Answer Sheet
MODEL TEST 2

Model Test 2
![]()
|
The following directions are for the print book only. Since this is an e-Book, record all answers and self-evaluations separately. |
Tear out the preceding answer sheet. Decide which is the best choice by rounding your answer when appropriate. Blacken the corresponding space on the answer sheet. When finished, check your answers with those at the end of the test. For questions that you got wrong, note the sections containing the material that you must review. Also, if you do not fully understand how you arrived at some of the correct answers, you should review the appropriate sections. Finally, fill out the self-evaluation chart in order to pinpoint the topics that give you the most difficulty.
|
50 questions: 1 hour Directions: Decide which answer choice is best. If the exact numerical value is not one of the answer choices, select the closest approximation. Fill in the oval on the answer sheet that corresponds to your choice. Notes: (1) You will need to use a scientific or graphing calculator to answer some of the questions. (2) You will have to decide whether to put your calculator in degree or radian mode for some problems. (3) All figures that accompany problems are plane figures unless otherwise stated. Figures are drawn as accurately as possible to provide useful information for solving the problem, except when it is stated in a particular problem that the figure is not drawn to scale. (4) Unless otherwise indicated, the domain of a function is the set of all real numbers for which the functional value is also a real number. |
|
Reference Information. The following formulas are provided for your information. Volume of a right circular cone with radius r and height Lateral area of a right circular cone if the base has circumference C and slant height is l: Volume of a sphere of radius Surface area of a sphere of radius r : S = 4 Volume of a pyramid of base area B and height |
1. If ![]() , for what value(s) of x does the graph of f(x ) have a vertical asymptote?
, for what value(s) of x does the graph of f(x ) have a vertical asymptote?
(A) –2, 0, and 2
(B) –2 and 2
(C) 2
(D) 0
(E) –2
2. What is the distance between the points with coordinates (−3,4,1) and (2,7,−4)?
(A) 5.24
(B) 7.68
(C) 11.45
(D) 13.00
(E) 19.26
3. Log (a2 – b2) =
(A) log a2 – log b2
(B) ![]()
(C) ![]()
(D) 2 · log a − 2 · log b
(E) log (a + b ) + log (a − b )
4. The sum of the roots of the equation ![]()
(A) 1.9
(B) 2.2
(C) 2.5
(D) 3.3
(E) 6.8
5. If the graph of x + 2y + 3 = 0 is perpendicular to the graph of ax + 3y + 2 = 0, then a equals
(A) –6
(B) – ![]()
(C) ![]()
(D) ![]()
(E) 6
6. The maximum value of 6 sin x cos x is
(A) ![]()
(B) 1
(C) 2.6
(D) 3
(E) 6
7. If f(r ,![]() ) = r cos
) = r cos![]() , then f(2,3)=
, then f(2,3)=
(A) –3.00
(B) –1.98
(C) 0.10
(D) 1.25
(E) 2.00
8. If 5 and –1 are both zeros of the polynomial P(x), then a factor of P(x) is
(A) x2 – 5
(B) x2 – 4x + 5
(C) x2 + 4x – 5
(D) x2 + 5
(E) x2 – 4x – 5
9. i14 + i15 + i16 + i17=
(A) 0
(B) 1
(C) 2i
(D) 1 – i
(E) 2 + 2i
10. When the graph of y = sin 2x is drawn for all values of x between 10° and 350°, it crosses the x-axis
(A) zero times
(B) one time
(C) two times
(D) three times
(E) six times
11. The third term of an arithmetic sequence is 15, and the seventh term is 23. What is the first term?
(A) 1
(B) 6
(C) 9
(D) 11
(E) 13
12. A particular sphere has the property that its surface area has the same numerical value as its volume. What is the length of the radius of this sphere?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 6
13. ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
14. The pendulum on a clock swings through an angle of 1 radian, and the tip sweeps out an arc of 12 inches. How long is the pendulum?
(A) 3.8 inches
(B) 6 inches
(C) 7.6 inches
(D) 12 inches
(E) 35 inches
15. What is the domain of the function ![]()
(A) x ![]() 1.33
1.33
(B) x ![]() 1.53
1.53
(C) x ![]() 2.33
2.33
(D) x ![]() –1.33 or x
–1.33 or x ![]() 1.33
1.33
(E) x ![]() –2.33 or x
–2.33 or x ![]() 2.33
2.33
16. If x + y = 90°, which of the following must be true?
(A) cos x = cos y
(B) sin x = –sin y
(C) tan x = cot y
(D) sin x + cos y = 1
(E) tan x + cot y = 1
17. The graph of the equation y = x3 + 5x + 1
(A) does not intersect the x-axis
(B) intersects the x-axis at one and only one point
(C) intersects the x-axis at exactly three points
(D) intersects the x-axis at more than three points
(E) intersects the x-axis at exactly two points
18. The length of the radius of the sphere x2 + y2 + z2 + 2x – 4y = 10 is
(A) 3.16
(B) 3.38
(C) 3.46
(D) 3.74
(E) 3.87
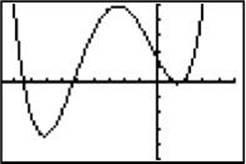
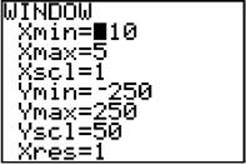
19. The graph of y = x4 + 11x3 + 9x2 – 97x + c is shown above with the window shown below it. Which of the following values could be c ?
(A) –2820
(B) –80
(C) 80
(D) 250
(E) 2820
20. Which of the following is the solution set for x (x – 3)(x + 2) > 0?
(A) x < –2
(B) –2 < x < 3
(C) –2 < x < 3 or x > 3
(D) x < –2 or 0 < x < 3
(E) –2 < x < 0 or x > 3
21. Which of the following is the equation of the circle that has its center at the origin and is tangent to the line with equation 3x – 4y = 10?
(A) x2 + y2 = 2
(B) x2 + y2 = 4
(C) x2 + y2 = 3
(D) x2 + y2 = 5
(E) x2 + y2 = 10
22. If f(x) = 3 – 2x + x2, then ![]()
(A) t2 + 2xt – 2t
(B) x2t2 – 2xt + 3
(C) t + 2x – 2
(D) 2x – 2
(E) none of the above
23. If f(x) = x3 and g(x) = x2 + 1, which of the following is an odd function (are odd functions)?
I. f(x) ![]() g(x)
g(x)
II. f(g(x))
III. g(f(x))
(A) only I
(B) only II
(C) only III
(D) only II and III
(E) I, II, and III
24. In how many ways can a committee of four be selected from nine men so as to always include a particular man?
(A) 48
(B) 56
(C) 70
(D) 84
(E) 126
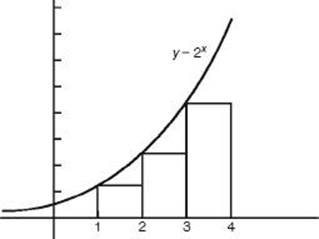
25. The figure above shows a portion of the graph of y = 2x. What is the sum of the areas of the three inscribed rectangles shown?
(A) 14
(B) 28
(C) 128
(D) 256
(E) 384
26. If the mean of the set of data 1, 2, 3, 1, 2, 5, x is ![]() what is the value of x ?
what is the value of x ?
(A) –10.7
(B) 2.5
(C) 5.6
(D) 7.4
(E) 8.9
27. In ![]() JKL,sin L =
JKL,sin L = ![]() ,sin J =
,sin J = ![]() , and JK =
, and JK = ![]() inches. The length of KL , in inches, is
inches. The length of KL , in inches, is
(A) 1.7
(B) 3.0
(C) 3.5
(D) 3.9
(E) 4.0
28. Matrix X has r rows and c columns, and matrix Y has c rows and d columns, where r, c, and d are different. Which of the following statements must be false?
I. The product YX exists
II. The product of XY exists and has r rows and d columns.
III. The product XY exists and has c rows and c columns.
(A) I only
(B) II only
(C) III only
(D) I and II
(E) I and III
* 29. Which of the following statements is logically equivalent to: “If he studies, he will pass the course.”
(A) He passed the course; therefore, he studied.
(B) He did not study; therefore, he will not pass the course.
(C) He did not pass the course; therefore he did not study.
(D) He will pass the course only if he studies.
(E) None of the above.
30. If f(x) = x – 7 and g(x) = ![]() , what is the domain of g o f?
, what is the domain of g o f?
(A) x ![]() 0
0
(B) x ![]() –7
–7
(C) x ![]() 0
0
(D) x ![]() 7
7
(E) all real numbers
31. In ![]() ABC, a = 1, b = 4, and
ABC, a = 1, b = 4, and ![]() C = 30°. The length of c is
C = 30°. The length of c is
(A) 4.6
(B) 3.6
(C) 3.2
(D) 2.9
(E) 2.3
32. The solution set of 3x + 4y < 0 lies in which quadrants?
(A) I only
(B) I and II
(C) I, II, and III
(D) II, III, and IV
(E) I, II, III, and IV
*Logic questions such as this have appeared on past SAT Math Level 2 exams.
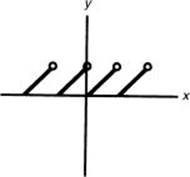
33. Which of the following could represent the inverse of the function graphed above?
(A) 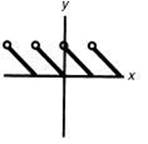
(B) 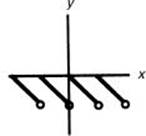
(C) 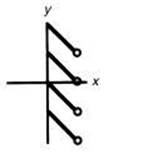
(D) 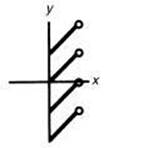
(E) 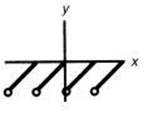
34. If f is a linear function and f(–2) = 11, f(5) = –2, and f(x) = 4.3, what is the value of x?
(A) –3.1
(B) –1.9
(C) 1.6
(D) 2.9
(E) 3.2
35. A taxicab company wanted to determine the fuel cost of its fleet. A sample of 30 vehicles was selected, and the fuel cost for the last month was tabulated for each vehicle. Later it was discovered that the highest amount was mistakenly recorded with an extra zero, so it was 10 times the actual amount. When the correction was made, this was still the highest amount. Which of the following must have remained the same after the correction was made?
(A) mean
(B) median
(C) mode
(D) range
(E) standard deviation
36. The range of the function ![]() is
is
(A) y < 0
(B) y > 0
(C) y ![]() 0
0
(D) y ![]() 0
0
(E) all real numbers
37. The formula A = Pe0.04t gives the amount A that a savings account will be worth if an initial investment P is compounded continuously at an annual rate of 4 percent for t years. Under these conditions, how many years will it take an initial investment of $10,000 to be worth approximately $25,000?
(A) 1.9
(B) 2.5
(C) 9.9
(D) 22.9
(E) 25.2
38. A coin is tossed three times. Given that at least one head appears, what is the probability that exactly two heads will appear?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
39. A unit vector parallel to vector ![]() = (2,−3,6) is vector
= (2,−3,6) is vector
(A) (–2, 3, –6)
(B) (6, –3, 2)
(C) (–0.29, 0.43, –0.86)
(D) (0.29, 0.43, –0.86)
(E) (–0.36, –0.54, 1.08)
40. What is the equation of the horizontal asymptote of the function 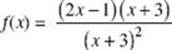
(A) y = –9
(B) y = –3
(C) y = 0
(D) y = ![]()
(E) y = 2
41. The points in the rectangular coordinate plane are transformed in such a way that each point A(x,y) is moved to a point A'(kx,ky). If the distance between a point A and the origin is d, then the distance between the origin and the point A' is
(A) ![]()
(B) ![]()
(C) d
(D) kd
(E) d2
42. A committee of 5 people is to be selected from 6 men and 9 women. If the selection is made randomly, what is the probability that the committee consists of 3 men and 2 women?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
43. Three consecutive terms, in order, of an arithmetic sequence are ![]() . Then x equals
. Then x equals
(A) 2.14
(B) 2.45
(C) 2.46
(D) 3.24
(E) 3.56
44. The graph of xy – 4x – 2y – 4 = 0 can be expressed as a set of parametric equations. If ![]() and x = f (t), then f(t) =
and x = f (t), then f(t) =
(A) t + 1
(B) t – 1
(C) 3t – 3
(D) ![]()
(E) ![]()
45. If f(x) = ax2 + bx + c , how must a and b be related so that the graph of f(x – 3) will be symmetric about the y-axis?
(A) a = b
(B) b = 0, a is any real number
(C) b = 3a
(D) b = 6a
(E) ![]()
46. The graph of y = log5 x and y = ln 0.5x intersect at a point where x equals
(A) 6.24
(B) 5.44
(C) 1.69
(D) 1.14
(E) 1.05
47. What is the value of x if ![]() and sin x = 5 cos x ?
and sin x = 5 cos x ?
(A) 3.399
(B) 3.625
(C) 4.515
(D) 4.623
(E) 4.663
48. The area of the region enclosed by the graph of the polar curve ![]() and the x- and y-axes is
and the x- and y-axes is
(A) 0.48
(B) 0.50
(C) 0.52
(D) 0.98
(E) 1.00
49. A rectangular box has dimensions of length = 6, width = 4, and height = 5. The measure of the angle formed by a diagonal of the box with the base of the box is
(A) 27°
(B) 35°
(C) 40°
(D) 44°
(E) 55°
50. If (x,y) represents a point on the graph of y = 2x + 1, which of the following could be a portion of the graph of the set of points (x,y2)?
(A) 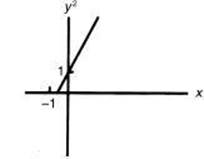
(B) 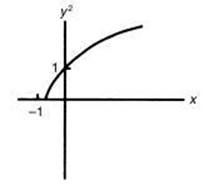
(C) 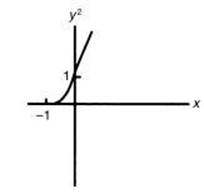
(D) 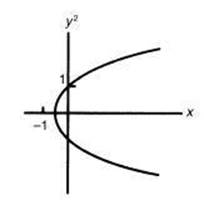
(E) 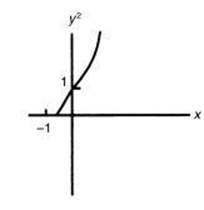

If there is still time remaining, you may review your answers.
Answer Key
MODEL TEST 2
|
|
|
|
ANSWERS EXPLAINED
The following explanations are keyed to the review portions of this book. The number in brackets after each explanation indicates the appropriate section in the Review of Major Topics (Part 2). If a problem can be solved using algebraic techniques alone, [algebra] appears after the explanation, and no reference is given for that problem in the Self-Evaluation Chart at the end of the test.
An asterisk appears next to those solutions in which a graphing calculator is necessary.
1. * (E) Graph the function f in the standard window and observe the vertical asymptote at x = –2.
An alternative solution is to factor the denominator of f as (x + 2)(x – 2); cancel the factor x – 2 in the numerator and denominator so that ![]() ; and recall that a function has a vertical asymptote when the denominator is zero and the numerator isn’t. There is a hole in the graph of fat x = 2. [1.5]
; and recall that a function has a vertical asymptote when the denominator is zero and the numerator isn’t. There is a hole in the graph of fat x = 2. [1.5]
2. * (A) Use the distance formula for three-dimensional space:
![]()
3. (E) Log(a2 – b2) = log(a + b)(a – b) = log(a + b) + log(a – b). [1.4]
4. * (D) The sum of the roots is ![]() +
+ ![]() + (–
+ (– ![]() ) +
) + ![]()
![]() 1.414 + 1.414 – 1.732 + 2.236
1.414 + 1.414 – 1.732 + 2.236 ![]() 3.3. [1.2]
3.3. [1.2]
5. (A) The slope of the first line is –![]() , and the slope of the second is –
, and the slope of the second is –![]() . To be perpendicular, –
. To be perpendicular, –![]() = –
= –![]() , or a = –6. [1.2]
, or a = –6. [1.2]
6. * (D) Plot the graph of 6 sin x cos x using ZTrig and observe that the max of this function is 3. (None of the other answer choices is close. If one were, you could use CALC/max to find the maximum value of the function.)
An alternative solution is to recall that 2x = 2 sin x cos x, so that 6 sin x cos x = 3 sin2x. Since the amplitude of sin 2x is 1, the amplitude of 3 sin 2x is 3. [1.3]
7. * (B) Put your calculator in radian mode. f(2,3) = 2 · cos 3 ![]() 2(–0.98999)
2(–0.98999) ![]() –1.98. [2.1]
–1.98. [2.1]
8. (E) Since 5 and –1 are zeros, x – 5 and x + 1 are factors of P(x), so their product x2 – 4x – 5 is too. [1.2]
9. * (A) Enter the expression into your graphing calculator. [3.2]
10. * (D) Plot the graph of y = sin 2x in degree mode in an ![]() window and observe that the graph crosses the axis 3 times.
window and observe that the graph crosses the axis 3 times.
An alternative explanation uses the fact that the function sin 2x has period ![]() and the fact that sin 2x = 0 when 2x = 0°,180°,360°,540°,720°, . . . , or when x = 0°,90°,180°,270°,360°, . . . Three values of x lie between 10° and 350°. [1.3]
and the fact that sin 2x = 0 when 2x = 0°,180°,360°,540°,720°, . . . , or when x = 0°,90°,180°,270°,360°, . . . Three values of x lie between 10° and 350°. [1.3]
11. (D) The third and seventh terms are 4 terms apart, and the difference between them is 8. Therefore, the common difference is 8 ÷ 4 = 2. Since the first term is two terms prior to the third term, its value is 15 – 2(2) = 11. [3.4]
12. (C) Surface area = 4πr2. Volume ![]() Solve 4πr2
Solve 4πr2 ![]() to get r = 3. [2.2]
to get r = 3. [2.2]
13. (D) To add, form the common denominator ab. Solve ![]()
14. (D) s = r![]() . 12 = r. [1.3]
. 12 = r. [1.3]
15. * (A) The domain consists of all numbers that make 3x3 – 7 ![]() 0. Therefore,
0. Therefore, ![]() and x
and x ![]() 1.33. [1.1]
1.33. [1.1]
16. (C) Cofunctions of complementary angles are equal. Since x and y are complementary, tan and cot are cofunctions.
An alternative solution is to choose any values of x and y such that their sum is 90°. (For example, x = 40° and y = 50°.) Test the answer choices with your calculator in degree mode to see that only Choice C is true. [1.3]
17. (B) Plot the graph of y = x3 + 5x + 1 in the standard window and zoom in a couple of times to see that it crosses the x-axis only once. To make sure you are not missing anything, you should also plot the equation in a x![]() [–1,1], y
[–1,1], y![]() [–1,1] and an x
[–1,1] and an x![]() [–100,100], y
[–100,100], y![]() [–100,100] window.
[–100,100] window.
An alternative solution is to use Descartes’ Rule of Signs, which indicates that the graph does not intersect the positive x-axis, but it does intersect the negative x-axis once. [1.2]
18. * (E) Complete the square in x and y: (x2 + 2x + 1) + (y2 – 4y + 4) + z2 = 10 + 1 + 4, so (x + 1)2 + (y – 2)2 + z2 = 15. Therefore, r = ![]()
![]() 3.87. [2.2]
3.87. [2.2]
19. (C) If you substitute 0 for x you get c, so c is the y-intercept of the graph. The graph and window indicate that this value is about 80. [1.2]
20. * (E) Plot the graph of y = x(x – 3)(x + 2) in the standard window, and observe that the graph is above the x-axis when –2 < x < 0 or when x > 3.
An alternative solution is to find the zeros of the function x(x – 3)(x + 2) as x = 0,3,–2 and test points in the intervals established by these zeros. Points between –2 and 0 and greater than 3 satisfy the inequality. [1.2]
21. * (B) Use the correct formula to calculate the distance between the point (0,0) and the line 3x – 4y = 10 as 2. Therefore, the radius of the circle is 2, and its equation is x2 + y2 = 4. [2.2]
22. (C) 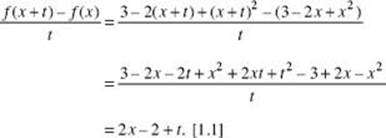
|
CAUTION: For calculus students only: This difference quotient looks like the definition of the derivative. However, no limit is taken, so don’t jump at f '(x), which is Choice D. |
23. * (A) Enter x3 into Y1 and x2 + 1 into Y2. Then enter Y1Y2 into Y3; Y1(Y2) into Y4; and Y2(Y1) into Y5. De-select Y1 and Y2. Inspection of Y3, Y4, and Y5 shows that only Y3 is symmetric about the origin.
An alternative solution is to define each of the three functions as h(x) and check each against the definition of an odd function, h(–x) = –h(x):
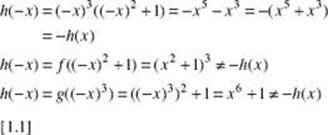
24. * (B) Since one particular man must be on the committee, the problem becomes: “Form a committee of 3 from 8 men.” Calculate 8nCr3 = 56. [3.1]
25. (A) Each rectangle has width 1. The heights of these rectangles are 21 = 2, 22 = 4, and 23 = 8. The sum of these areas is 14. [1.4]
26. * (E) Mean ![]() Therefore, x = 8.9. [4.1].
Therefore, x = 8.9. [4.1].
27. * (E) Law of sines: 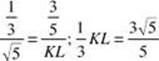 .
.
Therefore, ![]()
28. (B) Multiplication of matrices is possible only when the number of columns in the matrix on the left equals the number of rows in the matrix on the right. In that case, the product is a matrix with the number of rows in the left-hand matrix and the number of columns of the right-hand matrix. [3.3]
29. (C) Relative to the statement, answer choice A is the converse, B is the inverse, C is the contrapositive, and D is another form of the inverse. Of these, the contrapositive is the logical equivalent of the original statement. [logic]
30. (D) (g o f)(x) = g(f(x)) = ![]() . Therefore, x
. Therefore, x ![]() 7. [1.1]
7. [1.1]
31. * (C) Law of cosines: ![]() . Therefore, c
. Therefore, c ![]() 3.2. [1.3]
3.2. [1.3]
32. * (D) Use the standard window to graph ![]() , by moving the cursor all the way left (past Y =) and keying Enter until a “lower triangle” is observed. The shaded portion of the graph will lie in all but Quadrant I.
, by moving the cursor all the way left (past Y =) and keying Enter until a “lower triangle” is observed. The shaded portion of the graph will lie in all but Quadrant I.
An alternative solution is to graph the related equation ![]() and test points to determine which side of the line contains solutions to the inequality. This will indicate the quadrant that the graph does not enter. [1.2]
and test points to determine which side of the line contains solutions to the inequality. This will indicate the quadrant that the graph does not enter. [1.2]
33. (D) Fold the graph about the line y = x, and the resulting graph will be Choice D. [1.1]
34. * (C) Since these points are on a line, all slopes must be equal.
Slope ![]() . Cross-multiplying the far right equation gives –13(x + 2) = 7(–6.7), and solving for x yields x
. Cross-multiplying the far right equation gives –13(x + 2) = 7(–6.7), and solving for x yields x ![]() 1.6. [1.2]
1.6. [1.2]
35. (B) Since the median is the middle value, it does not change if the number (quantity) of values above and below it remain the same. [4.1]
36. * (B) Plot the graph of y = x–2/3 in the standard window and observe that the entire graph lies above the x-axis.
An alternative solution uses the fact that ![]() , and x2/3 = (x1/3)2, so that for all values of x (except zero) y is positive. Therefore, the range of y = x–2/3 is y > 0. [1.1]
, and x2/3 = (x1/3)2, so that for all values of x (except zero) y is positive. Therefore, the range of y = x–2/3 is y > 0. [1.1]
37. * (D) Substitute the given values into the formula to get 25000 = 10000e0.04t. To solve for t, first divide both sides by 10000. Then take logarithms (either ln or log) of both sides to get ln2.5 = 0.04t. Therefore ![]()
38. (B) There are 8 elements in the sample space of a coin being flipped 3 times. Of these elements, 7 contain at least 1 head and 3 (HHT, HTH, THH) contain 2 heads.
Probability = ![]()
39. * (C) To find a unit vector parallel to (2,–3,6), divide each component by ![]() . There are two unit vectors, pointing in opposite directions, that meet this requirement: (0.29,–0.43,0.86) and (–0.29,0.43,–0.86). Only the second one is an answer choice. [3.5]
. There are two unit vectors, pointing in opposite directions, that meet this requirement: (0.29,–0.43,0.86) and (–0.29,0.43,–0.86). Only the second one is an answer choice. [3.5]
40. (E) To find the horizontal asymptote, you need to see what happens when x gets much larger (![]() ) or much smaller (
) or much smaller (![]() ). With the numerator and denominator expanded,
). With the numerator and denominator expanded, ![]() . Divide both by x2 to see that y approaches 2 as x gets much bigger or smaller. [1.5]
. Divide both by x2 to see that y approaches 2 as x gets much bigger or smaller. [1.5]
41. (D) The distance between the origin and A is d =![]() . The distance between the origin and A' is
. The distance between the origin and A' is ![]()
42. * (B) There are ![]() ways of selecting a committee of 5 out of 15 people (men and women). There are
ways of selecting a committee of 5 out of 15 people (men and women). There are ![]() ways of selecting 3 men of 6, and for each of these, there are
ways of selecting 3 men of 6, and for each of these, there are ![]() ways of selecting 2 women of 9. Therefore, there are
ways of selecting 2 women of 9. Therefore, there are ![]() ways of selecting 3 men and 2 women. The probability of selecting 3 men and 2 women is
ways of selecting 3 men and 2 women. The probability of selecting 3 men and 2 women is 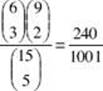 . Using the calculator command
. Using the calculator command ![]() , enter this expression and change to a fraction. [3.1, 4.2]
, enter this expression and change to a fraction. [3.1, 4.2]
43. * (A) 2x + ![]() = (x +
= (x + ![]() ) + d, and 5x –
) + d, and 5x – ![]() = (2x +
= (2x + ![]() ) + d. Eliminate d, and x +
) + d. Eliminate d, and x + ![]() –
– ![]() = 3x –
= 3x – ![]() –
– ![]() . Thus,
. Thus, ![]() . [3.4]
. [3.4]
44. (B) Substituting for y gives ![]() , which simplifies to 12x – 12t + 12 = 0. Then x = t – 1. [1.6]
, which simplifies to 12x – 12t + 12 = 0. Then x = t – 1. [1.6]
45. (D) The graph of the function is a parabola, and the equation of its axis of symmetry is ![]() . Since the graph of y = f(x – 3) is the translation of y = f(x) 3 units to the right, f(x – 3) will be symmetric about the y-axis when f(x) is symmetric about –3. Therefore,
. Since the graph of y = f(x – 3) is the translation of y = f(x) 3 units to the right, f(x – 3) will be symmetric about the y-axis when f(x) is symmetric about –3. Therefore, ![]() , or b = 6a. [1.2]
, or b = 6a. [1.2]
46. * (A) Use the change of base formula and graph ![]() as Y1. Graph y = ln(0.5x) as Y2. The answer choices suggest a window of x
as Y1. Graph y = ln(0.5x) as Y2. The answer choices suggest a window of x![]() [0,10] and y
[0,10] and y![]() [0,2]. Use the CALC/intersect to find the correct answer choice A.
[0,2]. Use the CALC/intersect to find the correct answer choice A.
An alternative solution converts the equations to exponential form: x = 5y and ![]() , or 5y= 2ey. Taking the natural log of both sides gives y ln5 = ln2 + y, and solving for y yields
, or 5y= 2ey. Taking the natural log of both sides gives y ln5 = ln2 + y, and solving for y yields ![]() . Finally substituting back to find x, 51.14
. Finally substituting back to find x, 51.14![]() 6.24. [1.4]
6.24. [1.4]
47. * (C) With your calculator in radian mode, plot the graphs of Y1 = sin x and Y2 = 5 cos x in a 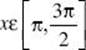 , and y
, and y![]() [–5,5] window. The solution is the x-coordinate of the point of intersection. An alternative solution is to divide both sides of the equation by cos x to get tan x = 5. Use your calculator to get tan–1 5 = 1.373. This is the first-quadrant solution, so add
[–5,5] window. The solution is the x-coordinate of the point of intersection. An alternative solution is to divide both sides of the equation by cos x to get tan x = 5. Use your calculator to get tan–1 5 = 1.373. This is the first-quadrant solution, so add ![]() . [1.3]
. [1.3]
48. * (B) With your calculator in polar mode, graph ![]() in a
in a ![]() and
and ![]() window. Let
window. Let ![]() run from 0 to 2
run from 0 to 2![]() in increments of 0.1. The graph of the function and the two axes form an isosceles right triangle of side length 1, so its area is 0.5.
in increments of 0.1. The graph of the function and the two axes form an isosceles right triangle of side length 1, so its area is 0.5.
An alternative solution is to multiply both sides of the equation by sin![]() + cos
+ cos![]() to get r sin
to get r sin![]() + r cos
+ r cos![]() = 1. Since x = r cos
= 1. Since x = r cos![]() and y = r sin
and y = r sin![]() , the rectangular form of the equation is x + y = 1. This line makes an isosceles right triangle of unit leg lengths with the axes, the area of which is
, the rectangular form of the equation is x + y = 1. This line makes an isosceles right triangle of unit leg lengths with the axes, the area of which is ![]()
49. * (B) The diagonal of the base is ![]() . The diagonal of the box is the hypotenuse of a right triangle with one leg
. The diagonal of the box is the hypotenuse of a right triangle with one leg ![]() and the other leg 5. Let
and the other leg 5. Let ![]() be the angle formed by the diagonal of the base and the diagonal of the box. Tan
be the angle formed by the diagonal of the base and the diagonal of the box. Tan ![]() , and so
, and so ![]() = tan–1 0.69337
= tan–1 0.69337![]() 35°. [1.3]
35°. [1.3]
50. * (C) Plot y = (2x + 1)2 in a window with x![]() [–2,2] and t
[–2,2] and t![]() [–1,5], and observe that choice C is the only possible choice.
[–1,5], and observe that choice C is the only possible choice.
An alternative solution is to note that the graph 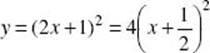 is a parabola with vertex at
is a parabola with vertex at ![]() that opens up. The only answer choice with these properties is C. [1.2]
that opens up. The only answer choice with these properties is C. [1.2]
Self-Evaluation Chart for Model Test 2

*Logic
|
|
|
Rating |
Number Right |
|
Excellent |
41–50 |
|
Very good |
33–40 |
|
Above average |
25–32 |
|
Average |
15–24 |
|
Below average |
Below 15 |
Calculating Your Score
Raw score R = number right – ![]() (number wrong), rounded = ______________
(number wrong), rounded = ______________
Approximate scaled score S = 800 – 10(44 – R) = ______________
If R ![]() 44, S = 800.
44, S = 800.