SAT SUBJECT TEST MATH LEVEL 2

PART 3

MODEL TESTS

Answer Sheet
MODEL TEST 3

Model Test 3

Tear out the preceding answer sheet. Decide which is the best choice by rounding your answer when appropriate. Blacken the corresponding space on the answer sheet. When finished, check your answers with those at the end of the test. For questions that you got wrong, note the sections containing the material that you must review. Also, if you do not fully understand how you arrived at some of the correct answers, you should review the appropriate sections. Finally, fill out the self-evaluation chart in order to pinpoint the topics that give you the most difficulty.

1. The slope of a line that is perpendicular to 3x + 2y = 7 is

 (A) –2

 (B)

 (C)

 (D)

 (E) 2

2. What is the remainder when 3x⁴ – 2x³ – 20x² – 12 is divided by x + 2?

 (A) –60

 (B) –36

 (C) –28

 (D) –6

 (E) –4

3. If , then

 (A) –3

 (B)

 (C) 0

 (D)

 (E) 3

4. If f(x) = 2 ln x + 3 and g(x) = e^x, then f(g(3)) =

 (A) 9

 (B) 11

 (C) 43.17

 (D) 47.13

 (E) 180.77

5. The domain of f(x) = log₁₀ (sin x) contains which of the following intervals?

 (A)

 (B)

 (C)

 (D)

 (E)

6. Which of the following is the ratio of the surface area of the sphere with radius r to its volume?

 (A)

 (B)

 (C)

 (D)

 (E)

7. If the two solutions of x²– 9x + c = 0 are complex conjugates, which of the following describes all possible values of c ?

 (A) c =0

 (B) c 0

 (C) c < 9

 (D)

 (E) c > 81

8. If tan x = 3, the numerical value of is

 (A) 0.32

 (B) 0.97

 (C) 1.03

 (D) 1.78

 (E) 3.16

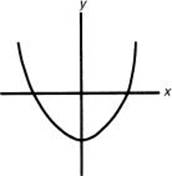
9. In the figure above, the graph of y = f(x) has two transformations performed on it. First it is rotated 180° about the origin, and then it is reflected about the x-axis. Which of the following is the equation of the resulting curve?

 (A) y = –f(x)

 (B) y = f(x + 2)

 (C) x = f(y)

 (D) y = f(x)

 (E) none of the above

10.

 (A) 0

 (B)

 (C) 1

 (D) 3

 (E)

11. The set of points (x, y, z) such that x = 5 is

 (A) a point

 (B) a line

 (C) a plane

 (D) a circle

 (E) a cube

12. The vertical distance between the minimum and maximum values of the function is

 (A) 1.414

 (B) 1.732

 (C) 2.094

 (D) 2.828

 (E) 3.464

13. If the domain of f(x) = –|x | + 2 is {x : –1 x 3}, f(x) has a minimum value when x equals

 (A) –1

 (B) 0

 (C) 1

 (D) 3

 (E) There is no minimum value.

14. What is the range of the function f(x) = x² – 14x + 43?

 (A) x 7

 (B) x 0

 (C) y –6

 (D) y –6

 (E) all real numbers

15. A positive rational root of the equation 4x³ – x² + 16x – 4 = 0 is

 (A)

 (B)

 (C)

 (D) 1

 (E) 2

16. The norm of vector is

 (A) 4.24

 (B) 3.61

 (C) 3.32

 (D) 2.45

 (E) 1.59

17. If five coins are flipped and all the different ways they could fall are listed, how many elements of this list will contain more than three heads?

 (A) 5

 (B) 6

 (C) 10

 (D) 16

 (E) 32

18. The seventh term of an arithmetic sequence is 5 and the twelfth term is –15. The first term of this sequence is

 (A) 28

 (B) 29

 (C) 30

 (D) 31

 (E) 32

19. The graph of the curve represented by is

 (A) a line

 (B) a hyperbola

 (C) an ellipse

 (D) a line segment

 (E) a portion of a hyperbola

20. Point (3,2) lies on the graph of the inverse of f(x) = 2x³ + x + A. The value of A is

 (A) –54

 (B) –15

 (C) 15

 (D) 18

 (E) 54

21. If f(x) = ax² + bx + c and f (1) = 3 and f (–1) = 3, then a + c equals

 (A) –3

 (B) 0

 (C) 2

 (D) 3

 (E) 6

22. In ABC, B = 42°, C = 30°, and AB = 100. The length of BC is

 (A) 47.6

 (B) 66.9

 (C) 133.8

 (D) 190.2

 (E) 193.7

23. If 4 sin x + 3 = 0 on 0 x < 2, then x =

 (A) –0.848

 (B) 0.848

 (C) 5.435

 (D) 0.848 or 5.435

 (E) 3.990 or 5.435

24. What is the sum of the infinite geometric series ?

 (A) 18

 (B) 36

 (C) 45

 (D) 60

 (E) There is no sum.

25. In a + bi form, the reciprocal of 2 + 6i is

 (A)

 (B)

 (C)

 (D)

 (E)

26. A central angle of two concentric circles is . The area of the large sector is twice the area of the small sector. What is the ratio of the lengths of the radii of the two circles?

 (A) 0.25:1

 (B) 0.50:1

 (C) 0.67:1

 (D) 0.71:1

 (E) 1:1

27. If the region bounded by the lines , x = 0, and y = 0 is rotated about the y-axis, the volume of the figure formed is

 (A) 18.8

 (B) 37.7

 (C) 56.5

 (D) 84.8

 (E) 113.1

28. If there are known to be 4 broken transistors in a box of 12, and 3 transistors are drawn at random, what is the probability that none of the 3 is broken?

 (A) 0.250

 (B) 0.255

 (C) 0.375

 (D) 0.556

 (E) 0.750

29. What is the domain of ?

 (A) x > 0

 (B) x > 2.47

 (C) –2.47 < x < 2.47

 (D) –3.87 < x < 3.87

 (E) all real numbers

30. Which of the following is a horizontal asymptote to the function f(x) = ?

 (A) y = –3.5

 (B) y = 0

 (C) y = 0.25

 (D) y = 0.75

 (E) y = 1.5

31. When a certain radioactive element decays, the amount at any time t can be calculated using the function , where a is the original amount and t is the elapsed time in years. How many years would it take for an initial amount of 250 milligrams of this element to decay to 100 milligrams?

 (A) 125 years

 (B) 200 years

 (C) 458 years

 (D) 496 years

 (E) 552 years

32. If n is an integer, what is the remainder when 3x^{(2n+ 3)} – 4x^{(2n + 2)} + 5x^{(2n+ 1)} – 8 is divided by x + 1?

 (A) –20

 (B) –10

 (C) –4

 (D) 0

 (E) The remainder cannot be determined.

33. Four men, A, B, C, and D, line up in a row. What is the probability that man A is at either end of the row?

 (A)

 (B)

 (C)

 (D)

 (E)

34.

 (A) 260

 (B) 50

 (C) 40

 (D) 5

 (E) none of these

35. The graph of y⁴ – 3x² + 7 = 0 is symmetric with respect to which of the following?

  I. the x -axis

 II. the y-axis

 III. the origin

 (A) only I

 (B) only II

 (C) only III

 (D) only I and II

 (E) I, II, and III

36. In a group of 30 students, 20 take French, 15 take Spanish, and 5 take neither language. How many students take both French and Spanish?

 (A) 0

 (B) 5

 (C) 10

 (D) 15

 (E) 20

37. If f(x) = x², then

 (A) 0

 (B) h

 (C) 2x

 (D) 2x + h

 (E)

38. The plane whose equation is 5x + 6y + 10z = 30 forms a pyramid in the first octant with the coordinate planes. Its volume is

 (A) 15

 (B) 21

 (C) 30

 (D) 36

 (E) 45

39. What is the range of the function ?

 (A) All real numbers

 (B) All real numbers except 5

 (C) All real numbers except 0

 (D) All real numbers except −1

 (E) All real numbers greater than 5

40. Given the set of data 1, 1, 2, 2, 2, 3, 3, x, y, where x and y represent two different integers. If the mode is 2, which of the following statements must be true?

 (A) If x = 1 or 3, then y must = 2.

 (B) Both x and y must be > 3.

 (C) Either x or y must = 2.

 (D) It does not matter what values x and y have.

 (E) Either x or y must = 3, and the other must = 1.

41. If and g(x)=x², for what value(s) of x does f(g(x)) = g(f(x))?

 (A) –0.55

 (B) 0.46

 (C) 5.45

 (D) –0.55 and 5.45

 (E) 0.46 and 6.46

42. If 3x – x² 2 and y² + y 2, then

 (A) –1 xy 2

 (B) –2 xy 2

 (C) –4 xy 4

 (D) –4 xy 2

 (E) xy = 1, 2, or 4 only

43. In ABC, if sin A = and sin B = , sin C =

 (A) 0.14

 (B) 0.54

 (C) 0.56

 (D) 3.15

 (E) 2.51

44. The solution set of is

 (A) 0 < x <

 (B) x <

 (C) x >

 (D) < x < 1

 (E) x > 0

45. Suppose the graph of f(x) = –x³ + 2 is translated 2 units right and 3 units down. If the result is the graph of y = g(x), what is the value of g (–1.2)?

 (A) –33.77

 (B) –1.51

 (C) –0.49

 (D) 31.77

 (E) 37.77

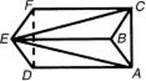
46. In the figure above, the bases, ABC and DEF, of the right prism are equilateral triangles of side s. The altitude of the prism BE is h. If a plane cuts the figure through points A, C, and E, two solids, EABC, and EACFD, are formed. What is the ratio of the volume of EABC to the volume ofEACFD?

 (A)

 (B)

 (C)

 (D)

 (E)

47. A new machine can produce x widgets in y minutes, while an older one produces u widgets in w hours. If the two machines work together, how many widgets can they produce in t hours?

 (A)

 (B)

 (C)

 (D)

 (E)

48. The length of the major axis of the ellipse 3x² + 2y² – 6x + 8y – 1 = 0 is

 (A)

 (B)

 (C)

 (D) 4

 (E)

49. A recent survey reported that 60 percent of the students at a high school are girls and 65 percent of girls at this high school play a sport. If a student at this high school were selected at random, what is the probability that the student is a girl who plays a sport?

 (A) 0.10

 (B) 0.21

 (C) 0.32

 (D) 0.39

 (E) 0.42

50. If x – 7 divides x³ – 3k³x² – 13x – 7, then k =

 (A) 1.19

 (B) 1.34

 (C) 1.72

 (D) 4.63

 (E) 5.04

If there is still time remaining, you may review your answers.

Answer Key
MODEL TEST 3

ANSWERS EXPLAINED

The following explanations are keyed to the review portions of this book. The number in brackets after each explanation indicates the appropriate section in the Review of Major Topics (Part 2). If a problem can be solved using algebraic techniques alone, [algebra] appears after the explanation, and no reference is given for that problem in the Self-Evaluation Chart at the end of the test.

An asterisk appears next to those solutions in which a graphing calculator is necessary.

1. (C) Transform the given equation into slope-intercept form: to see that the slope is – . The slope of a perpendicular line is the negative reciprocal, or . [1.2]

2. * (C) Let f(x) = 3x⁴ – 2x³ – 20x² – 12 and recall that f(–2) is equal to the remainder upon division of f(x) by x + 2. Enter f(x) into Y₁, return to the Home Screen, and enter Y₁(–2) to get the correct answer choice.

An alternative solution is to use synthetic division to find the remainder.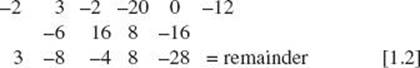

3. (C) Solve the equation by adding to both sides and getting or , so x = 1. Therefore, . [algebra]

4. (A) Since g(3) = e³, f (g(3)) = 2 ln e³ + 3. ln e³ = 3. So f(g(3)) = 6 + 3 = 9. [1.4]

5. (C) Since the domain of log₁₀ is positive numbers, then the domain of f consists of values of x for which sin x is positive. This is only true for 0 < x < . [1.3]

6. (B)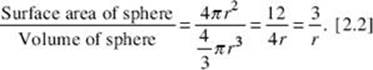

7. * (D) Plot the graph of y = x² – 9x in the standard window and observe that you must extend the window in the negative y direction to capture the vertex of the parabola. Since this vertex must lie above the x-axis for the solutions to be complex conjugates, c must be bigger than |minimum| = 20.25 = . (The minimum is found using CALC/minimum.)

An alternative solution is to use the fact that for the solutions to be complex conjugates, the discriminant b² – 4ac = 81 – 4c < 0, or c > . [1.2]

8. * (C) Since tan x = 3, x could be in the first or third quadrants. Since, however, is only defined when csc x 0, we need only consider x in the first quadrant. Thus, we can enter to get the correct answer choice C. [1.3]

9. (D) The two transformations put the graph right back where it started. [2.1]

10. * (E) Enter (3x³ – 7x²⁺²)/(4x² –3x – 1) into Y₁. Enter TBLSET and set TblStart = 110 and Tbl = 10. Then enter TABLE and scroll down to larger and larger x values until you are convinced that Y₁ grows without bound.

An alternative solution is to divide the numerator and denominator by x³ and then let x . The numerator approaches 3 while the denominator approaches 0, so the whole fraction grows without bound. [1.2]

11. (C) Since the y- and z-coordinates can have any values, the equation x = 5 is a plane where all points have an x-coordinate of 5. [2.2]

12. * (A) Plot the graph of using Ztrig. The minimum value of the function is clearly zero, and you can use CALC/maximum to establish 1.414 as the maximum value.

This function inside the absolute value is sinusoidal with amplitude . The absolute value eliminates the bottom portion of the sinusoid, so this is the vertical distance between the maximum and the minimum as well. [1.3]

13. * (D) Plot the graph of y = –|x| + 2 on an and window. Examine the graph to see that its minimum value is achieved when x = 3.

An alternative solution is to realize that y is smallest when x is largest because of the negative absolute value. [1.6]

14. * (D) Plot the graph of y = x² – 14x + 43, and find its minimum value of –6. All values of y greater than or equal to –6 are in the range of f . [1.1]

15. * (A) Plot the graph of y = 4x³ – x² + 16x – 4 in the standard window and zoom in once to get a clearer picture of the location of the zero. Use CALC/zero to determine that the zero is at x = 0.25.

An alternative solution is to use the Rational Roots Theorem to determine that the only possible rational roots are . Synthetic division with these values in turn eventually will yield the correct answer choice.

Another alternative solution is to observe that the left side of the equation can be factored: 4x³ – x² + 16x – 4 = x²(4x – 1) + 4(4x – 1) = (4x – 1)(x² + 1) = 0. Since x² + 1 can never equal zero, the only solution is

16. * (C)

17. * (B) “More than 3” implies 4 or 5, and so the number of elements is . [3.1]

18. (B) There are 5 common differences, d, between the seventh and twelfth terms, so 5d = –15 – 5 = –20, and d = –4. The seventh term is the first term plus 6d, so 5 = t₁ – 24, and t₁ = 29. [3.4]

19. * (E) In parametric mode, plot the graph of x = sec t