SAT Math 1 & 2 Subject Tests

Chapter 12

Drills: Answers and Explanations

Chapter 3: Arithmetic

Prime factors

1 64 = 2 × 2 × 2 × 2 × 2 × 2

2 70 = 2 × 5 × 7

3 18 = 2 × 3 × 3

4 98 = 2 × 7 × 7

5 68 = 2 × 2 × 17

6 51 = 3 × 17

Factors

3 B 21 can also be written as 3 × 7, and 18 as 2 × 3 × 3. The smallest number that contains both is 2 × 3 × 3 × 7, or 126.

7 E 53 is a prime number; its largest prime factor is 53. None of the other answers contains so large a prime factor. (A) is (2)(5)(17), so its greatest prime factor is 17. (B) is (3)(3)(13), so its greatest prime factor is 13. (C) is (2)(2)(2)(11), so its greatest prime factor is 11. (D) is (2)(31), so its greatest prime factor is 31.

9 C The smallest integer divisible by 10 and 32 is 160, and the smallest integer divisible by 6 and 20 is 60. The difference between them is 100. Remember to factor each time as shown in number 3, above.

Even and odd, positive and negative

15 A Let”s start with I. We know from our rules that an odd number times an odd number is an odd number. So I has to be true. Use POE to eliminate (B). Now let”s skip down to III for a moment. We know from I that odd times odd equals odd. We also know that odd plus odd is even. And an even times an even is even. So III will be an even number. Since III isn”t true, eliminate (D) and (E). Let”s look at II. Remember that the question asks which of the following must be an odd integer. Since an odd integer divided by an odd integer isn”t always an integer, you can eliminate (C). If you ever forget a rule, you can always try a couple of numbers.

18 D The statement cd < 0 means that one of the numbers is positive and one negative; that”s the only way to get a negative product. Try your own numbers to eliminate answer choices. If you try c = 1 and d = −3, only (A) and (D) are true. Switch them and try c = −3 and d = 1, and only (D) remains true.

20 C Use your rules. Choice (A) would be an even times an odd, which is even. Choice (B) would be an odd times an even (even result), plus an even, squared, which would remain even. Choice (C) would be even minus one, which results in an odd number. Choice (D) would be an odd plus an even, which is odd, and (E) would be an odd divided by an even, which may not be an integer. So we”re down to (C) and (D). Since y is negative, it is possible that (D) would yield a negative number. The answer must be (C). Again, you can always try out sample numbers to prove the rules.

PEMDAS and your calculator

1 5

2 35

3 12

4 35

5 0

Word-problem translation

1 6.5 = • 260; x = 2.5

2 20 = • 180; n = 11

3  • • 25 = x; x = 3

4 x = 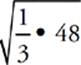; x = 4

5  = • y; y = y²; = ; y = 64

Percent change

2 B You already know that the difference is going to be 25. Set up your formula: • 100 = 16.67. So, adding 25 gallons to 150 gallons is a 16.67% increase.

5 B The decrease from 5 to 4 is a 20% decrease, and the increase from 4 to 5 is a 25% increase. So the difference is 5%.

12 C Using the formula 12 = (150 ÷ x)100, you get x = 1,250, so 1,250 must have been the original amount. 1,250 + 150 = 1,400. Be careful to read “after the deposit” in the question.

Repeated percent change

35 D Using the formula, you get 1,000(1.05¹²) = 1,795.856.

40 E For this question, you need to compute 100 annual increases of 8%, so you must multiply the starting amount, 120,000, by 1.08¹⁰⁰, which gives you 263,971,350.8—which can also be written as 2.6 × 10⁸. If you weren”t sure, multiply the answers in your calculator to check your work.

43 C This question is a little trickier. For each annual decrease of 4%, you must multiply by 0.96. The easiest way to solve the question is to start with 2,000 and keep multiplying until the result is less than 1,000—just count the number of decreases it takes. The seventeenth annual decrease makes it less than 1,000, so the sixteenth is the last one that is not less than 1,000—and 1995 + 16 = 2011. You can also use logs, which we”ll get to in a little while.

Averages

1 There were 9 people at dinner.

2 All told, 4,500 apples were picked.

3 The average height of a chess club member is 5.5 feet.

Multiple-average questions

33 D Nineteen donations averaging $485 total $9,215. Twenty donations averaging $500 total $10,000. The difference is $785.

35 A The Tribune received 80 letters in the first 20 days and 70 for the last 10 days. That”s a total of 150 in 30 days, or 150 ÷ 30 = 5 letters per day on average.

36 A One day in five out of a year is 73 days. At 12 a day, that”s 876 umbrellas sold on rainy days. The rest of the year (292 days) is clear. At 3 umbrellas a day, that”s another 876 umbrellas. A total of 1,752 umbrellas in 365 days makes a daily average of 4.8 umbrellas.

Exponents

1 b = 3 (1 root)

2 x = 11, −11 (2 roots)

3 n = 2 (1 root)

4 c = , − (2 roots)

5 x = 3, −3 (2 roots)

6 x = −2 (1 root)

7 d = 3, −3 (2 roots)

8 n = any real number; everything to the 0 power is 1.

1 C Remember that the top is the exponent and the bottom is the root. So in your calculator, put in 4^(3/2). This is the same as cubing 4 and then taking the square root of your result (or taking the square root of 4 and then cubing that result). Any way you slice it, the answer is 8.

2 D Remember your rules. A negative exponent means flip it. And a fractional exponent means the top is the exponent and the bottom is the root. You may have ended up with 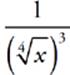, which isn”t wrong. It just happens to not be in the answers. The only correct answer is .

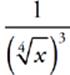3 A Flip and square it: 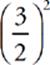= 2.25. Don”t forget your parentheses in your calculator.

4 E Flip and take the third root.

5 A In your calculator it goes, either as is (with parentheses) or if you need to take more steps, just remember that the numerator is the exponent and the denominator is the root. Or notice that must be less than and use POE.

6 D What”s anything raised to the zero power? That”s right, 1.

Chapter 4: Algebra

Solving equations

1 x = {5, −5}
If you”re having trouble, think of peeling away the layers of the left side until you get to just x. So you”re going to multiply by 17, then add 7, then divide by 3, then take the square root of both sides. Remember: When you take the square root of both sides, you”ll end up with two answers: positive and negative.

2 n = {0, 5}
This is tricky. You most likely found that the answer is 5. Remember: You can divide both sides by n only if n isn”t 0. So you also have to consider that n could be 0. In this case, it can.

3 a = 0.75
Peel away those layers.

4 s = 12
Keep peeling.

5 x = 0.875
Make sure you didn”t cancel the 5”s. You can cancel only when numbers are being multiplied or divided, not added or subtracted. Did you get ? Same thing!

6 m = 9 or m = −14
Because the left side of the equation is inside absolute value signs, you know it can be either positive or negative. So set up two equations! In the first equation, set 2m + 5 equal to 23. In the second equation, set 2m + 5 equal to −23. Then solve each equation for m. These are your two possible values for m.

7 r = 27 or r = −13
Set this problem up just like question 6, above. The value inside the absolute value signs can be either positive or negative, so write an equation for each scenario. Solve each equation to come up with the two possible values for r.

Factoring and distributing

3 D This equation can be rearranged to look like: 50x(11 + 29) = 4,000. This is done simply by factoring out 50 and x. Once you”ve done that, you can add 11 and 29 to produce 50x(40) = 2,000x = 4,000. Therefore, x = 2.

17 E Here, distributing makes your math easier. Distributing −3b into the expression (a + 2) on top of the fraction gives you 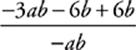, which simplifies to , which equals 3.

36 B The trap in this question is to try to cancel similar terms on the top and bottom—but that”s not possible, because these terms are being added together, and you can cancel only in multiplication. Instead, factor out x² on top of the fraction. That gives you 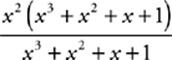. The whole mess in parentheses cancels out (now that it”s being multiplied), and the answer is x².

Plugging In

5 E Let”s make p = 20, t = 10, and n = 3. That”s 3 items for $20.00 each with 10% tax. Each item would then cost $22.00, and three could cost $66.00. Only answer choice (E) equals $66.00.

8 C Let”s make x = 5, a = 2, b = 3. That means Vehicle A travels at 5 mph for 5 hours, or 25 miles. Vehicle B travels at 7 mph for 8 hours, or 56 miles. That”s a difference of 31 miles. Only (C) equals 31.

17 C Let”s make n = 3, then 5 − 3 = 2 and 3 − 5 = −2. These numbers have the same absolute value, so the difference between them is zero.

20 B Let”s Plug In a = 10, b = 1, m = 4. That means that Company A builds 10 skateboards a week and 40 skateboards in 4 weeks. Company B builds 7 skateboards in a week (1 per day), or 28 in 4 weeks. That”s a difference of 12 between the two companies. Only (B) equals 12 when you Plug In a = 10, b = 1, m = 4.

23 E Plug In a = 4 and b = 2. Okay, all three fail. Let”s try some different-sized numbers like a = 10 and b = 2. Now I works; eliminate (B) and (D). Let”s try to make a + b small; Plug In a = 4 and b = −4. Now II and III work; eliminate (A) and (C).

30 A Plug In x = 2 and y = 3. Oh well—they all work! Try x = −3 and y = −2. Now II fails; eliminate (C), (D), and (E). III also fails; eliminate (B).

Plugging In The Answers (PITA)

11 D The answer choices represent Michael”s hats. Start with answer (C): If Michael has 12 hats, then Matt has 6 hats and Aaron has 2. That adds up to 20, not 24—you need more hats, so move on to the next bigger answer, (D). Michael now has 14 hats, meaning Matt has 7 and Aaron has 3. That adds up to 24, so you”re done.

17 D There”s a little shortcut you can take if you remember the average pie. Since the total is 3,200 and you have two parts, you know that the average will be 1,600. This means that the difference will be 800. Work through the answer choices, starting with (C). A ratio of 2:5 has 7 parts. Divide 3,200 by 7. Each part would be 457.14—it doesn”t work out with whole numbers, so it can”t be right. Then move on to (D); a ratio of 3:5 has 8 parts, each of which would be 400. That means the shipment is divided into shares of 1,200 and 2,000. Their difference is 800, and their average is 1,600, which is what we”re looking for!

27 D Start with (C); if the largest of the three integers is 5, then the total of the other two integers would have to be 15 − 5 or 10. No two numbers less than 5 have a sum of 10, so eliminate (A), (B), and (C). If you Plug In (D), 9 is the largest number. For the product of all three integers to be 45, the product of the other two integers must be 5. So these two integers can only be 5 and 1. Now we find the sum of all three numbers. 9 + 5 + 1 = 15, so (D) is the correct answer.

Inequalities

1 n ≥ 3

2 r < 7

3 x ≥ −

4 x <

5 t ≤ 3

6 n ≤ 4

7 p >

8 s ≥ 1

9 x ≥ −7

10 s ≥

Working with ranges

1 −8 < −x < 5

2 −20 < 4x < 32

3 1 < (x + 6) < 14

4 7 > (2 − x) > −6

5 −2.5 < < 4

Working with ranges

1 −4 ≤ b − a ≤ 11

2 −2 ≤ x + y ≤ 17

3 0 ≤ n² ≤ 64

4 3 < x − y < 14

5 −13 ≤ r + s ≤ 13

6 −126 < cd < 0

7 −1 ≤ 7
Because the absolute value is less than 4, whatever”s inside the absolute value must be between −4 and 4. Therefore, −4 ≤ 3 − x ≤ 4. Start solving this by subtracting 3 from all three sides: −7 ≤ −x ≤ 1. Then divide through by −1 (remember to flip the direction of the inequality signs because you”re dividing by a negative number): 7 ≥ x ≥ −1.

8 a ≤ −10 or a ≥ 3
Because the absolute value is greater than 13, the stuff inside the absolute value must be either less than −13 or greater than 13. Therefore, you have two inequalities: 2a + 7 ≤ −13 or 2a + 7 ≥ 13. Solve each inequality separately.

Direct and inverse variation

15 C There are variables in the answers, so Plug In! Quantities in inverse variation always have the same product. That means that ab = 3 • 5, or 15, always. Plug In a number for x, such as 10. Now set up your proportion: 3 • 5 = a • 10. So 10a = 15, and a = 2.5. Plug x = 10 into the answers and find the answer choice that gives you 2.5. Only (C) does.

18 D Remember your formulas. Direct means divide. Quantities in direct variation always have the same proportion. In this case, that means that = . When m = 5, solve the equation = . Multiply both sides by 5 and you”ll find that n = 6.25.

24 A Direct variation means the proportion is constant, so that = . To find the value of p when q = 1, solve the equation = ; p must be 0.3.

26 B Remember that direct means divide. Set up your proportion: 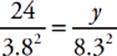. If you simplify this, you get 120.77, which is (B). Be careful. If you answered (E), you forgot that the direct variation was between y and x², not y and x.

Work and travel questions

11 C The important thing to remember here is that when two things or people work together, their work rates are added up. Pump 1 can fill 12 tanks in 12 hours, and Pump 2 can fill 11 tanks in 12 hours. That means that together, they could fill 23 tanks in 12 hours. To find the work they would do in 1 hour, just divide 23 by 12. You get 1.91666….

12 A To translate feet per second to miles per hour, take it one step at a time. First, find the feet per hour by multiplying 227 feet per second by the number of seconds in an hour (3,600). You find that the projectile travels at a speed of 817,200 feet per hour. Then divide by 5,280 to find out how many miles that is. You get 154.772.

18 B The train travels a total of 400 miles (round-trip) in 5.5 hours. Now that you know distance and time, plug them into the formula and solve to find the rate. 400 = r × 5.5, so r = 72.73.

25 D Plug In! Say Jules can make 3 muffins in 5 minutes (m = 3, s = 5). Say Alice can make 4 muffins in 6 minutes (n = 4, t = 6). That means that Jules can make 18 muffins in 30 minutes, and Alice can make 20 muffins in 30 minutes. Together, they make 38 muffins in 30 minutes. That”s your target number. Take the numbers you plugged in to the answers and find the one that gives you 38. Answer choice (D) does the trick.

Average speed

19 D Find the total distance and total time. The round-trip distance is 12 miles. It takes hour to jog 6 miles at 12 mph, and hour to jog back at 9 mph, for a total of 1 hours. Do the division, and you get 10.2857 mph.

24 D This one is easier than it looks. Fifty miles in 50 minutes is a mile a minute, or 60 mph. Forty miles in 40 minutes is also 60 mph. The whole trip is made at one speed, 60 mph.

33 B Plug In an easy number for the unknown distance, like 50 miles. It takes 2 hours to travel 50 miles at 25 mph, and 1 hour to return across 50 miles at 50 mph. That”s a total distance of 100 miles in 3 hours, for an average speed of 33 mph. (A) and (E) are Joe Bloggs answers.

Simultaneous equations

26 C Here, you want to make all of the b terms cancel out. Add the two equations, and you get 5a = 20, so a = 4.

31 D Here, you need to get x and y terms with the same coefficient. If you subtract the second equation from the first, you get 10x − 10y = 10, so x − y = 1.

34 D The question is solvable as the example on the previous page was, by multiplication. Multiplying all three equations together gives you a²b²c² = 2.25. Don”t pick (B)! Take the positive square root of both sides, and you get abc = 1.5.

37 E Here, you need to get rid of the z term and cancel out a y. The way to do it is to divide the first equation by the second one, = . The z and a y cancel out, and you”re left with = , or 0.8. Even though there are more variables than equations, ETS questions almost always have a trick to let you solve them the easy way.

FOIL

1 x² + 9x − 22

2 b² + 12b + 35

3 x² − 12x + 27

4 2x² − 3x − 5

5 n³ − 3n² + 5n − 15

6 6a² − 11a − 35

7 x² − 9x + 18

8 c² + 7c − 18

9 d² + 4d − 5

Factoring quadratics

1 a = {1, 2} Factor to (a − 1)(a − 2) = 0.

2 d = {−7, −1} Factor to (d + 7)(d + 1) = 0.

3 x = {−7, 3} Factor to (x + 7)(x − 3) = 0.

4 x = {−5, 2} Factor to 3(x² + 3x − 10) = 3(x + 5)(x − 2) = 0.

5 x = {−11, −9} Factor to 2(x² + 20x + 99) = 2(x + 11)(x + 9) = 0.

6 p = {−13, 3} Factor to (p + 13)(p − 3) = 0. Subtract 39 from both sides first.

7 c = {−5, −4} Factor to (c + 5)(c + 4) = 0.

8 s = {−6, 2} Factor to (s + 6)(s − 2) = 0.

9 x = {−1, 4} Factor to (x + 1)(x − 4) = 0.

10 Factor the expression (n² − 5)(n² + 2) = 0. So n² = 5 or −2. But n² is never negative, so n = ±.

Special quadratic identities

17 A Remember that n² − m² = (n − m)(n + m). So fill in what you know and solve for what you don”t: 24 = (−3)(n + m). You don”t need to find each variable individually.

19 B Remember that (x + y)² = x² + 2xy + y². Again you have all the parts except for what the question is asking for: 3² = 8 + 2xy. So 2xy = 1 and xy = 0.5.

24 D Translate into math. You know that x + y = 9 and x² + y² = 36. It”s asking for xy. The pieces that the question gives you relate to (x + y)² = x² + 2xy + y². So, 9² = 36 + 2xy; 2xy = 45; and xy = 22.5. Notice that (E) is a partial answer.

The quadratic formula

1 2 distinct real roots; x = {0.81, 6.19}

2 no real roots (2 imaginary roots)

3 2 distinct real roots; s = {0.76, 5.24}

4 2 distinct real roots; x = {−1.41, 1.41}

5 1 real root; n = −2.5 (2 identical real roots, that is, a “double root”)

Chapter 5: Plane Geometry

Basic rules of lines and angles

1 x = 50°; y = 130°; z = 130°; a = 50°; b = 130°; c = 50°

2 x = 105°; y = 75°

3 a = 120°; b = 60°; c = 120°; d = 60°; e = 120°; f = 60°

8 B When parallel lines are crossed by a third line, any small angle plus any big angle equals 180°.

13 E Plug In! Remember that where the line intersects the parallel sides of the rectangle, any small angle plus any big angle is 180°. Plug In, for example, 80° for the smaller angles s and v, and 100° for the larger angles, t and u. The angles r and w must measure 90° each. Once you”ve plugged in these values you”ll quickly see that only (E) must be equivalent to angle t.

16 E Fred”s theorem tells you that the sum of ∠DBC and ∠BDE is 180°. You don”t, however, know anything about the difference between them. Plugging In various numbers should soon convince you that the difference cannot be determined. Remember Joe Bloggs though, and steer away from such enticing or easy-way-out answers as the question numbers get higher.

Third side rule

12 E The length of the unknown side, ST, must be between the sum and difference of the other two lengths—that is, between 3 and 19. Add the sides and that makes the perimeter anywhere between 22 and 38. Notice that (A) answers the wrong question.

17 A Since the triangle is isosceles, the unknown side must be either 5 or 11. But a 5-5-11 triangle violates the Third Side Rule—it”s not possible. That leaves only 11 as a possible value of the missing side.

18 E This is just another application of the Third Side Rule. The third distance must be between 2 and 10. Only (E) violates the rule.

The Pythagorean theorem

1 x = , or 9.4334

2 n = , or 9.2195

3 a = , or 3.8730

4 d = = 5, or 7.0710

5 x = 7

6 r = , or 12.0416

Area of triangles

9 E Write out the formula for the area of a triangle, using the lengths the question has given: ab. You know that the area is 3b. So, ab = 3b. Now, solve for a. a = 3 and a = 6.

15 A Both triangles have the same height, and if their areas are equal, they must have the same base as well. Since triangle OAD has a base of 8, triangle ABC must also have a base of 8.

37 B Notice that the area of ABC can be computed two different ways; with AC as the base or with BC as the base. Either way, the base and height must multiply to the same number, because a triangle can have only one area. That means that 12 times BE must equal 9 times 10: 12BE = 90, and BE = 7.5.

38 C If the perimeter of an equilateral triangle is 24, then each side has a length of 8. Plug that into the formula for the area of an equilateral triangle, and you get 27.71.

44 D Just set the formula for the area of an equilateral triangle equal to 12, and solve for s. You get 5.26. The perimeter is 3s, or 15.79. (A) is a Joe Bloggs answer, because he sees a number in the answers that reminds him of the question and he is tempted to pick familiar numbers.

46 D You”re given two sides of a triangle and the angle between them, and you”re supposed to find the area. Use the formula A = ab sin θ. In this case, A = (6.4)(10.8)(sin 55°) = 28.31. (E) is a Joe Bloggs answer (A = bh).

Pythagorean triplets

1 x = 9

2 d = 26

3 n = 0.5

The 45°-45°-90° triangle

1 x = 3, or 8.485

2 n = 1.5, or 2.121

3 s = 7, so s = . This is equivalent to s = , or 4.950

The 30°-60°-90° triangle

1 x = 3, or 5.196

2 n = , or 2.887

3 d = 4, or 6.928

Right triangles

7 A With the Pythagorean Theorem, you could compute the missing length of the longest side. There”s only one possible perimeter. Notice that you don”t even have to know what it is in order to answer the question correctly. Don”t waste time computing! (The hypotenuse turns out to be 11.4, in case you”re curious.)

13 E You can”t use the Pythagorean theorem unless you know which side of a right triangle is the hypotenuse. Since you don”t know whether 8 or the unknown side is the hypotenuse, it”s impossible to know the length of the missing side.

16 C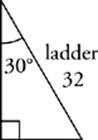

Draw it! You”ll find that the floor, wall, and ladder form a 30°-60°-90° triangle. The ladder itself is the hypotenuse, so the hypotenuse is 32. Because the 30° angle is against the wall, the short leg is the ground. So the short leg is 16 and the other leg, or the wall, is 16 or 27.71, which is (C).

19 B An isosceles right triangle must be a 45°-45°-90° triangle, with sides x, x, and x. Since the perimeter equals 23.9, that means 2x + x = 23.9. In order to solve, factor out an x and isolate x. This tells you that x = 7, and you can plug this value into the equation for the area of the triangle, or x². The area of the triangle is 24.5.

Similar triangles

1 a = 4; b = 6.92; x = 2; y = 1.73

2 a = 5; s = 15

3 c = 11; m = 12.25

37 A These triangles are similar because they have identical angles. If one length of triangle ABC is half of a corresponding length of triangle FGH, that means that all of the lengths in ABC will be half the corresponding lengths in FGH. The easiest way to solve the problem is by Plugging In a base and height for FGH that would yield an area of 0.5; a base of 1 and a height of 1 would be the easiest. Then just Plug In the corresponding dimensions of ABC, making sure that they”re half of the dimensions in triangle FGH: The base is and the height is . The area comes out to , or 0.125, which rounds to 0.13.

40 C This question is much like question 37, except that you have more freedom to Plug In numbers. Once again, the triangles are similar; Fred”s theorem tells you that they have identical angles. Then just Plug In easy numbers. Suppose AD = 4; from the problem, DB = 2, so AB = 6. This shows you that the lengths of the smaller triangle are the lengths of the larger. Suppose AE = 6, then AC = 9. The area of triangle ADE is then 12, while the area of triangle ABC is 27. reduces to .

45 A Use the Pythagorean theorem to complete the dimensions of triangle LMN. It has sides of length 4, , and 8. If you simplify , you”ll find it”s equal to 4. That makes the lengths 4, 4, and 8, which should look familiar. It”s a 30°-60°-90° triangle. (You could still figure it out if you didn”t notice that it”s a 30°-60°-90° triangle.) Since a right triangle divided by an altitude from its right angle forms three similar triangles, the little triangle LPN must also be a 30°-60°-90° triangle. If its hypotenuse has a length of 4, then its legs have lengths of 2 and 2. Those legs are the base and height of triangle LPN. Use them to calculate the triangle”s area, and you get 3.464.

Quadrilaterals

22 A Use the cool formula for the area of a square.

34 D Drawing a height down from K gives you a 30°-60°-90° triangle with hypotenuse 6. So the height is 3 or 5.196. Multiplying the base by the height gives you (D). For Math Level 2, you can use the nifty A = ab sin θ formula. So A = (6)(10)(sin 60°). (E) is a Joe Bloggs answer (10 × 6 = 60).

40 B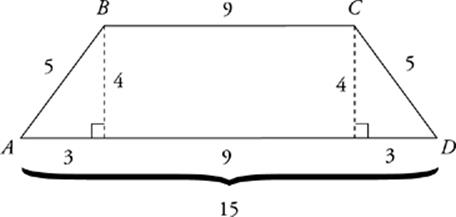

AD is 9 + 6 = 15. If the perimeter is 34, then AB = 5, making this an isosceles trapezoid. If you draw the heights down from B and C, they will each cut off a right triangle with a base of 3 (half of the 6 you”re told about). These are 3-4-5 right triangles, so the height of the trapezoid is 4. Now you can either plug 9, 15, and 4 into the trapezoid area formula, or you can find the sum of the areas of the two right triangles and the rectangle between them. (A) is a Joe Bloggs answer (9 × 5 = 45).

45 B Each diagonal cuts the rectangle into two 30°-60°-90° triangles, with the diagonal as hypotenuse. That makes the base and height of the rectangle the x and x legs of the triangle. If x : x = 62.35, then x = 6.0, and the hypotenuse of the triangle (2x) has a length of 12.0. The sum of the two diagonals is 24.0.

Circles

1 C = 8π; A = 16π

2 C = 15.85; r = 2.52 Divide the area (20), which is pr², by p and take the square root of the result to solve for r.

3 A = 5.09; r = 1.27

More circles

12 D Remember that a sector of a circle takes equal portions of angle, circumference, and area. The circle”s circumference is 6π or 18.85. Because 4.71 ÷ 18.85 is about 1/4, the sector also takes up one-fourth of 360°, or 90°.

29 A Draw a line from B to O to make two shapes. The shaded region is a quarter-circle plus a 45°-45°-90° triangle. The triangle has an area of , or 12.5. The quarter-circle has an area of 19.63. They add up to 32.13.

31 B As in most shaded-area problems, the trick is to subtract one shape from another to get the shaded region itself. Here, you need to subtract the hexagon”s area from that of the circle. To compute the area of the hexagon, divide it into 6 equilateral triangles, each with a side of 4—use the equilateral triangle formula to find their areas. Then subtract the hexagon”s area (41.57) from the circle”s area (50.27) to get the answer, 8.7.

43 C You know that both OA and OC are 2, since they”re both radii. The question says that OA = AC, which means that AC is also 2. Because triangle OAC is equilateral, all of its angles measure 60°. The radius OA must be perpendicular to line l, making a 90° angle; that makes triangleOAC a 30°-60°-90° triangle. The length of AB is 2, or 3.46.

45 A Take one statement at a time. I must be true, since BC is the hypotenuse of a right triangle, and must be longer than the triangle”s legs. Because point A could fall anywhere on the left half of the circumference, choice II could be true, but doesn”t have to be; and III is impossible, since land m must be parallel.

Chapter 6: Solid Geometry

Triangles in rectangular solids

32 D Use the formula for the long diagonal of a cube. Given that the cube”s edge is the cube root of 27, or 3, the formula will be 3² + 3² + 3² = d². If you simplify this, you”ll see that the cube”s long diagonal must be 5.2.

36 E Be careful here; you won”t be using the Super Pythagorean theorem. The sides of this triangle are the diagonals of three of the solid”s faces. BD is the hypotenuse of a 3-4-5 triangle, and BE is the hypotenuse of a 5-12-13 triangle. For DE, use the Pythagorean theorem with a = 3 and b= 12: DE = = 12.37. The sum of the three sides is 5 + 13 + 12.37 = 30.37.

39 A This is a long-diagonal question, with a twist. Each edge of the cube is 1, but you”re actually finding the long diagonal of a quarter of the cube. Think of it as finding the long diagonal of a rectangular solid with dimensions 1 • • . Plug those three numbers into the Super Pythagorean theorem. You could also solve this by finding the length of CN and then using the Pythagorean theorem on triangle MCN.

Volume

17 D PITA! Quickly move through the answer choices (starting in this case with the smallest, easiest numbers), calculating the volumes and surface areas of each. The only answer choice that makes these quantities equal is (D).

24 E This one”s a pain. The only way to do it is to try out the various possibilities. The edges of the solid must be three factors which multiply to 30, such as 2, 3, and 5. That solid would have a surface area of 62. The solid could also have dimensions of 1, 5, and 6, which would give it a surface area of 82. Keep experimenting, and you find that the solid with the greatest surface area has the dimensions 1, 1, and 30, giving it a surface area of 122.

28 C So you don”t know the formula for the area of a pentagon? You don”t need to. Just use the formula for the volume of a prism, V = Bh.

43 B The sphere has a volume of 4.19. When submerged, it will push up a layer of water having equal volume. The volume of this layer of water is the product of the area of the circular surface (50.27) and the height to which it”s lifted—it”s like calculating the volume of a very flat cylinder. You get the equation 50.27h = 4.19. Solve, and you find that h = 0.083.

17 B If the cube”s surface area is 6x, then x is the area of one face. Pick an easy number, and Plug In! Suppose x is 4. That means that the length of any edge of the cube is 2, and that the cube”s volume is 8. Just plug x = 4 into all of the answer choices, and find the one that gives you 8. (B) does the trick. (E) is the formula for the volume of a cube with edge x.

36 C Plug In! Suppose the sphere”s original radius is r = 2, which would give it a surface area of 50.3. If that radius is then increased by b = 1, the new radius is 3. The sphere would then have a surface area of 113.1. That”s an increase of 62.8. Plug r = 2 and b = 1 into the answer choices; the one that gives you 62.8 is correct. That”s (C).

40 B Just Plug In any values for b and h that obey the proportion b = 2h. Then plug those values into the formula for the volume of a pyramid.

Inscribed solids

32 B The long diagonal of the rectangular solid is the diameter of the sphere. Just find the length of the long diagonal and divide it in half.

35 C Calculate the volume of each shape separately. The cube”s volume is 8; the cylinder, with a radius of 1 and a height of 2, has a volume of 6.28. The difference between them is 1.72.

38 B The cube must have the dimensions 1 by 1 by 1. That means that the cone”s base has a radius of 0.5 and that the cone”s height is 1. Plug these numbers into the formula for the volume of a cone, and you should get 0.26.

Rotation solids

34 C This rotation will generate a cylinder with a radius of 2 and a height of 5. Its volume is 62.8.

39 D This rotation will generate a cone lying on its side, with a height of 5 and a radius of 3. Its volume is 47.12.

46 D Here”s an odd one. The best way to think about this one is as two triangles, base to base, being rotated. The rotation will generate two cones placed base to base, one right-side-up and one upside-down. Each cone has a radius of 3 and a height of 3. The volume of each cone is 28.27. The volume of the two together is 56.55.

Changing dimensions

13 E Just Plug In a value for the radius of sphere A, say 2. So the radius of sphere B is 6. Use the volume formula: A has volume π(2)² = π(8), and B has volume ≠(6)³ = ≠(216). If you make a ratio, the ≠ cancels, and you have = .

18 D Plug In for the dimensions of the rectangular solid so that the volume is 24. So pick l = 3, w = 4, and h = 2. The volume of the solid which the question asks for will then be 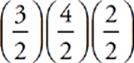= 3.

21 B Plug In for the length of the edge of the cube—try 2. So the surface area formula gives you 6(2)² = 24, and the volume of the cube is 8. Increasing this by a factor of 2.25 gives you a new surface area of 54. Setting the surface area formula equal to this gives you a length of 3 for the new, increased edge. So the new volume is 27. 27 ÷ 8 gives you 3.375 for the increase between the old and new volumes.

Chapter 7: Coordinate Geometry

The coordinate plane

1 Point E, quadrant II

2 Point A, quadrant I

3 Point C, quadrant IV

4 Point D, quadrant III

5 Point B, quadrant I

The equation of a line

7 A You can plug the line”s slope m and the given point (x, y) into the slope-intercept equation to get 1 = 0.6(3) + b. So b = −0.8. So the equation is y = 0.6x − 0.8. To find the point that is also on this line, go to each answer choice and plug the x-coordinate into the formula. You”ll have the right answer when the formula produces a y-coordinate that matches the given one.

10 E Once again, get the line into slope-intercept form, y = 5x − 4. Then Plug In zero. You get a y-value of −4. Notice that this is the y-intercept (the value of y when x = 0).

11 B Put the line into the slope-intercept formula by isolating y. So y = −3x + 4 and the slope is −3.

19 D You can figure out the line formula (y = mx + b) from the graph. The line has a y-intercept (b) of −2, and it rises 6 as it runs 2, giving it a slope (m) of 3. Use those values of m and b to test the statements in the answer choices.

Slope

4 C Use the slope formula on the point (0,0) and (−3, 2): .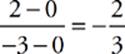

17 D Draw it. Remember that perpendicular lines have slopes that are negative reciprocals of each other. A line containing the origin and the point (2, −1) has a slope of −. The perpendicular line must then have a slope of 2. Quickly move through the answer choices, determining the slope of a line passing through the given point and the origin. The one that gives a slope of 2 is correct.

23 A Once again, the slope-intercept formula is your most powerful tool. Isolate y, and you get y = −3x + 5. The line must then have a slope of −3 and a y-intercept of 5. Only (A) and (D) show lines with negative slope, and the line in (D) has a slope which is between −1 and 0, because it forms an angle with the x-axis that is less than 45°.

47 D Remember that perpendicular lines have slopes that are negative reciprocals of each other. The slopes of x and y are therefore negative reciprocals—you can think of them as x and −. The difference between them will therefore be the sum of a number and its reciprocal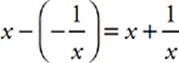: x − = x + . If x = 1, then the sum of x and its reciprocal is 2; if x = 5, then the sum of x and its reciprocal is 5.2; but no sum of a number and its reciprocal can be less than 2. A sum of 0.8 is impossible.

Line segments

12 D Use the distance formula on the points (−5, 9) and (0, 0).

19 E Drawing a rough sketch and approximating allows you to eliminate (A) and (B). Then, plug the points you know into the midpoint formula and PITA for the coordinates of B. The average of −4 and the x-coordinate of B is 1. The average of 3 and the y-coordinate of B is −1. That makes B the point (6, −5).

27 D You”ll essentially be using the distance formula on (2, 2) and the points in the answer choices. (−5, −3) is the point at the greatest distance from (2, 2).

General equations (parabolas)

34 C This is a quadratic function, which always produces a parabola. If a parabola has a maximum or minimum, then that extreme value is the parabola”s vertex. Just find the vertex. The x-coordinate is −, which is 3 in this case. The y-coordinate will be f(3), or −1.

37 B Use that vertex formula again. The x-coordinate is −, which is −1 in this case. That”s enough to get you the right answer. (If you needed the y-coordinate as well, you”d just Plug In x = −1 and solve for y.)

38 D At every point on the x-axis, y = 0. Plug each of the answer choices in for x, and see which one gives you y = 0. You could also put in 0 for y and solve for x; the solutions are 1 and 5.

General equations (circles)

30 B Just plug each point into the equation. The one that does not make the equation true is not on the circle.

34 E If S and T are the endpoints of a diameter, then the distance between them is 8. If they are very close to each other on the circle, then the distance between them approaches zero. The distance between S and T cannot be determined.

50 C Notice that because the y”s equal 0, you can cancel out the y”s in all the answer choices. Plug In the points: (2, 0) works in (C), (D), and (E), but (10, 0) works in (A), (B), and (C). It must be (C).

General equations (ellipses)

15 E Because a = 4 and b = 5, the minor axis is 2(4) = 8 and the major axis is 2(5) = 10.

40 C For an ellipse in its general form, the center is (h, k), which in this case is (−5, 3).

General equations (hyperbolas)

38 B Like circles and ellipses, hyperbolas in general form have their centers at (h, k). This one is centered at (−4, −5).

Triaxial coordinates

29 C This is once again a job for the Super Pythagorean theorem, which is simply another version of the 3-D distance formula. It”s just like finding the long diagonal of a box which is 5 by 6 by 7. Set up this equation: d ² = 5² + 6² + 7², and solve.

34 B A point will be outside the sphere if the distance between it and the origin is greater than 6. Use the Super Pythagorean theorem to measure the distance of each point from the origin.

Chapter 8: Trigonometry

Trig functions in right triangles

1 sin θ = = 0.6; cos θ = = 0.8; tan θ = = 0.75

2 sin θ = = 0.385; cos θ = = 0.923; tan θ = = 0.417

3 sin θ = = 0.96; cos θ = = 0.28; tan θ = = 3.429

4 sin θ = = 0.6; cos θ = = 0.8; tan θ = = 0.75

Completing triangles

1 AB = 3.38; CA = 7.25; ∠B = 65°

2 EF = 2.52; FD = 3.92; ∠D = 40°

3 HJ = 41.41; JK = 10.72; ∠J = 75°

4 LM = 5.74; MN = 8.19; ∠N = 35°

5 TR = 4.0; ∠S = 53.13°; ∠T = 36.87°

6 YW = 13; ∠W = 22.62°; ∠Y = 67.38°

Trigonometric identities

25 D Use FOIL on these binomials, and you get 1 − sin² x. Because sin² x + cos² x = 1, you know that 1 − sin² x = cos² x.

31 C Express tan x as . The cosine then cancels out on the top of the fraction, and you”re left with , or 1.

39 A The term (sin x)(tan x) can be expressed as (sin x) 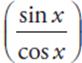or 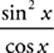. The first and second terms can then be combined: 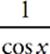− 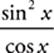= 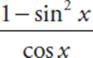. Because 1 − sin² x = cos² x, this expression simplifies to cos x.

42 E Break the fraction into two terms, as follows: 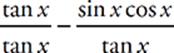. The first term simplifies to 1, and the second term becomes easier to work with when you express the tangent in terms of the sine and cosine: 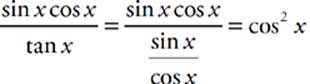. The whole expression then equals 1 − cos² x, or sin² x.

Other trig functions

19 E Express the function as a fraction: 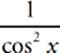− 1. You can then combine the terms by changing the form of the second term: 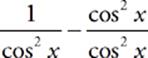. This allows you to combine the terms, like this: 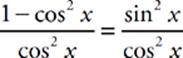= tan² x.

23 D Express the cotangent as a fraction, as follows: 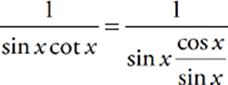. The sin x then cancels out, leaving you with 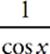, or sec x.

24 A Express the cotangent as a fraction, and the second term can be simplified: (cos x)(cot x) = cos x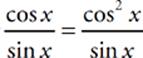. Express both terms as fractions, and the terms can be combined: 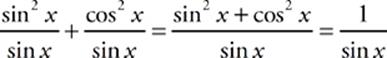or csc x.

Angle equivalencies

18 A Draw the unit circle. −225° and 135° are equivalent angle measures, because they are separated by 360°. Or just PITA, to see which value of x works in the equation.

21 D Draw the unit circle. 300° and 60° are not equivalent angles, but they have the same cosine. It”s a simple matter to check with your calculator. Or you could just PITA.

26 B PITA and use your calculator!

30 C PITA and use your calculator!

36 D Plug In a value for θ, from the ranges in the answer choices. If θ = 60°, then (sin 60°)(cos 60°) = 0.433, which is not less than zero. So cross off any answer choices that contain 60°—(A), (B), (C), and (E).

Degrees and radians

Non-right triangles

1 a = 8.26, ∠B = 103.4°, ∠C = 34.6° Your calculator will give you ∠B = 76.6°, but you need 180° − 76.6° = 103.4° in order to have an obtuse angle with the same distance from 90° as 76.6°.

2 ∠A = 21.79°, ∠B = 120.0°, ∠C = 38.21°

3 c = 9.44, ∠B = 57.98°, ∠C = 90.02°

Polar coordinates

39 C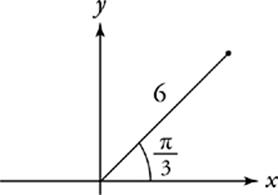

Draw it! The x-coordinate of the point is , or 3. The y-coordinate is , which is 5.196.

42 B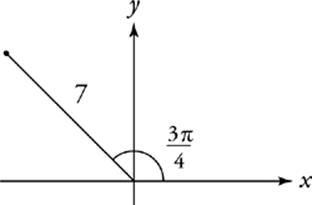

Draw it! The y-value of a point is its distance from the x-axis. The y-coordinate of this point is 7 sin , which equals 4.949.

45 B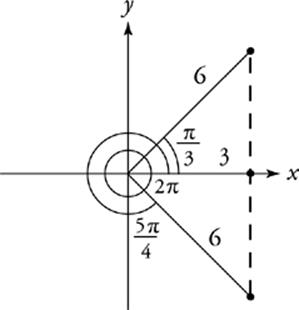

Draw it! In rectangular coordinates, A, B, and C have x-coordinates of 3. This means that they are placed in a straight vertical line. They define a straight line, but not a plane or space.

Chapter 9: Functions

$&#*@! functions

34 B Just follow instructions on this one, and you get −64 − (−27), or −64 + 27, which is −37. (C) is a Joe Bloggs answer.

35 A You”ve just got to plow through this one. The original expression ¥5 + ¥6 becomes 5(3)² + 5(4)², which equals 125. Work through the answer choices from the top to find the one that gives you 125. (E) is a Joe Bloggs answer.

36 B The function §a leaves even numbers alone and flips the signs of odd numbers. That means that the series §1 + §2 + §3…§100 + §101 will become (−1) + 2 + (−3) + 4 + (−5) … + 100 + (−101). Rather than adding up all those numbers, find the pattern: −1 and 2 add up to 1; −3 and 4 add up to 1; and so on, all the way up to −99 and 100. That means 50 pairs that add up to 1, plus the −101 left over. 50 + −101 = −51.

Functions without weird symbols

14 E f(−1) = (−1)² − (−1)³ = 1 − (−1) = 1 + 1 = 2

17 B f(7) = 10.247. f(8) = 11.314. That”s a difference of 1.067.

26 B g(3) = 3³ + 3² − 9(3) − 9 = 0

29 D f(3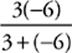, −6) = = = 6

30 A PITA for n, plug each answer choice into h(x), and see which one spits out 10. Alternately, you could solve 10 = n² + n − 2 by setting n equal to 0 and factoring; the solutions are −4 and 3.

33 E The greatest factor of 75 not equal to 75 is 25. Therefore, f(75) = 75 • 25 = 1,875.

34 E If y = 3, then g(−y) = g(−3). Because −3 < 0, g(−3)= 2|−3| = 2(3) = 6.

Compound functions

17 D Plug In a number for x. Try 3. f(g(3)) = f(7) = 21, and g(f(3)) = g(9) = 13, so the difference is 8.

24 E To evaluate f(g(−2)), first find the value of g(−2), which equals (−2)³ − 5, or −13. Then put that result into f(x): f(−13) = |−13|− 5 = 13 − 5 = 8.

25 B Let”s PITA. Plug In 3 for g(x): f(3) = 5 + 3(3) = 14. Nope—eliminate (A). Now let”s Plug In 4 for g(x): f(4) = 5 + 3(4) = 17. Any of the other choices would leave a variable in the compound function, so (B) is the answer.

32 D Just Plug In a nice little number, perhaps x = 3. You get g(f(3)) = g(64) = 12. Now just plug 3 into the answers for x, to see which one hits your target number, 12.

36 C f(g(3)) = 5. g(f(3)) = 3.196. The difference between them is 1.804.

Inverse functions

22 B Plug a number into f(x). For example, f(2) = 1.5. Since g(1.5) = 2, the correct answer is the function that turns 1.5 back into 2. (B) does the trick.

33 B PITA, starting with (C). Take each answer choice, plug it in for x in f(x), and see which one spits out 9.

35 E The fact that f(3) = 9 doesn”t tell you what f(x) is. It”s possible that f(x) = x², or that f(x) = 3x, or that f(x) = 2x + 3, and so on. Each of these functions would have a different inverse function. The definition of the inverse function cannot be determined.

Domain and range

24 A This function factors to f(x) = 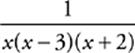. Three values of x will make this fraction undefined: −2, 0, and 3. The function”s domain must exclude these values.

27 E This function factors to g(x) = . The product of these binomials must be nonnegative (that means positive or zero), since a square root of a negative number is not a real number. The product will be nonnegative when both binomials are negative (x ≤ −2) or when both are nonnegative (x ≥ 6). The function”s domain is {x: x ≤ −2 or x ≥ 6}.

30 D Take this one step at a time. Because a number raised to an even power can”t be negative, the range of a² is the set of nonnegative numbers—that is, {y: y ≥ 0}. The range of a² + 5 is found by simply adding 5 to the range of a², {y: y ≥ 5}. Finally, to find the range of 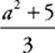, divide the range of a² + 5 by 3, 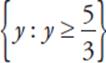, or {y: y ≥ 1.67}. The correct answer is (D).

34 D Because this is a linear function (without exponents), you can find its range over the given interval by Plugging In the bounds of the domain. f(−1) = −1, and f(4) = 19. Therefore the range of f is {y: −1 ≤ y ≤ 19}.

Identifying graphs of functions

9 D It”s possible to intersect the graph shown in (D) twice with a vertical line, where the point duplicates an x-value on the curve.

15 B It”s possible to intersect the graph shown in (B) more than once with a vertical line, at each point where the graph becomes vertical.

Range and domain in graphs

17 A The graph has a vertical asymptote at x = 0, so 0 must be excluded from the domain of f.

24 D Only two x-values are absent from the graph, x = 2 and x = −2. The domain must exclude these values. This can be written as {x: x ≠ −2, 2} or {x: |x| ≠ 2}.

28 C The graph extends upward forever, but never goes lower than −3. Its range is therefore {y: y ≥ −3}.

37 C Plug In a big number, such as x = 1,000. It looks like y approaches 5.

48 E Plug the numbers you are given into the equation to see what happens to the graph. In I, if x = 2, then y = −, which does not exist. Therefore I is definitely an asymptote, and you should eliminate answer choices without I in them, that is, (B) and (C). Now, try Plugging In a big number for x, like x = 1,000. y heads toward −1, which means y = −1 is also an asymptote, and III is correct. Cross off answer choices without III in them, in other words, (A) and (D). The correct answer is (E).

Roots of functions

16 D PITA! Plug In each choice for x into f(x) to see which one spits out 0.

19 C The function g(x) can be factored as g(x) = x(x + 3)(x − 2). Set this function equal to zero and solve for x. You”ll find the function has three distinct roots, −3, 0, and 2.

25 D The roots of a function are the x-values at which f(x) = 0. In short, the roots are the x-intercepts—in this case, −4, −1, and 2.

Symmetry in functions

6 D “Symmetrical with respect to the x-axis” means reflected as though the x-axis were a mirror. That is, the values of the function above the x-axis should match corresponding values below the x-axis.

17 E An even function is one for which f(x) = f(−x). This is true by definition of an absolute value. Confirm by Plugging In numbers.

Degrees of functions

31 E The graph shown has five visible distinct x-intercepts (zeros), so it must be at least fifth-degree. The degree of a function is determined by its greatest exponent. Only the function in answer choice (E) is at least a fifth-degree function.

35 D Since the degree of a function is determined by its greatest exponent, all you need to do in order to find the fourth-degree function is figure out the greatest exponent in each answer choice when it”s multiplied out. Remember, you don”t need to do all of the algebra; just see what the greatest exponent will be. Answer choice (A) is a second-degree function, because its highest-order term is x². Answer choices (B) and (C) are third-degree functions, because the highest-order term in each function is x³. Answer choice (E) is a fifth-degree function, since x • x • x³=x⁵. Only answer choice (D) is a fourth-degree function.

Chapter 10: Statistics and Sets

Statistics

25 B If the sum of a list”s elements is zero, then the mean must also be zero. It”s impossible to know what the median is; the list could be {0, 0, 0, 0, 0, 0, 0, 0, 0, 0} or {−9, 1, 1, 1, 1, 1, 1, 1, 1, 1}. Both lists add up to zero, but have different medians. The mode is not necessarily zero for the same reasons.

42 C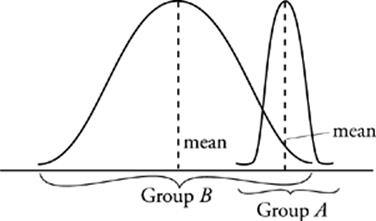

You can either draw a nice pair of bell curves like the ones we”ve made, or just Plug In some numbers. Imagine that Group A has the scores 5, 5, 5 and Group B has the scores 1, 5, 6. The mean of A is greater, and the standard deviation of B is greater (simply because the values are more spread out), but (A), (B), (D), and (E) are all false. (C) may sound vague, but go complain to ETS. Really, the stuff about the mean is just a smokescreen.

Probability

13 A There are only two things that can happen, rain or not rain. If 5 out of 12 possible outcomes mean rain, then the other 7 of the 12 possible outcomes must mean no rain.

16 A The probability that two events will occur together is the product of the chances that each will happen individually. The probability that these two events will happen together is • or .

20 B Out of a total of 741 cookies, 114 are burned. The probability of getting a burned cookie is therefore . That reduces to , which is equivalent to .

24 B For the product of the numbers to be odd, both numbers must be odd themselves. There”s a chance of getting an odd number on each die. The odds of getting odd numbers on both dice are • = = .

44 C This one”s pretty tricky. It”s difficult to compute the odds of getting “at least one basket” in three tries, since there are so many different ways to do it (basket-basket-basket, miss-miss-basket, basket-basket-miss, and so on). It”s a simpler solution to calculate the odds of Heather”s missing all three times. If the probability of her making a basket on any given try is , then the probability of her missing is . The probability of her missing three times in a row is • •, or . That means that Heather makes no baskets in 1 out of 125 possible outcomes. The other 124 possible outcomes must involve her making at least 1 basket.

Permutations, combinations, and factorials

27 B All committee questions are combination questions, because different arrangements of the same people don”t count as different committees. The number of permutations of 12 items in 4 spaces is 12 × 11 × 10 × 9, or 11,880. To find the number of combinations, divide this number by 4 × 3 × 2 × 1, or 24. You get 495.

31 E Even if you know how to simplify this algebraically, there are a few different ways to express the right answer. You may have to waste time getting your (technically correct) answer to look like ETS”s credited response. Plugging In numbers will always make your life easier. Let”s Plug In x = 3. 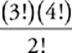= = 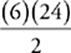72. (A) gives us 720, (B) gives us 40,320, (C) gives us 3, (D) gives us 12, and (E) gives us 72. It”s (E).

32 D The number of permutations of 6 items in 6 spaces is 6 × 5 × 4 × 3 × 2 × 1, or 720.

45 A Compute the number of combinations of females and males separately. The number of combinations of 17 females in 4 spaces is 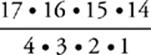, or 2,380. The number of combinations of 12 males in 3 spaces is 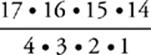, or 220. The total number of combinations is the product of these two numbers, 220 × 2,380, or 523,600.

Group questions

25 A Remember the group problem formula: Total = Group 1 + Group 2 + Neither − Both. Then Plug In the numbers from the question, so 530 = 253 + 112 + N − 23, and N = 188.

28 C Remember the group-problem formula: Total = Group 1 + Group 2 + Neither − Both. Then Plug In the numbers from the question, so T = 14 + 12 + 37 − 9 = 54.

42 B Plug In a number of tourists that you can easily take , , and of—like 30. If the total number of tourists is 30, then 10 speak Spanish, 12 speak French, and 15 speak neither language. Once again, plug these numbers into the group formula to get 30 = 10 + 12 + 15 − B. This simplifies to 30 = 37 − B, so B = 7. Seven tourists speak both Spanish and French. That”s of the whole group.

Chapter 11: Miscellaneous

Logarithms

1 2⁵ = 32, so log₂ 32 = 5

2 3⁴ = 81, so x = 81

3 10³ = 1,000, so log 1,000 = 3

4 4³ = 64, so b = 4

5 Exponents and logs undo each other, so = y

6 7⁰ = 1, so log₇ 1 = 0

7 The sidebar tells us that log_x x = 1

8 x to what power is x¹²? The 12^th power, of course! log_x x¹² = 12

9 1.5682—use your calculator

10 0.6990—use your calculator

Logarithmic rules

1 log 20

2 log₅ 2

3 log 3

4 log₄ 16 = 2

5 log 75

Logarithms in exponential equations

1 Take the log of both sides and use the power rule. Your new equation will be 4 log 2 = x log 3. Now divide both sides by log 3 and you get 4 = x. Using your calculator, you get x = 2.5237.

2 Use the Change of Base formula:
log₅ 18 = 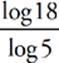= 1.7959

3 Use the definition of a logarithm to convert the equation: n = log 137 = 2.1367

4 Use the Change of Base formula:
log₁₂ 6 = 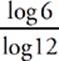= 0.7211

5 4^{x + 2} = = 80. Here”s a great place to use the rule of multiplying exponents with like bases.

6 Use the Change of Base formula:
log₂ 50 = 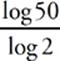= 5.6439

7 3^{x + 1} = (3^x)(x¹) = 21

8 Use the change of base formula for the left side of the equation. 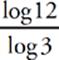= 2.2619. So you know that log₄ x = 2.2619. Now use the definition of logs to see that 42.2619 = x, and x is about 23. Make sure not to round too early so that your answer is as close to ETS”s answer as possible.

Natural logarithms

18 B The equation e^z = 8 converts into a natural logarithm: ln 8 = z. To find the value of z, just type ln 8 into your calculator and see what happens. You”ll get 2.07944.

23 C All you need to know to solve this one is that π ≈ 3.14 and e ≈ 2.718. Then it”s easy to put the quantities in order; just remember that you”re supposed to put them in descending order.

38 A To solve this equation, start by isolating the e term:
6 = 5
=
Then, use the definition of a logarithm to change the form of the equation:
In =
n = 3 In
Finally, use your calculator to evaluate the logarithm:
n = 3(−0.1823)
n = −0.5469

Visual perception

27 A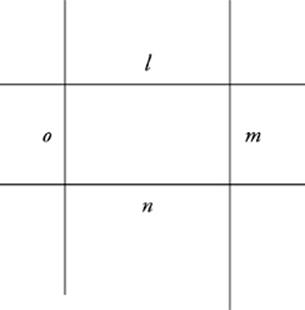

Drawing the described set of lines results in something looking like the above. As you can see, line l is parallel to line n, but neither of the other two statements is true.

42 D Whenever a circle intersects with a face of cube and pokes through (as opposed to touching at just one point), it creates a circle.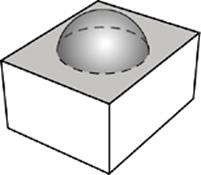

It”s probably easiest to get six intersections by having the sphere intersect with all six faces of the cube.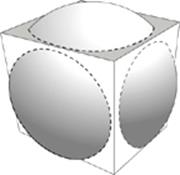

It”s also possible to get five by having nearly the same picture but moving the sphere up a little so as not to intersect with the base of the cube. Seven is too complicated, though; there are only six faces of the cube, so how are there going to be seven circles?

Arithmetic and geometric sequences

14 E An arithmetic sequence is formed by adding a value again and again to an original term. From the second term to a sixth term is 4 steps. Going from 4 to 32 is a change of 28 in four steps, making each step an increase of 7. The fifth term must then be 7 less than the sixth term, or 25.

19 E Going from the first to the seventh term of a sequence is 6 steps, and going from 2 to 16 is a difference of 14. That makes each step an increase of , or 2.33. To find the 33rd term, plug these numbers into the formula for the nth term of an arithmetic sequence: a₃₃ = 2 + (33 − 1) = 2 + 74 = 76.67.

26 D From the second term of a sequence to the fourth is two steps—that is, 4 is multiplied by the factor r twice to get to 25. That means that 4 × r² = 25. Solve for r and you”ll find that r = 2.5. Just punch 4 into your calculator as the second term, and keep multiplying by 2.5 until you”ve counted up to the ninth term. Or figure out that the first term in the sequence is , or 1.6. Then just plug those values into the formula for the nth term of a geometric sequence: a₉ = 1.6 × 2.5⁸ = 2441.41.

34 C Because no end term is given, this is an infinite geometric sequence. It”s decreasing, not increasing, so its sum is finite. Its first term is 3, and each successive term is multiplied by a factor of . Plug those values into the formula for the sum of an infinite geometric sequence, sum = 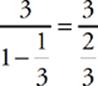= 4.5 Of course, you can also approximate. If you add the first four terms on your calculator, you get 4.4444. So you can eliminate (A) and (B). All the numbers you add after this are really tiny, so you”ll never reach 5.0 or an infinite size. Therefore you can eliminate (D) and (E).

Limits

30 B This expression factors into 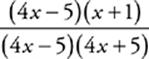. The binomial 4x − 5 cancels out, leaving you with 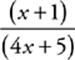This expression is no longer undefined when x equals 1.25, so just plug 1.25 into the expression—the result is the limit. Alternatively, plug something very close to 1.25 (say, 1.24999) into the expression and use your calculator to evaluate it. It should be very close to B.

38 A This expression factors into 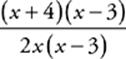. The binomial x − 3 cancels out, leaving you with . This expression is no longer undefined when x = 3, so just plug x = 3 into the expression to obtain the limit. Alternatively, plug in a number very close to 3 (say, 2.99) into the expression and use your calculator to evaluate it. The result should be very close to A.

40 E This expression factors into 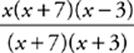. The binomial x + 7 factors out, leaving you with 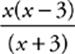Notice, however, that the expression is still undefined when x = −3. The limit remains undefined and does not exist. Alternatively, plug in a number very close to −3 (say, −2.99) and evaluate the expression. Notice that it doesn”t appear to be close to any of the numbers in the answer choices. If you want to verify that it”s not going anywhere, try numbers even closer to −3 (say, −2.999 or −2.9999) until you”re convinced that the limit does not exist.

Vectors

36 D You can see from the graph that the components of are (−2, 4), and the components of are (−2, −1). So the components of must be the result of adding the components, (−4, 3). If you draw this, you can see that the magnitude of is the length of the hypotenuse of a 3:4:5 triangle.

41 B Subtracting the components of a and b, you get (5, 12). So the magnitude of c is the length of the hypotenuse of a 5:12:13 triangle.

44 E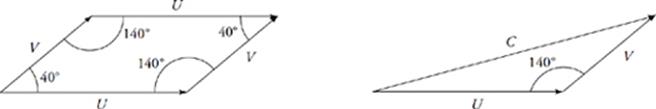
Either move u so that its tip points to the tail of v or vice-versa; you”ll get the same result either way. In any event, the angle between the vectors is now 140°. Draw in the resulting vector (we”ll label it with a length of c) from tail to head, closing off the triangle. The Law of Cosines then gives us c² = 9² + 7²− 2(9)(7) cos 140°. So c = 15.05. You could also approximate c, once you draw in the resulting vector.

Logic

28 D The basic statement here is: sophomore → not failing. The contrapositive of this statement would be: failing → not sophomore. Answer choice (D) is the contrapositive.

33 B The basic statement here is: arson → building burns. The contrapositive would be: no building burns → no arson. Answer choice (B) directly contradicts the contrapositive.

35 C The basic statement here is: not genuine → ruby. The contrapositive would be: not ruby → genuine. Answer choice (C) paraphrases the contrapositive.

Imaginary numbers

25 C Remember that the powers of i repeat in a cycle of four. Divide 51 by 4, and you”ll find that the remainder is 3. i ⁵¹ will be equal to i ³, which is −i.

36 D Only (D) contains two values that do not cancel each other out. i ¹¹ = i ³(i ⁸) = i ³(1) = i ³ = −i, and i ⁹ = i(i ⁸) = i(1) = i. So −i − i = −2i, not 0.

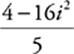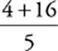40 B Use FOIL on the top of the fraction, and you get , or = = 4

43 D Plot the point on the complex plane; it will have a real coordinate of 5 and an imaginary coordinate of −12. The Pythagorean theorem will give you the point”s distance from the origin, 13.

Polynomial division

21 C Divide both sides by (x + 2). Now Plug In x = 2. g(2) = = 4, your target number. Plug In 2 for x in the answer choices, to see which one turns into 4. Only (C) works.

27 A Plug In x = 10, and use your calculator. When 970 is divided by 7, you get 138.571. Well, 7 × 138 = 966, so the remainder is 4, your target number. (B) is wrong. (C), (D), and (E) are nowhere near 4, so only (A) can be correct. (E) is the answer without the remainder.

What is the matrix?

30 D In matrix multiplication, the two inner dimensions (the number of columns in the first matrix and the number of rows in the second matrix) must be equal; the resulting matrix will have as many rows as the first matrix and as many columns as the second matrix.

40 E The determinant is (1)(0) − (2)(−1) = 2.

45 C You can write the matrix next to itself; then the six parts of the formula form straight (diagonal) lines. So we get 0 + (−4) + (−3) − (−2) − 0 − (−6) = 1. Alternatively, if you have a calculator that can do matrices, use your calculator.

46 A Make a matrix out of the coefficients on the left-hand side of the equations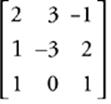



The determinant is −6 + 6 + 0 − 3 − 0 − 3 = −6.
Alternatively, if you have a calculator that can do matrices, use your calculator.