Solid Geometry - SAT Math 1 & 2 Subject Tests

SAT Math 1 & 2 Subject Tests

Chapter 6 Solid Geometry

Questions about solid geometry frequently test plane geometry techniques. They”re difficult mostly because the added third dimension makes them harder to visualize. You”re likely to run into three or four solid geometry questions on either one of the Math Subject Tests, however, so it”s important to practice. If you”re not the artistic type and have trouble drawing cubes, cylinders, and so on, it”s worthwhile to practice sketching the shapes in the following pages. The ability to make your own drawing is often helpful.

PRISMS

Prisms are three-dimensional figures that have two parallel bases that are polygons. Cubes and rectangular solids are examples of prisms that ETS often asks about. In general, the volume of a prism is given by the following formula:

Volume of a Prism

V = Bh

In this formula, B represents the area of either base of the prism (the top or the bottom), and h represents the height of the prism (perpendicular to the base). The formulas for the volume of a rectangular solid, a cube, and a cylinder all come from this basic formula.

Area and Volume

In general the volume of a
shape involves the area of
the base, often referred to
as B, and the height, or h,
of the solid.

RECTANGULAR SOLID

A rectangular solid is simply a box; ETS also sometimes calls it a rectangular prism. It has three distinct dimensions: length, width, and height. The volume of a rectangular solid (the amount of space it contains) is given by this formula:

Volume of a Rectangular Solid

V = lwh

The surface area (SA) of a rectangular solid is the sum of the areas of all of its faces. A rectangular solid”s surface area is given by the formula on the next page.

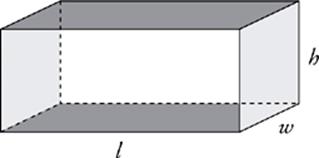
Surface Area of a Rectangular Solid

SA = 2lw + 2wh + 2lh

The volume and surface area of a solid make up the most basic information you can have about that solid (volume is tested more often than surface area). You may also be asked about lengths within a rectangular solid—edges and diagonals. The dimensions of the solid give the lengths of its edges, and the diagonal of any face of a rectangular solid can be found using the Pythagorean theorem. There”s one more length you may be asked about—the long diagonal (or space diagonal) that passes from corner to corner through the center of the box. The length of the long diagonal is given by this formula:

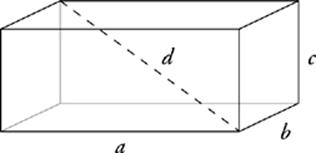
Long Diagonal of a Rectangular Solid (Super Pythagorean Theorem)

a² + b² + c² = d²

This is the Pythagorean theorem with a third dimension added, and it works just the same way. This formula will work in any rectangular box. The long diagonal is the longest straight line that can be drawn inside any rectangular solid.

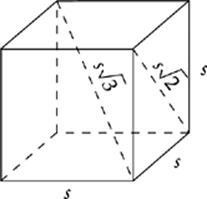
CUBES

A cube is a rectangular solid that has the same length in all three dimensions. All six of its faces are squares. This simplifies the formulas for volume, surface area, and the long diagonal.

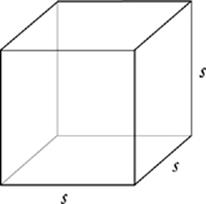
Volume of a Cube

V = s³

Surface Area of a Cube

SA = 6s²

Face Diagonal of a Cube

f = s

Long Diagonal of a Cube

d = s

CYLINDERS

A cylinder is like a prism but with a circular base. It has two important dimensions—radius and height. Remember that volume is the area of the base times the height. In this case, the base is a circle. The area of a circle is πr². So the volume of a cylinder is πr²h.

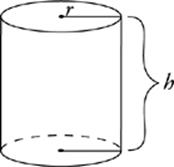
Volume of a Cylinder

V = πr²h

The surface area of a cylinder is found by adding the areas of the two circular bases to the area of the rectangle you”d get if you unrolled the side of the cylinder. That boils down to the following formula:

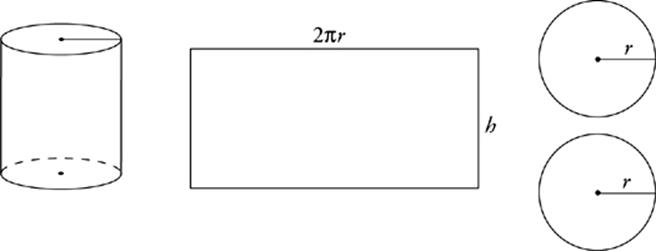
Surface Area of a Cylinder

SA = 2πr² + 2πrh

The longest line that can be drawn inside a cylinder is the diagonal of the rectangle formed by the diameter and the height of the cylinder. You can find its length with the Pythagorean theorem.

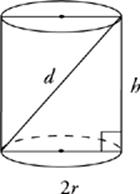
d² = (2r)² + h ²

CONES

If you take a cylinder and shrink one of its circular bases down to a point, then you have a cone. A cone has three significant dimensions which form a right triangle—its radius, its height, and its slant height, which is the straight-line distance from the tip of the cone to a point on the edge of its base. The formulas for the volume and surface area of a cone are given in the information box at the beginning of both of the Math Subject Tests. The formula for the volume of a cone is pretty straightforward:

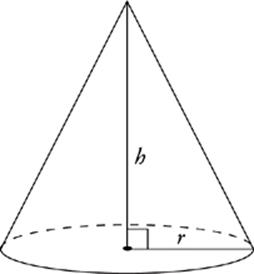
Volume of a Cone

V = πr²h

Connect the Dots

Notice that the volume of
a cone is just one-third of
the volume of a circular
cylinder. Make memorizing
easy!

But you have to be careful computing surface area for a cone using the formula provided by ETS. The formula at the beginning of the Math Subject Tests is for the lateral area of a cone—the area of the sloping sides—not the complete surface area. It doesn”t include the circular base. Here”s a more useful equation for the surface area of a cone.

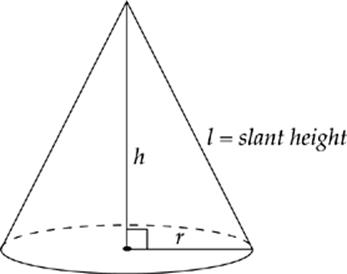
Surface Area of a Cone

SA = πrl + πr²

If you want to calculate only the lateral area of a cone, just use the first half of the above formula—leave the πr² off.

SPHERES

A sphere is simply a hollow ball. It can be defined as all of the points in space at a fixed distance from a central point. The one important measure in a sphere is its radius. The formulas for the volume and surface area of a sphere are given to you at the very beginning of both Math Subject Tests. That means that you don”t need to have them memorized, but here they are anyway:

Volume of a Sphere

V = πr³

Surface Area of a Sphere

SA = 4πr²

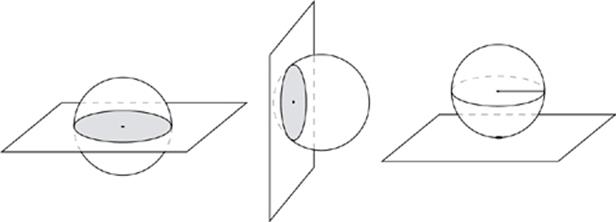
The intersection of a plane and a sphere always forms a circle unless the plane is tangent to the sphere, in which case the plane and sphere touch at only one point.

PYRAMIDS

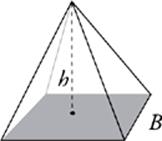
A pyramid is a little like a cone, except that its base is a polygon instead of a circle. Pyramids don”t show up often on the Math Subject Tests. When you do run into a pyramid, it will almost always have a rectangular base. Pyramids can be pretty complicated solids, but for the purposes of the Math Subject Tests, a pyramid has just two important measures—the area of its base and its height. The height of a pyramid is the length of a line drawn straight down from the pyramid”s tip to its base. The height is perpendicular to the base. The volume of a pyramid is given by this formula.

Connect the Dots

Notice that the volume of
a pyramid is just one-third
of the volume of a prism.
Make memorizing easy!

Volume of a Pyramid

V = Bh

(B = area of base)

It”s not really possible to give a general formula for the surface area of a pyramid because there are so many different kinds. At any rate, the information is not generally tested on the Math Subject Tests. If you should be called upon to figure out the surface area of a pyramid, just figure out the area of each face using polygon rules, and add them up.

TRICKS OF THE TRADE

Here are some of the most common solid geometry question types you”re likely to encounter on the Math Subject Tests. They occur much more often on the Math Level 2 Subject Test than on the Math Level 1 Subject Test, but they can appear on either test.

Triangles in Rectangular Solids

Many questions about rectangular solids are actually testing triangle rules. Such questions generally ask for the lengths of the diagonals of a box”s faces, the long diagonal of a box, or other lengths. These questions are usually solved using the Pythagorean theorem and the Super Pythagorean theorem that finds a box”s long diagonal (see the section on Rectangular Solids).

DRILL

Here are some practice questions using triangle rules in rectangular solids. The answers to these drills can be found in Chapter 12.

32. What is the length of the longest line that can be drawn in a cube of volume 27 ?

(A) 3.0

(B) 4.2

(D) 5.2

(E) 9.0

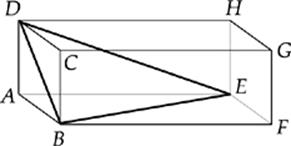
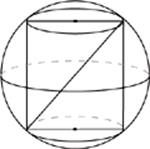
36. In the rectangular solid shown, if AB = 4, BC = 3, and BF = 12, what is the perimeter of triangle EDB ?

(A) 27.33

(B) 28.40

(D) 29.50

(E) 30.37

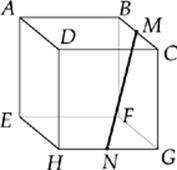
39. In the cube above, M is the midpoint of BC, and N is the midpoint of GH. If the cube has a volume of 1, what is the length of MN ?

(A) 1.23

(B) 1.36

(D) 1.73

(E) 1.89

Volume Questions

Many solid geometry questions test your understanding of the relationship between a solid”s volume and its other dimensions—sometimes including the solid”s surface area. To solve these questions, just plug the numbers you”re given into the solid”s volume formula.

Drill

Try the following practice questions. The answers to these drills can be found in Chapter 12.

17. The volume and surface area of a cube are equal. What is the length of an edge of this cube?

(A) 1

(B) 2

(D) 6

(E) 9

24. A rectangular solid has a volume of 30, and its edges have integer lengths. What is the greatest possible surface area of this solid?

(A) 62

(B) 82

(D) 94

(E) 122

28. The water in Allegra”s swimming pool has a depth of 7 feet. If the area of the pentagonal base of the pool is 150 square feet, then what is the volume, in cubic feet, of the water in her pool?

(A) 57

(B) 50

(D) 5,250

(E) It cannot be determined from the information given.

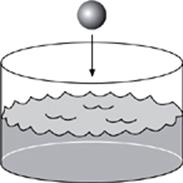
43. A sphere of radius 1 is totally submerged in a cylindrical tank of radius 4, as shown. The water level in the tank rises a distance of h. What is the value of h ?

(A) 0.072

(B) 0.083

(D) 0.108

(E) 0.123

17. A cube has a surface area of 6x. What is the volume of the cube?

(A)

(B)

(D) 36x²

(E) x³

36. A sphere has a radius of r. If this radius is increased by b, then the surface area of the sphere is increased by what amount?

(A) b²

(B) 4πb²

(D) 8πrb + 2rb + b²

(E) 4πr²b²

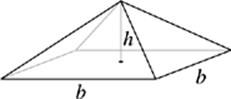
40. If the pyramid shown has a square base with edges of length b, and b = 2h, then which of the following is the volume of the pyramid?

(A)

(B)

(D) 8h² − h

(E)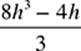

Inscribed Solids

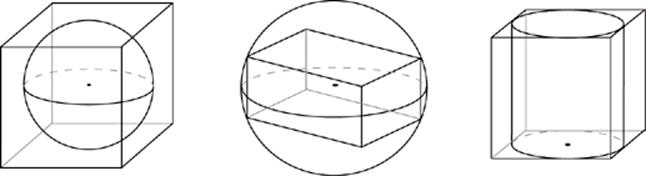
Some questions on the Math Subject Tests will be based on spheres inscribed in cubes or cubes inscribed in spheres (these are the most popular inscribed shapes). Occasionally you may also see a rectangular solid inscribed in a sphere, or a cylinder inscribed in a rectangular box, etc. The trick to these questions is always figuring out how to get from the dimensions of one of the solids to the dimensions of the other.

Following are a few basic tips that can speed up your work on inscribed solids questions.

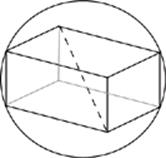
· When a cube or rectangular solid is inscribed in a sphere, the long diagonal of that solid is equal to the diameter of the sphere.

· When a cylinder is inscribed in a sphere, the sphere”s diameter is equal to the diagonal of the rectangle formed by the cylinder”s heights and diameter.

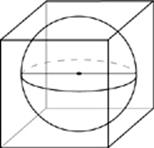
· When a sphere is inscribed in a cube, the diameter of the sphere is equal to the length of the cube”s edge.

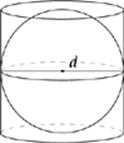
· If a sphere is inscribed in a cylinder, both solids have the same diameter.

Most inscribed solids questions fall into one of the preceding categories. If you run into a situation not covered by these tips, just look for the way to get from the dimensions of the inner shape to those of the external shape, or vice versa.

DRILL

Here are some practice inscribed solids questions. The answers to these drills can be found in Chapter 12.

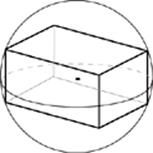
32. A rectangular solid is inscribed in a sphere as shown. If the dimensions of the solid are 3, 4, and 6, then what is the radius of the sphere?

(A) 2.49

(B) 3.91

(D) 5.62

(E) 7.81

35. A cylinder is inscribed in a cube with an edge of length 2. What volume of space is enclosed by the cube but not by the cylinder?

(A) 1.41

(B) 1.56

(D) 3.81

(E) 4.86

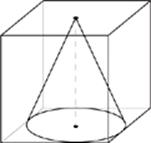
38. A cone is inscribed in a cube of volume 1 in such a way that its base is inscribed in one face of the cube. What is the volume of the cone?

(A) 0.21

(B) 0.26

(D) 0.42

(E) 0.67

Solids Produced by Rotation

Three types of solids can be produced by the rotation of simple two-dimensional shapes—spheres, cylinders, and cones. Questions about solids produced by rotation are generally fairly simple; they usually test your ability to visualize the solid generated by the rotation of a flat shape. Sometimes, rotated solids questions begin with a shape in the coordinate plane—that is, rotated around one of the axes or some other line. Practice will help you figure out the dimensions of the solid from the dimensions of the original flat shape.

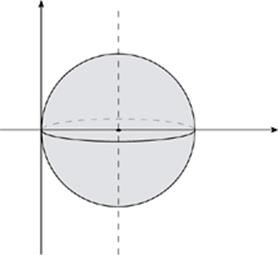
A sphere is produced when a circle is rotated around its diameter. This is an easy situation to work with, as the sphere and the original circle will have the same radius. Find the radius of the circle, and you can figure out anything you want to about the sphere.

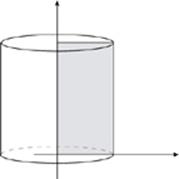
A cylinder is formed by the rotation of a rectangle around a central line or one edge.

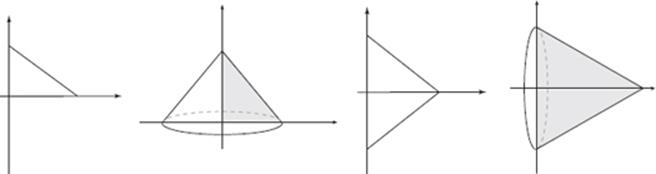
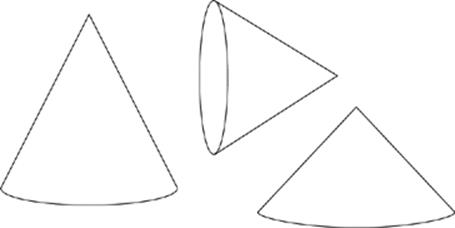
A cone is formed by rotating a right triangle around one of its legs (think of it as spinning the triangle) or by rotating an isosceles triangle around its axis of symmetry. Another way of thinking about it is if you spun the triangle in the first figure above around the y-axis (so you”re rotating around the leg that”s sitting on the y-axis) you would get the second figure. Likewise, if you spun the third figure above around the x-axis (so you”re rotating around the axis of symmetry), you would end up with the fourth figure.

DRILL

Try these rotated solids questions for practice. The answers to these drills can be found in Chapter 12.

34. What is the volume of the solid generated by rotating rectangle ABCD around AD ?

(A) 15.7

(B) 31.4

(D) 72.0

(E) 80.0

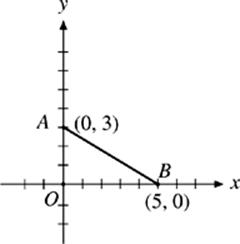
39. If the triangle created by OAB is rotated around the x-axis, what is the volume of the generated solid?

(A) 15.70

(B) 33.33

(D) 47.12

(E) 78.54

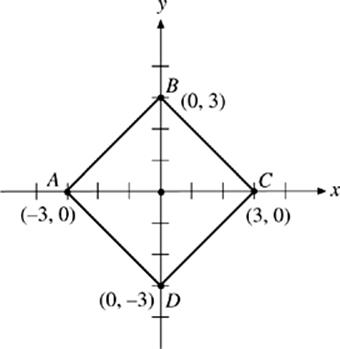
46. What is the volume generated by rotating square ABCD around the y-axis?

(A) 24.84

(B) 28.27

(D) 56.55

(E) 84.82

Changing Dimensions

Some solid geometry questions will ask you to figure out what happens to the volume of a solid if all of its lengths are increased by a certain factor or if its area doubles, and so on. To answer questions of this type, just remember a basic rule.

When the lengths of a solid are increased by a certain factor, the surface area of the solid increases by the square of that factor, and the volume increases by the cube of that factor. This rule is true only when the solid”s shape doesn”t change—its length must increase in every dimension, not just one. For that reason, cubes and spheres are most often used for this type of question because their shapes are constant.

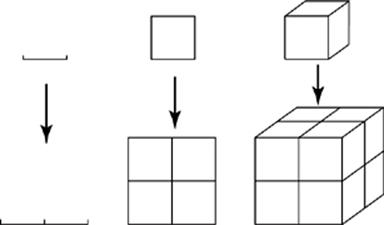
In the illustration above, a length is doubled, which means that the corresponding area is 4 times as great, and the volume is 8 times as great. If the length had been tripled, the area would have increased by a factor of 9, and the volume by a factor of 27.

DRILL

Try these practice questions. The answers to these drills can be found in Chapter 12.

13. If the radius of sphere A is one-third as long as the radius of sphere B, then the volume of sphere A is what fraction of the volume of sphere B ?

(A)

(B)

(C)

(D)

(E)

18. A rectangular solid with length l, width w, and height h has a volume of 24. What is the volume of a rectangular solid with length , width , and height ?

(A) 18

(B) 12

(D) 3

(E) 2

21. If the surface area of a cube is increased by a factor of 2.25, then its volume is increased by what factor?

(A) 1.72

(B) 3.38

(D) 5.06

(E) 5.64

Summary

· Solid geometry questions are often plane geometry questions in disguise.

· For the purposes of the SAT Math 1 & 2 Subject Tests, prisms are 3-dimensional figures with two parallel, identical bases. The bases can be any shape from plane geometry.

· The volume of a prism is the area of the base, often referred to as B, times the height, h.

· Let”s talk rectangular prisms:

· The formula for the volume of a rectangular prism is V = lwh.

· The formula for the surface area of a rectangular solid is SA = 2lw + 2wh + 2lh. Think about painting the outside of the figure. Find the area of each side.

· The Super Pythagorean theorem, which is helpful in solving questions about the diagonal of a rectangular prism, is a² + b² + c² = d².

· Let”s talk cubes. Remember that a cube is just a rectangular prism whose length, width, and height are equal. If you forget a formula, just use the rectangular prism formula!

· The volume of a cube is V = s³.

· The surface area of a rectangular solid is SA = 6s².

· Let”s talk cylinders. A cylinder is a prism whose bases are circles.

· The volume of a cylinder is V = πr²h.

· The surface area of a rectangular solid is SA = 2πr² + 2πrh. If you forget this, remember that you”re just painting the outside. So you”ll need the area of two circles and the area of the other piece, which, when rolled out (like a roll of paper towels), is a rectangle whose sides are the circumference of the circle and the height.

· A cone is similar to a cylinder except that one of its bases is merely a point.

· The formula for the volume of a cone is V = ≠ r² h, where the height must be perpendicular to the base.

· The formula for the surface area of a cone is SA = πrl + πr², where l is the slant height.

· A sphere is a hollow ball.

· The formula for the volume of a sphere is V = ≠ r³.

· The formula for the surface area of a cone is SA = 4πr².

· Pyramids are like cones, but the base is a plane geometry shape. The formula for the volume of a pyramid is V = Bh.

· Inscribed figures always have a line or curve that connects the inner figure to the outer figure.

· Questions about solids produced by rotation usually test your ability to visualize the solid created by the rotation of a flat shape.