University Mathematics Handbook (2015)
III. Analytic Geometry and Vectors
Chapter 8. Canonical Forms of Second-Order Surfaces in Space
8.1 Sphere
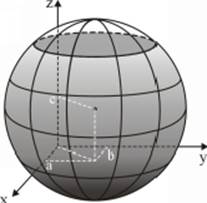
A sphere is the locus of all points in space for which the distance to point ![]() , or center is constant, and called radius.
, or center is constant, and called radius.
From the formula of distance of any point ![]() on the surface of the sphere, to point
on the surface of the sphere, to point ![]() , the sphere equation is obtained:
, the sphere equation is obtained:
![]()
The intersection lines of a sphere with any plane are circles.
Example: The line of intersection of plane ![]() , which is parallel to plane
, which is parallel to plane ![]() is the following circle
is the following circle
![]()
when ![]() .
.
8.2 Ellipsoid
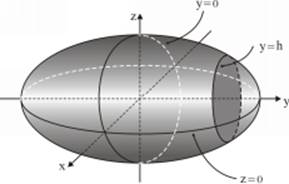
![]()
is an ellipsoid that is symmetric across planes ![]() ,
, ![]() ,
, ![]() .
.
Intervals ![]() on
on ![]() -axis,
-axis, ![]() on
on ![]() -axis and
-axis and ![]() on
on ![]() axis are called ellipsoid axis. The lines of intersection of ellipsoid with planes parallel to coordinate planes are ellipses.
axis are called ellipsoid axis. The lines of intersection of ellipsoid with planes parallel to coordinate planes are ellipses.
Example: ![]() , when
, when ![]() , is
, is
![]() .
.
Similarly, the lines of intersection with planes ![]() and
and ![]() are ellipses.
are ellipses.
8.3 One-Sheet Hyperboloid
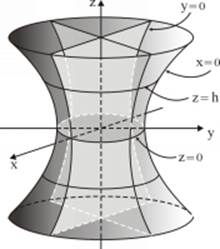
![]()
The hyperboloid is symmetric across coordinate planes ![]() ,
, ![]() ,
, ![]() .
.
The intersection lines of one-sheet hyperboloid with the plane ![]() are ellipse
are ellipse ![]() .
.
If ![]() is increasing, then the ellipses axes are increasing.
is increasing, then the ellipses axes are increasing.
The smallest ellipse, when ![]() , is called the neck of one-sheet hyperboloid.
, is called the neck of one-sheet hyperboloid.
The intersection lines of one-sheet hyperboloid with planes ![]() and
and ![]() are hyperbolas.
are hyperbolas.
8.4 Two-Sheet Hyperboloid
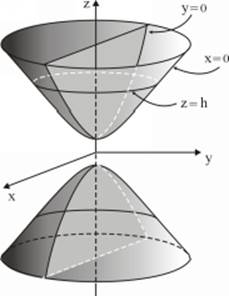
![]()
The canonical form of two-sheet hyperboloid equation indicates it is symmetric across the planes of axes ![]() .
.
The intersection lines of two-sheet hyperboloid with planes ![]() are ellipses.
are ellipses.
Plane ![]() starts intersecting two-sheet hyperboloid for
starts intersecting two-sheet hyperboloid for ![]() . In other words, between planes
. In other words, between planes ![]() and
and ![]() , there exist no points belonging to this surface. The intersection lines with the planes at
, there exist no points belonging to this surface. The intersection lines with the planes at ![]() and
and ![]() are hyperbolas.
are hyperbolas.
8.5 Cone
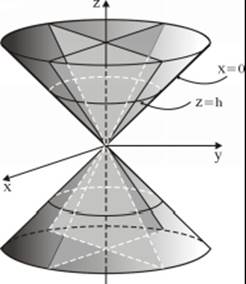
![]()
The intersection lines of cone with planes ![]() are ellipses.
are ellipses.
The intersection line of the cone with plane ![]() are a pair of straight lines
are a pair of straight lines ![]() , and with plane
, and with plane ![]() , are a pair of straight lines
, are a pair of straight lines ![]() .
.
A cone is formed by straight lines passing through the origin.
8.6 Elliptic Paraboloid
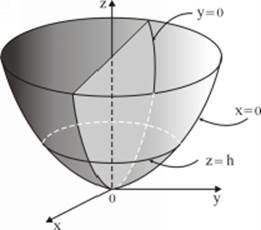
![]()
The intersection lines of elliptic paraboloid with planes ![]() ,
, ![]() are ellipses
are ellipses ![]() that increasingly widen with
that increasingly widen with ![]() increasing.
increasing.
The intersection lines of it with planes ![]() ,
, ![]() are parabolas
are parabolas ![]() and
and ![]() respectively.
respectively.
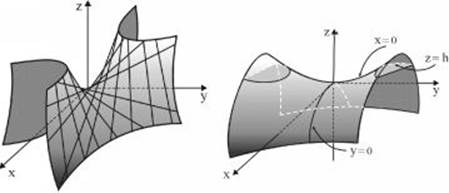
8.7 Hyperbolic Paraboloid
![]() ,
, ![]()
Its intersection lines with planes ![]() are hyperbolas
are hyperbolas ![]() .
.
Its intersection lines with planes ![]() and
and ![]() are parabolas
are parabolas ![]() and
and ![]() respectively.
respectively.
Two straight lines pass through any point in a hyperbolic paraboloid.
8.8 Cylindrical Surface
A cylindrical surface is formed by a straight line moving parallel to given straight line, along a certain curve. Any surface described by one of the equations ![]() (parallel to
(parallel to ![]() -axis),
-axis), ![]() , (parallel to
, (parallel to ![]() -axis),
-axis), ![]() , (parallel to
, (parallel to ![]() -axis) is cylindrical. The following are examples of cylindrical surfaces:
-axis) is cylindrical. The following are examples of cylindrical surfaces:
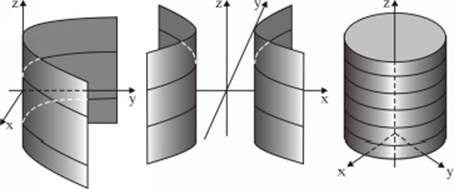
|
Parabolic cylinder
|
Hyperbolic cylinder
|
Elliptic cylinder
|