5 Steps to a 5: AP Physics 2: Algebra-Based 2024 - Jacobs Greg 2023
STEP 4 Review the Knowledge You Need to Score High
9 Fluid Mechanics
IN THIS CHAPTER
Summary: AP Physics 2 includes the study of both static (stationary) and flowing (dynamic) fluids. Keep in mind that the definition of a fluid is anything that flows. This means both a liquid and a gas have fluid behavior, but for the most part you will be dealing with liquids. Entire courses are based on the study of fluid behavior, but in AP Physics 2 you look only at a few relatively simple concepts associated with an idealized, or frictionless, incompressible fluid. Even though the principles may be divided into static and dynamic, a single problem may have both concepts in it.
Key Ideas
The behavior of molecules gives rise to pressure and the forces pressure can produce.
Static fluids—fluids sitting still
(a) Pressure at any point in a fluid is caused by the weight of the column of fluid above that point, plus the pressure acting on the surface of that column of fluid. Therefore, the greater the height of that column, the greater the pressure at the bottom of the column.
(b) Absolute pressure is the difference between the measured pressure and a vacuum. Gauge pressure is the difference between the measured pressure and atmospheric pressure.
(c) “Eureka!” Archimedes’ principle states that the buoyant force on a submerged object is based upon the weight of the displaced fluid.
(d) Pascal’s principle states that any increase in pressure on the surface of a fluid creates an equal and undiminished increase in pressure in all points throughout the fluid.
Dynamic fluids—fluids in motion
(a) Conservation of mass leads us to the continuity equation. Frequently the continuity equation will be needed to determine the speed of a fluid moving through a pipe of changing cross-sectional area. Keep in mind that the continuity equation can be altered to give mass flow rate and volumetric flow rate.
(b) Conservation of energy leads us to Bernoulli’s equation, which is used to relate the velocity, pressure, and height of a flowing fluid from one point in a fluid flow to another.
Relevant Equations
How the Nano-World Influences the Fluid World We Live In
Before we talk about fluids, let’s put on our “nano-glasses” and take a look at the world of the very small to see how the behavior of atoms gives us the behavior of fluids that we experience.
So what causes pressure in a fluid? There are two major causes of pressure.
1. Pressure Due to the Thermal Motion of the Molecules
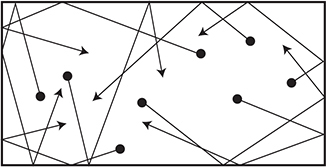
Remember that fluids are made up of lots and lots and lots of molecules. Each of these molecules is vibrating around in a random fashion due to the fluid’s thermal energy. The hotter the fluid, the faster the vibrations of the molecules will be. (More about this in Chapter 10.) These vibrating molecules collide with anything the fluid comes in contact with. The above diagram shows the molecules colliding with the walls of a container. Each collision imparts a small impulse on the wall. Because of the large number of random collisions that occur in every direction, any parallel forces to the wall exerted by the collisions will cancel out! However, the perpendicular component of the collision forces will not cancel out. This means that the forces caused by fluid pressure will always be perpendicular to the surface the fluid is in contact with.
2. Pressure Due to Gravity
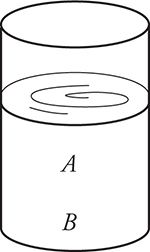
The above diagram shows a stationary liquid in a glass. Since the liquid is stationary, it must be in equilibrium, which means the forces all must be canceling out. Now consider points A and B in the liquid. At each point the forces must cancel out so that they can remain stationary. Each point must support the weight of all the fluid above itself with a counteracting force upward in order to maintain equilibrium. Otherwise the liquid above would accelerate downward due to gravity. Point B has more atoms stacked on top of it than point A does. This means that the pressure from all those molecular collisions at point B must be greater than at point A simply because it has to support more fluid above itself in a gravitational field.
The thermal effect of atomic collisions and the gravitational effect on the atoms combine to cause the overall pressure in a fluid. In gases, the thermal effect causes most of the pressure in a gas. Gases have a very small density, thus the gravitational effect on a gas is very small. The general rule of thumb is that air pressure is assumed to be constant unless there is a lot of vertical height to worry about. Liquids have a much larger density than gases. Thus, the gravitational effect can cause a lot of the pressure in a liquid. Swim just 10 feet to the bottom of a pool and you will notice this pressure increase.
Density
Density is simply the mass per unit volume of an object. In AP Physics 2 you will primarily measure it in kg/m3. You might want to keep in mind that 1 g/cm3 = 1000 kg/m3.
Most of the time, information for density will be given to you in the problem, or there will be enough information given to determine the density of the material. It is a good idea to know the density of water, which is 1000 kg/m3.
Density and Mass
When dealing with fluids, we don’t generally talk about mass—we prefer to talk about density and volume. But, of course, mass is related to these two measurements: mass = density · volume.
So the mass of any fluid equals ρV. And because weight equals mg, the weight of a fluid can be written as ρVg.
Pressure
Pressure is defined as force per unit area:
It is measured in pascals (Pa). One pascal equals one newton per meter squared:
Air pressure, even though it does vary with weather conditions, is given an average value of 100,000 pascals for most AP Physics problems unless otherwise indicated in the problem. This value is listed on the reference table you will be given when taking the AP Physics 2 exam.
With fluids, we talk a lot about pressure, but remember that forces cause things to accelerate. When you need a force, just multiply the pressure times the areas of contact: F = PA.
You need to be aware pressure may be indicated in one of two different ways, absolute pressure and gauge pressure. Absolute pressure is the pressure measured relative to a vacuum, and gauge pressure is the pressure measured relative to atmospheric pressure. So when you measure the gauge pressure in a tire, you are measuring the difference between the pressure in the tire and the atmosphere, or what pressure exists in the tire above that of atmospheric pressure. Absolute pressure means exactly what it sounds like. An absolute pressure of zero describes a complete vacuum. Therefore, absolute pressure equals gauge pressure plus one atmosphere:
Static Fluids
Anybody who has gone swimming at the bottom of a deep swimming pool experiences an increase in pressure as they travel deeper and deeper into the pool. A good way to think about it is as you submerge further into the pool, the column of water above you becomes taller and taller, making the weight of that column of water greater and greater. This increased weight of the column of water corresponds to an increase in pressure at the bottom of that column. Any pressure acting on the surface of that column of water causes an equal, undiminished increase in pressure at all points throughout the fluid; this is known as Pascal’s law. To find the pressure at any point in the fluid:
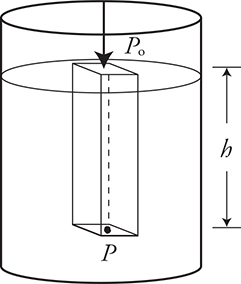
Notice that for a static fluid, the pressure is solely based on the height of the fluid column, the fluid’s density, and the pressure acting on the surface of the column. The shape of the container has no effect. In the diagram below, the pressure is the same in the tube along the bottom, so it supports the same height column of fluid in each container, regardless of the shape of the container.
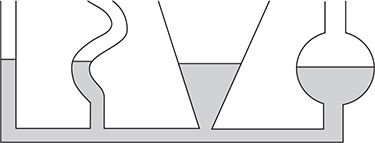
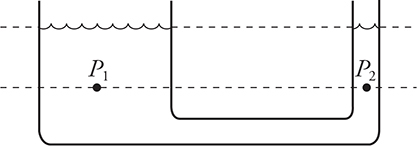
The pressure is the same along any horizontal line drawn through in a stationary connected fluid. In the diagram above, pressure P1 and P2 are the same. Horizontal lines higher in the fluid represent lower pressure. Horizontal lines deeper in the fluid represent higher pressure. The width of the fluid does not matter.
Example
A submarine is at a depth of 300 m in fresh water. If it has a window of 0.10 m radius, what is the force of the water on the window?
First you must keep in mind that you are asked for the actual force of the water on the window, so you need to use absolute pressure when determining the pressure:
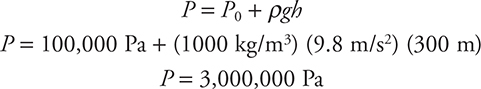
Ignoring the slight height difference from the top and bottom of the vessel’s hull, this pressure is exerted evenly around the entire hull. Since you know the pressure, you can find the force acting on the window.
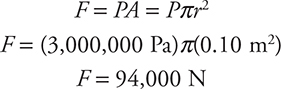
That is like having all of the weight of a good-sized truck pressing on the window so it has to be very thick indeed to withstand that force!
Applications of Static Fluids
This diagram shows a bent tube with liquid inside. The level of the liquid is higher on the left side than the right side. Is it possible for this to happen in a static fluid? There is more than one correct answer, depending on how you explain yourself.
Answer #1: If both sides of the tube are open to the atmosphere, then the answer is no. The left tube has a higher fluid column, which will produce more pressure than at the bottom than the right tube. Therefore, the fluid will flow to the right until the level of fluid is the same in both vertical tubes.
Answer #2: It could be possible to produce different column heights of fluids if the pressures on top of the fluids in the left and right tubes are not the same. The pressure P0 in the right tube would need to be higher.
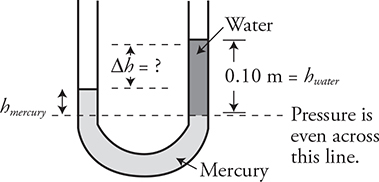
Take a look at this U-tube with two different fluids inside of it and open to the atmosphere on both sides. The fluid is stationary. Since the fluid does not accelerate in one direction or another, you know the forces exerted on the bottom of the U-tube must be equal from both sides of the tube. If this is true, then the pressures exerted on the bottom must be the same from both sides of the tube. When you look at the mercury in the diagram, the pressure, which exists at the mercury-water interface on the right-hand side of the tube, must equal the pressure in the mercury at the same height in the left side of the tube. So that means that the pressure caused by the column of mercury above that height must equal the pressure caused by the column of water on the other side. This makes it relatively easy to find the height of the column of mercury:
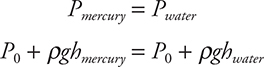
Since P0 and g are the same, you can cancel them out:
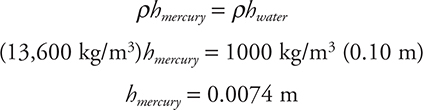
Now it is easy to find the difference in height:
Another application of static pressure is a hydraulic jack. A hydraulic jack consists of two pistons, one with a small area and the other with a large area. If you consider the height of the two pistons to be the same, then the pressure acting on the faces of the pistons will also be the same. When you apply a force to the smaller piston, it yields a larger force on the larger piston due to its larger surface area.
Example
A hydraulic jack is made of two pistons as shown in the next diagram; the smaller piston has an area of 0.01 m2 and the larger one has an area of 0.20 m2. What force would be required to hold up a 1500-N (about 300-lb.) football player?
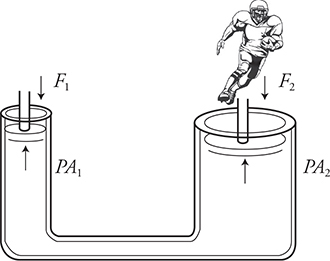
So it takes only 1/20th of the weight of the football player applied to the smaller piston to support the football player.
Barometer
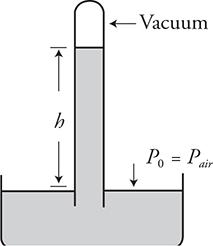
A barometer is a simple device that can measure the pressure acting on the surface of a fluid. A closed-end tube is filled with a fluid (usually water or mercury) and then turned upright inside a container of fluid with the closed end facing upward. The weight of the fluid pulls the fluid down in the tube, creating a vacuum at the top of the tube (Pvacuum = 0). Now, remember that the pressure at the surface of the fluid must be equal at all points at the same horizontal height; therefore, pressure exerted on the surface of the fluid by atmospheric air pressure equals the pressure inside the column of fluid in the tube at the same horizontal level. This pressure on the surface of the mercury holds up the column of mercury in the tube.
Keep in mind that the vacuum in the top of the tube does not “pull” up on the mercury. A vacuum has no pressure, so it cannot apply a force. It is the pressure below that supports the column of mercury in the tube.
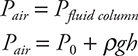
And, since there is a vacuum at the top of the column: P0 = 0.
Buoyancy and Archimedes’ Principle
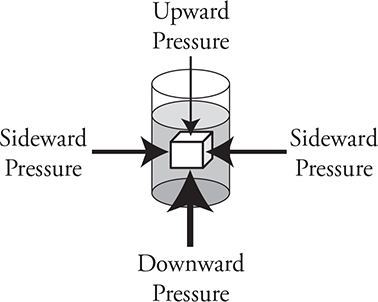
Why do things float? Because there is a gravitational effect on fluids that causes pressure to be greater the deeper you get in a fluid. We know:
1. Pressure in a fluid increases with depth: P = P0 + ρgh.
2. The bottom of the block is deeper in the fluid than the top of the block.
3. Therefore, the upward pressure on the bottom of the block must be greater than the downward pressure on the top of the block.
4. The pressure on the sides of the block must be identical, thus canceling each other out.
5. This means that every object surrounded by a fluid must receive an upward force due to the difference in pressures on the top and bottom of the object!
Do you realize that a helium balloon will not float in the International Space Station? We don’t have the gravity effect pressure in space, only thermal effect pressure, which is the same everywhere in the fluid.
Archimedes discovered the buoyancy principle while taking a bath, so it is named after him—the Archimedes’ principle. According to this principle, when a body is immersed in a fluid either fully or partially, the fluid exerts an upward force on the body equal to the weight of the fluid that is displaced by the body:
Be careful and remember to use the density and volume of the displaced fluid.
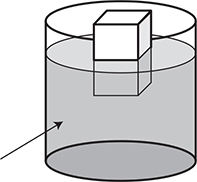
Caution: One common mistake is to assume that the volume of the object is always equal to the volume of the displaced fluid. Objects that float do not necessarily displace the fluid equal to their volume. Only the submerged portion of the object displaces fluid!
Remember Newton’s third law. The fluid is pushing up on the object with a buoyant force. Therefore, the object must be pushing downward on the fluid with an equal but opposite force.
Example
A mass is suspended from a spring scale that reads 5.0 N. When the mass is submerged in water the scale reads 4.2 N. What is the density of the object?
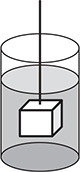
You can ignore the buoyant force of air on the object when it is suspended out of the water because it is very small, so it is simple to find the mass. When out of the water, Newton’s second law gives us:
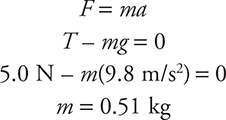
Now apply Newton’s second law when the object is submerged. (Remember to draw your free-body diagram!):
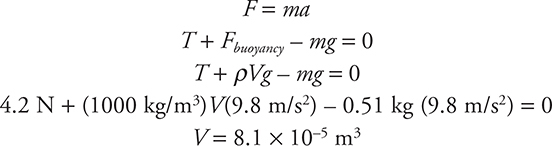
You are all set; you have the mass and the volume:
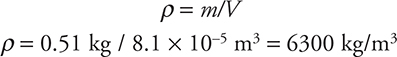
Dynamic Fluids—Continuity
So far we’ve only talked about stationary fluids. But what if a fluid is moving through a pipe? There are two questions that then arise: first, how do we find the velocity of the flow, and second, how do we find the fluid’s pressure? To answer the first question, we’ll turn to the continuity principle. In the next section, we’ll answer the second question using Bernoulli’s equation.
Consider water flowing through a pipe. Imagine that the water always flows such that the entire pipe is full. Now imagine that you’re standing in the pipe1—how much water flows past you in a given time?
We call the volume of fluid that flows past a point every second the volume flow rate, measured in units of m3/s. This rate depends on two characteristics: the velocity of the fluid’s flow, v, and the cross-sectional area of the pipe, A. Clearly, the faster the flow, and the wider the pipe, the more fluid flows past a point every second. To be mathematically precise,
If the pipe is full, then any volume of fluid that enters the pipe must eject an equal volume of fluid from the other end. (Think about it—if this weren’t the case, then the fluid would have to compress or burst the pipe. Once either of these things happens, the principle of continuity is void.) So, by definition, the volume flow rate is equal at all points within an isolated stream of fluid. This statement is known as the principle of continuity. For positions “1” and “2,” for example, we can write A1v1 = A2v2. In reality, continuity is a consequence of conservation of mass. Since no mass is created or destroyed inside the pipe, an equal amount of fluid mass that flows into one end of the pipe must exit out the other end of the pipe.
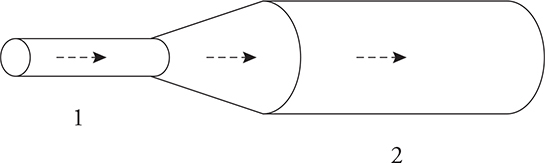
The most obvious physical consequence of continuity is that where a pipe is narrow, the flow is faster. So, the fluid must move faster in the narrower section labeled “1.” Most people gain experience with the continuity principle when using a garden hose. What do you do to get the water to stream out faster? You use your thumb to cover part of the hose opening, of course. In other words, you are decreasing the cross-sectional area of the pipe’s exit, and since the volume flow rate of the water can’t change, the velocity of the flow must increase to balance the decrease in the area.
Dynamic Fluids—Bernoulli’s Equation
Bernoulli’s equation is probably the longest equation you need to know for the AP exam, but fortunately, you don’t need to know how to derive it. What you should know, conceptually, is that it’s really just an application of the conservation of energy.
Bernoulli’s equation is useful whenever you have a fluid flowing from point “1” to point “2.” The flow can be fast or slow; it can be vertical or horizontal; it can be open to the atmosphere or enclosed in a pipe. (What a versatile equation!) P is the pressure of the fluid at the specified point, y is the vertical height at the specified point, ρ is the fluid’s density, and v is the speed of the flow at the specified point.
Too many terms to memorize? Absolutely not! First, we’re dealing with pressures, so obviously there should be a pressure term on each side of the equation. Second, we said that Bernoulli’s equation is an application of energy conservation, so each side of the equation will contain a term that looks kind of like potential energy and a term that looks kind of like kinetic energy. (Note that the units of every term are N/m2.)
Principal Consequence of Bernoulli’s Equation
The most important result that can be derived from Bernoulli’s equation is this: generally, where flow is faster, pressure is lower.
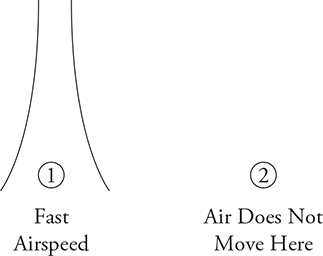
Take two pieces of paper and hold them parallel to each other, a couple centimeters apart. Now get someone with strong lungs—a trombone player, perhaps—to blow a fast, focused stream of air between the sheets of paper. He will blow the sheets apart, right?
No! Try the experiment yourself! You’ll see that the pieces of paper actually move together. To see why, let’s look at the terms in Bernoulli’s equation.2 Take point “1” to be between the sheets of paper; take point “2” to be well away from the sheets of paper, out where the air is hardly moving, but at the same level as the sheets of paper so that y1 and y2 are the same. (See the diagram above.) We can cancel the y terms because they are at the same height and solve for the pressure between the sheets of paper:
Far away from the pieces of paper, the air is barely moving (so v2 is just about zero), and the pressure P2 must be the ambient atmospheric pressure. But between the sheets, the air is moving quickly. So look at the terms in parentheses: v1 is substantially bigger than v2, so the part in parentheses gives a negative quantity. This means that to get P1, we must subtract something from atmospheric pressure. The pressure between the pieces of paper is less than atmospheric pressure, so the air on the exterior of both pieces of paper push the pieces of paper together.
This effect can be seen in numerous situations. A shower curtain is pushed in toward you when you have the water running past it; an airplane is pushed up when the air rushes faster over top of the wing than below the wing; a curveball curves because the ball’s spin causes the air on one side to move faster than the air on the other side.
In general, solving problems with Bernoulli’s equation is relatively straightforward. Yes, the equation has six terms: one with pressure, one with height, and one with speed for each of two positions. But in almost all cases you will be able to get rid of several of these terms, either because the term itself is equal to zero, or because it will cancel with an identical term on the other side of the equation. For example:
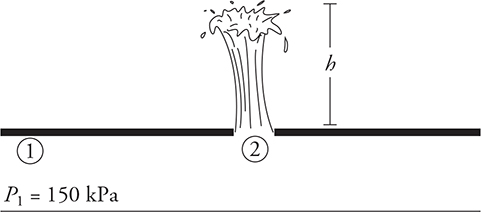
In a town’s water system, pressure gauges in still water at street level read 150 kPa. If a pipeline connected to the system breaks and shoots water straight up, how high above the street does the water shoot?
We know that we should use Bernoulli’s equation because we are given the pressure of a flowing fluid, and we want to find the speed of the flow. Then, kinematics can be used to find the height of the fountain.
Let point “1” be in still water where the 150 kPa reading was made, and point “2” will be where the pipe broke. Start by noting which terms in Bernoulli’s equation will cancel: both points are at street level, so y1 = y2 and the height terms go away; the velocity at point “1” is zero because point “1” is in “still” water.
Now the pressure terms: If a gauge reads 150 kPa at point “1,” this is obviously a reading of gauge pressure, which you recall means the pressure over and above atmospheric pressure. The pressure where the pipe broke must be atmospheric.
Of the six terms in Bernoulli’s equation, we have gotten rid of three:
This leaves
P1 is equal to Patm + 150 kPa; P2 is just atmospheric pressure:
The atmospheric pressure terms go away. Plug in the density of water (1000 kg/m3), change 150 kPa to 150,000 Pa, and solve for velocity:
Finally, we use kinematics to find the height of the water stream. Start by writing out the table of variables; then use the appropriate equation.
x — x0 = 15 m high, about the height of a four- or five-story building.
Real-World Examples of Bernoulli
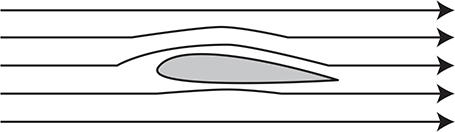
Wings and lift: The shape of the airfoil compresses the flow tube about the wing. This increases the velocity of the air above the wing, creating a pressure difference between the top and bottom of the wing, producing lift.
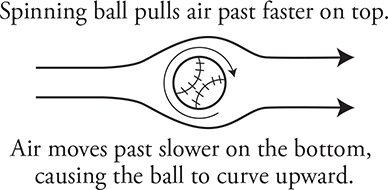
Curveball: Friction between the ball and the air causes the ball to drag the air faster past itself on one side while hindering the airflow on the other side. This velocity difference creates a pressure difference and curves the trajectory of the ball. (Try it with a beach ball or Ping-Pong ball!)
Beach ball trapped above a fan: Position a fan so that it blows air upward. Now release a beach ball in the airstream. When the ball tries to escape from the airstream it will encounter high-pressure stationary air that pushes the ball back into the low-pressure airstream. You can do this with a leaf blower and a tennis ball. Tape a string to a Ping-Pong ball and swing it into a stream of water from a faucet to get the same effect!
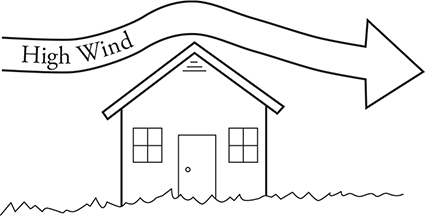
High winds blowing a roof off: During storms, high winds move past the roof of a house dropping the pressure of the air above the roof. The stationary air inside the house has a higher pressure that can literally blow the roof off the house!
❯ Practice Problems
Multiple Choice
1. A dam holds water in a lake that extends 1000 m east of the dam. If it extended 2000 m east instead of 1000 m, the pressure at the base of the dam would:
(A) increase
(B) decrease
(C) remain the same
2. A horizontal 4-cm diameter pipe tapers to a 2-cm nozzle. If the water emerges from the nozzle at 20 m/s, what is the pressure in the 4-cm diameter section of the pipe?
(A) 107,500 Pa
(B) 190,000 Pa
(C) 250,000 Pa
(D) 290,000 Pa
3. A pirate ship hides out in a small inshore lake. It carries 20 ill-gotten treasure chests in its hold. But lo, on the horizon the lookout spies a gunboat. To get away, the pirate captain orders the heavy treasure chests jettisoned. The chests sink to the lake bottom. What happens to the water level of the lake?
(A) The water level drops.
(B) The water level rises.
(C) The water level does not change.
4. Manny saves 2-liter soda bottles so that he can construct a raft and float out onto the Trinity River. If Manny has a mass of 80 kg, what minimum number of bottles is necessary to support him? The density of water is 1000 kg/m3, and 1000 L = 1 m3.
(A) 1600 bottles
(B) 800 bottles
(C) 200 bottles
(D) 40 bottles
(E) 4 bottles
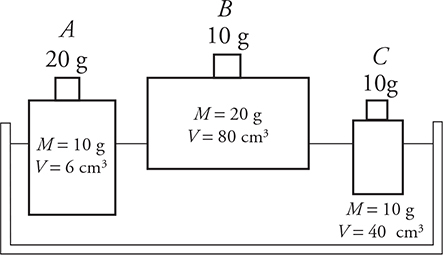
5. Three plastic blocks of different masses and volumes float with weights on top of them. Which of the following correctly ranks the buoyancy force on the plastic blocks?
(A) A = B > C
(B) A > B = C
(C) B > A > C
(D) B > A = C
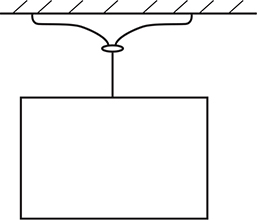
6. A suction cup is used to hang a sign from the ceiling as shown above. Which of the following statements is correct?
(A) The force from the air upward on the suction cup is greater than the weight of the suction cup and sign.
(B) The pressure of the air upward on the suction cup is equal to the weight of the suction cup and the sign.
(C) The difference in pressure between the inside and outside of the suction cup equals the weight of the suction cup and the sign.
(D) The low pressure inside the suction cup pulls the suction cup upward and holds the sign up, canceling gravity.
Questions 7 and 8
Four differently shaped sealed containers are completely filled with an unknown fluid, as shown in the figure below. Containers A and B are cylindrical. Containers C and D are truncated conical shapes. The top and bottom diameters of the containers are shown below.
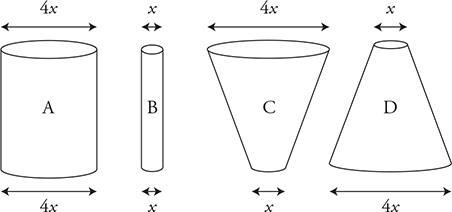
7. Which of the following is the correct ranking of the pressure (P) at the bottom of the containers?
(A) PA = PB = PC = PD
(B) PA = PD > PC = PB
(C) PA > PD > PC > PB
(D) PD > PA > PC > PB
8. The force on the bottom of container A due to the fluid inside the container is F. What is the force on the bottom of container B due to the fluid inside?
(A) F
(B) F/4
(C) F/8
(D) F/16
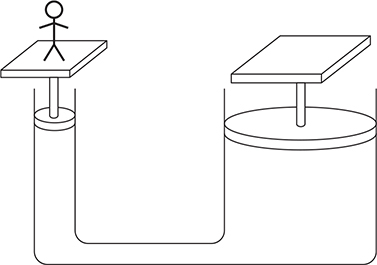
9. Two cylinders filled with a fluid are connected by a pipe so that fluid can pass between the cylinders, as shown in the figure above. The cylinder on the right has 4 times the diameter of the cylinder on the left. Both cylinders are fitted with a movable piston and a platform on top. A person stands on the left platform. Which of the following lists the correct number of people that need to stand on the right platform so neither platform moves? Assume that the platform and piston have negligible mass and that all the people have the same mass.
(A) 16 people
(B) 4 people
(C) 1 person
(D) It is impossible to balance the system because you need 1/16 of a person on the right side
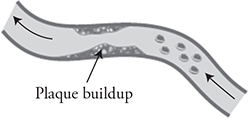
10. Blood cells pass through an artery that has a buildup of plaque along both walls, as shown in the figure. Which of the following correctly describes the behavior of the blood cells as they move from the right side of the figure through the area of plaque? Assume the blood cells can change volume.
(A) The blood cells increase in speed and expand in volume.
(B) The blood cells increase in speed and decrease in volume.
(C) The blood cells decrease in speed and expand in volume.
(D) The blood cells decrease in speed and decrease in volume.
Free Response
11. A person sips a drink from a straw.
(A) Rank the pressure inside the person’s mouth A, to the pressure at the surface of the drink B, to the pressure at the bottom of the drink C. Justify your response.
(B) Explain using words how the person is able to drink from a straw.
(C) Justify your explanation in (B) by using a derivation.
(D) The top of the drink is now sealed with an air-tight lid. What affect will this have on the person drinking?
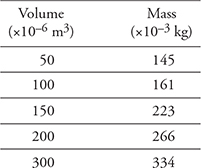
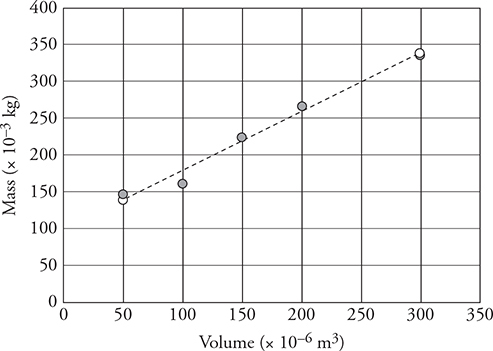
12. Your teacher has asked you to determine the density of a liquid. You place a graduated cylinder on a balance and measure the mass at different volumes. The data is displayed in the table above.
(A) Graph the data appropriately on the grid provided to the right.
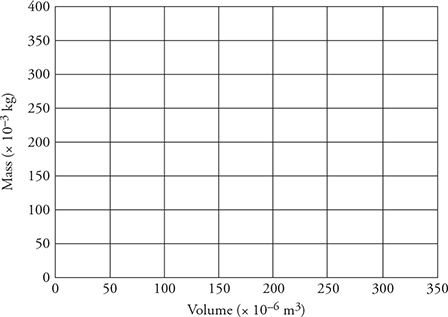
(B) Explain why the best fit line does not go through the origin and explain what the intercept represents.
(C) Use the graph to determine the density of the fluid in kg/m3. Show your work.
(D) How might you improve the accuracy of the lab?
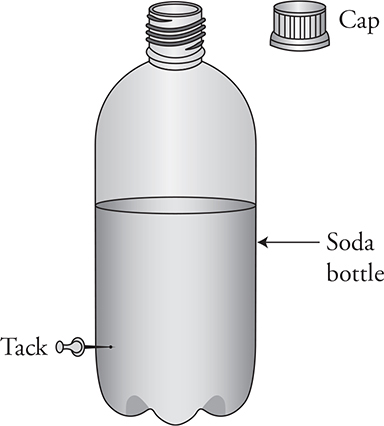
13. A soda bottle is filled partway with water. A tack is poked into the side to create a hole. The cap is removed from the bottle.
(A) When the tack is removed, water flows out. As the water level descends, the velocity of the water leaving the hole decreases. Explain why this happens in terms of pressure and energy.
(B) The bottle is refilled to its original level, and the tack is used to plug up the hole. The cap is tightened, and the tack is again removed. Water comes out of the hole but quickly stops while there is still a large quantity of water above the tack hole. Explain why this occurs.
14. The force on the bottom of a swimming pool must increase when a person is floating in the pool. Explain this behavior
(A) using Newton’s third law.
(B) by referencing the water level in the pool.
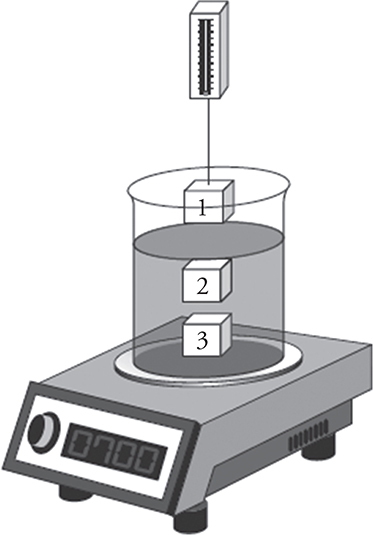
15. A beaker of water rests on an electronic balance, as shown in the figure above. A mass suspended from a spring scale is lowered into the water. Location 1 is above the water. Location 2 is just below the surface of the water. Location 3 is just above the bottom of the beaker.
(A) Do the spring scale and balance readings increase, remain the same, or decrease when the mass is lowered from location 1 to location 2? Explain.
(B) Do the spring scale and balance readings increase, remain the same, or decrease when the mass is lowered from location 2 to location 3? Explain.
16. A hose with a 2-cm radius supplies water to fill a pool. Water flows out of the hose at a rate of 6 m/s. The pool has a length of 12 m, a width of 9 m, and a depth of 2 m.
(A) What is the volume flow rate of the water exiting the hose?
(B) How many hours does it take to completely fill the pool?
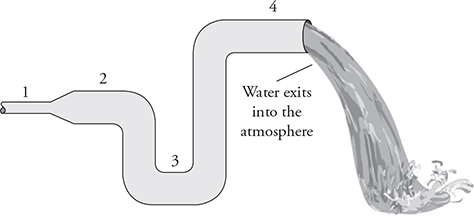
17. Water passes through a closed piping system starting at point 1 and exits to the atmosphere at the highest point near point 4. The pipe has a small diameter at point 1 but then widens out to a larger constant radius for the rest of the pipe.
(A) Rank the velocity of the water in the pipe at the four locations from greatest to least. Justify your answer.
(B) Rank the pressure in the pipe at the four points from greatest to least. Justify your answer.
❯ Solutions to Practice Problems
1. (C) The pressure in a fluid is based upon the height of the column of fluid, the density of the fluid, and pressure exerted on the surface of the fluid. By extending the horizontal dimension of the lake, you are not changing any of these variables, so the pressure remains the same.
2. (D) This is a combination Continuity and Bernoulli’s equation problem. The pressure acting on the fluid exiting the pipe is air pressure, so your pressure at this point is atmospheric—100,000 Pa. You will need to find the flow velocity at the wider section of the pipe so you will use the continuity equation:
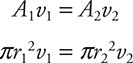
You can cancel π out from both sides and have to remember to change your diameters to radii.
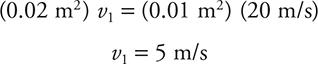
Now that you have the velocity at the narrow section, you can apply Bernoulli’s equation.
Consider the nozzle point 1 and the wide section point 2. Since the pipe is horizontal, there is no change in height, so the height can be considered zero and those terms can drop out. You are left with:
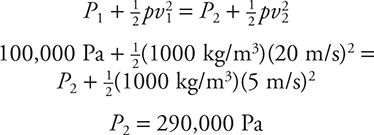
3. (A) When the treasure is floating in the boat, it displaces an amount of water equal to its weight. When the treasure is on the lake bottom, it displaces much less water, because the lake bottom supports most of the weight that the buoyant force was previously supporting. Thus, the lake level drops.
4. (D) Since Manny will be floating in equilibrium, his weight must be equal to the buoyant force on him. The buoyant force is ρwaterVsubmergedg, and must equal Brian’s weight of 800 N. Solving for Vsubmerged, we find he needs to displace 8/100 of a cubic meter. Converting to liters, he needs to displace 80 L of water, or 40 bottles. (We would suggest that he use, say, twice this many bottles—then the raft would float only half submerged, and he would stay drier.)
5. (A) Since all the objects are floating, the buoyancy force must equal the weight of the combined objects.
6. (A) Pressure is not a force and cannot equal or cancel out the gravity force. Assuming there is still air inside the suction cup, the force from the external air upward would need to be larger than the overall weight to cancel out the extra force from the air still inside the suction cup pushing down from the inside. Even if there was a vacuum inside the suction cup, the force from the air would be greater than the weight of the system as there would be a normal force pushing downward on the suction cup from the ceiling.
7. (A) They are all the same: P = P0 + ρgh
8. (D) The pressure is the same at the bottom of each container. The area of the bottom surface =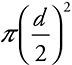 
. Thus the force at the bottom on the container is 
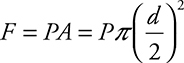. Inserting the diameter of each container, we see that the force on the smaller container is 1/16 that of the larger container.
9. (A) The pressure at the top of both pistons must be the same:
10. (A) The speed increases as it passes through the region of plaque and, as shown by Bernoulli’s equation, the pressure in the fluid decreases. Thus, the cell will increase in size.
11. (A) PC > PB > PA. The pressure at the bottom of the drink is the highest due to the column of fluid above it and the atmosphere above that. The pressure at the top of the drink is atmospheric. The pressure inside the person’s mouth must be less than atmospheric so that fluid rises up the straw.
(B) The person must lower the pressure inside his or her mouth. Then, the higher pressure at the bottom of the straw pushes fluid up toward the person’s mouth where the pressure is lower. (Note that the person does not “suck” the drink up to his or her mouth!)
(C)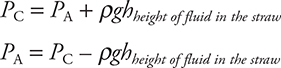 
(D) As the fluid moves up the straw, it reduces the amount of fluid in the cup. When the lid is airtight, this increases the volume of “the air pocket” at the top of the cup, which will reduce the pressure in this air pocket. This will in turn reduce the pressure of the fluid at the bottom of the drink. This makes it harder for the person to produce the pressure differential to push fluid up the straw and drink.
12. (A) See the graph.
(B) You forgot to tare the balance. The intercept is the mass of the graduated cylinder (approximately 100 g).
(C) The density of the fluid equals the slope of the best fit line of the data. The slope is about 800 kg/m3.
(D) More data points over a wider range almost always helps. Taring the balance won’t really help because the slope of the line is independent of the mass of the graduated cylinder.
13. (A) The water pressure at the hole is determined by the height of the water above the hole. As the amount of water decreases, the pressure that pushes the water out of the hole decreases as well. In terms of energy, think of the amount of fluid above the tack as gravitational potential energy that can be converted to kinetic energy in the water exiting the tack hole. As the water level descends, the gravitational potential energy decreases, which decreases the kinetic energy of the exiting water.
(B) When the water level descends, the air pocket at the top of the bottle increases. With the cap on the bottle, air from the outside cannot flow in. The ideal gas law, PV = nRT, tells us that as the volume of air above the water increases, the pressure of that air must decrease. The static pressure equation, P = P0 + ρgh, tells us that as the pressure on top of the water decreases, the water pressure at the tack hole will also decrease. Eventually, the water pressure inside the bottle equals the air pressure outside the bottle, and we have equilibrium. The water stops coming out of the tack hole.
14. (A) When a person floats in a pool, he or she receives a buoyancy force from the water. By Newton’s third law, the water must also receive an equal and opposite force downward from the person. This downward force increases the force on the bottom of the pool.
(B) When a person floats in a pool, he or she displaces water, which makes the water level rise. This rise in water height causes an increase in the static fluid pressure on the bottom of the pool, which in turn increases the force on the bottom of the pool.
15. (A) The spring scale reading decreases because the buoyancy force pushes up on the mass. The balance reading increases because the mass pushes down on the water with a Newton’s third law force that is equal in magnitude but opposite in direction to the upward buoyancy force on the mass.
(B) Both scales’ readings remain the same. The object does not displace any additional water moving from position 2 to position 3. Therefore, the buoyancy force does not change by moving the mass from position 2 to position 3.
16. (A)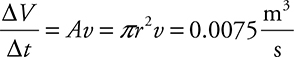 
. Remember to convert your units!
(B) The volume of the pool is 216 m3. Divide the volume of the pool by the volume flow rate, and you get 28,800 seconds to fill the pool, which is 8 hours.
17. (A) Continuity tells us that the velocity of the water is fastest at location 1 and is uniformly slower at locations 2, 3, and 4.
(B) There is a lot going on here.
• Continuity tells us that the speed is slower at locations 2, 3, and 4.
• Bernoulli tells us that the slower the fluid moves, the higher the pressure. This means the pressure at location 2 is higher than at location 1.
• Static pressure tells us that the lower the pipe is, the higher the pressure. This means that in the large pipe, location 3 has the highest pressure and location 4 has the lowest.
• Combining all these considerations, we can see that the pressure is highest at location 3 followed by location 2. It is impossible to compare locations 1 and 4 accurately without more information about the pipe diameters and the height difference between location 1 and 4. We just know the pressures at locations 1 and 4 are both lower than at location 2.
❯ Rapid Review
• Pressure is caused by the random thermal motion of the molecules.
• Gravitational force pulling fluids downward increases pressure. The deeper inside a fluid you go, the higher the pressure gets.
• The force caused by pressure is always perpendicular to the surface of contact.
• Pressure equals force divided by the area over which the force is applied.
• Density equals the mass of a substance divided by its volume.
• The absolute pressure exerted by a column of a fluid equals the pressure at the top of the column plus the gauge pressure—which equals ρgh.
• The buoyant force on an object is equal to the weight of the fluid displaced by that object.
• If a force is applied somewhere on a container holding a fluid, the pressure increases everywhere in the fluid, not just where the force is applied.
• The volume flow rate—the volume of fluid flowing past a point per second—is the same everywhere in an isolated fluid stream. This means that when the diameter of a pipe decreases, the velocity of the fluid stream increases, and vice versa.
• Bernoulli’s equation is a statement of conservation of energy. Among other things, it tells us that when the velocity of a fluid stream increases, the pressure decreases.
1Wearing a scuba mask, of course.
2Yes, Bernoulli’s equation can be applied to gases as well as liquids, as long as the gas is obeying the continuity principle and not compressing. This is a good assumption in most cases you’ll deal with on the AP exam.