5 Steps to a 5: AP Physics 2: Algebra-Based 2024 - Jacobs Greg 2023

STEP 2 Determine Your Test Readiness
4 Test Yourself: AP Physics 2 Fundamentals

IN THIS CHAPTER

Summary: This chapter contains a basic concepts quiz for AP Physics 2 designed to help you judge your areas of genius and areas of need.

Key Ideas

Discover which topics you know and don’t know from the AP Physics 2 content.

Use this self-evaluation quiz to help guide you in constructing your study plan from Chapter 3.

AP Physics 2 Fundamentals Self-Assessment

The questions in this chapter are not written in the AP exam style. This is just a quiz. It’s really a bunch of rapid-fire questions. They are designed to get a quick idea of what you know cold, what is fuzzy, and what is absent from your brain. So rifle through the questions, answering as many as you can. Check your answers with the key at the end. Based on your results, you should now know your content strengths and weaknesses. Return to Chapter 3 with this knowledge and build your study plan.

Fluids

1. How would you determine the density of an object?

2. What is the physical mechanism in a fluid that causes a force on a surface? We are not looking for an equation here!

3. Mathematically how do you calculate force knowing the pressure? OK, now we are looking for an equation.

4. For the equation P = P₀ + ρgh,

(a) for what kind of situation is the equation valid?

(b) what does P₀ stand for (careful!)?

5. Write Bernoulli’s equation.

6. State Archimedes’ principle in words by finishing the following sentence: “The buoyant force on an object in a fluid is equal to . . .”

7. For a flowing fluid, what quantity does Av represent, and why is this quantity the same everywhere in a flowing fluid?

8. Write the alternate expression for mass that is useful when dealing with fluids of known density.

Thermal Physics, Thermodynamics, and Gases

9. How do you determine the internal energy of a gas given the temperature of the gas? Define all variables in your equation.

10. How do you determine the rms speed of molecules given the temperature of a gas? Define all variables in your equation.

11. State the equation for the first law of thermodynamics. What does each variable stand for? What are the units of each term?

12. Sketch two isotherms on the PV diagram below. Label which isotherm represents the higher temperature.

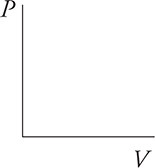
13. Describe a situation in which heat is added to a gas, but the temperature of the gas does not increase.

14. Imagine you are given a labeled PV diagram for 1 mole of an ideal gas. Note that one of the following is a trick question!

(a) How do you use the graph to determine how much work is done on or by the gas?

(b) How do you use the graph to determine the change in the gas’s internal energy?

(c) How do you use the graph to determine how much heat was added to or removed from the gas?

15. How can we estimate absolute zero in a school lab?

16. If the volume of a gas doubles while the temperature is held constant, what happens to the pressure of the gas?

17. Heat is added to a gas in a closed rigid container.

(a) Is there any work done by or on the gas?

(b) What happens to the temperature and pressure of the gas?

18. Why does heat always flow from hot objects to cold objects?

19. What are the three ways heat can be transferred? Explain each process.

Static Electricity, Circuits, and Magnetism

20. Given the charge of a particle and the electric field experienced by that particle, give the equation to determine the electric force acting on the particle.

21. Given the charge of a particle and the magnetic field experienced by that particle, give the equation to determine the magnetic force acting on the particle.

22. A wire carries a current to the left, as shown below. What is the direction and magnitude of the magnetic field produced by the wire at point P ?

23. When is the equation kQ/r² valid? What is this an equation for?

24. The electric field at point P is 100 N/C; the field at point Q, 1 meter away from point P, is 200 N/C. A point charge of +1 C is placed at point P. What is the magnitude of the electric force experienced by this charge?

25. Can a current be induced in a wire if the flux through the wire is zero? Explain.

26. True or false: In a uniform electric field pointing to the right, a negatively charged particle will move to the left. If true, justify with an equation; if false, explain the flaw in reasoning.

27. Which is a vector and which is a scalar: electric field and electric potential?

28. Fill in the blank with either “parallel” or “series”:

(a) Voltage across resistors in ______ must be the same for each.

(b) Current through resistors in ______ must be the same for each.

(c) Voltage across capacitors in ______ must be the same for each.

(d) Charge stored on capacitors in ______ must be the same for each.

29. A uniform electric field acts to the right. In which direction will each of these particles accelerate?

(a) proton

(b) positron (same mass as electron, but opposite charge)

(c) neutron

(d) anti-proton (same mass as proton, but opposite charge)

(e) electron

30. A uniform magnetic field acts to the right. In which direction will each of these particles accelerate, assuming they enter the field moving toward the top of the page?

(a) proton

(b) positron (same mass as electron, but opposite charge)

(c) neutron

(d) anti-proton (same mass as proton, but opposite charge)

(e) electron

31. How do you find the potential energy of an electric charge?

32. Describe the processes of conduction, polarization, and induction.

33. What is the smallest unit of charge that you will likely ever find? Why?

34. What do the electric field and electric potential “look like” between two oppositely charged capacitor plates?

35. The force between two charges is F. If the magnitude of both the charges is doubled and the charges are moved twice as far apart, what will be the new force?

36. What are the similarities and differences between the electric force and gravitational force?

37. Two identical metal spheres, one with a charge of +2 C and the other with a charge of −4 C, touch. What is the new charge of each sphere?

38. If you double the diameter of a wire, what happens to its resistance?

39. How would you determine if a resistor is ohmic?

40. I want to increase the capacitance of a capacitor. How could I change the geometry of the capacitor to accomplish this?

41. An uncharged capacitor is connected to a battery. Compare the current of an uncharged capacitor immediately after it is connected to a battery to its current after it has been connected for a long time. Explain.

42. Describe how ferromagnetic, paramagnetic, and diamagnetic materials behave when placed in an external magnetic field.

Physical and Geometric Optics

43. Describe what each variable means in the equation d sin θ = mλ.

44. Describe how the interference pattern for a single slit is the same and different from an interference pattern for a double slit where the width of the single slit is the same as the distance between the centers of the double slits.

45. Explain how dark and light locations are created when light shines through a double slit.

46. Describe the differences between electromagnetic and mechanical waves.

47. Only 80% of the light that strikes a particular surface reflects from it. What happened to the rest of the light?

48. Why does light refract (bend) when it enters a new medium?

49. (a) When light travels from water (n = 1.3) to glass (n = 1.5), which way does it bend?

(b) When light travels from glass to water, which way does it bend?

(c) In which of the above cases may total internal reflection occur?

(d) Write (but don’t solve) an equation for the critical angle for total internal reflection between water and glass.

50. Describe two principal rays drawn for a convex lens. Be careful to distinguish between the near and far focal points.

1.

2.

51. Describe two principal rays drawn for a concave lens. Be careful to distinguish between the near and far focal points.

1.

2.

Quantum, Atomic, and Nuclear

52. After sitting on a shelf for 3 years, a radioactive sample has only one-eighth of its original beta particle emissions. What does this tell you about the sample?

53. Green light shines on a photosensitive material, causing it to eject electrons.

(a) What can you do to cause more electrons to be ejected?

(b) What can you do to cause the ejected electrons to have more energy?

54. What conservation laws are obeyed in the nano-world?

55. A photon collides with a stationary electron giving it a velocity. What has happened to the wavelength and frequency of the photon? Explain.

56. Why does gas in a neon bulb emit only discrete wavelengths of light?

57. What does a wave function tell us?

58. Uranium decays into thorium by ejecting an alpha particle. How does the mass of the uranium compare to the thorium and alpha particle? Explain.

59. We often use two different equations for wavelength:

When is each used?

60. Name the only decay process that affects neither the atomic number nor the atomic mass of the nucleus.

Answers to AP Physics 2 Fundamentals Self-Assessment

1. ρ = m/V. So, all we need to do is find mass and volume. Mass can be found using a balance. If the object has a geometric shape, measure it with a ruler and calculate its volume. If it is irregular, fill a container to the rim with water. Submerge the object, and collect and measure the overflow volume of water.

2. The simple answer is pressure, but what causes the pressure? Fluids are made of a bajillion tiny molecules in constant random motion. These individual molecules are colliding with and recoiling from any surface touching the fluid. This imparts an individual molecular impulse to the surface that is perpendicular to that surface. Add up all these individual impulses and you get pressure.

3. F = PA. Remember that the force caused by fluid pressure is always perpendicular to the surface.

4. (a) This is valid for a static (not moving) column of fluid.

(b) P₀ stands for pressure at the top of the fluid; not necessarily, but sometimes, atmospheric pressure.

5.

6. . . . the weight of the fluid displaced.

7. Av is the volume flow rate. The volume of fluid remains constant, so the total volume flowing past one point in a second must push the same amount of total volume past another downstream point in the same time interval.

8. mass = density · volume

9. . Internal energy is times the number of molecules in the gas times Boltzmann’s constant (which is on the constant sheet) times the absolute temperature, in kelvins. Or, RT is correct, too, because Nk_B = nR. (Capital N represents the number of molecules; small n represents the number of moles.)

10.

k_B is Boltzmann’s constant, T is absolute temperature in kelvins, and m is the mass of each molecule in kilograms (NOT in amu!). This can also be expressed as where m is the molar mass of the gas and R is the ideal gas constant.

11. ΔU = Q + W

Change in internal energy is equal to (say it in rhythm, now) “heat added to, plus work done on” a gas. Each term is a form of energy and so has units of joules.

12. The isotherm labeled as “2” is at the higher temperature because it has a higher pressure times volume number (higher PV value).

13. Let’s put a sealed piston filled with room-temperature gas into a boiling water bath, adding heat. But let’s also make the piston on the gas cylinder expand, so that the gas does work. By the first law of thermodynamics, if the gas does as much or more work than the heat added to it, then ΔU will be zero or negative, meaning the gas’s temperature stayed the same or went down.

14. (a) Find the area under the graph. (b) Use PV = nRT to find the temperature at each point; then, use to find the internal energy at each point; then subtract to find ΔU. (c) You can NOT use the graph to determine heat added or removed. The only way to find Q is to find ΔU and W and use the first law of thermodynamics.

15. An estimate for absolute zero can be found by plotting the relationship between gas pressure and its temperature while keeping the volume constant. For example, confine a gas in a container. While measuring the temperature and pressure, cool the gas. Plot the data and you will see that as temperature goes down, pressure goes down (a linear relationship). Draw a line through your data and extrapolate backward until you get to zero pressure, because you can’t go any lower than no pressure. The temperature at zero pressure is absolute zero.

You can also find absolute zero by measuring gas volume as a function of temperature and repeating the extrapolation process to zero volume. The temperature at zero volume is absolute zero.

16. The model for an ideal gas is PV = nRT. Temperature is being held constant, R is a constant, and assuming we don’t gain or lose any gas in the process, the number of moles is a constant. Therefore: PV = a constant. So, if volume doubles, the pressure will be cut in half.

17. Heat is added (+Q). The volume of the container does not change (ΔV = 0):

(a) W_donebygas = PΔV = 0.

(b) ΔU = Q + W. Since work is zero and heat is positive, the internal energy of the gas goes up. From the kinetic theory of gases, we know that the internal energy of a gas is directly related to the temperature of the gas. Therefore, as ΔU goes up, so does temperature. Finally, from the ideal gas law PV = nRT, we see that volume and the number of molecules aren’t changing. Pressure is directly related to temperature. Therefore, the pressure increases as well.

18. Objects are made up of a bajillion atoms moving in a distribution of random speeds. Some fast, some slow. Temperature measures the average motion of these atoms. In hotter objects, on average, the atoms are moving faster. If you put a hot object in contact with a cold object, on average, the faster-moving atoms in the hot object will transfer energy to the slower-moving ones in the cold object by elastic collisions.

19. Conduction is a process by which thermal energy is transferred by physical contact from atom to atom as we just discussed in #18. Convection is a process of thermal energy transfer through the movement of hot fluids as they rise due to changes in density. Radiation is the emission of electromagnetic radiation due to the random vibration of the charged particles. The higher the temperature of the object, the faster the particles vibrate and the more they radiate energy at higher frequencies.

20. F = qE

21. F = qvB sin θ

22. Point your right thumb in the direction of the current (i.e., to the left). Your fingers point in the direction of the magnetic field. This field wraps around the wire, pointing into the page above the wire and out of the page below the wire. Since point P is below the wire, the field points out of the page.

23. This equation is only valid when a point charge or spherical charge distribution produces an electric field. It is an equation for the electric field produced by the point charge or spherical charge distribution.

24. Do not use E = kQ/r² here, because the electric field is known. So, the source of the electric field is irrelevant—just use F = qE to find that the force on the charge is (1 C)(100 N/C) = 100 N. (The charge is placed at point P, so anything happening at point Q is irrelevant.)

25. Yes! Induced emf depends on the change in flux. So, imagine that the flux is changing rapidly from one direction to the other. For a brief moment, flux will be zero; but flux is still changing at that moment. (And, of course, the induced current will be the emf divided by the resistance of the wire.)

26. False. The negative particle will be forced to the left. But the particle could have entered the field while moving to the right . . . in that case, the particle would continue moving to the right, but would slow down.

27. Electric field is a vector, so fields produced in different directions can cancel. Electric potential is a scalar, so direction is irrelevant.

28. Voltage across resistors in parallel must be the same for each.

Current through resistors in series must be the same for each.

Voltage across capacitors in parallel must be the same for each.

Charge stored on capacitors in series must be the same for each.

29. The positively charged proton will accelerate with the field, to the right.

The positively charged positron will accelerate with the field, to the right.

The uncharged neutron will not accelerate.

The negatively charged anti-proton will accelerate against the field, to the left.

The negatively charged electron will accelerate against the field, to the left.

30. Use the right-hand rule for each:

The positively charged proton will accelerate into the page.

The positively charged positron will accelerate into the page.

The uncharged neutron will not accelerate.

The negatively charged anti-proton will accelerate out of the page.

The negatively charged electron will accelerate out of the page.

31. If you know the electric potential experienced by the charge, PE = qV.

32. Conduction is when a charged object is physically touched to another. The charge migrates between the objects, and the two share the original net charge. Polarization is when you bring a charged object close to, but not touching, something else. The charged object repels like charges and attracts opposite charges in the second object, causing it to have a charge separation, but not a net charge. One side becomes more positive, and the other side becomes more negative. Induction is one step beyond polarization. With induction, the charged object is brought close to, but does not touch, a second object. This creates a charge separation—polarization. Now an escape path, or “ground,” is attached to the polarized object, which allows the repelled charge to escape. The ground is removed, and the object is now charged the opposite sign.

33. 1.6 × 10^—19 C. This is the charge of an electron/proton. Unless you have a particle accelerator in your classroom, this is the smallest unit of charged matter you will ever encounter. Everything else you will encounter is made up of protons and electrons, so 1.6 × 10^—19 C is the smallest you will see.

34. The electric field will be uniform in strength and direction, pointing away from the positive plate and toward the negative one. The electric potential will have isolines that are parallel to the capacitor plates (making them perpendicular to the E-Field lines). Near the edges of the capacitor plates, things begin to get “curvy” as E-Field and isolines of potential spill out.

35. 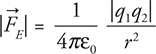Double both charges and double the radius and you get 4 on top and 4 on the bottom, which cancel: 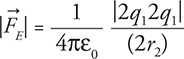. Thus the force stays the same.

36. 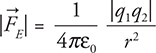versus

Similarities: both have the same inverse squared relationship with the radius. Both exert a force on a line between the two objects. Both forces extend to infinity. Differences: mass is always positive, while charge can be negative or positive. Gravity only attracts, while electric force attracts and repels. Gravity is very weak in comparison to the electric force. Most objects have a net charge of zero, so the electric forces cancel out in most cases. This is not true with gravity; all objects with mass will have an attraction to all other masses.

37. Since both are conductors, by contact, or conduction, the two spheres will share the net charge of −2 C. Since they are the same size, each sphere will end up with −1 C.

38. . So if you double the diameter of the wire, the new resistance is one-fourth the original (R/4).

39. An ohmic resistor will have the same resistance even though the voltage and current are changing: . So, all you have to do is connect the resistor to different voltages, measure the current in each case, and calculate the resistance in each case to see if it is constant. Better yet, plot voltage versus current on a graph and make sure the graph is linear. If it is curved, the resistor is nonohmic.

40. . Here are your options for increasing the capacitance: (1) κ—insert an insulator between the plates with a higher dielectric constant; (2) A—increase the area of the plates; and (3) d—decrease the distance between the plates.

41. When the uncharged capacitor is first connected to the battery, it has no potential difference between the plates and offers no resistance to current. Thus, at first, the capacitor behaves like a wire. After a long time, the capacitor fills with opposite charges on the plates and builds a potential difference equal to, but in the opposite direction of, the battery. No more charge can move to the capacitor and it is “full.” Thus, in the end, the capacitor acts like a “disconnect” or “open switch” in the circuit and current flow stops.

42. The magnetic domains in a ferromagnetic material line up with the external B-Field amplifying the field. The magnetic field in a paramagnetic material also lines up with the external B-Field, but the effect is weak. Diamagnetic materials generate a magnetic field that is opposite to the external B-Field, partially cancelling the field. Superconductors exhibit diamagnetism and can completely cancel out the magnetic field inside themselves.

43. d is the distance between the slits in the case of a double slit interference pattern, or the width of the slit, in the case of a single slit interference pattern.

m is the “order” of the points of constructive or destructive interference. In the case of a double slit interference pattern, it represents the difference in path length from one source to a point on the screen, and the path length from the other source in terms of wavelengths.

θ is the angle between the central maximum “m” order maxima or minima.

λ is the wavelength of the wave traveling through the slits.

44. A double slit interference pattern has fairly evenly spaced maxima and minima in the interference pattern, while the single slit has a wide central maximum. If the distance between the double slits is the same as the width of the single slit, the maxima on the double slit will be minima for the single slit and vice versa. The wide central maximum of the single slit pattern will be twice as wide as that of the double slit pattern.

45. The interference pattern is created because light behaves as a wave. Light passing through each slit must travel a distance toward the screen. This distance can be measured in wavelengths. When the difference in distance from the slits to the screen is in whole multiples of a wavelength, the waves line up crest to crest to form constructive interference. When the travel distance from the two slits to the screen is off by a ½ wavelength, the waves strike the screen crest to trough for destructive interference.

46. Both exhibit wave behaviors: interference, diffraction, refraction, reflection, Doppler effect, etc. However, electromagnetic waves do not require a medium to travel. They are a self-propagating electric and magnetic wave. The energy of a mechanical wave is dictated by its amplitude. The energy of an EM wave depends on its frequency 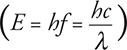. EM waves also exhibit the particle properties (photons).

47. Well, it depends. For clear substances, the remaining 20% of the light energy could have passed through and refracted. For opaque substances, the remaining 20% of the light energy is mostly absorbed. The key idea here is conservation of energy. Some light energy may reflect, some may transmit, and some may be absorbed, but it all adds up to the original 100% of the light energy.

48. When light enters a new medium, the wave fronts move at a new speed. This new speed causes the light to change direction. The only way light can travel into a new medium and not change direction is if it enters directly into the medium perpendicular to the surface, or if the speed of light in the new medium is the same as in the old medium.

49. (a) Light bends toward the normal when going from low to high index of refraction.

(b) Light bends away from the normal when going from high to low index of refraction.

(c) Total internal reflection can occur only when light goes from high to low index of refraction.

(d) sin θ_c = 1.3/1.5

50 For a convex (converging) lens:

• The incident ray parallel to the principal axis refracts through the far focal point.

• The incident ray through the near focal point refracts parallel to the principal axis.

• The incident ray through the center of the lens is unbent.

(Note that you don’t necessarily need to know this third ray for ray diagrams, but it’s legitimate.)

51. For a concave (diverging) lens:

• The incident ray parallel to the principal axis refracts as if it came from the near focal point.

• The incident ray toward the far focal point refracts parallel to the principal axis.

• The incident ray through the center of the lens is unbent.

(Note that you don’t necessarily need to know this third ray for ray diagrams, but it’s legitimate.)

52. One-eighth the original emission means it has gone through 3 half-lives (½ × ½ × ½ = ⅛) So the sample is 9 years old.

53. Photoelectric effect and photons

(a) If all you want is more electrons, just shine more green light, which will have more photons, on the surface.

(b) To get higher-energy electrons, you will need higher-energy light (photons) striking the surface. Use blue light, or UV light.

54. Conservation of charge, conservation of momentum, conservation of mass/energy (remember that mass and energy are two aspects of the same thing: E = mc²), conservation of nucleon number.

55. The photon has transferred energy and momentum from itself to the electron. The frequency decreases and the wavelength increases.

56. The electrons in the neon atom exhibit the wave properties of constructive and destructive interference. Thus, the elections can only exist in specific energy level locations. To jump up to the next energy level, the electron must absorb the specific amount of energy required to get there. It’s kind of like walking up steps. You need an exact amount of energy to climb from one step to the next. When electrons fall downward from one energy level to another, they must emit a photon of the exact energy difference between the levels: hence the bands of light.

57. The wave function of a particle is a probability distribution that tells us the likelihood of finding the particle at a specific location. The larger the positive or negative amplitude of the wave, at a specific location, the higher probability of finding the particle. If the amplitude is zero at a location, the particle will not be found at that location.

58. The mass of the uranium is larger than the combined mass of the thorium and alpha particle. The loss in mass is due to the kinetic energy gained by the alpha particle in the decay (E = mc²). Spontaneous nuclear reactions generate by-products that have less mass than the original.

59.

is used to find the wavelength of a photon only. You can remember this because of the c, meaning the speed of light—only the massless photon can move at the speed of light.

is the de Broglie wavelength of a massive particle. You can remember this because of the m—a photon has no mass, so this equation can never be used for a photon.

60. Gamma decay doesn’t affect the atomic mass or atomic number. In gamma decay, a photon is emitted from the nucleus, but because the photon carries neither charge nor an atomic mass unit, the number of protons and neutrons remains the same.

What Do I Know, and What Don’t I Know?

I’ll bet you didn’t get every question on all of the fundamentals quizzes correct. That’s okay. The whole point of these quizzes is for you to determine where to focus your study.

It’s a common mistake to “study” by doing 20 problems on a topic with which you are already comfortable. But that’s not studying . . . that’s a waste of time. You don’t need to drill yourself on topics you already understand! It’s also probably a mistake to attack what for you is the toughest concept in physics right before the exam. Virtually every student has that one chapter they just don’t get, however hard they try. That’s okay.

The fundamentals quizzes that you just took can tell you exactly what you should and should not study. Did you give correct answers with full confidence in the correctness of your response? In that case, you’re done with that topic. No more work is necessary. The place to focus your efforts is on the topics where either you gave wrong answers that you thought were right, or right answers that you weren’t really sure about.

Now that you have a decent idea of your content knowledge, it’s time to take a look at what the AP Physics 2 questions will be like. Turn the page to begin working on your AP question skills.