AP Physics C Exam

Part IV

Content Review for the AP Physics C Exam

Chapter 9 Laws of Gravitation

KEPLER’S LAWS

Johannes Kepler spent years of exhaustive study distilling volumes of data collected by his mentor, Tycho Brahe, into three simple laws that describe the motion of planets.

Kepler’s First Law

Every planet moves in an elliptical orbit, with the Sun at one focus.

Kepler’s Second Law

As a planet moves in its orbit, a line drawn from the Sun to the planet sweeps out equal areas in equal time intervals.

Kepler’s Third Law

If T is the period and a is the length of the semimajor axis of a planet’s orbit, then the ratio T²/a³ is the same for all planets orbiting the same star.

NEWTON’S LAW OF GRAVITATION

Newton eventually proved that Kepler’s first two laws imply a law of gravitation: Any two objects in the universe exert an attractive force on each other—called the gravitational force—whose strength is proportional to the product of the objects’ masses and inversely proportional to the square of the center-to-center distance between them. If we let G be the universal gravitational constant, then the strength of the gravitational force is given by the equation:

Consider a mass, m₁, close to the surface of Earth. We will use Newton’s Law of Gravitation and Newton’s Second Law to show that the gravitational acceleration of m₁ is independent of the mass of the object, as shown below.

The forces F_1-on-2 and F_2-on-1 act along the line that joins the bodies and form an action/reaction pair.

The first reasonably accurate numerical value for G was determined by Cavendish more than one hundred years after Newton’s Law was published. To three decimal places, the currently accepted value of G is

G = 6.67 × 10^–11 N • m²/kg²

Kepler’s Third Law then follows from Newton’s Law of Gravitation. We’ll show how this works, for the case of a circular orbit of radius R (which can be considered an elliptical orbit with eccentricity zero). If the orbit is circular, then Kepler’s Second Law says that the planet’s orbit speed, v, must be constant. Therefore, the planet executes uniform circular motion, and centripetal force is provided by the gravitational attraction of the Sun. If we let M be the mass of the Sun and m be the mass of the planet, then this last statement can be expressed mathematically as:

Note that this formula
makes sense when we
consider that each object
is contributing an
m/r term to the total
force of gravity.

The period of a planet’s orbit is the time it requires to make one revolution around the Sun, so dividing the distance covered, 2πR, by the planet’s orbit speed, v, we have

Equation (1) implies that v² = GM/R. Squaring both sides of Equation (2) and then substituting v² = GM/R, we find that

Therefore,

which is Kepler’s Third Law for a circular orbit of radius R.

Acceleration of Gravity Due to Large Bodies

We have been using the acceleration due to gravity g = 10 m/s² for all objects falling near the surface of Earth. We have assumed that the mass does not affect the acceleration of gravity and now we will show why.

Assume a small mass m is located near a large body (i.e., a planet or star) of mass M. The gravitational force on the object near the surface will equal the mass of the object times the acceleration of gravity a_g. The equation below shows how the mass of the object cancels out, and the acceleration of gravity is independent of that mass of the object.

From this expression we can see that the acceleration due to gravity for any object on a planet would be related to the mass and radius of the planet, but not the mass of the object.

THE GRAVITATIONAL ATTRACTION DUE TO AN EXTENDED BODY

Newton’s Law of Gravitation is really a statement about the force between two point particles: objects that are very small in comparison to the distance between them. Newton also proved that a uniform sphere attracts another body as if all of the sphere’s mass were concentrated at its center.

For this reason, we can apply Newton’s Law of Gravitation to extended bodies, that is, to objects that are not small relative to the distance between them.

Additionally, a uniform shell of mass does not exert a gravitational force on a particle inside it. This means that if a spherical planet is uniform, then as we descend into it, only the mass of the sphere underneath us exerts a gravitational force; the shell above exerts no force because we’re inside it.

Example 1 What is the gravitational force on a particle of mass m at a distance x from the center of a spherically symmetric planet of uniform density ρ, total mass M, and radius R for

(a) x ≥ R

(b) x < R

Solution.

(a) If x ≥ R, then the planet can be treated as a point particle with all its mass concentrated at its center, and

(b) However, if x < R, then only the mass within the sphere of radius x exerts a gravitational force on the particle. Since the volume of such a sphere is (4/3)πx³, its mass is (4/3)πx³ρ; we’ll denote this by M_within _x. Since the mass of the entire planet is (4/3)πR³ρ, we see that

Therefore, the force that this much mass exerts on the particle of mass m is

In summary then,

Example 2 Given that the radius of Earth is 6.37 × 10⁶ m, determine the mass of Earth.

Solution. Consider a small object of mass m near the surface of Earth (mass M). Its weight is mg, but its weight is just the gravitational force it feels due to Earth, which is GMm/R². Therefore,

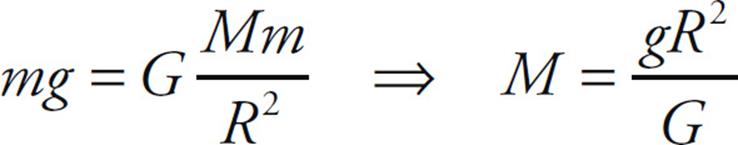
Since we know that g = 10 m/s² and G = 6.67 × 10^–11 N•m²/kg², we can substitute to find

Example 3 We can derive the expression GM/R² by equating mg and GMm/R² (as we did in the previous example), and this gives the magnitude of the absolute gravitational acceleration, a quantity that’s sometimes denoted g₀. The notation g is acceleration, but with the spinning of Earth taken into account. Show that if an object is at the equator, its measured weight (the weight that a scale would measure), mg, is less than its true weight, mg₀, and compute the weight difference for a person of mass m = 60 kg.

Solution. Imagine looking down at Earth from above the North Pole.

The net force toward the center of Earth is F₀ – F_N, which provides the centripetal force on the object. Therefore,

Since v = 2πR/T, where T is Earth’s rotation period we have

or, since F₀ = mg₀ and F_N = mg,

Since the quantity 4p²mR/T² is positive, mg must be less than mg₀. The difference between mg₀ and mg, for a person of mass m = 60 kg, is only:

and the difference between g₀ and g is

Example 4 Communications satellites are often parked in geosynchronous orbits above Earth’s surface. Such satellites have orbit periods that are equal to Earth’s rotation period, so they remain above the same position on Earth’s surface. Determine the altitude and the speed that a satellite must have to be in a geosynchronous orbit above a fixed point on Earth’s equator. (The mass of Earth is 5.98 × 10²⁴ kg.)

Solution. Let m be the mass of the satellite, M be the mass of Earth, and R be the distance from the center of Earth to the position of the satellite. The gravitational pull of Earth provides the centripetal force on the satellite, so

The orbit speed of the satellite is 2πR/T, so

which implies that

Now, the key feature of a geosynchronous orbit is that its period matches Earth’s rotation period, T = 24 hr. Substituting the numerical values of G, M, and T into this expression, we find that

Therefore, if r_E is the radius of Earth, then the satellite’s altitude above Earth’s surface must be

h = R – r_E = (4.23 × 10⁷ m) – (6.37 × 10⁶ m) = 3.59 × 10⁷ m

which is equal to 5.6r_E. The speed of the satellite in this orbit is, from the first equation in our calculations,

regardless of the mass of the satellite (well, as long as m < < M).

Example 5 A uniform, slender bar of mass M has length L. Determine the gravitational force it exerts on the point particle of mass m shown below:

Solution. Since the bar is an extended body (and not spherically symmetric), we must calculate F using an integral. Select an arbitrary segment of length dx and mass dM in the bar, at a distance x from its left-hand end.

Then, since the bar is uniform, dM = (M/L)dx, so the gravitational force between m and dM is

Now, by adding (that is, by integrating) all of the contributions dF, we get the total gravitational force, F:

GRAVITATIONAL POTENTIAL ENERGY

When we developed the equation U = mgh for the gravitational potential energy of an object of mass m at height h above the surface of Earth, we took the surface of Earth to be our U = 0 reference level and assumed that the height, h, was small compared to Earth’s radius. In that case, the variation in g was negligible, so g was treated as constant. The work done by gravity as an object was raised to height h was then simply –F_grav × s = –mgh, so U_grav, which by definition equals –W_{by grav}, was mgh.

But now we’ll take variations in g into account and develop a general equation for gravitational potential energy, one that isn’t restricted to small altitude changes.

Consider an object of mass m at a distance r₁ from the center of Earth (or any spherical body) moving by some means to a position r₂:

How much work did the gravitational force perform during this displacement? The answer is given by the equation:

Therefore, since U_grav = –W_{by grav}, we get

Let’s choose our U = 0 reference at infinity. That is, we decide to allow U₂ → 0 as r₂ → ∞. Then this equation becomes

Notice that, according to this equation (and our choice of U = 0 when r = ∞), the gravitational potential energy is always negative. This just means that energy has to be added to bring an object (mass m) bound to the gravitational field of M to a point very far from M, at which U = 0.

A PROOF OF EQUATION (*)

Because the gravitational force is not constant over the displacement, the work done by this force must be calculated using a definite integral:

Displacement can be broken into a series of infinitesimal steps of two types: Those that are at a constant distance from Earth’s center and those that are along a radial line going away from Earth’s center. The result is that the displacement is equivalent to the sum of two curves C₁ + C₂:

The gravitational force along C₁ does no work, because it’s always perpendicular to the displacement. Along C₂, the inward gravitational force is in the opposite direction from the outward displacement, so along this ray,

Therefore,

Example 6 With what minimum speed must an object of mass m be launched in order to escape Earth’s gravitational field? (This is called escape speed, v_esc.)

Solution. When launched, the object is at the surface of Earth (r_i = r_E) and has an upward, initial velocity of magnitude v_i. To get it far away from Earth, we want to bring its gravitational potential energy to zero, but to find the minimum launch speed, we want the object’s final speed to be zero by the time it gets to this distant location. So, by Conservation of Energy,

Note: This is the minimum
speed needed to escape
Earth’s gravitational field
but, in this situation, a
projectile would also have
to contend with the Sun’s
gravitational field.

which gives

Substituting the known numerical values for G, M_E, and r_E gives us:

Example 7 A satellite of mass m is in a circular orbit of radius R around Earth (radius r_E, mass M).

(a) What is its total mechanical energy (where U_grav is considered zero as R approaches infinity)?

(b) How much work would be required to move the satellite into a new orbit, with radius 2R?

Solution.

(a) The mechanical energy, E, is the sum of the kinetic energy, K, and potential energy, U. You can calculate the kinetic energy since you know that the centripetal force on the satellite is provided by the gravitational attraction of Earth:

Therefore,

(b) From the equation K_i + U_i + W = K_f + U_f, we see that

W = (K_f + U_f) − (K_i + U_i)
= E_f − E_i

Therefore, the amount of work necessary to effect the change in the satellite’s orbit radius from R to 2R is

A Note on Elliptical Orbits

The expression for the total energy of a satellite in a circular orbit of radius R [derived in Example 7(a)] is:

And this also holds for a satellite traveling in an elliptical orbit, if the radius R is replaced by a, (the length of the semimajor axis):

Example 8 An asteroid of mass m is in an elliptical orbit around the Sun (mass M). Assume that m << M.

(a) What is the total energy of the asteroid?

(b) What is the ratio of v₁ (the asteroid’s speed at aphelion) to v₂ (the asteroid’s speed at perihelion)? Write your answer in terms of r₁ and r₂.

Solution.

(a) The total energy of the asteroid is equal to –GMm/2a, where a is the semimajor axis. However, notice in the figure above that 2a = r₁ + r₂. Therefore, the total energy of the asteroid is

(b) One way to answer this question is to invoke Conservation of Angular Momentum. When the asteroid is at aphelion, its angular momentum (with respect to the center of the Sun) is L₁ = r₁mv₁. When the asteroid is at perihelion, its angular momentum is L₂ = r₂mv₂. Therefore,

This tells us that the asteroid’s speed at aphelion is less than its speed at perihelion (because r₂/r₁ < 1), as implied by Kepler’s Second Law (a line drawn from the Sun to the asteroid must sweep out equal areas in equal time intervals). The closer the asteroid is to the Sun, the faster it has to travel to make this true.

(c) As you know, the time necessary for the asteroid to make a complete orbit around the Sun is the orbit period, T. Using Kepler’s Third Law, with a = (r₁ + r₂), we find

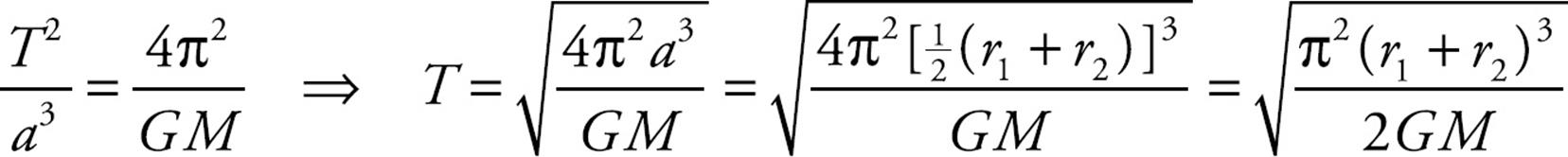
ORBITS OF THE PLANETS

Kepler’s First Law states that the planets’ orbits are ellipses, but the ellipses that the planets in our solar system travel are nearly circular. The deviation of an ellipse from a perfect circle is measured by a parameter called its eccentricity. The eccentricity, e, is the ratio of c (the distance between the center and either focus) to a, the length of the semimajor axis. For every point on the ellipse, the sum of the distances to the foci (plural of focus) is a constant (and is equal to 2a in the figure below).

Kepler’s First Law also states that one of the foci of a planet’s elliptical orbit is located at the position of the Sun. Actually, the focus is at the center of mass of the Sun-planet system, because when one body orbits another, both bodies orbit around their center of mass, a point called thebarycenter.

For most of the planets, which are much less massive than the Sun, this correction to Kepler’s First Law has little significance, because the center of mass of the Sun and the planet system is close enough to the Sun’s center. For example, let’s figure out the center of mass of the Sun-Earth system. The mass of Earth is m = 5.98 × 10²⁴ kg, the mass of the Sun is M = 1.99 × 10³⁰ kg, and the Sun-Earth distance averages R = 1.496 × 10¹¹ m. Therefore, letting x = 0 be at the Sun’s center, we have

So the center of mass of the Sun-Earth system is only 450 km from the center of the Sun, a distance of less than 0.1% of the Sun’s radius.

Example 9 Derive a corrected version of Kepler’s Third Law for the following orbiting system. Both bodies have orbit period T.

Solution. The centripetal force on each body is provided by the gravitational pull of the other body, so

which imply

But, since both bodies have the same orbit period, T, we have

Substituting these results into the preceding pair of equations gives us:

which simplify to

Adding this last pair of equations gives us the desired result:

Note that this final equation is a general version of Kepler’s Third Law for a circular orbit derived earlier, T²/R³ = 4π²/GM, where it was assumed that the planet orbited at a distance R from the center of the Sun.

Example 10 An artificial satellite of mass m travels at a constant speed in a circular orbit of radius R around Earth (mass M). What is the speed of the satellite?

Solution. The centripetal force on the satellite is provided by Earth’s gravitational pull. Therefore,

Solving this equation for v yields

Notice that the satellite’s speed doesn’t depend on its mass; even if it were a baseball, if its orbit radius were R, then its orbit speed would still be .

CHAPTER 9 REVIEW QUESTIONS

The answers and explanations can be found in Chapter 16.

Section I: Multiple Choice

1. If the distance between two point particles is doubled, then the gravitational force between them

(A) decreases by a factor of 4

(B) decreases by a factor of 2

(D) increases by a factor of 4

(E) cannot be determined without knowing the masses

2. At the surface of Earth, an object of mass m has weight w. If this object is transported to a height above the surface that’s twice the radius of Earth, then, at the new location,

(A) its mass is m/2 and its weight is w/2

(B) its mass is m and its weight is w/2

(D) its mass is m and its weight is w/4

(E) its mass is m and its weight is w/9

3. A moon of mass m orbits a planet of mass 100m. Let the strength of the gravitational force exerted by the planet on the moon be denoted by F₁, and let the strength of the gravitational force exerted by the moon on the planet be F₂. Which of the following is true?

(A) F₁ = 100F₂

(B) F₁ = 10F₂

(D) F₂ = 10F₁

(E) F₂ = 100F₁

4. The dwarf planet Pluto has 1/500 the mass and 1/15 the radius of Earth. What is the value of g (in m/s²) on the surface of Pluto?

(A)

(B)

(C)

(D)

(E)

5. A satellite is currently orbiting Earth in a circular orbit of radius R; its kinetic energy is K₁. If the satellite is moved and enters a new circular orbit of radius 2R, what will be its kinetic energy?

(A) K₁/4

(B) K₁/2

(D) 2K₁

(E) 4K₁

6. A moon of Jupiter has a nearly circular orbit of radius R and an orbit period of T. Which of the following expressions gives the mass of Jupiter?

(A) 2πR/T

(B) 4π²R/T²

(D) 4πR²/(GT²)

(E) 4π²R³/(GT²)

7. Two large bodies, Body A of mass m and Body B of mass 4m, are separated by a distance R. At what distance from Body A, along the line joining the bodies, would the gravitational force on an object be equal to zero? (Ignore the presence of any other bodies.)

(A) R/16

(B) R/8

(D) R/4

(E) R/3

8. The mean distance from Saturn to the Sun is 9 times greater than the mean distance from Earth to the Sun. How long is a Saturn year?

(A) 18 Earth years

(B) 27 Earth years

(D) 243 Earth years

(E) 729 Earth years

9. The Moon has mass M and radius R. A small object is dropped from a distance of 3R from the Moon’s center. The object’s impact speed when it strikes the surface of the Moon is equal to for k =

(A) 1/3

(B) 2/3

(D) 4/3

(E) 3/2

10. Two satellites, A and B, orbit a planet in circular orbits having radii R_A and R_B, respectively, as shown above. If R_B = 3R_A, the velocities v_A and v_B of the two satellites are related by which of the following?

(A) v_B = v_A

(B) v_B = 3v_A

(D) v_B = v_A

(E) v_B =

Section II: Free Response

1. Consider two uniform spherical bodies in deep space. Sphere 1 has mass m₁ and Sphere 2 has mass m₂. Starting from rest from a distance R apart, they are gravitationally attracted to each other.

(a) Compute the acceleration of Sphere 1 when the spheres are a distance R/2 apart.

(b) Compute the acceleration of Sphere 2 when the spheres are a distance R/2 apart.

(d) Compute the speed of Sphere 2 when the spheres are a distance R/2 apart.

Now assume that these spheres orbit their center of mass with the same orbit period, T.

(e) Determine the radii of their orbits. Write your answer in terms of m₁, m₂, T, and fundamental constants.

2. A satellite of mass m is in the elliptical orbit shown below around Earth (radius r_E, mass M). Assume that m << M.

(a) Determine v₁, the speed of the satellite at perigee (the point of the orbit closest to Earth). Write your answer in terms of r₁, r₂, M, and G.

(b) Determine v₂, the speed of the satellite at apogee (the point of the orbit farthest from Earth). Write your answer in terms of r₁, r₂, M, and G.

(d) What is the satellite’s angular momentum (with respect to Earth’s center) when it’s at apogee?

(e) Determine the speed of the satellite when it’s at the point marked X in the figure.

(f) Determine the period of the satellite’s orbit. Write your answer in terms of r₁, r₂, M, and fundamental constants.

Summary

Newton’s Law of Gravitation

Newton’s Law of Gravitation gives the force between any two point masses, regardless of their mass or location. This uniform circular motion can also be described by an angular velocity and a centripetal acceleration.

Circular Orbits

General Orbits

The gravitational potential energy is represented by the following formula:

Both mechanical energy and angular momentum are conserved for orbits.

E_total = 0

Systems are bound when the total mechanical energy is less than zero. This means that the gravitational potential energy is greater than the kinetic energy of the system.

For an object to escape, its kinetic energy must be greater than or equal to its gravitational potential energy.

for M₁ to escape the pull of M₂.

Gravity of Spheres and Shells

The gravity due to a spherical shell of mass, M, and radius, R, where the mass is at a distance, r, away from the center of the shell is represented by the equations below.

Outside the shell is

and the gravity inside the shell is F_g = 0

The gravity due to a uniform, solid sphere where a small mass, m, is at a distance, r, away from the center of the sphere is represented by the equations below.

Outside the sphere is

and the gravity inside the shell is

The gravity of a spherically symmetric sphere of mass, M, and radius, R (that is, ρ(r)), is represented by the equation