Linear Momentum - AP Physics B Exam

AP Physics B Exam

5 Linear Momentum

INTRODUCTION

When Newton first expressed his Second Law, he didn”t write F_net = ma. Instead, he expressed the law in the words, The alteration of motion is … proportional to the … force impressed.… By “motion,” he meant the product of mass and velocity, a vector quantity known as linear momentum and denoted by p:

p = mv

So Newton”s original formulation of the Second Law read ∆p ∝ F, or, equivalently, F ∝ ∆p. But a large force that acts for a short period of time can produce the same change in linear momentum as a small force acting for a greater period of time. Knowing this, we can turn the proportion above into an equation, if we take the average force that acts over the time interval ∆t:

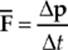
This equation becomes F = ma, since ∆p/∆t = ∆(mv)/∆t = m (∆v/∆t) = ma (assuming that m remains constant).

Example 5.1 A golfer strikes a golf ball of mass 0.05 kg, and the time of impact between the golf club and the ball is 1 ms. If the ball acquires a velocity of magnitude 70 m/s, calculate the average force exerted on the ball.

Solution. Using Newton”s Second Law, we find

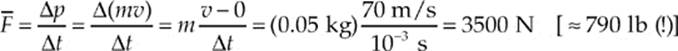
IMPULSE

The product of force and the time during which it acts is known as impulse; it”s a vector quantity that”s denoted by J:

In terms of impulse, Newton”s Second Law can be written in yet another form:

J = ∆p

Sometimes this is referred to as the impulse–momentum theorem, but it”s just another way of writing Newton”s Second Law. The impulse delivered to an object may be found by taking the area under a force-vs.-time graph. In physics, “the area under a graph,” really means the area between the line and the horizontal axis.

You might notice some similarities between impulse causing a change in momentum (J = ∆p) and work causing a change in kinetic energy (W = ∆K). Impulse talks about pushing or pulling for some amount of time and work deals with pushing or pulling for some displacement. Both can change the motion of an object. As a matter of fact, many times when you exert a force on an object, you change both the kinetic energy and the momentum of the object. Momentum and energy are both conserved. However, these two concepts are quite different. Whereas work can go into different forms of energy (heat, potential energy, etc.), impulse has one and only one place to go—momentum. Finally, energy is a scalar and has no direction whereas momentum is a vector and must follow all the rules of vectors as covered in Chapter 1.

Example 5.2 A football team”s kicker punts the ball (mass = 0.4 kg) and gives it a launch speed of 30 m/s. Find the impulse delivered to the football by the kicker”s foot and the average force exerted by the kicker on the ball, given that the impact time is 8 ms.

Solution. Impulse is equal to change in linear momentum, so

J = ∆p = p_f – p_i = p_f = mv = (0.4 kg)(30 m/s) = 12 kg·m/s

Using the equation = J/Δt, we find that the average force exerted by the kicker is

Example 5.3 An 80 kg stuntman jumps out of a window that”s 45 m above the ground.

(a) How fast is he falling when he reaches ground level?

(b) He lands on a large, air-filled target, coming to rest in 1.5 s. What average force does he feel while coming to rest?

Solution.

(a) His gravitational potential energy turns into kinetic energy: mgh= mv², so

(You could also have answered this question using Big Five #5.)

(b) Using = Δp/Δt, we find that

The negative signs in the vector answers to (b) and (c) simply tell you that the forces are acting in the opposite direction of motion and will cause the object to slow down. This force is equivalent to about 27 tons (!), more than enough to break bones and cause fatal brain damage. Notice how crucial impact time is: Increasing the slowing-down time reduces the acceleration and the force, ideally enough to prevent injury. This is the purpose of air bags in cars, for instance.

Example 5.4 A small block of mass m = 0.07 kg, initially at rest, is struck by an impulsive force F of duration 10 ms whose strength varies with time according to the following graph:

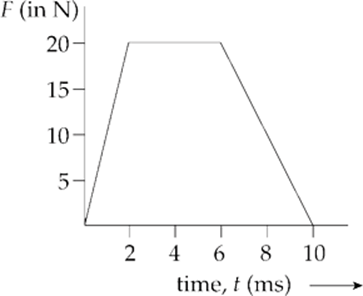
What is the resulting speed of the block?

Solution. The impulse delivered to the block is equal to the area under the F-vs.-t graph. The region is a trapezoid, so its area, (base₁ + base₂) × height, can be calculated as follows:

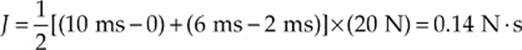
Now, by the impulse–momentum theorem,

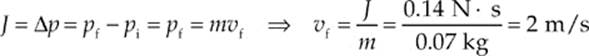
CONSERVATION OF LINEAR MOMENTUM

Newton”s Third Law says that when one object exerts a force on a second object, the second object exerts an equal but opposite force on the first. Since Newton”s Second Law says that the impulse delivered to an object is equal to the resulting change in its linear momentum, J = ∆p, the two interacting objects experience equal but opposite momentum changes (assuming that we have an isolated system in which there are no external forces), which implies that the total linear momentum of the system remains constant. In fact, given any number of interacting objects, each pair that comes in contact will undergo equal but opposite momentum changes, so the result described for two interacting objects will actually hold for any number of objects, given that the only forces they feel are from each other. This means that, in an isolated system, the total linear momentum will remain constant. This is the Law of Conservation of Linear Momentum.

Example 5.5 An astronaut is floating in space near her shuttle when she realizes that the cord that”s supposed to attach her to the ship has become disconnected. Her total mass (body + suit + equipment) is 91 kg. She reaches into her pocket, finds a 1 kg metal tool, and throws it out into space with a velocity of 9 m/s directly away from the ship. If the ship is 10 m away, how long will it take her to reach it?

Solution. Here, the astronaut + tool are the system. Because of Conservation of Linear Momentum,

Using distance = rate × time, we find

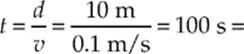
COLLISIONS

Conservation of Linear Momentum is routinely used to analyze collisions. The objects whose collision we will analyze form the system, and although the objects exert forces on each other during the impact, these forces are only internal (they occur within the system), and the system”s total linear momentum is conserved.

Collisions are classified into two major categories: (1) elastic and (2) inelastic. A collision is said to be elastic if kinetic energy is conserved. Ordinary macroscopic collisions are never truly elastic, because there is always a change in energy due to energy transferred as heat, deformation of the objects, and the sound of the impact. However, if the objects do not deform very much (for example, two billiard balls or a hard glass marble bouncing off a steel plate), then the loss of initial kinetic energy is small enough to be ignored, and the collision can be treated as virtually elastic. Inelastic collisions, then, are ones in which the total kinetic energy is different after the collision. An extreme example of inelasticism is completely (or perfectly or totally) inelastic. In this case, the objects stick together after the collision and move as one afterward. In all cases of isolated collisions (elastic or not), Conservation of Linear Momentum states that

total p_{before collision} = total p_{after colision}

Example 5.6 Two balls roll toward each other. The red ball has a mass of 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.2 kg and a speed of 2 m/s. After the head-on collision, the red ball continues forward with a speed of 2 m/s. Find the speed of the green ball after the collision. Was the collision elastic?

Solution. First remember that momentum is a vector quantity, so the direction of the velocity is crucial. Since the balls roll toward each other, one ball has a positive velocity while the other has a negative velocity. Let”s call the red ball”s velocity before the collision positive; then v_red = +4 m/s, and v_green = –2 m/s. Using a prime to denote after the collision, Conservation of Linear Momentum gives us the following:

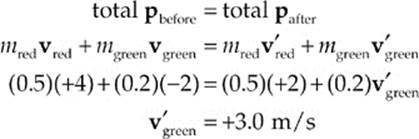
Notice that the green ball”s velocity was reversed as a result of the collision; this typically happens when a lighter object collides with a heavier object. To see whether the collision was elastic, we need to compare the total kinetic energies before and after the collision.

Initially

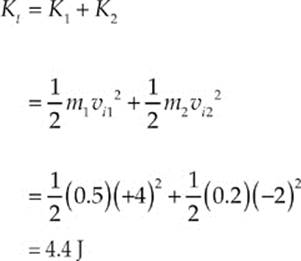
There are 4.4 joules at the beginning. At the end

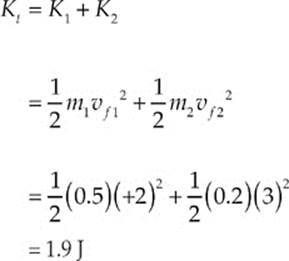
So, there is less kinetic energy at the end compared to the beginning. Kinetic energy was lost (so the collision was inelastic); this is usually the case with macroscopic collisions. Most of the lost energy was transferred as heat; the two objects are both slightly warmer as a result of the collision.

Example 5.7 Two balls roll toward each other. The red ball has a mass of 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2 m/s. If the collision is completely inelastic, determine the velocity of the composite object after the collision.

Solution. If the collision is completely inelastic, then, by definition, the masses stick together after impact, moving with a velocity, v′. Applying Conservation of Linear Momentum, we find

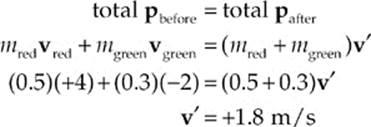
Example 5.8 A 500 kg car travels 20 m/s due north. It hits a 500 kg car traveling due west at 30 m/s. The cars lock bumpers and stick together. What is the velocity the instant after impact?

Solution. This problem illustrates the vector nature of numbers. First, look only at the x (east-west) direction. There is only one car moving west and its momentum is given by:

p = mv ⇒ (500kg)(30m/s) = 15,000 kg · m/s west

Next, look only at the y (north-south) direction. There is only one car moving north and its momentum is given by:

p = mv ⇒ (500kg)(20m/s) = 10,000 kg · m/s north

The total final momentum is the resultant of these two vectors. Use Pythagorean theorem:

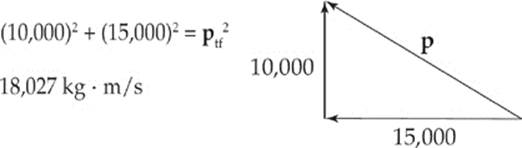
To find the total velocity you need to solve for v using

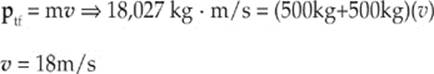
However, we are not done yet because velocity has both a magnitude (which we now know is 12 m/s) and a direction. The direction can be expressed using tanθ = 10,000/15,000 so θ = tan^–1 (10,000/15,000) or 33.7 degrees north of west. Again, most of the Physics B test is in degrees, not radians.

Example 5.9 An object of mass m moves with velocity v toward a stationary object of mass 2m. After impact, the objects move off in the directions shown in the following diagram:

(a) Determine the magnitudes of the velocities after the collision (in terms of v).

(b) Is the collision elastic? Explain your answer.

Solution.

(a) Conservation of Linear Momentum is a principle that establishes the equality of two vectors: p_total before the collision and p_total after the collision. Writing this single vector equation as two equations, one for the x component and one for the y, we have

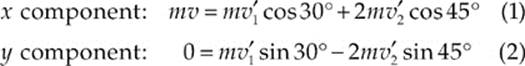
Adding these equations eliminates v′₂, because cos 45° = sin 45°.

mv = mv′₁(cos 30° + cos 30°)

and lets us determine v′₁:

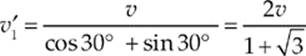
Substituting this result into Equation (2) gives us

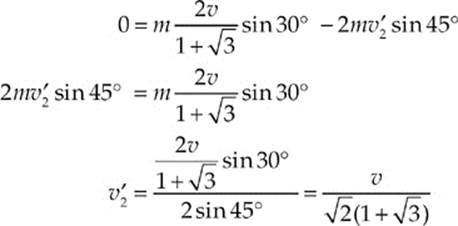
(b) The collision is elastic only if kinetic energy is conserved. The total kinetic energy after the collision, K′, is calculated as follows:

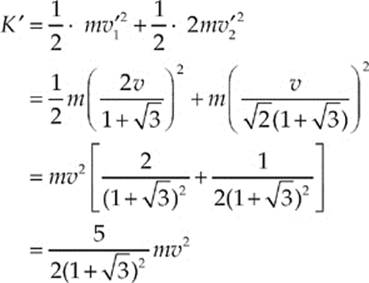
However, the kinetic energy before the collision is just K = mv², so the fact that

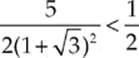
tells us that K′ is less than K, so some kinetic energy is lost; the collision is inelastic.

CHAPTER 5 REVIEW QUESTIONS

Solutions can be found in Chapter 18.

SECTION I: MULTIPLE CHOICE

1. An object of mass 2 kg has a linear momentum of magnitude 6 kg · m/s. What is this object”s kinetic energy?

(A) 3 J

(B) 6 J

(D) 12 J

(E) 18 J

2. A ball of mass 0.5 kg, initially at rest, acquires a speed of 4 m/s immediately after being kicked by a force of strength 20 N. For how long did this force act on the ball?

(A) 0.01 s

(B) 0.02 s

(D) 0.2 s

(E) 1 s

3. A box with a mass of 2 kg accelerates in a straight line from 4 m/s to 8 m/s due to the application of a force whose duration is 0.5 s. Find the average strength of this force.

(A) 2 N

(B) 4 N

(D) 12 N

(E) 16 N

4. A ball of mass m traveling horizontally with velocity v strikes a massive vertical wall and rebounds back along its original direction with no change in speed. What is the magnitude of the impulse delivered by the wall to the ball?

(A) 0

(B) mv

(D) 2mv

(E) 4mv

5. Two objects, one of mass 3 kg and moving with a speed of 2 m/s and the other of mass 5 kg and speed 2 m/s, move toward each other and collide head-on. If the collision is perfectly inelastic, find the speed of the objects after the collision.

(A) 0.25 m/s

(B) 0.5 m/s

(D) 1 m/s

(E) 2 m/s

6. Object 1 moves toward Object 2, whose mass is twice that of Object 1 and which is initially at rest. After their impact, the objects lock together and move with what fraction of Object 1”s initial kinetic energy?

(A) 1/18

(B) 1/9

(D) 1/3

(E) None of the above

7. Two objects move toward each other, collide, and separate. If there was no net external force acting on the objects, but some kinetic energy was lost, then

(A) the collision was elastic and total linear momentum was conserved

(B) the collision was elastic and total linear momentum was not conserved

(D) the collision was not elastic and total linear momentum was not conserved

(E) None of the above

8. Two frictionless carts (mass = 500g each) are sitting at rest on a perfectly level table. Teacher taps the release so that one cart pushes off the other. If one of the carts has a speed of 2 m/s, then what is the final momentum of the system (in kg · m/s)?

(A) Not enough information

(B) 2000

(D) 2

(E) 0

9. A wooden block of mass M is moving at speed V in a straight line.

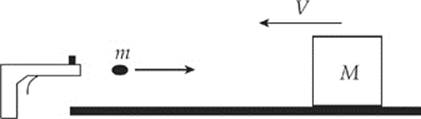
How fast would the bullet of mass m need to travel to stop the block (assuming that the bullet became embedded inside)?

(A) mV/(m + M)

(B) MV/(m + M)

(D) MV/m

(E) (m + M)V/m

10. Which of the following best describes a perfectly inelastic collision free of external forces?

(A) Total linear momentum is never conserved.

(B) Total linear momentum is sometimes conserved.

(D) Kinetic energy is sometimes conserved.

(E) Kinetic energy is always conserved.

SECTION II: FREE RESPONSE

1. A steel ball of mass m is fastened to a light cord of length L and released when the cord is horizontal. At the bottom of its path, the ball strikes a hard plastic block of mass M = 4m, initially at rest on a frictionless surface. The collision is elastic.

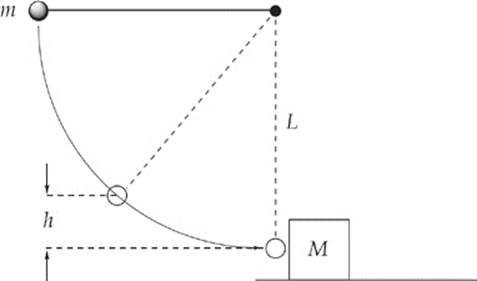
(a) Find the tension in the cord when the ball”s height above its lowest position is L. Write your answer in terms of m and g.

(b) Find the speed of the block immediately after the collision.

2. A ballistic pendulum is a device that may be used to measure the muzzle speed of a bullet. It is composed of a wooden block suspended from a horizontal support by cords attached at each end. A bullet is shot into the block, and as a result of the perfectly inelastic impact, the block swings upward. Consider a bullet (mass m) with velocity v as it enters the block (mass M). The length of the cords supporting the block each have length L. The maximum height to which the block swings upward after impact is denoted by y, and the maximum horizontal displacement is denoted by x.

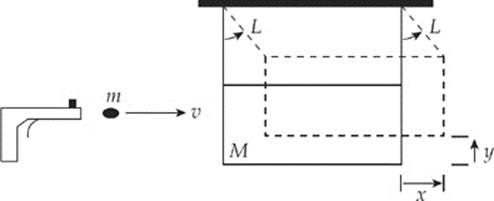
(a) In terms of m, M, g, and y, determine the speed v of the bullet.

(b) What fraction of the bullet”s original kinetic energy is lost as a result of the collision? What happens to the lost kinetic energy?

(d) Once the block begins to swing, does the momentum of the block remain constant? Why or why not?

SUMMARY

· Momentum is a vector quantity given by p = mv. If you push on an object for some amount of time we call that an impulse (J). Impulses cause a change in momentum. Impulse is also a vector quantity and these ideas are summed up in the equations J = Δt or J = Δp.

· Momentum is a conserved quantity in a closed system (that is, a system with no external forces). That means:

total p_i = total p_f.

· Overall strategy for conservation of momentum problems:

1. Create a coordinate system.

2. Break down each object”s momentum into x and y components. That is p_x = p cos θ and p_y = p sin θ for any given object.

3. and

4. Sometimes you end up rebuilding vectors in the end.

Remember total p = and the angle is given by θ = tan⁻¹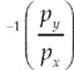.