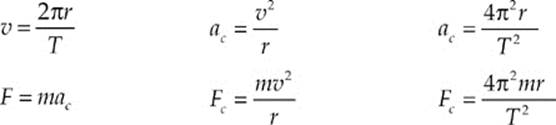Uniform Circular Motion and Newton's Law of Gravitation

AP Physics B Exam

6 Uniform Circular Motion and Newton”s Law of Gravitation

INTRODUCTION

In Chapter 2, we considered two types of motion: straight-line motion and parabolic motion. We will now look at motion that follows a circular path, such as a rock on the end of a string, a horse on a merry-go-round, and (to a good approximation) the Moon around Earth and Earth around the Sun.

UNIFORM CIRCULAR MOTION

Let”s simplify matters and consider the object”s speed around its path to be constant. This is called uniform circular motion. You should remember that although the speed may be constant, the velocity is not, because the direction of the velocity is always changing. Since the velocity is changing, there must be acceleration. This acceleration does not change the speed of the object; it only changes the direction of the velocity to keep the object on its circular path. Also, in order to produce an acceleration, there must be a force; otherwise, the object would move off in a straight line (Newton”s First Law).

The figure on the left on the next page shows an object moving along a circular trajectory, along with its velocity vectors at two nearby points. The vector v₁ is the object”s velocity at time t = t₁, and v₂ is the object”s velocity vector a short time later (at time t = t₂). The velocity vector is always tangential to the object”s path (whatever the shape of the trajectory). Notice that since we are assuming constant speed, the lengths of v₁ and v₂ (their magnitudes) are the same.

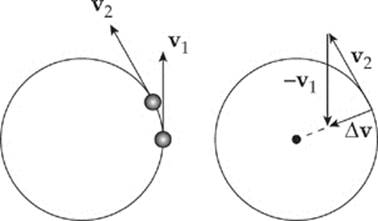
Since ∆v = v₂ – v₁ points toward the center of the circle (see the figure on the right), so does the acceleration, since a = ∆v/∆t. Because the acceleration vector points toward the center of the circle, it”s called centripetal acceleration, or a_c. The centripetal acceleration is what turns the velocity vector to keep the object traveling in a circle. The magnitude of the centripetal acceleration depends on the object”s speed, v, and the radius, r, of the circular path according to the equation

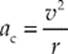
Example 6.1 An object of mass 5 kg moves at a constant speed of 6 m/s in a circular path of radius 2 m. Find the object”s acceleration and the net force responsible for its motion.

Solution. By definition, an object moving at constant speed in a circular path is undergoing uniform circular motion. Therefore, it experiences a centripetal acceleration of magnitude v²/r, always directed toward the center of the circle:

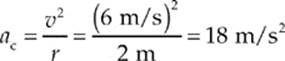
The force that produces the centripetal acceleration is given by Newton”s Second Law, coupled with the equation for centripetal acceleration:

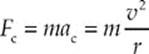
This equation gives the magnitude of the force. As for the direction, recall that because F = ma, the directions of F and a are always the same. Since centripetal acceleration points toward the center of the circular path, so does the force that produces it. Therefore, it”s called centripetal force. The centripetal force acting on this object has a magnitude of F_c = ma_c = (5 kg)(18 m/s²) = 90 N.

Example 6.2 A 10.0 kg mass is attached to a string that has a breaking strength of 200 N. If the mass is whirled in a horizontal circle of radius 80 cm, what maximum speed can it have?

Solution. The first thing to do in problems like this is to identify what force(s) provide the centripetal acceleration. Notice that this is a horizontal circle. We can limit our examination to the horizontal (x) direction. Because gravity exerts a force in the y direction, it can be ignored. If we were given a problem with a vertical circle, we would have to include the effects of gravity, as demonstrated in Example 6.4. In this example, the tension in the string provides the centripetal force:

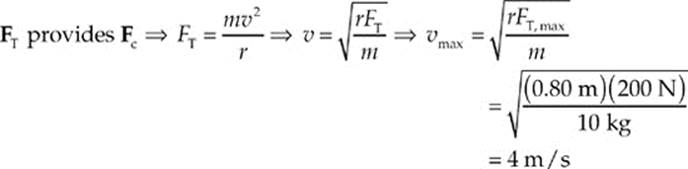
Notice the unit change from 80 cm to 0.80 m. As a general rule, stick to kg, m, and s because the Newton is composed of these units.

Example 6.3 An athlete who weighs 800 N is running around a curve at a speed of 5.0 m/s in an arc whose radius of curvature, r, is 5.0 m. Find the centripetal force acting on him. What provides the centripetal force? What could happen to him if r were smaller?

Solution. Using the equation for the strength of the centripetal force, we find that

In this case, static friction provides the centripetal force. Since the coefficient of static friction between his shoes and the ground is most likely around 1, the maximum force that static friction can exert is μ_sF_N ≈ F_N = F_w = 800 N. Fortunately, 800 N is greater than 400 N. But notice that if the radius of curvature of the arc were much smaller, then F_c would become greater than what static friction could handle, and he would slip.

Example 6.4 A roller-coaster car enters the circular-loop portion of the ride. At the very top of the circle (where the people in the car are upside down), the speed of the car is 15 m/s, and the acceleration points straight down. If the diameter of the loop is 40 m and the total mass of the car (plus passengers) is 1200 kg, find the magnitude of the normal force exerted by the track on the car at this point.

Solution. There are two forces acting on the car at its topmost point: The normal force exerted by the track and the gravitational force, both of which point downward. Assume that the positive direction is down, and g = +10 m/s².

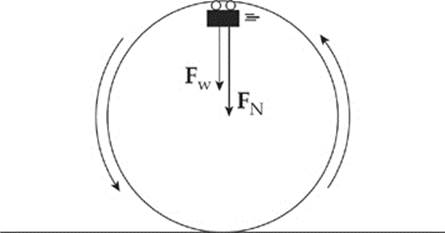
The combination of these two forces, F_N + F_w, provides the centripetal force:

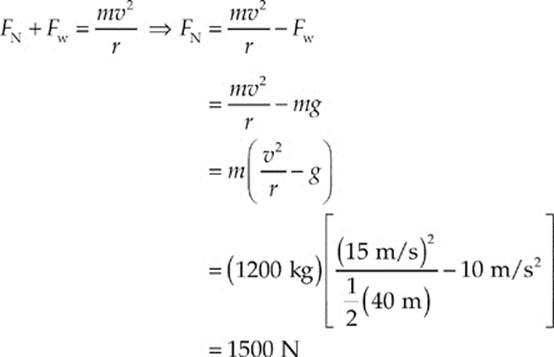
Example 6.5 In the previous example, if the net force on the car at its topmost point is straight down, why doesn”t the car fall straight down?

Solution. Remember that force tells an object how to accelerate. If the car had zero velocity at this point, then it would certainly fall straight down, but the car has a nonzero velocity (to the left) at this point. The fact that the acceleration is downward means that, at the next moment v will point down to the left at a slight angle, ensuring that the car remains on a circular path, in contact with the track.

Example 6.6 How would the normal force change in Example 6.4 if the car was at the bottom of the circle?

Solution. There are still two forces acting on the cart: The gravitational force still points downward but the normal force pushes ninety degrees to the surface (upward). These forces now oppose one another. The combination of these two forces still provides the centripetal force. Because the centripetal acceleration points inward, we will make anything that points toward the center of the circle positive and anything that points away from the circle negative. Therefore our equation becomes:

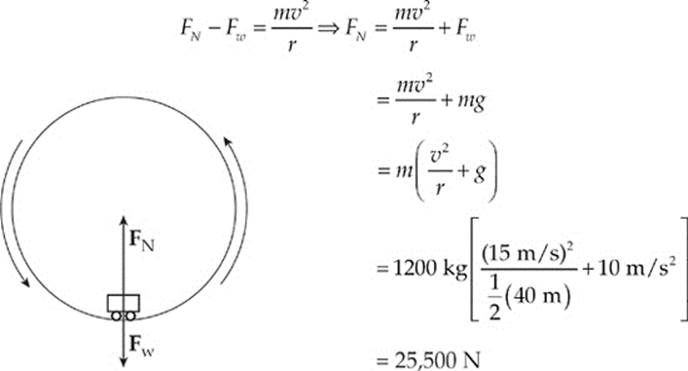
Notice the big difference between this answer and the answer from Example 6.4. This is why you would feel very little force between you and the seat at the top of the loop, but you would feel a big slam at the bottom of the loop.

TORQUE

Intuitively, torque describes the effectiveness of a force in producing rotational acceleration. Consider a uniform rod that pivots around one of its ends, which is fixed. For simplicity, let”s assume that the rod is at rest. What effect, if any, would each of the four forces in the figure below have on the potential rotation of the rod?

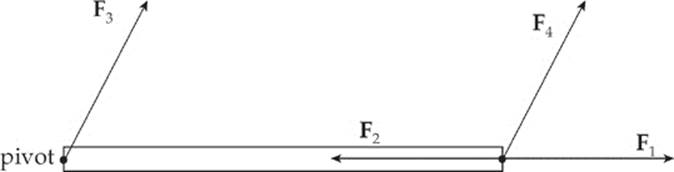
Our intuition tells us the F₁, F₂, and F₃ would not cause the rod to rotate, but F₄ would. What”s different about F₄? It has torque. Clearly, torque has something to do with rotation. Just like a force is a vector quantity that produces linear acceleration, a torque is a vector quantity that produces angular acceleration. Note that, just like for linear acceleration, an angular acceleration is something that either changes the direction of the angular velocity or changes the angular speed. A torque can be thought of as being positive if it produces counterclockwise rotation, or negative if it produces clockwise rotation.

The torque of a force can be defined as follows. Let r be the distance from the pivot (axis of rotation) to the point of application of the force F, and let θ be the angle between vectors r and F.

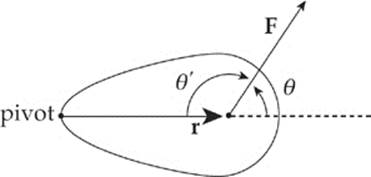
Then the torque of F, denoted by τ (tau), is defined as:

τ = rF sin θ

In the figure above, the angle between the vectors r and F is θ. Imagine sliding r over so that its initial point is the same as that of F. The angle between two vectors is the angle between them when they start at the same point. However, the supplementary angle θ′ can be used in place of θin the definition of torque. This is because torque depends on sin θ, and the sine of an angle and the sine of its supplement are always equal. Therefore, when figuring out torque, use whichever of these angles is more convenient.

We will now see if this mathematical definition of torque supports our intuition about forces F₁, F₂, F₃, and F₄.

The angle between r and F₁ is 0, and θ = 0 implies sin θ = 0, so by the definition of torque, τ = 0 as well. The angle between r and F₂ is 180°, and θ = 180° gives us sin θ = 0, so τ = 0. For F₃, r = 0 (because F₃ acts at the pivot, so the distance from the pivot to the point of application of F₃is zero); since r = 0, the torque is 0 as well. However, for F₄, neither r nor sin θ is zero, so F₄ has a nonzero torque. Of the four forces shown in that figure, only F₄ has torque and would produce rotation.

Example 6.7 A student pulls down with a force of 40 N on a rope that winds around a pulley of radius 5 cm.

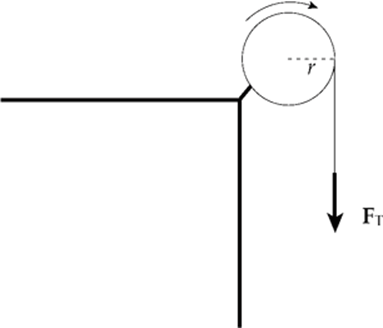
What”s the torque of this force?

Solution. Since the tension force, F_T, is tangent to the pulley, it is perpendicular to the radius vector r at the point of contact:

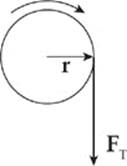
Therefore, the torque produced by this tension force is simply

τ = rF_T = (0.05 m)(40 N) = 2 N·m

Example 6.8 What is the net torque on the cylinder shown below, which is pinned at the center?

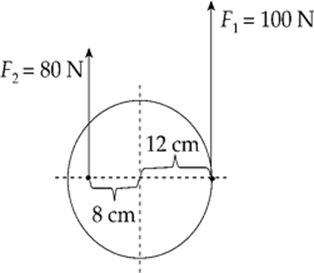
Solution. Each of the two forces produces a torque, but these torques oppose each other. The torque of F₁ is counterclockwise, and the torque of F₂ is clockwise. This can be visualized by imagining the effect of each force, assuming that the other was absent.

The net torque is the sum of all the torques. Counting a counterclockwise torque as positive and a clockwise torque as negative, we have

τ₁ = +r₁F₁ = +(0.12 m)(100 N) = +12 N·m

and

τ₂ = –r₂F₂ = –(0.08 m)(80 N) = –6.4 N·m

τ_net = Στ = τ₁ + τ₂ = (+12 N·m) + (–6.4 N·m) = +5.6 N·m

EQUILIBRIUM

An object is said to be in translational equilibrium if the sum of the forces acting on it is zero; that is, if F_net = 0. Similarly, an object is said to be in rotational equilibrium if the sum of the torques acting on it is zero; that is, if τ_net = 0. The term equilibrium by itself means both translational and rotational equilibrium. A body in equilibrium may be in motion; F_net = 0 does not mean that the velocity is zero; it only means that the velocity is constant. Similarly, τ_net = 0 does not mean that the angular velocity is zero; it only means that it”s constant. If an object is at rest, then it is said to be in static equilibrium.

Example 6.9 A uniform bar of mass m and length L extends horizontally from a wall. A supporting wire connects the wall to the bar”s midpoint, making an angle of 55° with the bar. A sign of mass M hangs from the end of the bar.

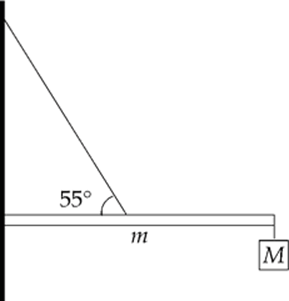
If the system is in static equilibrium and the wall has friction, determine the tension in the wire and the strength of the force exerted on the bar by the wall if m = 8 kg and M = 12 kg.

Solution. Let F_C denote the (contact) force exerted by the wall on the bar. In order to simplify our work, we can write F_C in terms of its horizontal component, F_Cx, and its vertical component, F_Cy. Also, if F_T is the tension in the wire, then F_Tx = F_T cos 55° and F_Ty = F_T sin 55° are its components. This gives us the following force diagram:

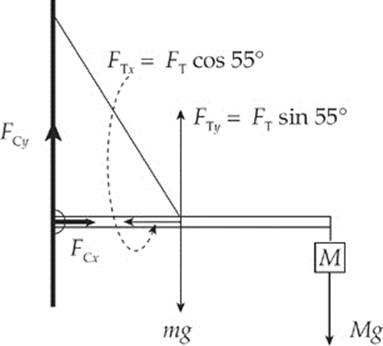
The first condition for equilibrium requires that the sum of the horizontal forces is zero and the sum of the vertical forces is zero:

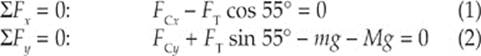
We notice immediately that we have more unknowns (F_Cx, F_Cy, F_T) than equations, so this system cannot be solved as is. The second condition for equilibrium requires that the sum of the torques about any point is equal to zero. Choosing the contact point between the bar and the wall as our pivot, only three of the forces in the diagram above produce torque: F_Ty produces a counterclockwise torque, and both mg and Mg produce clockwise torques, and the sum of the three torques must equal zero. From the definition τ = rFsin0, and taking counterclockwise torque as positive and clockwise torque as negative, we have

This equation contains only one unknown and can be solved immediately:

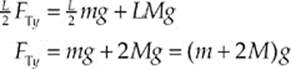
Since F_Ty = F_T sin 55°, we can find that

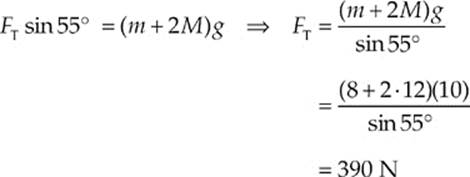
Substituting this result into Equation (1) gives us F_Cx:

And finally, from Equation (2), we get

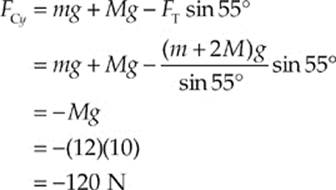
The fact that F_Cy turned out to be negative simply means that in our original force diagram, the vector F_Cy points in the direction opposite to how we drew it. That is, F_Cy points downward. Therefore, the magnitude of the total force exerted by the wall on the bar is

NEWTON”S LAW OF GRAVITATION

Newton eventually formulated a law of gravitation: Any two objects in the universe exert an attractive force on each other—called the gravitational force—whose strength is proportional to the product of the objects” masses and inversely proportional to the square of the distance between them as measured from center to center. If we let G be the universal gravitational constant, then the strength of the gravitational force is given by the equation:

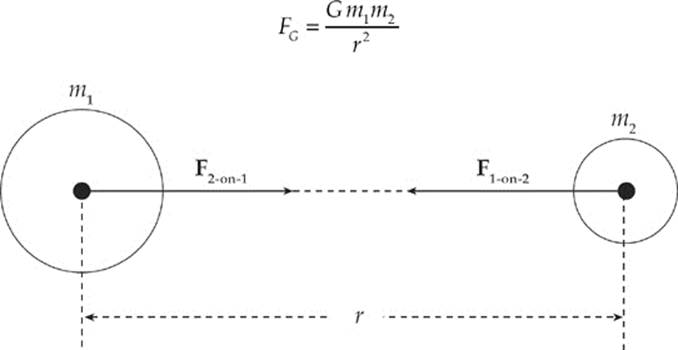
The forces F_1-on-2 and F_2-on-1 act along the line that joins the bodies and form an action/reaction pair.

The first reasonably accurate numerical value for G was determined by Cavendish more than one hundred years after Newton”s Law was published. To three decimal places, the currently accepted value of G is

G = 6.67 × 10^–11 N · m²/kg²

THE GRAVITATIONAL ATTRACTION DUE TO AN EXTENDED BODY

Newton”s Law of Gravitation is really a statement about the force between two point particles; objects that are very small in comparison to the distance between them. Newton also proved that a uniform sphere attracts another body as if all of the sphere”s mass were concentrated at its center.

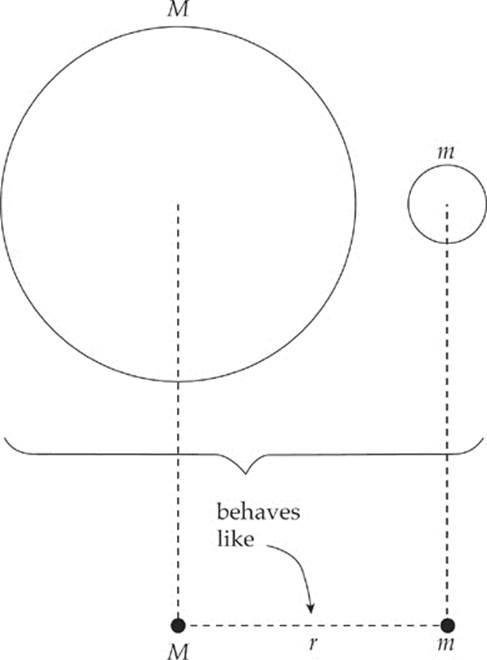
For this reason, we can apply Newton”s Law of Gravitation to extended bodies, that is, to objects that are not small relative to the distance between them.

Additionally, a uniform shell of mass does not exert a gravitational force on a particle inside it. This means that if a spherical planet is uniform, then as we descend into it, only the mass of the sphere underneath us exerts a gravitational force; the shell above exerts no force because we”re inside it.

Example 6.10 Given that the radius of the earth is 6.37 × 10⁶ m, determine the mass of the earth.

Solution. Consider a small object of mass m near the surface of the earth (mass M). Its weight is mg, but its weight is just the gravitational force it feels due to the earth, which is GMm/R². Therefore,

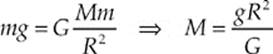
Since we know that g = 10 m/s² and G = 6.67 × 10^–11 N·m²/kg², we can substitute to find

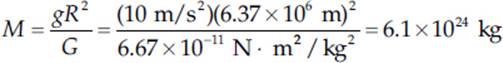
Example 6.11 We can derive the expression g = GM/R² by equating mg and GMm/R² (as we did in the previous example), and this gives the magnitude of the absolute gravitational acceleration, a quantity that”s sometimes denoted g₀. The notation g is acceleration, but with the spinning of the earth taken into account. Show that if an object is at the equator, its measured weight (that is, the weight that a scale would measure), mg, is less than its true weight, mg₀, and compute the weight difference for a person of mass m = 60 kg.

Solution. Imagine looking down at the earth from above the North Pole.

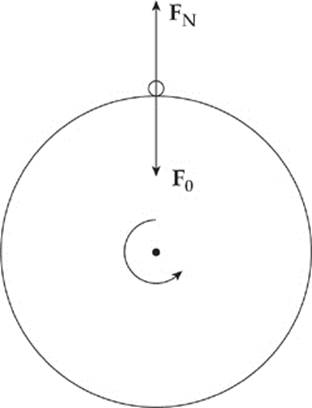
The net force toward the center of the earth is F₀ – F_N, which provides the centripetal force on the object. Therefore,

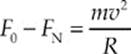
Since v = 2πR/T, where T is the earth”s rotation period we have

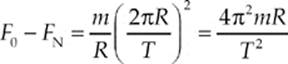
or, since F₀ = mg₀ and F_N = mg,

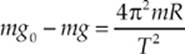
Since the quantity 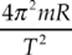is positive, mg must be less than mg₀. The difference between mg₀ and mg, for a person of mass m = 60 kg, is only:

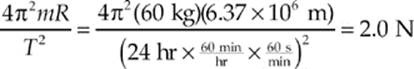
and the difference between g₀ and g is

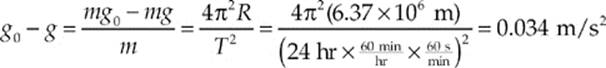
Note that this difference is so small (< 0.3%) that it can usually be ignored.

Example 6.12 Communications satellites are often parked in geosynchronous orbits above Earth”s surface. These satellites have orbit periods that are equal to Earth”s rotation period, so they remain above the same position on Earth”s surface. Determine the altitude that a satellite must have to be in a geosynchronous orbit above a fixed point on Earth”s equator. (The mass of the earth is 5.98 × 10²⁴ kg.)

Solution. Let m be the mass of the satellite, M the mass of Earth, and R the distance from the center of Earth to the position of the satellite. The gravitational pull of Earth provides the centripetal force on the satellite, so

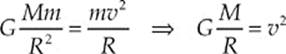
The orbit speed of the satellite is 2πR/T, so

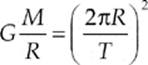
which implies that

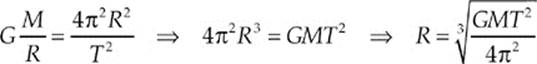
Now the key feature of a geosynchronous orbit is that its period matches Earth”s rotation period, T = 24 hr. Substituting the numerical values of G, M, and T into this expression, we find that

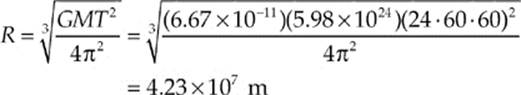
Therefore, if r_E is the radius of Earth, then the satellite”s altitude above Earth”s surface must be

h = R – r_E = (4.23 × 10⁷ m) – (6.37 × 10⁶ m) = 3.59 × 10⁷ m

Example 6.13 An artificial satellite of mass m travels at a constant speed in a circular orbit of radius R around the earth (mass M). What is the speed of the satellite?

Solution. The centripetal force on the satellite is provided by Earth”s gravitational pull. Therefore,

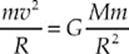
Solving this equation for v yields

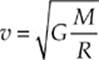
Notice that the satellite”s speed doesn”t depend on its mass; even if it were a baseball, if its orbit radius were R, then its orbit speed would still be .

CHAPTER 6 REVIEW QUESTIONS

Solutions can be found in Chapter 18.

SECTION I: MULTIPLE CHOICE

1. An object moves at constant speed in a circular path. Which of the following statements is/are true?

I. The velocity is constant.

II. The acceleration is constant.

III. The net force on the object is zero.

(A) II only

(B) I and III only

(D) I and II only

(E) None of the above

Questions 2–3:

A 60 cm rope is tied to the handle of a bucket which is then whirled in a vertical circle. The mass of the bucket is 3 kg.

2. At the lowest point in its path, the tension in the rope is 50 N. What is the speed of the bucket?

(A) 1 m/s

(B) 2 m/s

(D) 4 m/s

(E) 5 m/s

3. What is the critical speed below which the rope would become slack when the bucket reaches the highest point in the circle?

(A) 0.6 m/s

(B) 1.8 m/s

(D) 3.2 m/s

(E) 4.8 m/s

4. An object moves at a constant speed in a circular path of radius r at a rate of 1 revolution per second. What is its acceleration?

(A) 0

(B) 2π²r

(D) 4π²r

(E) 4π²r²

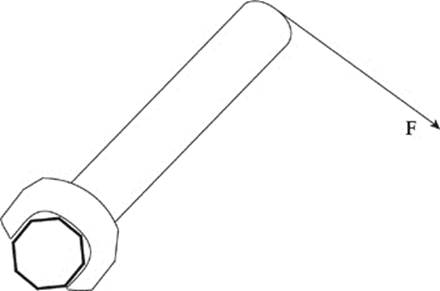
In an effort to tighten a bolt, a force F is applied as shown in the figure above. If the distance from the end of the wrench to the center of the bolt is 20 cm and F = 20 N, what is the magnitude of the torque produced by F?

(A) 0 N·m

(B) 1 N·m

(D) 4 N·m

(E) 10 N·m

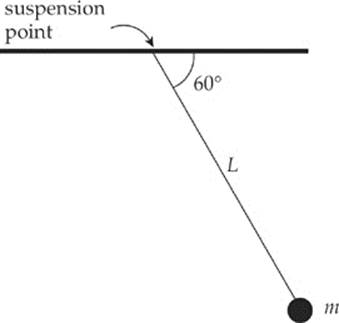
In the figure above, what is the torque about the pendulum”s suspension point produced by the weight of the bob, given that the length of the pendulum, L, is 80 cm and m = 0.50 kg?

(A) 0.5 N·m

(B) 1.0 N·m

(D) 2.0 N·m

(E) 3.4 N·m

A uniform meter stick of mass 1 kg is hanging from a thread attached at the stick”s midpoint. One block of mass m = 3 kg hangs from the left end of the stick, and another block, of unknown mass M, hangs below the 80 cm mark on the meter stick. If the stick remains at rest in the horizontal position shown above, what is M?

(A) 4 kg

(B) 5 kg

(D) 8 kg

(E) 9 kg

8. If the distance between two point particles is doubled, then the gravitational force between them

(A) decreases by a factor of 4

(B) decreases by a factor of 2

(D) increases by a factor of 4

(E) cannot be determined without knowing the masses

9. At the surface of the earth, an object of mass m has weight w. If this object is transported to an altitude that”s twice the radius of the earth, then, at the new location,

(A) its mass is m/2 and its weight is w/2

(B) its mass is m and its weight is w/2

(D) its mass is m and its weight is w/4

(E) its mass is m and its weight is w/9

10. A moon of mass m orbits a planet of mass 100m. Let the strength of the gravitational force exerted by the planet on the moon be denoted by F₁, and let the strength of the gravitational force exerted by the moon on the planet be F₂. Which of the following is true?

(A) F₁ = 100F₂

(B) F₁ = 10F₂

(D) F₂ = 10F₁

(E) F₂ = 100F₁

11. The dwarf planet Pluto has 1/500 the mass and 1/15 the radius of Earth. What is the value of g (in m/s²) on the surface of Pluto?

(A)

(B)

(C)

(D)

(E)

12. A satellite is currently orbiting Earth in a circular orbit of radius R; its kinetic energy is K₁. If the satellite is moved and enters a new circular orbit of radius 2R, what will be its kinetic energy?

(A)

(B)

(D) 2K₁

(E) 4K₁

13. A moon of Jupiter has a nearly circular orbit of radius R and an orbit period of T. Which of the following expressions gives the mass of Jupiter?

(A)

(B)

(C)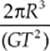

(D)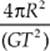

(E)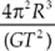

14. Two large bodies, Body A of mass m and Body B of mass 4m, are separated by a distance R. At what distance from Body A, along the line joining the bodies, would the gravitational force on an object be equal to zero? (Ignore the presence of any other bodies.)

(A)

(B)

(C)

(D)

(E)

15. You are looking at a top view of a planet orbiting the Sun in a clockwise direction. Which of the following would describe the velocity, acceleration, and force acting on the planet due to the Sun”s pull at point P?

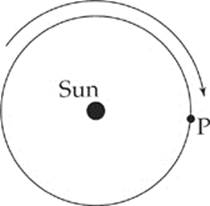
(A) v ↓ a ↑ F ↑

(B) v ↓ a ← F ←

(D) v ← a ↓ F ↓

(E) v ↑ a ← F ←

16. Which of the following statements are true for a satellite in outer space orbiting the earth?

I. There are no forces acting on the satellite.

II. The force of gravity is the only force acting on the satellite.

III. The force of gravity is balanced by the outward force of the object.

(A) I only

(B) II only

(D) either I or III may be correct

(E) either II or III may be correct

SECTION II: FREE RESPONSE

1. A robot probe lands on a new, uncharted planet. It has determined the diameter of the planet to be 8 × 10⁶ m. It weighs a standard 1 kg mass and determines that 1 kg weighs only 5 Newtons on this new planet.

(a) What must the mass of the planet be?

(b) What is the acceleration due to gravity on this planet? Express your answer in both m/s² and g”s (where 1 g = 10 m/s²).

(d) This planet has a moon that orbits it at a distance 6 × 10⁹ m from center to center. What is the moon”s period?

2. The earth has a mass of 6 × 10²⁴ kg and orbits the sun in 3.15 × 10⁷ seconds at a constant circular distance of 1.5 × 10¹¹ m.

(a) What is the earth”s centripetal acceleration around the Sun?

(b) What is the gravitational force acting between the Sun and Earth?

3. An amusement park ride consists of a large cylinder that rotates around its central axis as the passengers stand against the inner wall of the cylinder. Once the passengers are moving at a certain speed v, the floor on which they were standing is lowered. Each passenger feels pinned against the wall of the cylinder as it rotates. Let r be the inner radius of the cylinder.

(a) Draw and label all the forces acting on a passenger of mass m as the cylinder rotates with the floor lowered.

(b) Describe what conditions must hold to keep the passengers from sliding down the wall of the cylinder.

4. A curved section of a highway has a radius of curvature of r. The coefficient of friction between standard automobile tires and the surface of the highway is μ_s.

(a) Draw and label all the forces acting on a car of mass m traveling along this curved part of the highway.

(b) Compute the maximum speed with which a car of mass m could make it around the turn without skidding in terms of μ_s, r, g, and m.

City engineers are planning on banking this curved section of highway at an angle of θ to the horizontal.

(c) Draw and label all of the forces acting on a car of mass m traveling along this banked turn. Do not include friction.

(d) The engineers want to be sure that a car of mass m traveling at a constant speed v (the posted speed limit) could make it safely around the banked turn even if the road were covered with ice (that is, essentially frictionless). Compute this banking angle θ in terms of r, v, g, and m.

SUMMARY

· For objects undergoing uniform circular motion, the centripetal acceleration is given by a_c = and the centripetal force is given by F_c = .

· Torque is a turning force that makes an object rotate. The equation for torque is τ = rF sin θ. Torques may be clockwise or counterclockwise. An object is in equilibrium if ΣF_x = 0, ΣF_y = 0, and Στ = 0.

· For any two masses in the universe there is a gravitational attraction given by:

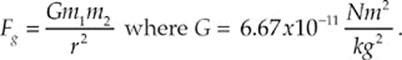
· The acceleration due to gravity on any planet is given by:

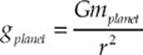
· Many times universal gravitation is linked up with circular motion (because planetary orbits are very nearly circular). Therefore, it is useful to keep the following equations for circular motion mentally linked for those questions that include orbits: