Homework Helpers: Physics
4 Rotational and Circular Motion
Lesson 4–6: Kepler”s Laws and the Motion of Satellites
When it comes to the motion of planets and other satellites, Johannes Kepler (1571–1630) wrote the rules. By assuming that the planetary orbits were elliptical, rather than circular, he was able to make data that had been collected earlier by Tycho Brahe (1546–1601) and other astronomers fit. You might wonder why we will discuss these elliptical orbits in a chapter about circular motion. One reason is because the gravitational force of attraction between the sun and a planet provides the centripetal force that keeps the planet in orbit, so that provides a connection to what we discussed in the previous lessons. Another reason is because if we treat the orbits of planets and other satellites as circular, we are able to come up with close approximations of their speeds and distances.
Kepler”s First Law
The orbits of the planets are ellipses, with the sun at one focus of the ellipse.
Before Kepler, supporters of the Copernican heliocentric model of the solar system required a complex system of larger and smaller circles (orbits and epicycles) to account for the observed relative positions of the planets. From his observations of Mars, Kepler came to realize that the orbits of the planets were elliptical, allowing him to construct a model for the solar system that did not require epicycles.
Kepler”s Second Law
The line joining the planet to the sun sweeps out equal areas in equal times as the planet travels around the ellipse.
As a planet moves about its elliptical orbit, with the sun at one focus, the distance between it and the sun is constantly changing. The position in the planetary orbit that brings the planet closest to the sun is called perihelion. The position farthest from the sun is called aphelion. In order for the planet to sweep out equal areas in equal times, it must move fastest at the perihelion and slowest at the aphelion.
Kepler”s Third Law
The ratio of the squares of the revolutionary periods for two planets is equal to the ratio of the cubes of their semimajor axes.
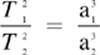
The semimajor axis is half of the major axis, which, in turn, is the line that bisects the ellipse the long way. In other words, the semimajor axis is half of the longest axis of the ellipse.
Kepler”s third law states that the ratio, T 2/a 3, is the same for every planet.
Lesson 4–6 Review
1. What provides the centripetal force that keeps the Earth in orbit around the sun?
2. The position in a planetary orbit that brings it closes to the sun is called__________________.