Homework Helpers: Physics

4 Rotational and Circular Motion

I have heard it said that “Newton discovered gravity,” which seems to suggest that there was no gravity before him. What Newton really did was show that it was the force of gravity that keeps the moon in orbit around Earth, and all of the planets in orbit around the sun. He went further to state that every object in the universe exerts a gravitational force on every other object in the universe. So all things, including you, can be thought to have a gravitational field around it. The force of gravitational attraction between two objects is proportional to the product of the masses of the objects, and inversely proportional to the square of the distance between them (measured from center of mass to center of mass). A proportionality constant (G), called the universal gravitational constant, has been added to the equation to allow for accurate calculations. The current value for G is approximately 6.67 × 10^–11 N · m²/kg².

Universal Gravitational Constant

G = universal gravitational constant = 6.67 × 10^–11 N · m²/kg²

One of the important things to keep in mind when studying the universal law of gravitation is that Newton”s other laws are still in effect. We study these laws in isolation, but they exist all together. This means that Newton”s third law, the law of action-reaction, plays an important part in the gravitational attraction between two bodies. If object a exerts a force of gravitational attraction on object b, object b exerts an equal and opposite force of gravitational attraction on object a. As we mentioned in Chapter 2, as hard as Earth is pulling you down, you are pulling the Earth up. As the Earth is pulling the moon toward it, the moon is pulling the earth with an equal and opposite force, causing tides.

Gravity is an example of a field force, or a force that acts over a distance. As you know, gravity can act over enormous distances, even allowing the sun to keep Earth in orbit. It is often useful to imagine the gravitational field around an object. As an object moves “deeper” into another gravitational field, it experiences a greater force. This explains why we weigh slightly more on the surface of Earth than we would on an airplane.

In a field diagram such as this one, the arrows indicate the direction of the force that an object will experience inside the field. The closer together the lines are at a given point, the greater the field strength at that point. As you can see, the lines get farther apart and the field gets weaker as you move away from the planet.

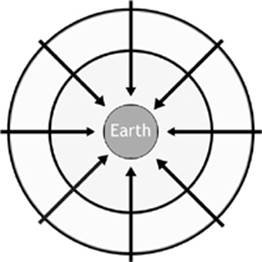
Figure 4.6

Newton”s universal law of gravitation equation can be used to find the mass of unknown bodies, or the acceleration due to gravity (g) on other planets. This leads to many interesting problems in this area of study.

Example 1

Calculate the gravitational force of attraction between a 35.0 kg girl and a 1.20 × 10³ kg car when they are separated by a distance of 3.45 m.

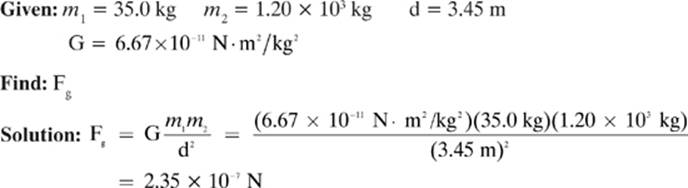
Even if you were initially surprised to learn that all objects exert a gravitational force of attraction on all other objects, our answer for Example 1 should make you realize why we don”t attract macroscopic objects in the same way that a very powerful magnet will draw nails or paper clips to it. The car in Example 1 may be considered a relatively massive object, and the distance between the girl and the car isn”t far, but the attraction between the two due to gravity is only 2.35 × 10⁻⁷N or 0.000000235 N! Such a small force is not going to be enough to overcome the force of friction between the objects and the ground to draw them together.

You should always keep in mind that the gravitational force of attraction between two objects is inversely proportional to the square of the distance between their centers of mass. This means that if you halve the distance between two objects, you quadruple the force of gravity between them. If you triple the distance between the objects, you will decrease the force of gravity between them by a factor of (3² = 9) 9.

Example 2

Two objects separated by a distance of 4.0 cm exert a force of attraction due to gravity of 1.0 N on each other. What would be the gravitational force of attraction between these two objects if the distance between them was decreased to 1.0 cm?

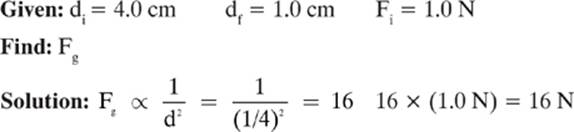
Example 3

The moon has a mass of approximately 7.349 × 10²² kg and a diameter of approximately 3476 kilometers. What would be the value of g near the surface of the moon?

Remember: The distance (d) that you need is measured to the center of the object, which would be the radius of the moon. The radius is half the diameter, so we find d:

You have probably heard that you would weigh 1/6th of your Earth weight on the moon, and now you have calculated it. Note:

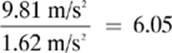
Now try the review questions.

Lesson 4–5 Review

1. ________________ is a force that acts on objects without touching them.

2. An object has a weight of 200 N on the surface of Earth. How much would it weigh if its distance from the center of Earth were doubled?

3. Earth has a mass of approximately 5.97 × 10²⁴ kg, and a radius of approximately 6.37 × 10⁶ m. How much would a man who weighs 785 N on the surface of Earth weigh if he was flying in an airplane at an altitude of 1.00 × 10⁴ meters? (Assume the plane is flying level, at a constant speed.)