SAT Physics Subject Test

Chapter 6 Curved and Rotational Motion

EQUILIBRIUM

An object is said to be in translational equilibrium if the sum of the forces acting on it is zero—that is, if F_net = 0. Similarly, an object is said to be in rotational equilibrium if the sum of the torques acting on it is zero—that is, if τ_net = 0. The term equilibrium by itself means both translational and rotational equilibrium. An object in equilibrium may be in motion. F_net = 0 does not mean that the velocity is zero, it only means that the velocity is constant. Similarly, τ_net = 0 does not mean that the angular velocity is zero; it only means that it”s constant. If an object is at rest, then it is said to be in static equilibrium.

The Skinny on Equilibrium

Translational equilibrium means

F_net = 0 a = 0 v is constant.

Rotational equilibrium means

τ_net = 0 τ_clockwise = τ_{counterclockwise}.

Equilibrium means both rotational and translational equilibrium are true.

11. A block of mass M shown in the figure below hangs motionless. What”s the tension in each of the ropes?

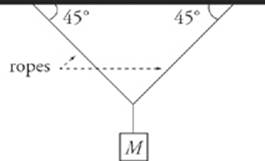
Here”s How to Crack It

Let T₁ be the tension in the left-hand rope and let T₂ be the tension in the right-hand rope. We”ll write each of these forces in terms of their horizontal and vertical components.

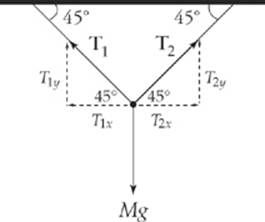
Look at the point where the two ropes meet. Since the system is in static equilibrium, the net force on this point must be zero. This means the horizontal forces must balance and the vertical forces must balance. Since the horizontal forces balance, this means T_1x = T_2x, so

T₁ cos 45° = T₂ cos 45°

which gives us T₁ = T₂. Since the tensions are the same, we can drop the subscripts and simply refer to the tension in each rope as T.

Now, to balance the vertical forces, we notice that the total upward is T_1y + T_2y = T_y + T_y = 2T_y and the force downward is Mg, the weight of the block. Therefore,

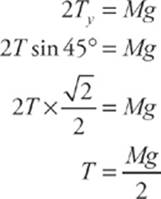
This gives us the tension in each of the ropes noted in the figure.

12. The figure below shows a homogeneous bar of mass M and length L, with one end attached to a hinge on a wall and the other end supported by a string. What”s the tension in the string?

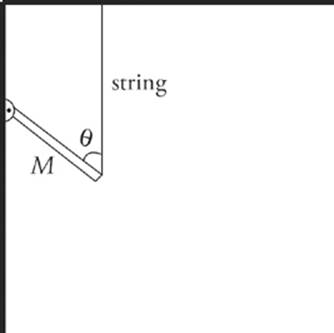
Here”s How to Crack It

Let T be the tension in the string, let L be the length of the bar. The weight of the bar acts at the center of mass (halfway down the bar) so the force diagram looks like the following:

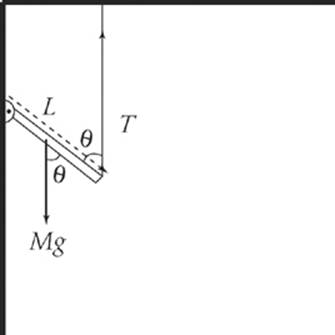
Look at the point where the bar is attached to the wall. Since the system is in static equilibrium, the net torque about this point must be zero. The weight of the bar produces a clockwise torque, of magnitude (L/2) Mg sin θ, and the tension in the string produces a counterclockwise torque, of magnitude LT sin θ. Since these torques balance, we have

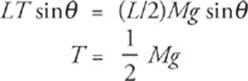
There is a force acting on the rod by the wall, but since that point is taken to be the pivot, its torque = 0. This “wall force” could, in theory, have both an x- and a y-component, depending on what is needed to make sure the rod doesn”t move. Since there are no other x forces in this example, there will be no x-component of the wall force.