SAT Subject Test Physics (2012)
PART III. PHYSICS TOPIC REVIEW
Chapter 19. SPECIAL RELATIVITY
For everyday observations, Newton’s laws of motion provide good approximations for describing and predicting motion. If the speed of a particle approaches the speed of light, however, a different approach is required to interpret motion. In this chapter, you will review Einstein’s approach to describing motion.
Einstein’s Special Theory of Relativity
Objects traveling at speeds that are significant fractions of the speed of light are known as relativistic objects. Einstein proposed his special theory of relativity to describe the motion of relativistic objects. His theory results from two basic postulates:
1. The speed of light is constant in all reference frames, despite any relative motion between an observer and the light source.
2. The laws of physics are the same in all inertial reference frames.
First Postulate The first postulate can be a little difficult to accept at first. After all, if a car drives away from a parked car at 50 km/h, you describe the speed of the car accordingly. If, instead, two cars are moving in opposite directions at 50 km/h, each one appears to be moving away from the other at 100 km/h. The speed of each car relative to the other depends on the motion of both cars.
What the first postulate says is that relative motion does not affect the speed of light. If you turn on a light toward an observer, the observer will measure the speed of light c as 3.0 × 108 m/s. If the observer approaches you at a high rate of speed, the observer would still measure the same speed of light. If you move toward the observer, the observer would again measure the same speed of light.
Second Postulate The second postulate is a lot easier to accept because it is a basic rule of science. An inertial reference frame is one that is not accelerating. In other words, it is at rest or moving at a constant speed in a straight line. In this type of reference frame, the same laws describe motion. So, for example, a force will have the same effect on an object regardless of what caused the force and where the object is.
As you review Einstein’s special theory of relativity, keep two points in mind. The first is that Einstein’s theory did not replace Newton’s laws of motion. Newton’s laws continue to serve as a particular case of Einstein’s theory, which is motion at speeds that do not approach the speed of light. The second is that Einstein’s law of general relativity is different from special relativity, and it involves the gravitational force.
Length Contraction
An interesting result of special relativity is that although observers moving relative to one another must agree on the speed of light, they do not have to agree on measurements of length. An observer at rest relative to a moving object traveling at relativistic speeds would observe the length of the object to be shorter than it would be at rest relative to the observer. This phenomenon is known as length contraction, and the amount of contraction depends on the object’s speed relative to the observer. The faster the speed is, the greater the contraction is. At normal everyday speeds, the effect is very small. Near the speed of light, however, the contraction becomes more pronounced.
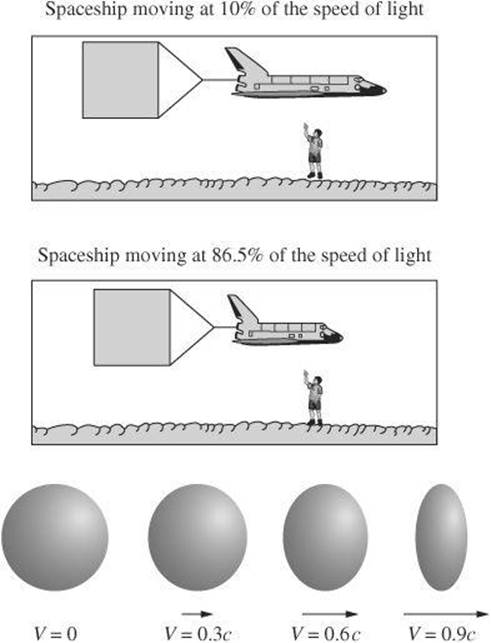
Consider a rod of length L in a stationary frame of reference and a moving frame of reference. The observer will measure the length of the rod in the moving frame of reference Lo as shorter than in the stationary frame of reference. The difference can be found according to the following equation.
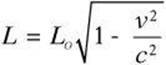
Be aware that the dilation is only in the direction of motion. If, for example, motion is from left to right, length contraction occurs in this direction only. It does not occur in the vertical direction.
Time Dilation
Just as length is contracted, time is stretched out under relativistic conditions. In other words, moving clocks run slow. This phenomenon is known as time dilation.
If the length between two ticks of a clock is measured, an observer moving relative to the clock will measure the time as longer than an observer who is stationary when compared with the clock. The relationship between time in a moving frame of reference T to time in a stationary frame of reference To is described by the following equation.
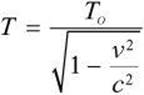
Relativistic Mass and Energy
Unlike in Newtonian mechanics, the inertial mass of a relativistic object varies with velocity. The mass m can be described by the following equation, where mo is the mass in a stationary frame of reference.
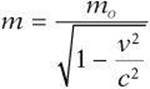
As part of this theory of special relativity, Einstein also presented his now famous equation to relate energy to relativist mass.
![]()
According to this equation, energy and mass are different manifestations of the same thing. A small amount of mass, because it is multiplied by the square of the speed of light, can result in a tremendous amount of energy.
Test-Taking Hint
Plan out your study schedule so that you have enough time to review all the concepts and study any topics with which you have difficulty. If you leave too much until the last minute, you may become frustrated and confused by more complex topics such as relativity.
REVIEW QUESTIONS
Select the choice that best answers the question or completes the statement.
1. Which of the following is a postulate of Einstein’s special theory of relativity?
(A) The acceleration of an object is directly proportional to the force exerted on it.
(B) The speed of light is constant in all reference frames.
(C) An object’s inertia is a measure of its mass.
(D) Time is constant for all observers regardless of relative motion.
(E) Objects do not have mass at the speed of light.
2. A rod is moving at a velocity of 0.6c. How does its length in a stationary frame of reference Lo compare to its length in a moving frame of reference L?
![]()
![]()
![]()
![]()
![]()
3. What is the length of a meter stick if it is moving with a velocity of 0.8c relative to Earth?
(A) 0.36 m
(B) 0.48 m
(C) 0.60 m
(D) 0.80 m
(E) 1.2 m
4. A muon at rest has a lifetime of about 2.2 microseconds. How long is the lifetime of a muon traveling at 0.995c?
(A) 2.3 μs
(B) 10 μs
(C) 22 μs
(D) 115 μs
(E) 220 μs
5. What is the rest energy of a 5.0-kg rock?
![]()
![]()
![]()
![]()
![]()
QUESTION ANSWERS AND EXPLANATIONS
1. B Only choice B is correct. The other statements do not describe relativistic motion.
2. E Substitute the given information into the equation for length dilation.
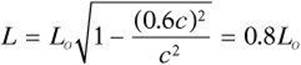
3. C Substitute the given velocity and the length of a meter stick into the equation for length dilation:
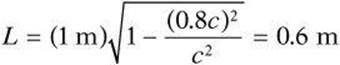
4. C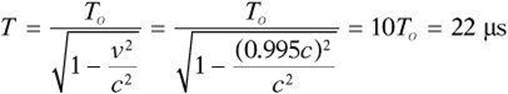
5. E ![]()