SAT Subject Test Physics (2012)

PART III. PHYSICS TOPIC REVIEW

Chapter 4. DYNAMICS

Describing the motion of an object, or kinematics, is closely related to understanding why something moves the way it does, or dynamics. The key to dynamics is a thorough understanding of forces, and, in particular, Newton’s laws of motion.

Introduction to Forces

You exert a force whenever you lift a book, open a door, or throw a ball. A force is a push or pull. Forces are vector quantities with both magnitude and direction. The SI unit of force is the newton. Therefore, a force might be 10 newtons acting to the north or 2 newtons acting to the east.

As vectors, forces can be added and combined using the rules of vectors presented in Chapter 2. Recall that vectors could cancel out. If the forces acting on an object cancel out, the forces are said to be balanced forces. The overall, or net force, is zero. Unbalanced forces exist when the forces on an object do not cancel out. In this case, the net force is not zero.

It is helpful to be familiar with several common forces. Even if you are not asked to describe them explicitly, an understanding of their nature will be expected within several questions of SAT Physics. Other forces will be discussed as they are reviewed in later chapters.

Gravitational Force As you read these words, you are being pulled by the gravitational force, which is the force of attraction between every pair of masses in the universe. The measure of the gravitational force exerted on an object is weight. Your weight, for example, is a measure of the gravitational force Earth exerts on you. Make sure you do not confuse weight with mass, as often occurs. Mass is the amount of matter in an object. It is a scalar quantity that is independent of location. Weight, however, is a vector quantity that varies with the gravitational force acting on an object. The mass of a ball on Earth is the same as its mass on the moon because the amount of matter in it does not change. The weight of the ball on the moon, however, is much less than its weight on Earth because the gravitational force exerted by the moon is about one-sixth the gravitational force exerted by Earth.

The weight of an object is the product of the mass of the object and the acceleration due to gravity, g. For example, the following equation shows the calculation for the weight of a 50-kg mass on Earth. Note that weight can be represented by F_weight or W.

Normal Force In everyday language, the word normal might mean ordinary or usual. In physics, however, the word has a very specific meaning. The normal is a line perpendicular to a surface. The normal force, therefore, is a force that acts perpendicular to a surface of contact between two objects. The normal force is equal in magnitude, but opposite in direction, to the weight of an object. The normal force can be represented as F_normal or N.

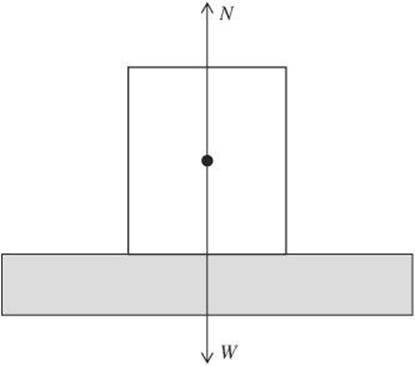
Friction When you rub sandpaper across a piece of wood, friction is created. Friction is a force between materials that are in contact with one another. The force of friction acts parallel to the plane of contact between the two materials and acts in the direction opposite to the direction of the object being moved. The surfaces do not have to be as rough as sandpaper for friction to be created. Even surfaces that seem smooth to the unaided eye are rough at the microscopic level and establish friction.

There are two basic types of friction: static friction and kinetic friction. Static friction is the force that arises between two surfaces that are not moving relative to one another. For example, suppose you push a dresser that is at rest on a floor. Static friction resists your force and holds the dresser in place. In the following diagram, you can see that the force of your push, F_push, is equal and opposite to the force of static friction, F_static.

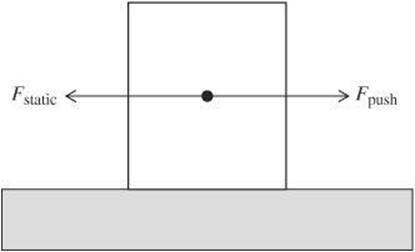
Static friction occurs when the net force on the object is zero, and therefore, the object is at rest. Once the force of the push overcomes the force of static friction, the net force is no longer zero and the object is set in motion. Kinetic friction is the force that arises between two surfaces that are moving relative to one another.

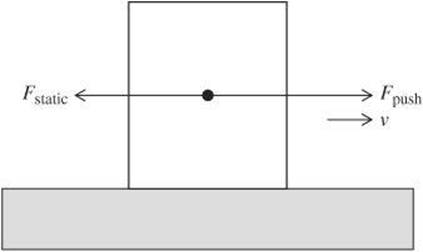
Once static friction is overcome and the object begins to move, the relationship between the force of kinetic friction, F_kinetic, and the force of the push, F_push, determines the specifics of the motion of the object. If F_push is equal in magnitude to F_kinetic, the net force again becomes zero and the object moves at constant velocity. If F_push is greater in magnitude than F_kinetic, as in the following diagram, there is a net force in the direction of motion so the object accelerates. If F_push is lower in magnitude than F_kinetic, there is a net force, but it is opposite to the direction of motion. Therefore, the object will slow down and come to a stop.

The magnitude of the friction force depends on the nature of the surfaces in contact and the normal force. The ratio of the force of friction between two bodies is known as the coefficient of friction and is represented by the Greek letter μ. The coefficients are constants that vary with the material and have both static (μ_s) and kinetic components (μ_k). The value of μ always falls between 0 and 1, with lower values indicating smoother surfaces. In addition, the coefficient of kinetic friction will always be less than the coefficient of static friction for a given surface. Questions on SAT Physics may provide you with the coefficient of friction and ask you to calculate the resulting friction force.

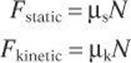
Newton’s Laws of Motion

In 1686, Isaac Newton presented three laws of motion that, summarize the relationship between force and motion.

First Law of Motion A body at rest remains at rest and a body in motion will remain in motion at constant velocity unless acted upon by an unbalanced force.

The first part of this law may seem obvious. A book at rest on a desk does not move unless you push it. Similarly, a ball does not move unless you throw it, and a leaf does not move unless the wind blows it. In other words, an object does not move unless an unbalanced force acts on it to change its speed or direction.

The second part of this law requires a little more consideration. It suggests that once an object is moving, it will continue to move in the same way unless an unbalanced force acts on it. Yet you know that a soccer ball kicked across a field and a toy car pushed across a floor eventually come to a stop. Now you know that if an object in motion comes to a stop, an unbalanced force must be acting on it. In the case of the soccer ball and the toy car, that force is friction. If friction were not present, objects would continue to travel with constant motion forever.

Another way to state Newton’s first law of motion is that the velocity of the object does not change if the net force acting on the object is zero. Remember that velocity involves both speed and direction. So when a body is at rest or moving with constant speed in a straight line, the resultant of all the forces acting on the body must be zero. That does not require that there be no forces acting on the body. Instead, any forces acting on the body must combine in such a way that the net force is zero.

The resistance to any change in the motion of an object is known as inertia. Therefore, Newton’s first law is also known as the law of inertia.

Second Law of Motion The acceleration of an object is directly proportional to the net force exerted on it and inversely proportional to its mass.

What this law means is that if the net force acting on an object is not zero, the object will be accelerated. The direction of acceleration will be the same as the direction of the force. The magnitude of the acceleration will depend on the magnitude of the force and the mass of the object.

You may know from experience that you have to use more force to accelerate a shopping cart by the same amount when it is filled than when it is empty. That’s because the mass of the cart increases as it is filled, so a greater force is required to produce the same amount of acceleration. If you increase the force you exert without changing the mass, the acceleration increases.

Newton’s second law can be represented by the following equation.

where F is force, m is mass, and a is acceleration. In the SI system, force is measured in newtons, mass in kilograms, and acceleration in m/s². This equation is often rewritten in a form with which you may be more familiar.

Written this way, you can see that one newton is the force needed to accelerate a 1-kilogram object by 1 meter per second per second.

Example:

A. A car has a mass of 1000 kg. What force is required to accelerate the car 0.05 m/s²?

B. What force would be required to accelerate a truck with a mass of 10,000 kg by the same amount?

A greater force is required to achieve the same acceleration because the mass of the truck is greater than the mass of the car.

C. What force would be required to accelerate the car 0.5 m/s²?

A greater force is required to accelerate the same mass, the car, by a greater amount.

Third Law of Motion For every action, there is an equal and opposite reaction.

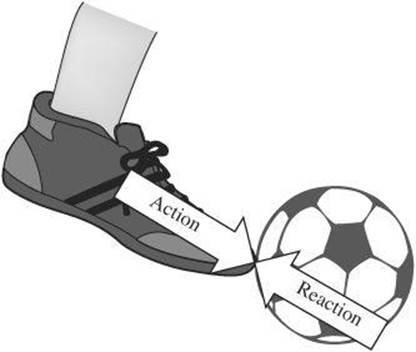
This law explains that whenever one object exerts a force on a second object, the second object exerts a force on the first object that is equal in magnitude but opposite in direction. Unlike balanced forces, the two forces do not cancel because they do not act on the same object. As a result, the forces can lead to a change in the motion of the objects. The following diagram shows that a foot exerts a force on a soccer ball (action). The soccer ball exerts an equal and opposite force on the foot (reaction). Be aware that the names of the forces are somewhat arbitrary in that they occur simultaneously rather than sequentially.

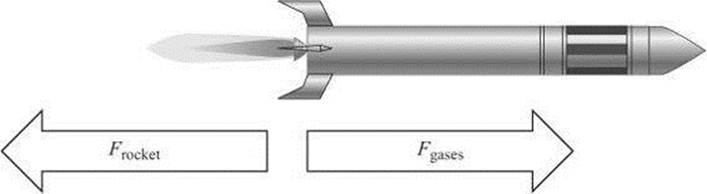
There are numerous examples of Newton’s third law of motion. For example, consider the rocket in the following diagram. When it burns fuel, gases are expelled out of the bottom. The action force can be considered the force exerted on the gases away from the rocket. The gases, in turn, exert an equal but opposite force on the rocket. This reaction force propels the rocket forward. The force exerted by the rocket F_rocket is exactly equal in magnitude and opposite in direction to the force exerted by the gases F_gases.

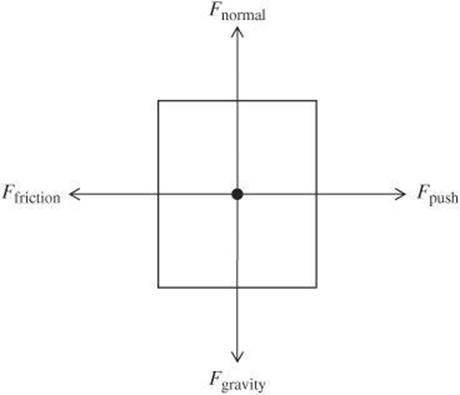
Free-Body Diagrams

Many of the diagrams you have been analyzing are special versions of vector diagrams known as free-body diagrams. Diagrams such as these are commonly used to compare the magnitudes and directions of all the forces acting on an object. The length of the arrow represents the magnitude of the force, and the direction of the arrow indicates the direction in which the force is being exerted. Although they can vary somewhat, most free-body diagrams represent the object as a square with arrows extending from its center. The arrows are labeled to indicate the type of force.

Test-Taking Hint

The SAT Physics exam will not ask you to draw diagrams. However, questions might require that you either interpret free-body diagrams or recognize the correct diagram from a group of choices. Make sure you understand all of the information presented in such a diagram so that you do not overlook seemingly minor differences between diagrams.

REVIEW QUESTIONS

Select the choice that best answers the question or completes the statement.

1. Which combination of forces on an object results in a net force of zero?

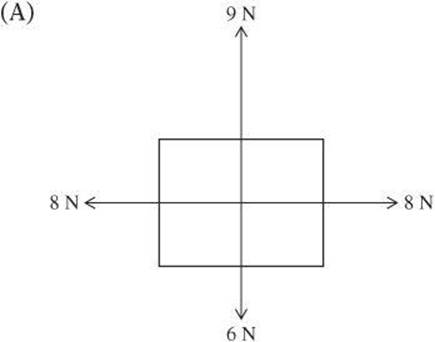
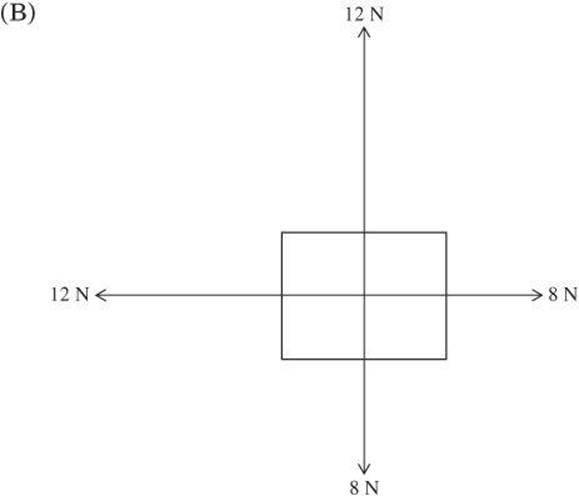
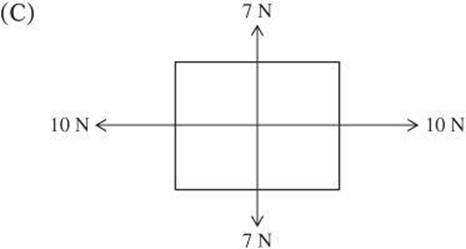
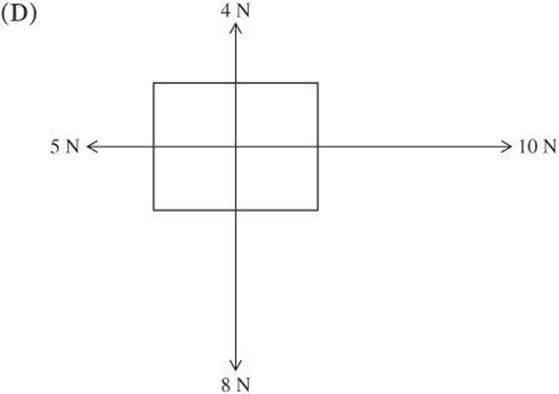
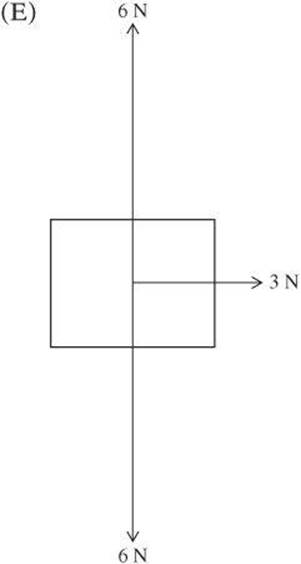
2. A metal box is located on a table in a factory. The box has a weight of 32 N, and a machine pushes down on the box with a force of 20 N. What is the normal force on the box?

(A) 12 N

(B) 20 N

(C) 32 N

(D) 52 N

(E) 70 N

3. The weight of an object on Earth is 147 N. What is its approximate mass?

(A) 5 kg

(B) 10 kg

(C) 15 kg

(D) 20 kg

(E) 25 kg

4. If the net force exerted on a body is doubled while the mass remains the same, the acceleration of the body is

(A) halved

(B) doubled

(C) unchanged

(D) quartered

(E) quadrupled

5. The net force on the object shown below is

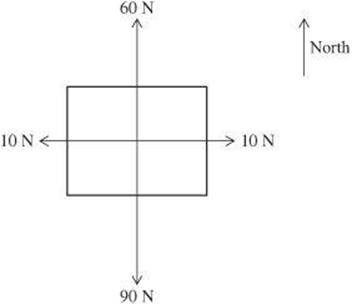
(A) 30 N southward

(B) 50 N northward

(C) 75 N southeast

(D) 80 N southwest

(E) 150 N southward

6.

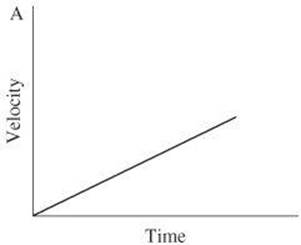
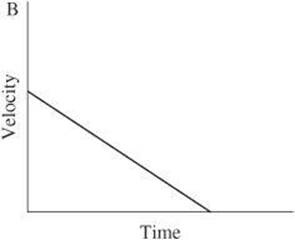
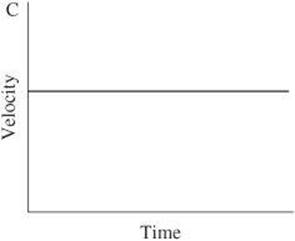
Which of the graphs represent(s) the motion of an object with only balanced forces acting on it?

(A) A only

(B) B only

(C) C only

(D) A and B only

(E) A, B, and C

7. A wagon is accelerating at a rate of 3 m/s². If the net force on the wagon is doubled and the mass is tripled, the acceleration becomes

(A) ½ m/s²

(B) 1 m/s²

(C) 3/2 m/s²

(D) 2 m/s²

(E) 6 m/s²

8. A student on a skateboard pushes against the ground with her foot. The reaction force is exerted

(A) on the ground by the skateboard

(B) on the air by the skateboard

(C) on the ground by her foot

(D) on the skateboard by her foot

(E) on her foot by the ground

Questions 9 and 10 relate to the graph below, which shows the net force F in newtons exerted on a 6-kilogram block as a function of time in t seconds. Assume the block is at rest at t = 0 and that F acts in a fixed direction.

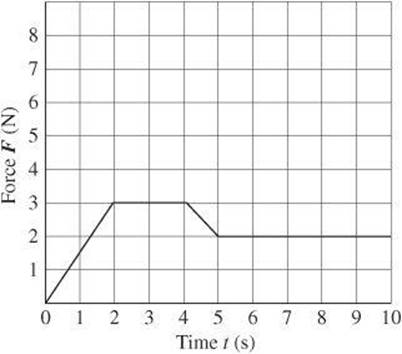
9. Which conclusion can be reached about the motion of the block during the time interval 2 to 4 seconds?

(A) The block is not in motion.

(B) The block is moving with constant acceleration.

(C) The mass of the block is increasing.

(D) The block is moving with constant speed.

(E) The force exerted on the block is decreasing.

10. The acceleration of the block at sec is

(A) 1/3 m/s²

(B) 2 m/s²

(C) 3 m/s²

(D) 6 m/s²

(E) 12 m/s²

QUESTION ANSWERS AND EXPLANATIONS

1. C The net force is zero when the forces in all directions cancel out. Because the forces are exerted in the vertical and horizontal directions only, they can be directly added. Remember to assign a negative to one of the forces in each direction. Add the horizontal forces first, and then the vertical forces. Only in choice C do the forces in both directions add to zero.

2. D The normal is equal in magnitude and opposite in direction to the net downward force on the box. The net downward force is the weight of the box, 32 N, plus the additional downward force, 20 N, which is 52 N.

3. C The weight of an object is the product of its mass and the acceleration due to gravity, which on Earth is approximately 9.8 m/s². Therefore, the mass equals .

4. B According to Newton’s second law of motion, force is directly proportional to acceleration. Therefore, if force is doubled for a constant mass, acceleration is also doubled.

5. A The horizontal forces are balanced, so they cancel. The vertical forces are unbalanced. The net force is the difference between them, 30 N, in the direction of the greater force, southward.

6. C If all the forces acting on an object are balanced, the net force is zero. When the net force is zero, the velocity of an object remains the same. This is true only for the object represented in graph C. The object in graph A is speeding up and the object in graph B is slowing down. Therefore, both objects are accelerating and must have a net force acting on them as the result of unbalanced forces.

7. D If the net force is doubled, the acceleration is also doubled because these quantities are directly proportional. If this change alone occurred, the new acceleration would become 6 m/s². However, the mass is tripled. Because mass and acceleration are inversely related, the acceleration must be divided by this value. So the final acceleration becomes 2 m/s².

8. E According to Newton’s third law of motion, the action and reaction forces are exerted by objects in contact with one another. Therefore, the foot exerts an action force on the ground and the ground exerts a reaction force back on the foot that is equal in magnitude but opposite in direction.

9. B The force and mass on the block during this time interval are constant. Therefore, the acceleration is also constant. The block is in motion and its speed is increasing at a constant rate.

10. A At sec, the force on the block is 2 newtons. According to Newton’s second law of motion, . Therefore, , so a .