WORK, ENERGY, AND POWER - PHYSICS TOPIC REVIEW

SAT Subject Test Physics (2012)

PART III. PHYSICS TOPIC REVIEW

Chapter 5. WORK, ENERGY, AND POWER

The understanding of forces and motion you have developed thus far will enable you to master the concepts of work, energy, and power. Each of the concepts is distinct, yet closely related to the others. Recognizing the meaning of each term in physics, the relationships among them, and how to perform calculations involving them will enable you to solve several different types of questions on SAT Physics.

WHAT IS WORK?

A small child lifting a piece of apple to her mouth does more work than a large weightlifter holding a heavy barbell over his head. Why? Unlike the colloquial definitions of work, scientists have a very specific definition of work. In physics, work is done only when a force exerted on an object causes that object to move some distance. Even if a force is exerted, work is not done if the force does not cause an object to move.

CALCULATING WORK

Work is equal to the product of the force and the displacement of the object in the direction of the force.

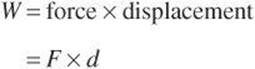
A common SI unit of work is the newton-meter, which is also known as the joule (J). To calculate the work done on or by an object, multiply the force by the displacement the force causes the object to move. If the force is exerted parallel to the direction of movement, multiplication is straightforward.

Example:

A 30-newton force moves a 20-newton object 4 meters. How much work is done by the force?

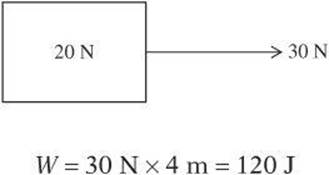
If the force is exerted at angle to the direction of movement, you must first find the component of the force that is parallel to the movement. In this case,

where θ is angle between the force vector and the displacement vector. Actually, you use the same equation to calculate work when the force is parallel to the displacement. In these situations, θ is 0 so the cos 0 is 1. You will not need to perform calculations that require a calculator on SAT Physics, but you may need to use given information to solve a problem.

Example:

A 100-newton force is exerted an angle to move a box a horizontal distance of 8 m as shown.

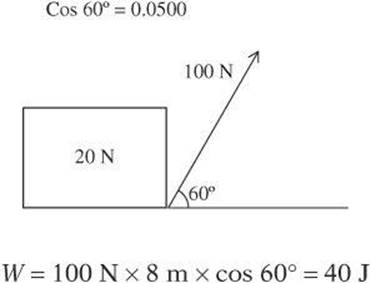
In some situations, the force acts directly opposite to the direction of motion in order to slow it down. The force, therefore, does not cause displacement but instead hinders it. These situations involve negative work because the value of work yields a negative number. The reason is that θ is 180° and cos 180° is -1.

What Is Energy?

The simplest definition of energy in physics is the ability to do work. The units of energy, therefore, are the same as the units of work—joules. There are two general types of energy: potential energy and kinetic energy.

Potential Energy An object has potential energy (PE) due to its position or condition. Because of potential energy, an object has the ability (or potential) to do work. When you lift a book from the floor to your desk, for example, you do work against the force of gravity. Once you lift the book, it has a greater ability to do work. This increase in its ability to do work is its potential energy when compared with its original position on the floor.

The type of potential energy associated with an object that is raised is known as gravitational potential energy (GPE). GPE equals the product of the weight of the object (w) and the vertical height (h) through which it is raised. [Note that gravitational potential energy can also represented as PE_grav or by U_g.]

Example:

An object with a mass of 20 kg is raised 5.0 m. What is its gravitational potential energy?

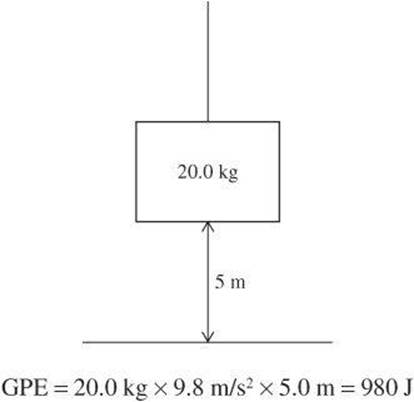
Another form of potential commonly tested on SAT Physics is elastic potential energy, which is energy stored when an elastic material is stretched or compressed. A compressed spring or a stretched rubber band have elastic potential energy. The amount of potential energy is equal to the work done in compressing or stretching.

Some questions on SAT Physics may involve special cases of springs that obey Hooke’s Law. According to Hooke’s Law, a spring exerts a force on a mass attached to it according to the following equation.

where k is a constant of proportionality called the spring constant and x is the displacement from equilibrium. The spring constant varies with the spring. A very tight spring, for example, will have a greater spring constant than a looser spring. You can see from the equation that the further a spring is displaced from equilibrium, the greater the force will be that the spring exerts in the direction of the equilibrium position.

If the potential energy is assigned a value of zero at the equilibrium position, the following equation below can be used to relate the elastic potential energy to the spring constant and the displacement.

Kinetic Energy The energy associated with the motion of a moving body is known as kinetic energy. A rocket traveling through space, a firefly traveling from one leaf to another, and an atom within a sample of matter all have kinetic energy because they are in motion.

There are different types of kinetic energy, including vibrational (objects moving back and forth), rotational (objects turning on an axis), and translational (objects moving from one place to another.) The type of kinetic energy you will encounter most often is translational. This type of kinetic energy is directly proportional to the mass of an object and the square of its velocity according to the following equation.

Example:

A pitcher throws a baseball at 35 m/s. If the baseball has a mass of 0.152 kg, what is the kinetic energy of the ball?

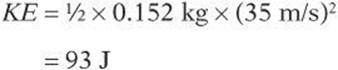
You saw that the potential energy of an object was equal to the work done on it. How is kinetic energy related to work? According to the Work-Energy Theorem, the net work done on an object is equal to the object’s change in kinetic energy.

Mechanical Energy

Both potential energy and kinetic energy are forms of mechanical energy, which is energy acquired by objects upon which work is done. Any object that possesses mechanical energy has the ability to do work. Suppose, for example, you lift a hammer to some height. That hammer has potential energy. If you let the hammer fall, it can exert a force on a nail that causes the nail to move some distance. In other words, the hammer can do work because of its position. Similarly, suppose a billiard ball moving across the table hits into another billiard ball. The first ball can exert a force on the second ball to cause it to move some distance. It does work because of its motion.

The total mechanical energy (TME) of an object is the sum of its kinetic energy and its potential energy.

Other Forms of Energy

In addition to mechanical energy, you will encounter other forms of energy throughout SAT Physics. They will be discussed in context; however, this summary gives you an idea of some of the different forms of energy that exist.

Conservation of Energy

A ball thrown into the air has kinetic energy because of its motion. It also has gravitational potential energy because work has been done to change its height. At no time is any of the ball’s energy destroyed or new energy created. According to the law of conservation of energy, energy can change from one form to another, but it cannot be created or destroyed.

In more advanced topics of physics, it can be shown that mass can be considered a form of energy. Einstein’s theory of relativity leads to the famous equation that relates energy to mass and the speed of light c.

Power

Another important quantity related to work is power, P, which is the rate at which work is done or energy is transformed.

The unit of power is the watt, which is equal to 1 joule per second. If you rewrite the power equation as follows, you can see how power related to both force and speed. A powerful machine, for example, is both strong and fast.

Example:

A person with a mass of 84.2 kg runs up a flight of stairs that has a total height of 5.1 meters. What power is required for the person to run up the stairs in 10.0 seconds, 20.0 seconds, 60.0 seconds?

Notice how the amount of power decreases as the amount of time increases.

Test-Taking Hint

While studying for SAT Physics, make a list or prepare individual index cards relating different units of measurement. For example, know that . Recognizing relationships between units will help you check your work and decide if an answer is reasonable.

REVIEW QUESTIONS

Select the choice that best answers the question or completes the statement.

1. A 15-N horizontal force is applied to push a block across a flat, frictionless surface. If the force causes the block to have a displacement of 4.0 m, how much work is done by the force?

(A) 0 J

(B) 19 J

(D) 54 J

(E) 60 J

2. At which point is the net force acting upward on the mass greatest?

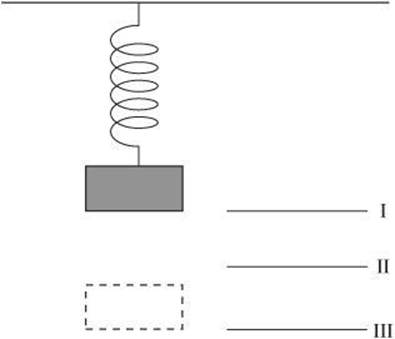
(A) I

(B) between I and II

(D) between II and III

(E) III

3. An 18-kilogram object has an initial kinetic energy of 36 joules. How far will the object move against a net resisting force of 9 newtons?

(A) 2 m

(B) 4 m

(D) 9 m

(E) 30 m

4. A ball with a mass of 0.5 kg moves at a velocity of 10.0 m/s. What is its kinetic energy?

(A) 11 J

(B) 15 J

(D) 35 J

(E) 49 J

5. A cart is pulled at constant speed to the top of an inclined plane. If the mass of the cart is 4.00 kg and the height to which the cart is lifted is 0.52 m, what is the potential energy of the cart at the top of the inclined plane?

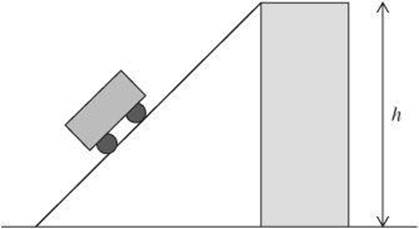
(A) 2.1 J

(B) 9.8 J

(D) 14.3 J

(E) 20.4 J

6. If the velocity of an object is doubled, its kinetic energy is

(A) halved

(B) doubled

(D) quadrupled

(E) unchanged

7. A person with a weight of 340 newtons runs up a flight of stairs to a height of 4.0 meters in 8.0 seconds. The power required for this activity is

(A) 11 W

(B) 43 W

(D) 170 W

(E) 680 W

8. A hydraulic ladder lifts a 100.0-newton box to a height of 3.0 meters in 15 seconds. After the box is lifted, how much power is required to hold the box at that height for 60.0 seconds?

(A) 0 W

(B) 5 W

(D) 20 W

(E) 33 W

Questions 9 and 10 relate to the diagram below, which shows the path of a heavy ball thrown in the air. The ground is level and the dashed lines are parallel to the ground. Assume that frictional forces are negligible.

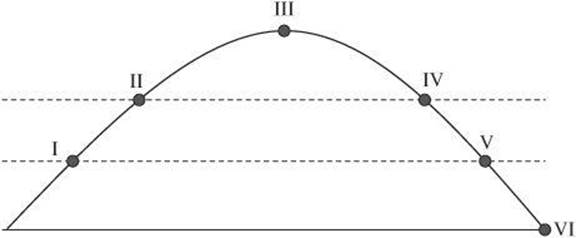
9. The kinetic energy of the ball is least at point

(A) II

(B) III

(D) V

(E) VI

10. At which pair of points is the potential energy of the ball the same?

(A) I and VI

(B) I and II

(D) II and IV

(E) I and III

QUESTION ANSWERS AND EXPLANATIONS

1. E The force is parallel to the displacement, so θ is 0 and cos 0 is 1. Therefore, .

2. E The force exerted on the mass is directly proportional to its displacement from equilibrium. Therefore, the force is greatest at the greatest distance from rest.

3. B The kinetic energy of the object is equal to the work it can do. Therefore, , so .

4. C Translational kinetic equals one-half the mass of the ball times the square of its velocity. So .

5. E The potential energy at the top of the inclined plane is mgh, so .

6. D Kinetic energy is directly related to the square of the velocity. If the velocity is doubled, the kinetic energy is then multiplied by a factor of 4 .

7. D The work the person does to climb the stairs is force (weight) times distance. Power is the work done divided by the time during which the work is done. Therefore,

8. A Power is the rate at which work is done. Work is only done when a force causes an object to move some distance. If the box is being held in one position, work is not done, so no power is involved.

9. B As the ball rises, the potential energy decreases, and the kinetic energy decreases. At the point where the ball reaches the peak of the curve, it stops moving and changes direction. At this point, kinetic energy is zero.

10. D The gravitational potential energy of the ball depends on its height. Therefore, the GPE is the same at points I and V, as well as at points II and IV.