SAT Subject Test Physics (2012)
PART III. PHYSICS TOPIC REVIEW
Chapter 7. LINEAR MOMENTUM
In everyday usage, the word momentum is commonly used to describe objects in motion. You might say that a car has momentum, an athlete has momentum, or even a team has momentum. In other words, the objects are in motion and are difficult to stop. The scientific use of the term is not all that different. For SAT Physics, you will need to understand the scientific definition of the term and how to perform any calculations related to it.
Momentum
The linear momentum, or simply momentum, of an object is the product of its mass and velocity. Momentum is generally represent by p, which makes the equation for momentum
![]()
Mass is a scalar quantity, and velocity is a vector quantity, which makes momentum a vector quantity. Momentum is in the same direction as the velocity of the object. Common units of momentum are kg · m/s.
An object can have considerable momentum if it has either great mass or velocity. A train can have great momentum because of its great mass, even if it is traveling very slowly. A bullet can have great momentum because of its high velocity, even though its mass is very small. Two objects with different masses can have the same momentum depending on their velocities. An object at rest has no momentum.
Example:
A ball with a mass of 2.0 kg is traveling with a velocity of 4.0 m/s west. What is the ball’s momentum? By how much does the momentum change if the velocity is doubled?

When the velocity is doubled, the momentum is also doubled.
Impulse
Unlike momentum, the everyday use of the word impulse is different from its scientific use. The scientific definition of impulse derives from Newton’s Second Law. Recall from Chapter 4 that this law states that a net force will cause an object to accelerate, and the amount of acceleration depends on the magnitude of the force and the mass of the object. The equation for Newton’s Second Law can be rearranged to relate it to momentum.
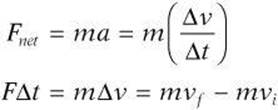
The left side of the equation (FΔt) is defined as the impulse. It is equal to the change in momentum (mΔv). Impulse is a vector quantity. The unit of impulse is the same as the unit of momentum. The equation is sometimes known as the impulse-momentum theorem, which states that the force acting on a mass during a given time interval changes the momentum of the mass.
Example:
Find the applied force that causes a 10 m/s change in the velocity of the box in 5 s if the mass of the box is 5 kg.
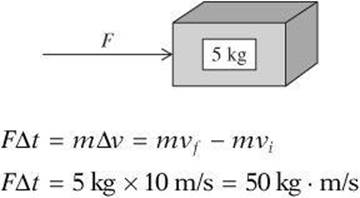
The impulse is 50 kg · m/s.
![]()
SAT Physics often uses graphs to test your understanding of momentum. The impulse caused by a force exerted on an object during a time interval equals the area under the force versus time graph during that time interval.
Example:
Consider the following graph.
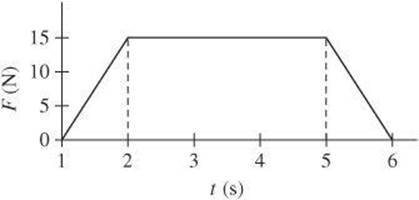
(A) What is the impulse acting on the object between 2.0 s and 5.0 s?
(B) What is the change in momentum between 2.0 s and 5.0 s?
(A) The impulse during the time interval is the area under the graph during that interval.
![]()
(B) The change in momentum equals the impulse, so the change in momentum is also 45 N s.
Conservation of Momentum
If a force acts on an object, the momentum of the object changes. If there is no unbalanced force acting on an object, the total momentum of the system must remain constant. In other words, momentum is conserved. SAT Physics may test your understanding of conservation of momentum in different ways, including inelastic collisions and elastic collisions.
Inelastic Collisions An inelastic collision occurs when two objects crash and become stuck together, either completely or partially. For example, suppose two train cars on a track collide such that one hooks onto the other. Momentum is conserved, but kinetic energy is not.
Example:
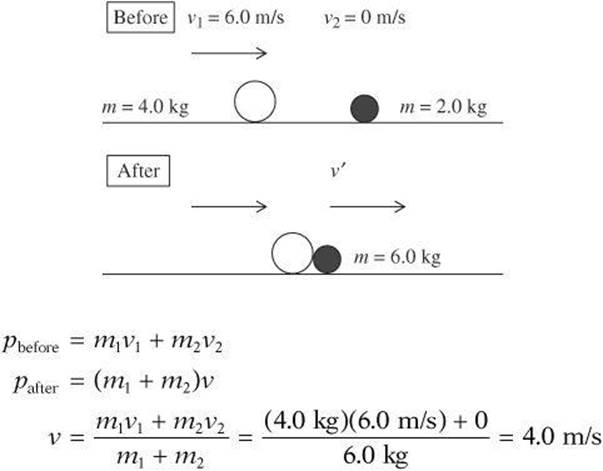
A ball with a mass of 4.0 kg is moving to the right with a velocity of 6.0 m/s collides with a 2.0 kg ball at rest. Upon collision, the balls stick together. What is the velocity immediately after the collision?
Elastic Collisions An elastic collision occurs when two objects crash but do not stick together. Instead, they bounce off each other. For example, two billiard balls may collide and bounce off in opposite directions. Both momentum and kinetic energy are conserved in this type of collision.
Example:
A white billiard ball with a mass of 0.5 kg is moving at 8 m/s. It collides with a black billiard ball with the same mass that is at rest. After the collision, the white ball continues in the same direction with a velocity of 2.2 m/s. If you ignore friction, what is the velocity of the black ball?
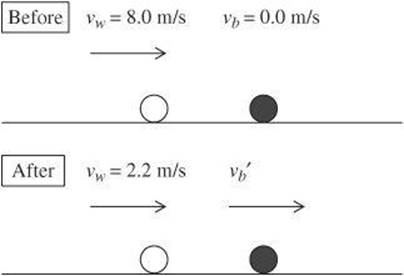
momentum before collision = momentum after collision
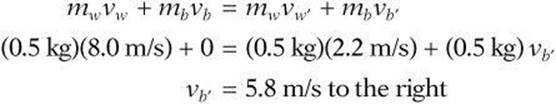
Center of Mass
When considering collisions, the mass was assumed to be concentrated in a single point known as the center of mass. Using the center of mass is convenient because it enables you to treat an object as a point mass, so that you can ignore the overall shape of the object or system. The center of mass is not always within the object itself.

More specifically, it may be helpful for you to understand how to calculate the center of mass for a collection of particles. For two particles separated by a distance d, the center of mass xcm is found as follows.
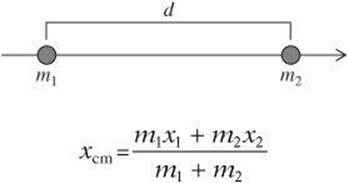
Test-Taking Hint
Pay attention to conventions for directions when it comes to velocity and momentum. By convention, movement to the right is generally described by positive values, whereas movement to the left is generally described by negative values.
REVIEW QUESTIONS
Select the choice that best answers the question or completes the statement.
1. A ball with a mass of 0.1 kg is traveling at 5 m/s from right to left. What is the momentum of the ball?
![]() to the left
to the left
![]() to the left
to the left
![]() to the right
to the right
![]() to the left
to the left
![]() to the right
to the right
2. A 70-kg runner is traveling from left to right. If the runner has a momentum of 560 kg · m/s to the right, what is the runner’s velocity?
(A) 4.9 m/s to the right
(B) 5.6 m/s to the left
(C) 7.5 m/s to the left
(D) 8.0 m/s to the right
(E) 12.6 m/s to the right
3. A baseball player bunts a ball by holding the bat loosely. The momentum of the bat before the collision is 80 units. The momentum of the ball is -40 units before the collision and 10 units after the collision. What is the momentum of the bat after the collision?
(A) 10 units
(B) 20 units
(C) 30 units
(D) 60 units
(E) 70 units
4. Two balls are moving directly toward one another. One has a mass of 4.0 kg and is moving to the right with a velocity of 6.0 m/s. The other has a mass of 2.0 kg and is moving toward the left with a velocity of 4.0 m/s. They collide inelastically. What is the speed of the combined balls immediately after the collision?
(A) 1.8 m/s
(B) 2.0 m/s
(C) 2.7 m/s
(D) 5.3 m/s
(E) 12.0 m/s
5. A force of 10 N acts on a 2-kg object for 3 seconds. What is the change in the speed of the object?
(A) 7.5 m/s
(B) 15 m/s
(C) 30 m/s
(D) 45 m/s
(E) 60 m/s
6. Railroad car A travels from left to right at 20 m/s, while railroad car B travels from right to left at 20 m/s. The cars couple together upon collision. What is their combined velocity?
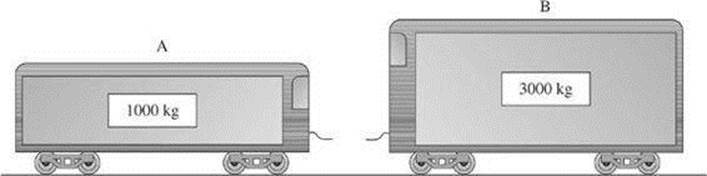
(A) 10 m/s to the left
(B) 10 m/s to the right
(C) 14 m/s to the left
(D) 14 m/s to the right
(E) 40 m/s to the left
7. A cannon with a mass of 500 kg fires a cannon ball with a mass of 5 kg. The cannon ball travels with an initial velocity of 150 m/s to the right. The cannon moves backward, or recoils, as the ball is shot. What is the magnitude of the recoil velocity of the cannon ball?
(A) 0.67 m/s
(B) 1.5 m/s
(C) 3.3 m/s
(D) 7.5 m/s
(E) 30 m/s
8. A bullet with a mass of 0.020 kg collides with a block of wood with a mass of 3.2 kg. The block of wood is initially at rest. If the bullet and block combination move with a speed of 1.1 m/s after the collision, what was the initial speed of the bullet?
(A) 32 m/s
(B) 62 m/s
(C) 80 m/s
(D) 140 m/s
(E) 180 m/s
Questions 9 and 10 relate to the diagram below, which shows a force vs time graph for an object.
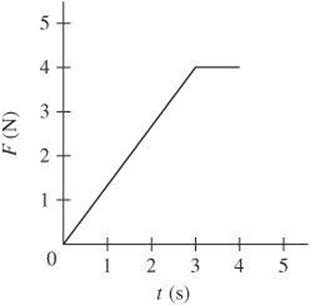
9. What is the impulse delivered by the force graphed in the graph between t = 0 and ![]() ?
?
(A) 4 kg · m/s
(B) 10 kg · m/s
(C) 12 kg · m/s
(D) 16 kg · m/s
(E) 20 kg · m/s
10. If the mass of the object is 10 kg and it has a velocity of 4 m/s at 3 s, what is its velocity at 4 s?
(A) 3.6 m/s
(B) 4.4 m/s
(C) 6.0 m/s
(D) 9.6 m/s
(E) 14 m/s
QUESTION ANSWERS AND EXPLANATIONS
1. ![]() to the left
to the left
2. ![]() , so
, so ![]()
![]() to the right
to the right
3. C The total momentum before and after the collision must be the same. The total momentum before the collision is 40 units, so it must be 40 units (30 units + 10 units) after the collision.
4.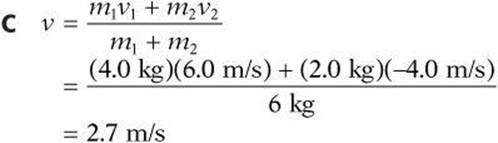
5. B The change in momentum is equal to the impulse.
![]() in the direction of the force
in the direction of the force
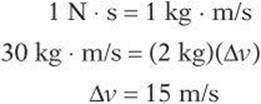
6. A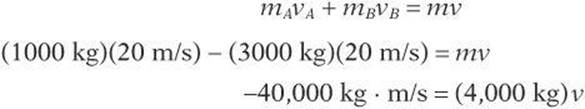
![]() , which indicates that the direction is to the left
, which indicates that the direction is to the left
7. B The original momentum of the combination of cannon and cannon ball is 0 kg · m/s, so the final momentum must also be 0 kg · m/s. Make the velocity of the cannon ball positive and the velocity of the cannon negative. Therefore,
momentum of the cannon ball + momentum of the ![]()
![]()
![]() to the left
to the left
8.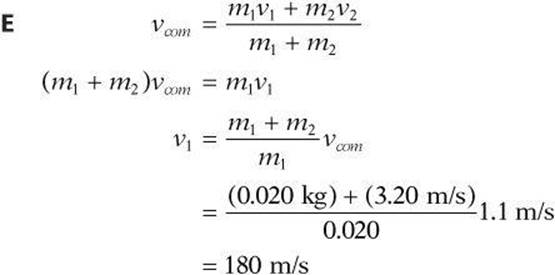
9. B The impulse equals the area of a triangle of height 4 and base 3 plus the area of the rectangle with height 4 and base 1.
![]()
10. B According to the Impulse-Momentum Theorem,
![]()
The impulse during that time interval is 4 N · s.
