SAT Subject Test Physics (2012)
PART III. PHYSICS TOPIC REVIEW
Chapter 8. CIRCULAR AND ROTATIONAL MOTION
So far, you have been investigating linear motion, which is motion in a straight line. Many examples of motion, however, are not linear. In this chapter, you will investigate circular and rotational motion. SAT Physics may ask both qualitative and quantitative questions involving these topics.
Uniform Circular Motion
An object is said to move in uniform circular motion if it moves at a constant speed in a circle. The speed of the object is constant, but the velocity is constantly changing because the direction is constantly changing. In addition to velocity, two other vectors are associated with uniform circular motion—centripetal force and centripetal acceleration.
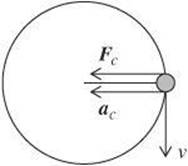
The word centripetal means “center seeking.” The centripetal force (Fc) acts on the object toward the center of the circle. This force does not change the speed of the object. Instead, it constantly accelerates the object toward the center of the circle, which is why it changes direction.
The resulting acceleration, the centripetal acceleration (ac), depends on the velocity of the object and the radius of the circle.
The magnitude of centripetal acceleration remains constant, but the direction is constantly changing. The direction is always toward the center of the circle, which must change as the object moves around its circular path. Centripetal acceleration is in the same direction as the centripetal force and perpendicular to the velocity.
According to Newton’s Second Law, the net force equals the product of mass and acceleration.
The period (T) of an object in uniform circular motion is the time it takes to complete on revolution. Period is measured in a unit of time, such as seconds or minutes. The number of revolutions per unit time is the frequency (f) of the object. Frequency is measured in revolutions per unit of time, such as revolutions per second or revolutions per minute. The unit revolutions per second is also known as the hertz.
Speed equals distance divided by time. For an object in uniform circular motion, the distance is the circumference of the circle and the time is the period.
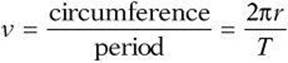
Example:
A ball with a mass of 3.0 kg is swung in a circular path at the end of a rope with length 2.0 m. If the speed of the ball is 1.0 m/s, what is the tension on the rope? Assume the rope to be massless.
The tension on the rope is equal to the centripetal force.
Rotational Motion
If you think of a circle as a straight line that has been rolled up, it makes sense that the quantities you apply to straight-line motion can be used to analyze rotational motion. The rotational components are described as angular—angular displacement (θ), angular velocity (ω), and angular acceleration (α).
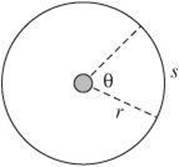
If the disk in the diagram rotates such that the arc length (s) equals the radius (r), the subtended angle, which is the angular displacement θ, will equal 1 radian.
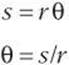
If the disk rotates one complete revolution, s becomes equal to the circumference. This means that 
radians and 2π 
.
Although you will not be required to do so on SAT Physics, it will help you to understand how to derive the next relationships. By differentiating the equation s = r θ, you find the relationship for angular velocity.
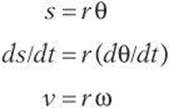
Thus, angular velocity 
. The unit of angular velocity is radians per second.
Differentiating again gives the angular acceleration.
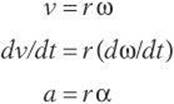
Thus, angular acceleration 
. The unit of angular acceleration is radians per second squared.
You can see that each angular component is related to r, the distance to the center of the circle. When velocity is constant, 
becomes 
.
Example:
What is the angular velocity of the second hand of a clock?
Torque
With the basics of rotational kinematics mastered, you can comfortably approach questions involving rotational dynamics, such as torque. Essentially, torque is a measure of how much a force acting on an object causes that object to rotate. The force must be applied to any point other than the center of mass. A net force applied to an object’s center of mass will not result in rotation.
More formally, torque (τ) is the product of the component of the force perpendicular to the radius (F⊥) and the radius (r).
Torque is a vector quantity measured in newton-meters (N · m).
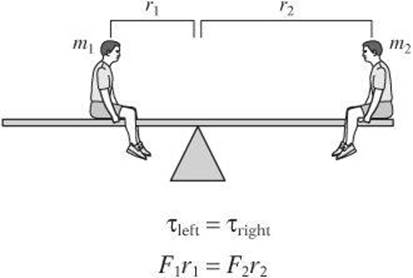
Consider the massless lever in the following diagram.
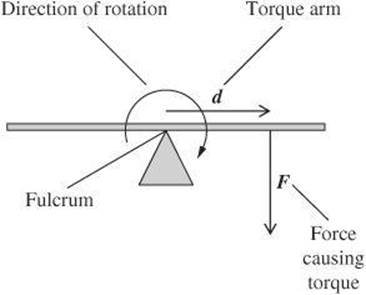
The force exerted on one end of the board causes the board to rotate in the direction indicated by the curved arrow. The distance between the point of rotation and the fulcrum, identified by d, is known as the torque arm. If the torque arm is 3.0 m long and the force is 4.0 N, the magnitude of the torque is calculated as follows.
Torque associated with clockwise rotation is considered to be directed into the page, whereas counterclockwise torque is directed out of the page. You can use the right-hand rule to identify direction. Wrap the fingers of your right hand in the direction of rotation caused by the force. Your thumb will point in the direction of the torque vector.
In the preceding example, the force was exerted at a right angle to the torque arm. This made the calculation ordinary multiplication. If the angle is not a right angle, the calculation must account for the angle made between the force vector and the lever. Consider the lever attached to the wall as shown in the following diagram.
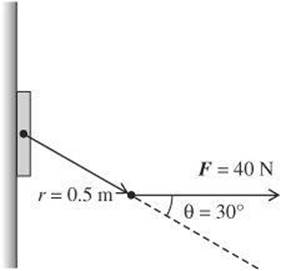
Suppose a force of 40 N is exerted on the lever 0.5 m from its axis of rotation. The force forms an angle of 30° with the lever arm. What is the torque on the lever arm?
If a system is at equilibrium, both the sum of the forces and the sum of the torques must equal zero. If the net torque is zero and the object is not rotating, the object will not begin rotating.
Example:
Two people are on either end of a seesaw. One person has a mass of 
kg and the other person has a mass of 
. The seesaw is 8 m long and pivoted on an axis at its center. At what distance from the axis must the first person sit to keep the seesaw horizontal?
The force is applied perpendicular to the seesaw by gravity.
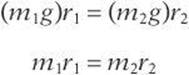
to the left of the axis
Angular Momentum
Just as you found linear momentum for objects moving in a straight line, you can find angular momentum for objects moving in curved paths. Angular momentum (L) for a circular orbit is defined at the product of mass, velocity, and radius of orbit.
You will revisit the topic of angular momentum in Chapter 9, but for now it would be helpful for you to become familiar with the general concept. Recognize that angular momentum is conserved if there are no external torques on an object. Therefore, if the radius of an orbit is decreased, the speed will decrease. This explains why ice skaters spin faster when they tuck their bodies in more tightly.
Test-Taking Hint
Many linear and rotational equations are related. Make a list relating equations so you can study them together. If you become confused by a test question, you may be able to recall the equation you need by remembering the related equation.
REVIEW QUESTIONS
Select the choice that best answers the question or completes the statement.
1. A ball is swung around at the end of a string in a horizontal circle rotating counterclockwise as shown. The string breaks when the ball is in the position shown. In which direction will the ball move?
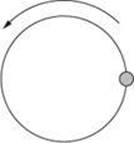
(A) up and to the left
(B) down and to the left
(C) to the top of the page
(D) to the right
(E) to the left
2. A car with a mass of 800 kg moving at 12 m/s turns around a circle with a radius of 30.0 m. What is the magnitude of the acceleration of the car?
(A) 4.0 m/s2
(B) 4.8 m/s2
(C) 5.5 m/s2
(D) 9.0 m/s2
(E) 11.3 m/s2
3. A 60-kg student goes on a ride at an amusement park that spins quickly. Then the floor drops out. If the ride has a radius of 2.5 m and makes 10 revolutions in 32.3 s, what is the centripetal force acting on the student?
(A) 155 N
(B) 194 N
(C) 323 N
(D) 486 N
(E) 567 N
4. A 2-kg ball is spun on the end of a string in a circle with a radius of 8.0 m. If the maximum tension on the string is 40 N, what is the maximum speed of the ball?
(A) 2.0 m/s
(B) 3.16 m/s
(C) 12.6 m/s
(D) 14.9 m/s
(E) 16.0 m/s
5. A grooved wheel turning at 800 rev/min has a diameter of 6 cm. As it turns, a wire is wound onto it. How long a piece of wire will be wrapped in 10 seconds?
(A) 2.4 m
(B) 5.9 m
(C) 24.0 m
(D) 25.2 m
(E) 80.0 m
6. The diagram below shows two masses balanced on a scale. What is m2 in terms of m1 if the bar of the scale is horizontal and massless?
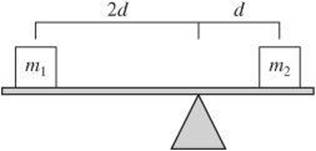
(A) 1/2m1
(B) 2m1
(C) m1
(D) m12
(E) 4m1
7. The angular velocity of the tires on a car increase from 32 rad/s to 50 rad/s in 1.45 s. What is the angular acceleration of the tires?
(A) 5.66 rad/s2
(B) 12.41 rad/s2
(C) 16.6 rad/s2
(D) 18.0 rad/s2
(E) 26.1 rad/s2
8. A meteorologist is studying a tornado, which is spinning counterclockwise to the plane of the ground. In which direction does the angular velocity vector point?
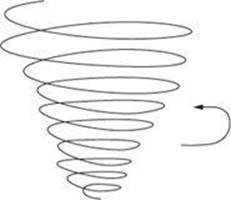
(A) upward to space
(B) downward toward the ground
(C) toward the right
(D) toward the left
(E) into the center of the tornado
Questions 9 and 10 relate to the diagram below, which shows a mass swinging at the end of a string at 2.0 m/s.
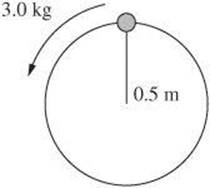
9. What is the centripetal acceleration of the object?
(A) 2.0 m/s2
(B) 2.5 m/s2
(C) 4.0 m/s2
(D) 8.0 m/s2
(E) 10.0 m/s2
10. What is the centripetal force on the object?
(A) 8.0 J
(B) 16 J
(C) 24.0 J
(D) 28 J
(E) 32 J
QUESTION ANSWERS AND EXPLANATIONS
1. C The ball is moving to the top of the page when the string breaks. It would continue to move in that direction.
2. B Use the equation for centripetal acceleration: 
.
3. E Because it takes 32.3 s to complete 10 revolutions, 
. Find speed as 
. Find acceleration as 
. Finally, find force as 
.
4. 
, so
5. D The angular equations show that 
and 
. Substituting one into the other gives 
. Using the information provided, 
.
6. B The torque on each side of the axis must be equal.
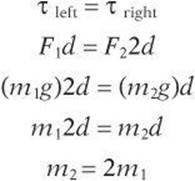
7. B Angular acceleration α equals the change in angular velocity divided by time.
8. A Use the right-hand rule to bend your fingers in the direction of the tornado’s spin. Your thumb, which points upward, shows the direction of the angular velocity vector.
9. D Use the equation for centripetal acceleration: 
.
10. C Use the force equation: 
.