SAT Subject Test Physics (2012)
PART III. PHYSICS TOPIC REVIEW
Chapter 9. GRAVITY
The reason you are able to sit in a chair as you read these words is because of gravity. This force not only holds you and other objects on Earth’s surface but also holds the solar system together. SAT Physics will present you with several types of questions involving gravity. While some questions may involve direct calculations, the majority will test your understanding of relationships among quantities and the effects of changes on one or more of those quantities.
Newton’s Law of Universal Gravitation
According to Newton’s Law of Universal Gravitation, a force of attraction exists between every pair of masses in the universe. The magnitude of the force is directly proportional to the product of the masses and inversely proportional to the square of the distance between their centers. This relationship is described by the following equation, in which Fg is the gravitational force, m1 and m2 are the masses, and r is the distance between their centers. The constant G, known as the gravitational constant, equals 6.67 × 10–11 N · m2/kg2.
![]()
The SAT Physics test will generally not test your recall of the gravitational constant, but instead ask questions about your understanding about the relationships between the other variables. For example, you should recognize that the gravitational force is a vector quantity. The gravitational force exerted by m1 pulls m2 toward its center, whereas the gravitational force exerted by m2 pulls m1 toward its center. The forces exerted by the masses are equal in magnitude but opposite in direction.
Example:
Two masses m are separated by a distance r are attracted to each other by a gravitational force F.
(A) If the mass of one of the objects is doubled, what will be the new gravitational force in terms of F?
(B) If the mass of both objects is doubled, what will be the new gravitational force in terms of F?
(C) If the distance between the objects is doubled, what will be the new gravitational force in terms of F?
![]() and one of the masses becomes 2m.
and one of the masses becomes 2m.
So, ![]() or 2F.
or 2F.
![]() and both masses become 2m.
and both masses become 2m.
So, ![]() or 4F.
or 4F.
![]() and r becomes 2r.
and r becomes 2r.
So, ![]() or 1/4F.
or 1/4F.
Acceleration Due to Gravity
You often use the value of 9.8 m/s2 to represent the acceleration due to gravity near Earth’s surface. This value can be derived from Newton’s Law of Universal Gravitation. Begin with Newton’s Second Law, F = ma. Then substitute the equation for the gravitational force.
![]() ,
,
which becomes
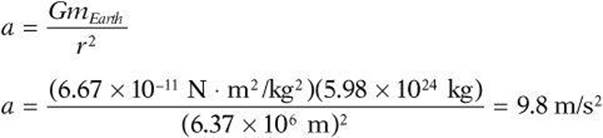
This value is true at or near Earth’s surface. However, if the distance from Earth’s surface increases, the radius will also change. Like the gravitational force, the acceleration due to gravity is also inversely proportional to the distance between the centers of the masses. A distance two Earth radii from the center of Earth would result in an acceleration that is one-fourth the value at the surface.
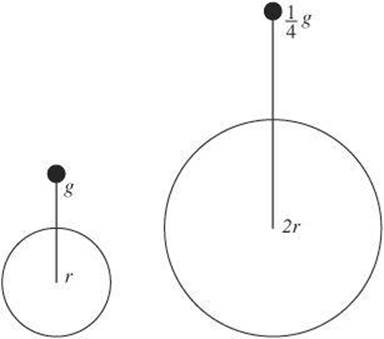
Notice that the mass of the object being pulled by Earth cancels out of the equation. This explains why objects fall to Earth with the same acceleration regardless of mass.
Kepler’s Laws
In the early 1600s, Johannes Kepler formulated three laws of planetary motion. Developed before Newton proposed his laws of motion and universal gravitation, Kepler’s laws were based on observations made by the astronomer Tycho Brahe.
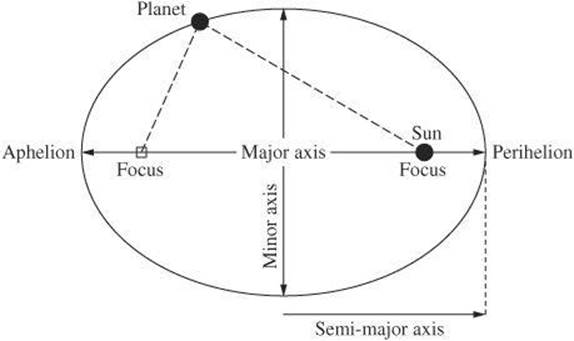
Kepler’s First Law (Law of Ellipses) The shape of each planet’s orbit is an ellipse with the sun at one focus. Although planetary orbits are often approximated as circles, they are actually elliptical in shape.
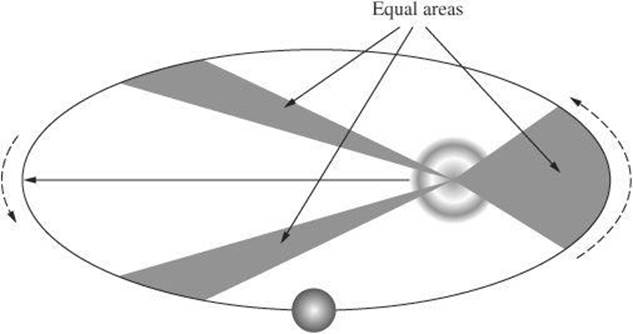
Kepler’s Second Law (Law of Equal Areas) Each planet sweeps out equal areas in equal times. The speed at which a planet moves changes throughout its orbit. The speed increases as the planet moves closer to the sun and decreases as it moves away from the sun. If an imaginary line were drawn between a planet and the sun, the area swept out by the line during any time period would be the same. The following diagram shows areas swept out during equal periods of time.
Kepler’s Third Law (Law of Harmonies) The time it takes for a planet to orbit the sun, its orbital period, is related to its distance from the sun. The ratio of the square of the period to the cube of the semimajor axis, T2/a3, is the same for all planets.
Orbital Speed
To determine the orbital speed of a planet, you need to approximate its path as a circle. The centripetal force acting on the planet is equal to the force of gravity exerting by the sun. You can therefore set the equation for universal gravitation equal to the equation for centripetal force.

Therefore, the orbital speed of a planet depends on the gravitational constant, the mass of the sun, and the planet’s distance to the sun. Now you can see why a planet moves faster when it is closer to the sun (r smaller) slower when it is farther away (r larger).
Test-Taking Hint
Make sure you are comfortable with different types of relationships. For example, quantities that are directly related change together. Both increase or decrease together. Quantities that are indirectly related change in opposite directions. If one increases, the other decreases.
REVIEW QUESTIONS
Select the choice that best answers the question or completes the statement.
1. Two 60-kg students are standing 1 m apart. What is the magnitude of the gravitational force each student exerts on the other? ![]()
(A) 4.00 × 10–9 N
(B) 2.40 × 10–7 N
(C) 3.60 × 10–7 N
(D) 6.67 × 10–4 N
(E) 4.02 × 10–3 N
2. What is the relationship between G and g?
(A) G describes gravity on Earth, whereas g describes gravity in space.
(B) G is a universal constant, whereas g is acceleration due to the gravitational force.
(C) G is the gravitational force, whereas g is gravitational acceleration.
(D) G is the speed of an object due to gravity, whereas g is the acceleration due to gravity
(E) G describes the gravitational force exerted by an object, whereas g describes the gravitational force exerted on an object.
3. The mass of Mars is 6.42 × 1023 kg and its radius is 3.37 × 106 m. What is the ratio of its gravitational acceleration on the surface of Mars to that on the surface of Earth? ![]()
(A) 0.38
(B) 0.65
(C) 0.87
(D) 1.03
(E) 2.60
4. A satellite is orbiting Earth at an altitude that is equal to the radius of the planet. The gravitational force exerted on the satellite by the planet is F. The satellite is then brought down to the Earth’s surface. What is the new gravitational force exerted on the satellite?
(A) F/4
(B) F/2
(C) F + 4
(D) 2F
(E) 4F
5. A satellite orbits the sun as shown in the diagram below. If the satellite travels from A to B during the same period of time as it travels from C to D, which of the following conclusions can be reached?
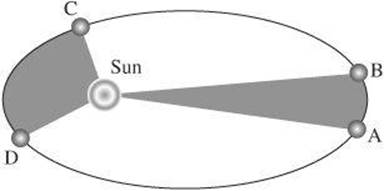
(A) The satellite travels at a greater speed from C to D than from A to B.
(B) The triangle containing A and B covers less area than the triangle containing C and D.
(C) The gravitational force on the satellite is greater between A and B than between C and D.
(D) The mass of the satellite is greater between C and D than between A and B.
(E) The ratio of the period to the average distance to the sun is greater between A and B than between C and D.
6. Earth has a period of 1 year and an average distance to the sun of 1 AU. If the average distance between Saturn and the sun is 9.54 AU, what is Saturn’s period of revolution?
(A) 5.4 years
(B) 9.1 years
(C) 19.1 years
(D) 29.5 years
(E) 57.2 years
7. Two planets A and B orbit a star in elliptical paths. The semimajor axis of planet A has a length l and the semimajor axis of planet B has a length 16l. If planet A orbits with period T, what is the period of planet B’s orbit?
(A) 16T
(B) 24T
(C) 64T
(D) T/4
(E) T/64
8. Each of the following quantities affects Earth’s motion through space.
I. mass of Earth
II. mass of sun
III. distance to sun
Upon which of the quantities does the orbital speed v depend?
(A) I only
(B) I and II only
(C) I and III only
(D) II and III only
(E) I, II, and III
Questions 9 and 10 relate to the diagram below, which shows that two identical masses are separated by a distance r.
![]()
9. How will the gravitational force between the masses be affected if the distance between them is changed to r/2?
(A) It decreases by a factor of 4.
(B) It decreases by a factor of 2.
(C) It increases by a factor of 2.
(D) It increases by a factor of 4.
(E) It increases by a factor of 8.
10. Which of the following will have the same effect on gravitational force as doubling the distance between the masses?
(A) halving both masses
(B) halving one mass
(C) doubling one mass and halving the other
(D) doubling both masses
(E) doubling both masses and dividing the distance between them
QUESTION ANSWERS AND EXPLANATIONS
1.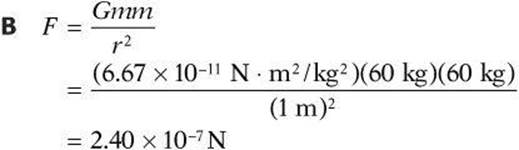
2. B The values G and g are often confused. The quantity represented by G is a universal constant found within the equation describing universal gravitation. The quantity represented by g is the acceleration due to gravity and varies with the magnitude of the gravitational force in a particular location.
3. A Use the acceleration equation to find g:
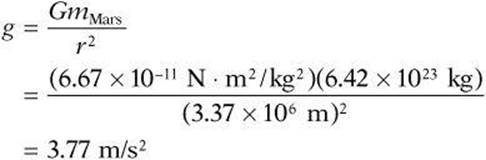
Then compare with g on Earth, which is 9.81 m/s2. So, ![]() .
.
4. E The original force is found as ![]() . The radius is then halved.
. The radius is then halved.
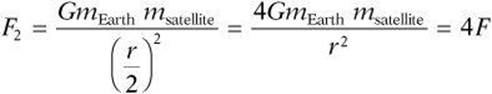
5. A Kepler’s Second Law states that a line connecting a planet to the sun sweeps out equal areas in equal times. The planet therefore must move faster when it is closer to the sun than when it is farther from the sun.
6. D The period is T and the average distance is a as described by Kepler’s Third Law, ![]() . This ratio is the same for all planets.
. This ratio is the same for all planets.
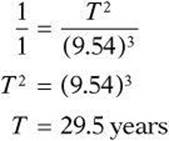
7. C According to Kepler’s Third Law, the ratio T2/a3 is constant. Set the period of planet B equal to xT. Then
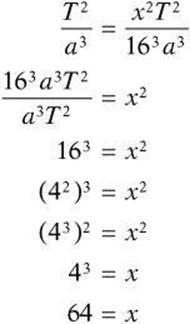
8. D The orbital speed 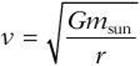 depends on the gravitational constant, the mass of the sun, and the planet’s distance to the sun. The equation does not include the mass of the planet.
depends on the gravitational constant, the mass of the sun, and the planet’s distance to the sun. The equation does not include the mass of the planet.
9. ![]() , so if r becomes r/2,
, so if r becomes r/2, 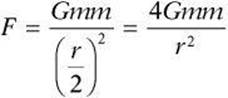 . Therefore, the force is multiplied by 4.
. Therefore, the force is multiplied by 4.
10. ![]() , so if r is doubled,
, so if r is doubled, ![]() , or ¼F.
, or ¼F.
Another way to achieve the same result is to reduce each mass by ½.
![]() , so if both masses are halved,
, so if both masses are halved, 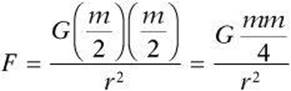 , or ¼F.
, or ¼F.