SAT Test Prep
CHAPTER 7
ESSENTIAL PRE-ALGEBRA SKILLS
Lesson 3: Fractions
Example:
Adding and Subtracting Fractions
Just as 2 apples + 3 apples = 5 apples, so 2 sevenths + 3 sevenths = 5 sevenths! So it”s easy to add fractions if the denominators are the same. But if the denominators are different, just “convert” them so that they are the same.
When “converting” a fraction, always multiply (or divide) the numerator and denominator by the same number.
Example:
![]()
If the denominator of one fraction is a multiple of the other denominator, “convert” only the fraction with the smaller denominator.
Example:
![]()
One easy way to add fractions is with “zip-zap-zup”: cross-multiply for the numerators, and multiply denominators for the new denominator. You may have to simplify as the last step.
Example:
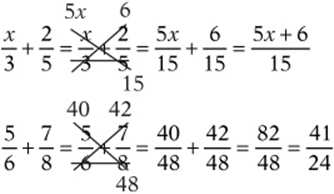
Multiplying and Dividing Fractions
To multiply two fractions, just multiply straight across. Don”t cross-multiply (we”ll discuss that in the next lesson), and don”t worry about getting a common denominator (that”s just for adding and subtracting).
Example:
![]()
To multiply a fraction and an integer, just multiply the integer to the numerator (because an integer such as 5 can be thought of as 5/1).
Example:
![]()
To divide a number by a fraction, remember that dividing by a number is the same as multiplying by its reciprocal. So just “flip” the second fraction and multiply.
Example:
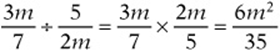
Simplifying Fractions
Always try to simplify complicated-looking fractions. To simplify, just multiply or divide top and bottom by a convenient number or expression. If the numerator and the denominator have a common factor, divide top and bottom by that common factor. If there are fractions within the fraction, multiply top and bottom by the common denominator of the “little” fractions.
Example:
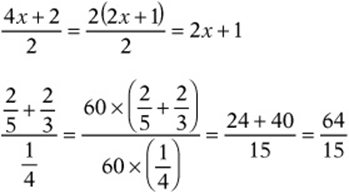
(Notice that, in the second example, 60 is the common multiple of all of the “little denominators”: 5, 3, and 4.)
Be careful when “canceling” in fractions. Don”t “cancel” anything that is not a common factor. To avoid the common canceling mistakes, be sure to factor before canceling.
Example:
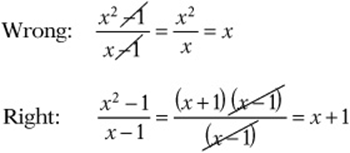
Concept Review 3: Fractions
Simplify the following expressions:
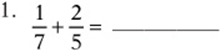
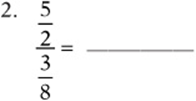
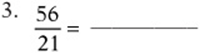
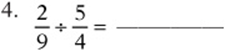
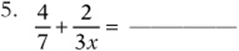
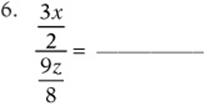
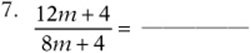
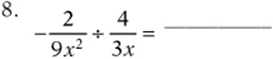
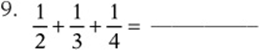
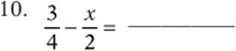
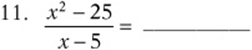
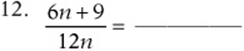
Convert each expression to a fraction:
![]()
![]()
![]()
![]()
17. How do you divide a number by a fraction?
![]()
18. How do you add two fractions by “zip-zap-zup”?
![]()
19. What can be canceled to simplify a fraction?
![]()
20. How do you convert a fraction to a decimal?
![]()
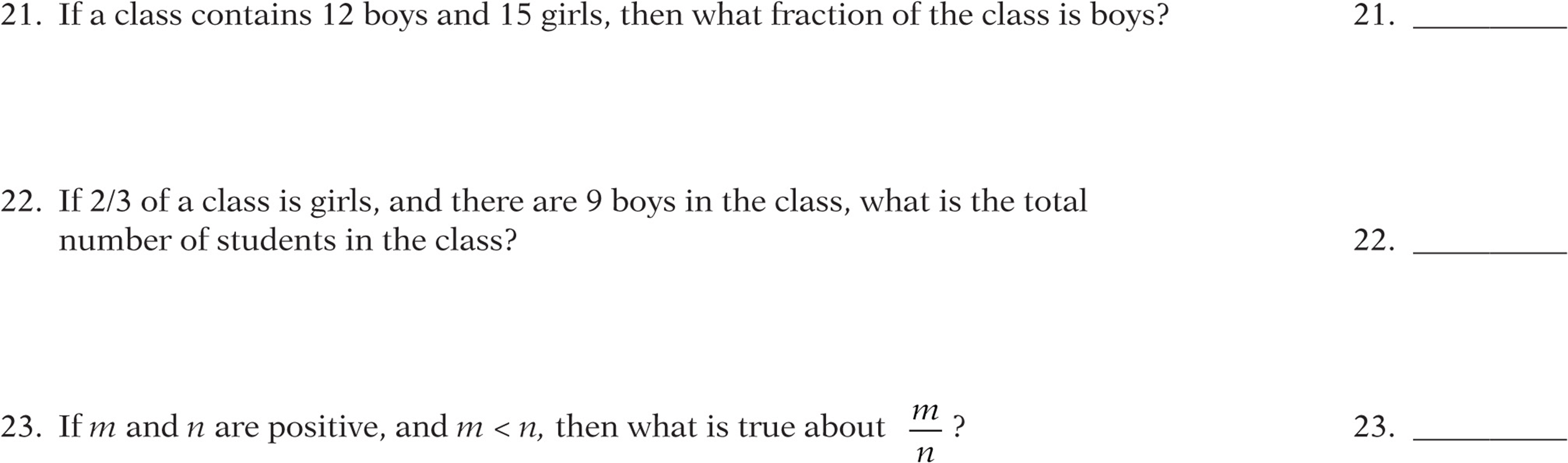
SAT Practice 3: Fractions
1. If 4 quarts of apple juice are mixed with 5 quarts of cranberry juice and 3 quarts of grape juice, what part of the total mixture is apple juice?
![]()
![]()
![]()
![]()
![]()
2. For what value of y does 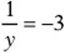 ?
?
(A) –3
![]()
![]()
(D) 3
(E) 6
3. Which of the following is greatest?
![]()
![]()
![]()
![]()
![]()
4. If 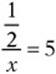 , then x =
, then x =
![]()
![]()
![]()
![]()
(E) 10
5. If ![]() , then
, then ![]()
![]()
![]()
![]()
(D) 3
(E) 5
6. If ![]() and
and ![]() , then
, then ![]()
(A) –1
(B) 0
(C) ½
(D) 1
(E) 2
7. If ![]() , then
, then ![]()
![]()
![]()
(C) 5
(D) 7
(E) 14
8. If ![]() , which of the following is equivalent to
, which of the following is equivalent to 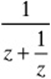 ?
?
(A) 1
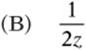
(C)![]()
![]()
![]()
9. Five-eighths of Ms. Talbott”s students are boys, and two-thirds of the girls do not have dark hair. What fraction of Ms. Talbott”s students are girls with dark hair?
![]()
![]()
![]()
![]()
![]()
10. If ![]() , then
, then ![]()

11. If ![]() , and
, and ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
Answer Key 3: Fractions
Concept Review 3
1. 19/35 (Use zip-zap-zup: it”s better than using your calculator!)
2. 20/3 (Change to ![]() .)
.)
3. 8/3 (Divide numerator and denominator by their common factor: 7.)
4. 8/45 (Change to ![]() .)
.)
5. ![]() (Use zip-zap-zup.)
(Use zip-zap-zup.)
6. 4x/3z (Change to ![]() and simplify.)
and simplify.)
7. ![]() (Factor and cancel 4 from the numerator and denominator.)
(Factor and cancel 4 from the numerator and denominator.)
8. –1/(6x) (Change to ![]() and simplify.)
and simplify.)
9. 13/12 (Change to ![]() .)
.)
10. ![]() (Use zip-zap-zup and simplify.)
(Use zip-zap-zup and simplify.)
11. ![]() (As long as
(As long as ![]() .) (Factor as
.) (Factor as 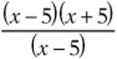 and cancel the common factor. For factoring review, see Chapter 8, Lesson 5.)
and cancel the common factor. For factoring review, see Chapter 8, Lesson 5.)
12. ![]() (Divide numerator and denominator by the common factor: 3. Don”t forget to “distribute” the division in the numerator!)
(Divide numerator and denominator by the common factor: 3. Don”t forget to “distribute” the division in the numerator!)
13. ¼
14. ![]()
15. ![]()
16. ![]() (Knowing how to “convert” numbers back and forth from percents to decimals to fractions can be very helpful in simplifying problems!)
(Knowing how to “convert” numbers back and forth from percents to decimals to fractions can be very helpful in simplifying problems!)
17. Multiply by the reciprocal of the fraction.
18. “Cross-multiply” to get the new numerators, and multiply the denominators to get the new denominator, then just add (or subtract) the numerators.
19. Only common factors. (Factors = terms in products.)
20. Just divide the numbers by hand or on a calculator.
21. 4/9 (Not 4/5! Remember the fraction is a part of the whole, which is 27 students, ![]() .)
.)
22. 27 (If 2/3 are girls, 1/3 are boys: ![]() , so
, so ![]() .)
.)
23. It must have a value between 0 and 1 (“bottom-heavy”).
SAT Practice 3
![]()
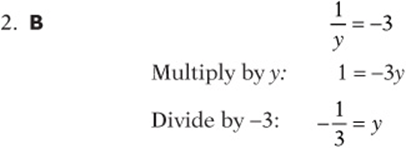
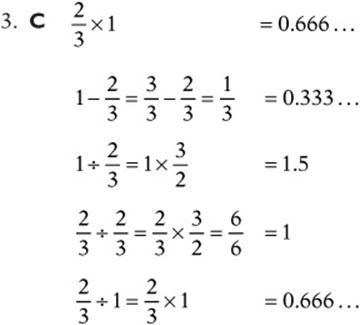
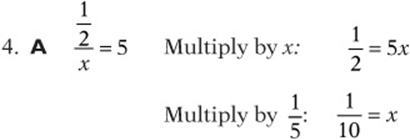

6. A The quotient of opposites is always –1. (Try ![]() and
and ![]() or any other solution.)
or any other solution.)
7. B To turn ![]() into
into ![]() , we only need to multiply by 4!
, we only need to multiply by 4!
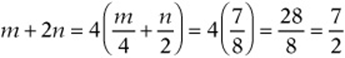
8. E You can solve this by “plugging in” a number for z or by simplifying algebraically. To plug in, pick ![]() and notice that the expression equals
and notice that the expression equals ![]() or 4. Substituting
or 4. Substituting ![]() into the choices shows that only
into the choices shows that only
Alternatively, you can simplify by just multiplying numerator and denominator by z:
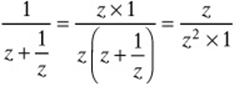
9. C ⅝ are boys, so ⅜ must be girls. Of the girls, ![]() do not have dark hair, so
do not have dark hair, so ![]() do. Therefore,
do. Therefore, ![]() of ⅜ of the class are girls with dark hair.
of ⅜ of the class are girls with dark hair. ![]() .
.
10. 7/6 or 1.16 or 1.17 Begin by subtracting 2/3 from both sides and adding –1/6 to both sides, to simplify. This gives ![]() . Just “reciprocate” both sides or cross-multiply. 6
. Just “reciprocate” both sides or cross-multiply. 6
