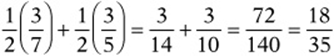SAT Test Prep

CHAPTER 7
ESSENTIAL PRE-ALGEBRA SKILLS

Lesson 4: Ratios and Proportions

Working with Ratios

When you see a ratio—such as 5:6—don”t let it confuse you. If it is not a part-to-part ratio, then just think of it as a fraction. For instance, . If it is a part-to-part ratio, just divide each number by the sum to find the fraction of each part to the whole. For instance, if the ratio of boys to girls in a class is 5:6, then the sum is , so the boys make up 5/11 of the whole class, and the girls make up 6/11 of the whole class. (Notice that these fractions must add up to 1!)

Example:

If a $200 prize is divided up among three people in a 1:4:5 ratio, then how much does each person receive? The total of the parts is . Therefore, the three people receive 1/10, 4/10, and 5/10 of the prize, respectively. So one person gets , another gets, and the other gets .

Working with Proportions

A proportion is just an equation that says that two fractions are equal, as in . Two ways to simplify proportions are with the law of cross-multiplication and with the law of crossswapping. The law of cross-multiplication says that if two fractions are equal, then their “cross-products” also must be equal. The law of cross-swapping says that if two fractions are equal, then “cross-swapping” terms will create another true proportion.

Example:

If we know that , then by the law of cross-multiplication, we know that , and by the law of cross-swapping, that .

In a word problem, the phrase “at this rate” means that you can set up a proportion to solve the problem. A rate is just a ratio of some quantity to time. For instance, your reading rate is in words per minute; that is, it is the ratio of the number of words you read divided by the number of minutes it takes you to read them. (The word per acts like the: in the ratio.) IMPORTANT: When setting up the proportion, check that the units “match up”—that the numerators share the same unit and the denominators share the same unit.

Example:

A bird can fly 420 miles in one day if it flies continuously. At this rate, how many miles can the bird fly in 14 hours?

To solve this, we can set up a proportion that says that the two rates are the same.

Notice that the units “match up”—miles in the numerator and hours in the denominator. Now we can cross-multiply to get and divide by 24 to get miles.

Similarity

Two triangles are similar (have the same shape) if their corresponding angles all have the same measure. If two triangles are similar, then their corresponding sides are proportional.

Example:

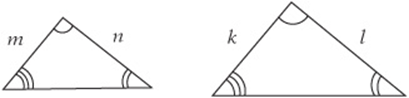
In the figure above,

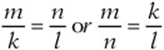
When setting up proportions of sides in similar figures, double-check that the corresponding sides “match up” in the proportion. For instance, notice how the terms “match up” in the proportions above.

Concept Review 4: Ratios and Proportions

1. A speed is a ratio of __________ to __________.

2. An average is a ratio of __________ to __________.

3. Define a proportion:

4. Write the law of cross-multiplication as an “If … then …” statement:

If

then

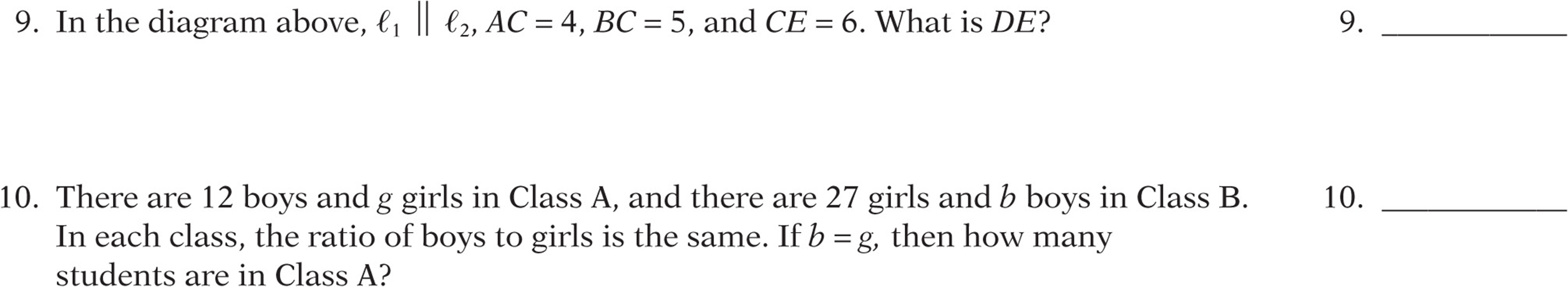
SAT Practice 4: Ratios and Proportions

1. If x is the product of .03 and .2, then x is equivalent to the ratio of 6 to what number?

2. Jar A contains six red marbles and no green marbles. Jar B contains two red marbles and four green marbles. How many green marbles must be moved from Jar B to Jar A so that the ratio of green marbles to red marbles is the same for both jars?

(A) 0

(B) 1

(C) 2

(D) 3

(E) 4

3. 90 students are at a meeting. The ratio of girls to boys at the meeting is 2 to 3. How many girls are at the meeting?

(A) 30

(B) 36

(C) 40

(D) 54

(E) 60

4. If 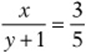, then

5. On a map that is drawn to scale, two towns that are x miles apart are represented as being 4 inches apart. If two other towns are miles apart, how many inches apart would they be on the same map?

(B) 6

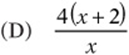
6. If 3,600 baseball caps are distributed to 4 stores in the ratio of 1:2:3:4, what is the maximum number of caps that any one store receives?

(A) 360

(B) 720

(C) 1,080

(D) 1,440

7. David”s motorcycle uses of a gallon of gasoline to travel 8 miles. At this rate, how many miles will it travel on 5 gallons of gasoline?

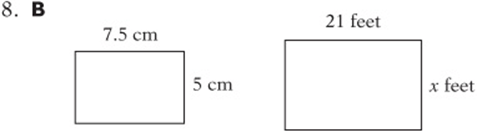
8. On a blueprint that is drawn to scale, the drawing of a rectangular patio has dimensions 5 cm by 7.5 cm. If the longer side of the actual patio measures 21 feet, what is the area, in square feet, of the actual patio?

(A) 157.5

(B) 294.0

(C) 356.5

(D) 441.0

(E) 640.5

9. To make a certain purple dye, red dye and blue dye are mixed in a ratio of 3:4. To make a certain orange dye, red dye and yellow dye are mixed in a ratio of 3:2. If equal amounts of the purple and orange dye are mixed, what fraction of the new mixture is red dye?

Answer Key 4: Ratios and Proportions

Concept Review 4

1. distance to time

2. a sum to the number of terms in the sum

3. A proportion is a statement that two fractions or ratios are equal to each other.

4. If two fractions are equal, then the two “crossproducts” must also be equal.

5. a) 6 = xy

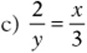
6. $4,800, $7,200, and $12,000. The sum of the parts is , so the parts are 2/10, 3/10, and 5/10 of the whole.

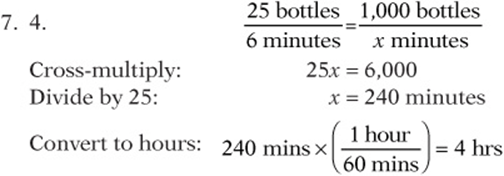
8. m². “At this rate …” implies a proportion:

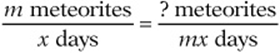
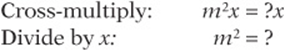
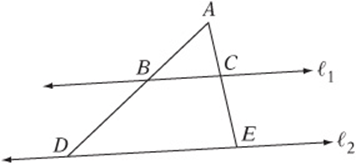
9. 12.5. Because ΔABC is similar to ΔADE. Thus, . Substituting x for DE gives .

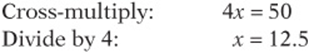
10. 30. Since the ratios are the same, .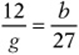

So the number of students in Class .

SAT Practice 4

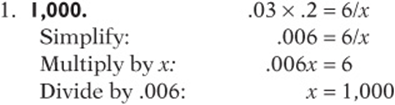
2. D Moving three green marbles from Jar B to Jar A leaves three green marbles and six red marbles in Jar A and one green marble and two red marbles in Jar .

3. B 2:3 is a “part to part” ratio, with a sum of 5. Therefore 2/5 of the students are girls and 3/5 are boys. 2/5 of .

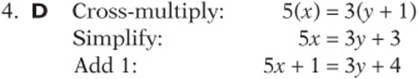
5. D Since the map is “to scale,” the corresponding measures are proportional:

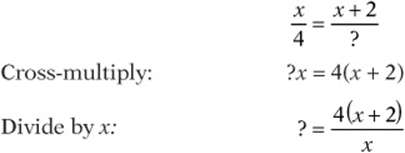
6. D The ratio is a “ratio of parts” with a sum of . The largest part, then, is 4/10 of the whole. 4/10 of .

7. 100. “At this rate” implies a proportion:

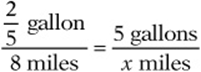
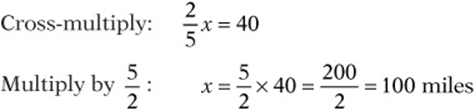
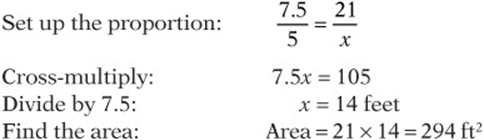
9. C Each ratio is a “ratio of parts.” In the purple dye, the red dye is 3/(3 + 4), or 3/7, of the total, and in the orange dye, the red dye is 3/(3 + 2), or 3/5, of the total. If the mixture is half purple and half orange, the fraction of red is