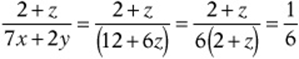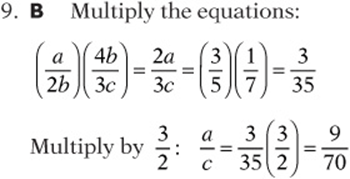SAT Test Prep

CHAPTER 8
ESSENTIAL ALGEBRA I SKILLS

Lesson 2: Systems

Systems

A system is simply a set of equations that are true at the same time, such as these:

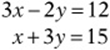
Although many values for x and y “satisfy” the first equation, like (4, 0) and (2, –3) (plug them in and check!), there is only one solution that works in both equations: (6, 3). (Plug this into both equations and check!)

The Law of Substitution

The law of substitution simply says that if two things are equal, you can always substitute one for the other.

Example:

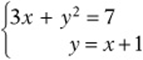
The easiest way to solve this is to substitute the second equation (which is already “solved” for y) into the first, so that you eliminate one of the unknowns. Since , you can replace the y in the first equation with and get

Combining Equations

If the two equations in the system are alike enough, you can sometimes solve them more easily by combining equations. The idea is simple: if you add or subtract the corresponding sides of two true equations together, the result should also be a true equation, because you are adding equal things to both sides. This strategy can be simpler than substitution.

Example:

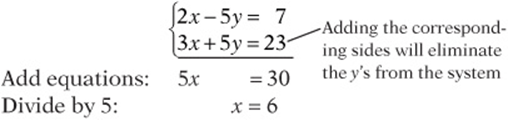
Plug this back in and solve for y:

Special Kinds of “Solving”

Sometimes a question gives you a system, but rather than asking you to solve for each unknown, it simply asks you to evaluate another expression. Look carefully at what the question asks you to evaluate, and see whether there is a simple way of combining the equations (adding, subtracting, multiplying, dividing) to find the expression.

Example:

If and , what is the value of

Don”t solve for x and y! Just notice that equals .

“Letter-Heavy” Systems

An equation with more than one unknown, or a system with more unknowns than equations, is “letter-heavy.” Simple equations and systems usually have just one solution, but these “letter-heavy” equations and systems usually have more than one solution, and you can often easily find solutions simply by “plugging in” values.

Example:

If and , then what is the value of

You can “guess and check” a solution to the equation pretty easily. Notice that , works. If you plug these values into the expression you”re evaluating, you”ll see it simplifies to 2.

Concept Review 2: Systems

1. What is a system?

2. What are two algebraic methods for solving systems?

3. How do you check the solution of a system?

Solve the following systems by substitution, and check your solution.

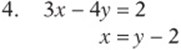
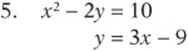
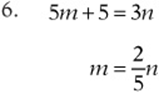
Solve the following systems by combination, and check your solution.

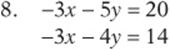
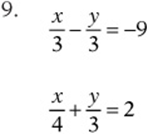
Give three different solutions to each of the following “letter-heavy” systems.

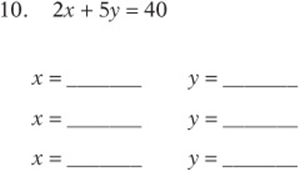
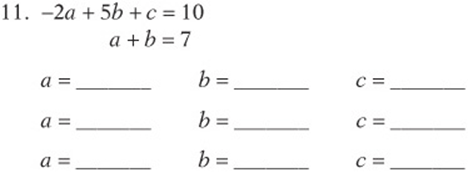
SAT Practice 2: Systems

1. If and , then x =

(A) 6

(B) 7

(C) 8

(D) 9

(E) 10

2. The difference of two numbers is 4 and their sum is –7. What is their product?

(A) –33.0

(B) –28.0

(C) –10.25

(D) 8.25

(E) 10.5

3. If and , what is the value of ?

4. If and , then which of the following expresses p in terms of a?

5. The cost of one hamburger and two large sodas is $5.40. The cost of three hamburgers and one large soda is $8.70. What is the cost of one hamburger?

(A) $1.50

(B) $1.95

(C) $2.40

(D) $2.50

(E) $2.75

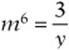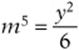6. if and , then which of the following expresses m in terms of y?

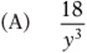
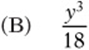
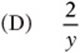
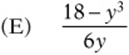
7. The sum of two numbers is 5 and their difference is 2. Which of the following could be the difference of their squares?

(A) –17

(B) –3

(C) 3

(D) 10

(E) 21

8. If , and if x, y, and z are positive, then what is the value of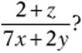

(A) 1/12

(B) 1/6

(C) 1/4

(D) 5/12

(E) 7/12

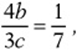9. If and then

Answer Key 2: Systems

Concept Review 2

1. Any set of equations that are true at the same time.

2. Substitution and combination.

3. Plug the solutions back into the equations and check that both equations are true.

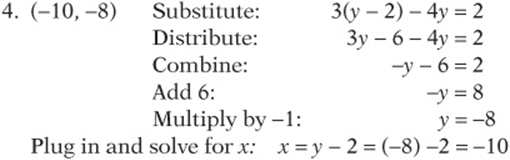
(Look over Lesson 5 if that step was tough!) Zero Product Property: or

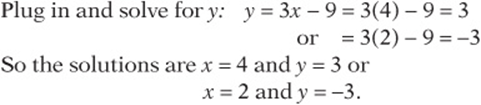
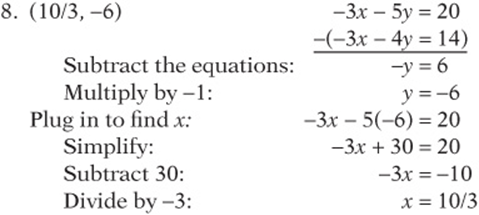
10. There are many solutions. Here are a few:
(0, 8); (20, 0); (10, 4); (5, 6)

11. There are many solutions. Here are a few:
(1, 6, 0); (3, 4, –4); (2, 5, 31); (7, 0, 24)

SAT Practice 2

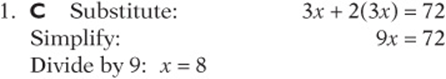
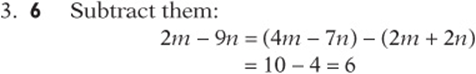
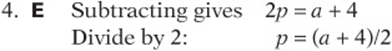
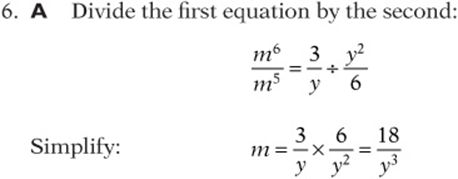
Although you could solve this system by combining, it”s easier to remember the “difference of squares” factoring formula:

8. B This is “letter-heavy,” so you can guess and check a solution, like (2, 11, 4), and evaluate the expression: 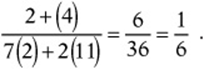Or you can also just add 6z to both sides of the equation to get , then substitute: