SAT Test Prep
CHAPTER 8
ESSENTIAL ALGEBRA I SKILLS
Lesson 3: Working with Exponentials
What Are Exponentials?
An exponential is simply any term with these three parts:
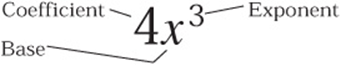
If a term seems not to have a coefficient or exponent, the coefficient or exponent is always assumed to be 1!
Examples:
Expand to Understand
Good students memorize the rules for working with exponentials, but great students understand where the rules come from. They come from simply expanding the exponentials and then collecting or cancelling the factors.
Example:
What is (x5)2 in simplest terms? Do you add exponents to get x7? Multiply to get x10? Power to get x25?
The answer is clear when you expand the exponential. Just remember that raising to the nth power simply means multiplying by itself n times. So 
. Doing this helps you to see and understand the rule of “multiplying the powers.”
Adding and Subtracting Exponentials
When adding or subtracting exponentials, you can combine only like terms, that is, terms with the same base and the same exponent. When adding or subtracting like exponentials, remember to leave the bases and exponents alone.
Example:
Notice that combining like terms always involves the Law of Distribution (Chapter 7, Lesson 2).
Multiplying and Dividing Exponentials
You can simplify a product or quotient of exponentials when the bases are the same or the exponents are the same.
If the bases are the same, add the exponents (when multiplying) or subtract the exponents (when dividing) and leave the bases alone.
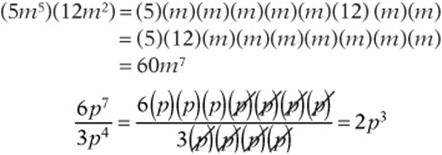
If the exponents are the same, multiply (or divide) the bases and leave the exponents alone.
Example:
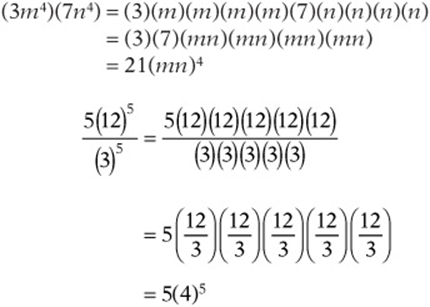
Raising Exponentials to Powers
When raising an exponential to a power, multiply the exponents, but don”t forget to raise the coefficient to the power and leave the base alone.
Example:
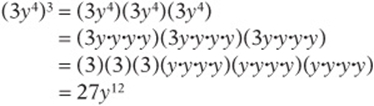
Concept Review 3: Working with Exponentials
1. The three parts of an exponential are the __________, __________, and __________.
2. When multiplying two exponentials with the same base, you should __________ the coefficients, __________ the bases, and __________ the exponents.
3. When dividing two exponentials with the same exponent, you should __________ the coefficients, __________ the bases, and __________ the exponents.
4. When multiplying two exponentials with the same exponent, you should __________ the coefficients, __________ the bases, and __________ the exponents.
5. When dividing two exponentials with the same base, you should __________ the coefficients, __________ the bases, and __________ the exponents.
6. To raise an exponential to a power, you should __________ the coefficient, __________ the base, and __________ the exponents.
Complete the tables:
Simplify, if possible.
SAT Practice 3: Working with Exponentials
1. If 
, then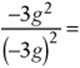 
(A) –1
(E) 1
2. If 
, then m =
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
3. If 
, then 
(A) 1
(B) 3
(C) 6
(D) 9
(E) 12
4. If 
, then 
(A) 20
(B) 40
(C) 80
(D) 100
(E) 200
5. If 
and x is positive, which of the following equals 5y2 in terms of x?
(A) 52x
(C) 252x
(D) 1252x
6. If 
, then 
7. If 
, then what is the effect on the value of p when n is multiplied by 4 and m is doubled?
(A) p is unchanged.
(B) p is halved.
(C) p is doubled.
(D) p is multiplied by 4.
(E) p is multiplied by 8.
8. For all real numbers n,
(A) 2
(B) 2n
(C) 2n1
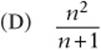
9. If m is a positive integer, then which of the following is equivalent to 
(B) 33m
(D) 9m
(E) 93m
Answer Key 3: Working with Exponentials
Concept Review 3
1. coefficient, base, and exponent
2. multiply the coefficients, keep the bases, and add the exponents.
3. divide the coefficients, divide the bases, and keep the exponents.
4. multiply the coefficients, multiply the bases, and keep the exponents.
5. divide the coefficients, keep the bases, and subtract the exponents.
6. raise the coefficient (to the power), keep the base, and multiply the exponents.
7. –4x coefficient: –1; base: 4; exponent: x
8. (xy)–4 coefficient: –1; base: xy; exponent: –4
9. xy–4 coefficient: x; base: y; exponent: –4
10. (3x)9 coefficient: 1; base: 3x; exponent: 9
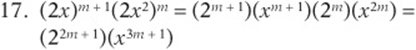
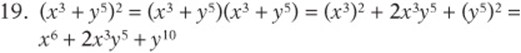
SAT Practice 3
1. B You don”t need to plug in g = –4.1. Just simplify:
If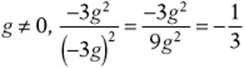 
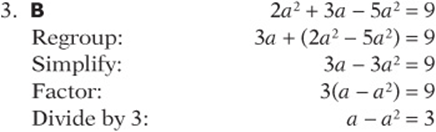
7. B Begin by assuming 
Then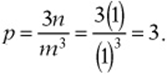 
If n is multiplied by 4 and m is doubled, then 
and 
, so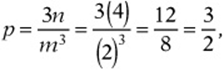 
which is half of the original value.
8. C (Remember that 2n × 2n equals 22n, or 4n, but
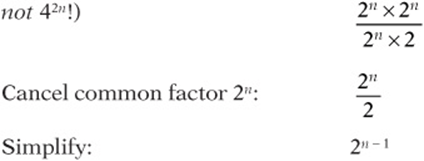
