SAT Test Prep

CHAPTER 9
SPECIAL MATH PROBLEMS

Lesson 5: Counting Problems

The Fundamental Counting Principle

Some SAT questions ask you to count things. Sometimes it”s easy enough to just write out the things in a list and count them by hand. Other times, though, there will be too many, and it will help to use the Fundamental Counting Principle.

To use the Fundamental Counting Principle (FCP), you have to think of the things you”re counting as coming from a sequence of choices. The Fundamental Counting Principle says that the number of ways an event can happen is equal to the product of the choices that must be made to “build” the event.

Example:

How many ways can five people be arranged in a line?

You might consider calling the five people A, B, C, D, and E, and listing the number of arrangements. After a while, though, you”ll see that this is going to take a lot of time, because there are a lot of possibilities. (Not to mention that it”s really easy to miss some of them.) Instead, think of “building” the line with a sequence of choices: first pick the first person, then pick the second person, etc. There are five choices to make, so we”ll have to multiply five numbers. Clearly, there are five people to choose from for the first person in line. Once you do this, though, there are only four people left for the second spot, then three for the third spot, etc. By the Fundamental Counting Principle, then, the number of possible arrangements is .

Example:

How many odd integers greater than 500 and less than 1,000 have an even digit in the tens place?

This seems a lot harder than it is. Again, think of “building” the numbers in question. All integers between 500 and 1,000 have three digits, so building the number involves choosing three digits, so we will multiply three numbers to get our answer. If each number is between 500 and 1,000, then there are only five choices for the first digit: 5, 6, 7, 8, or 9. If the tens digit must be even, we have five choices again: 2, 4, 6, 8, or 0. If the entire number is odd, then we have five choices for the last digit as well: 1, 3, 5, 7, or 9. Therefore, the total number of such integers is .

Using Venn Diagrams to Keep Track of Sets

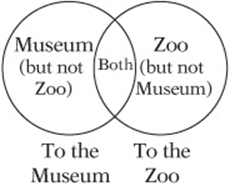
Some counting problems involve “overlapping sets,” that is, sets that contain elements that also belong in other sets. In these situations, Venn diagrams are very helpful for keeping track of things.

Example:

A class of 29 students sponsored two field trips: one to a zoo and one to a museum. Every student attended at least one of the field trips, and 10 students attended both. If twice as many students went to the zoo as went to the museum, how many students went to the zoo?

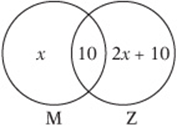
Set up a Venn diagram of the situation. We represent the two sets—those who went to the museum and those who went to the zoo—as two overlapping circles, because some students went to both. Notice that there are three regions to consider. We know that ten students are in the overlapping region, but we don”t know how many are in the other two regions, so let”s use algebra. Let”s say that x students are in the first region, representing those who went to the museum but not to the zoo. This means that students must have gone to the museum altogether. Since twice as many students went to the zoo, the total number in the zoo circle must be . Since 10 of these are already accounted for in the overlapping region, there must be in the third region. So now the diagram should look like this:

The total number of students is 29, so

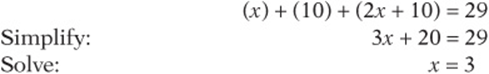
So the number of students who went to the zoo is .

Concept Review 5: Counting Problems

1. What is the fundamental counting principle?

2. How many different four-letter arrangements of the letters LMNO can be made if no letter can be repeated? Answer this first by listing all of the possible arrangements, then by using the Fundamental Counting Principle, and check that the two answers agree.

3. If the first digit of a 3-digit area code cannot be 0 and the second digit is either 0 or 1, then how many different area codes are possible?

4. A baseball team has six players, each of whom can play in any of the three outfield positions: left field, center field, and right field. How many possible different arrangements of these players can the team place in the outfield? (This one is a bit harder to do by listing!)

5. Among a set of 40 sophomores, 20 students take French and 27 students take Spanish. If all of the students take either French or Spanish, how many students take both French and Spanish?

6. A box contains buttons, each of which is either blue or green and has either two or four holes. If there are four times as many blue buttons as green buttons and six times as many four-holed buttons as two-holed buttons, what is the least number of buttons that could be in the box?

SAT Practice 5: Counting Problems

1. A pizzeria offers three different sizes of pizza, two different kinds of crust, and eight different choices for toppings. How many different onetopping pizzas are there to choose from?

(A) 13

(B) 16

(C) 24

(D) 48

(E) 60

0, 2, 4, 6, 8

2. How many different integers between 30 and 70 contain only digits from the list above?

(A) 7

(B) 10

(C) 15

(D) 20

(E) 25

3. In how many ways can you arrange four different paintings in a line on a wall?

(A) 12

(B) 24

(C) 36

(D) 48

(E) 64

4. At Lincoln County High School, 36 students are taking either calculus or physics or both, and 10 students are taking both calculus and physics. If there are 31 students in the calculus class, how many students are there in the physics class?

(A) 5

(B) 8

(C) 11

(D) 15

(E) 21

5. Dave”s stickball team has six players. How many different six-player batting lineups can they make if Dave must bat second and either Zack or Paul must bat first?

(A) 48

(B) 96

(C) 192

(D) 256

(E) 720

6. Maria gave David x cards, gave Tina two more cards than she gave David, and gave Samuel five fewer cards than she gave Tina. In terms of x, how many cards did Maria give Tina, David, and Samuel all together?

7. From a collection of six paintings, four are to be chosen to hang on a wall. How many different arrangements are possible if every painting is different?

(A) 24

(B) 120

(D) 360

(C) 720

(E) 1,296

8. Every marble in a jar has either a dot, a stripe, or both. The ratio of striped marbles to non-striped marbles is 3:1, and the ratio of dotted marbles to nondotted marbles is 2:3. If six marbles have both a dot and a stripe, how many marbles are there all together?

(A) 16

(B) 18

(C) 20

(D) 36

(E) 40

9. An ant must walk from one vertex of a cube to the “opposite” vertex (that is, the vertex that is farthest from the starting vertex) and back again to its starting position. It may only walk along the edges of the cube. For the entire trip, its path must traverse exactly six edges, and it maytravel on the same edge twice. How many different six-edge paths can the ant choose from?

Answer Key 5: Counting Problems

Concept Review 5

1. The number of ways an event can happen is equal to the product of the choices that must be made to “build” the event.

2. Try listing all the “words” that start with L, then all that start with M, and so on:

Whew! 24 in total. Annoying, but not impossible. Using the FCP makes it a lot easier: . That”s it!

3. There are too many possibilities to list, but the FCP makes it easy: We have 9 choices for the first digit, 2 choices for the second digit, and 10 choices for the last digit, and .

4. “Build” the outfield from left to right. You have 6 players to choose from for left field, but then just 5 for center field and 4 for right field. .

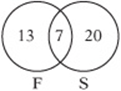
5. Since , there must be 7 students who take both. This Venn diagram shows how it works out:

6. This one”s tough. Say there are g green buttons. If there are four times as many blue buttons as green buttons, then there are 4g blue buttons, so buttons in total. So the total number of buttons must be a multiple of 5. Similarly, if there are n two-holed buttons, there must be 6n four-holed buttons, so the total number of buttons is , so the total number of buttons is also a multiple of 7. The least common multiple of 5 and 7 is 35, so there are 35 buttons: 5 two-holed and 30 four-holed, and 7 green and 28 blue.

SAT Practice 5

1. D Use the .

2. B “Build” the number: If it”s between 30 and 70, it must be a two-digit number that begins with 4 or 6. That”s two choices. The second digit can be anything in the list, so that”s 5 choices.

3. B Since there are four spaces, there are four decisions to make, so four numbers to multiply. You can choose from four paintings for the first spot, then three paintings for the second spot, etc.

4. D If there are 31 students in calculus but 10 of these are also taking physics, then students are taking only calculus. If there are 36 students taking either physics or calculus, but only 31 are taking calculus, then students are taking only physics. Therefore, the Venn diagram should look like this:

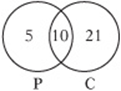
As you can see, students are taking physics.

5. A “Build” the lineup. You have six spots to fill, and thus six decisions to make and six numbers to multiply. You only have two choices for the first spot (Zack or Paul) and one choice for the second spot (Dave), then you have four players left to fill the other slots, so you have four choices for the third spot, then three for the fourth spot, etc.

6. B David gets x cards. Tina gets two more cards than David, which is . Samuel gets five fewer cards than Tina, which is . So all together, .

7. C You have six choices for the first spot, then five for the second, then four for the third and three for the fourth.

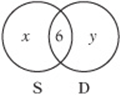
8. E Set up the Venn diagram: Since the ratio of striped marbles to nonstriped marbles is 3:1, , and since the ratio of dotted marbles to nondotted marbles is 2:3, and therefore . Substituting, we get or , so . Plug this back in to get

9. 36 Draw the cube. To get from any vertex to its opposite vertex, the ant has possible paths. To see why, trace a path and notice it has three choices for the first edge, then two for the second, then only one option for the third. Since it must return to the opposite vertex, it has different paths it can take back.