SAT Test Prep
CHAPTER 9
SPECIAL MATH PROBLEMS
Lesson 6: Probability Problems
Probability
A probability is a number between 0 and 1 that represents the likelihood of an event. An event with a probability of 0 is impossible, and an event with a probability of 1 is certain. Most probabilities, of course, are somewhere in between 0 and 1. For instance, the probability of rolling a 5 on a fair die is ![]() . It”s best to think of a probability as a part-to-whole ratio. There are six possible outcomes when you roll a die (the whole), but only one of them is 5 (the part). Thus, the probability of rolling a 5 is
. It”s best to think of a probability as a part-to-whole ratio. There are six possible outcomes when you roll a die (the whole), but only one of them is 5 (the part). Thus, the probability of rolling a 5 is ![]() .
.
Example:
What is the probability of rolling a sum of 5 on two dice?
Here is a table showing all the possible sums on a roll of two dice:
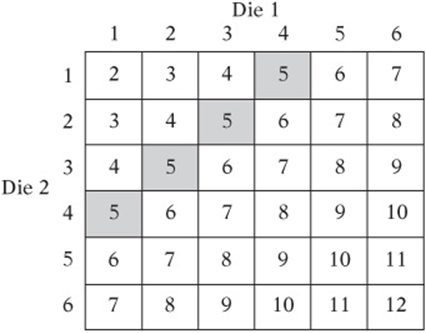
Clearly, there are four ways of getting a sum of 5 out of a possible 36, so the probability is ![]() .
.
Geometrical Probability
An SAT question may ask you to find the probability that something hits a certain region, like a dart hitting a dartboard. In these situations, the probability is just the ratio of the particular area to the entire area.
Example:
A landing target for skydivers consists of two concentric circles. The smaller circle has a radius of 3 meters, and the larger one has a radius of 6 meters. If a skydiver hits the target, what is the probability that she hits the smaller circle?
It might help to sketch the target:
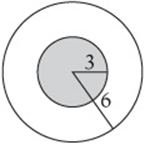
If she hits the target, then she hits an area that is ![]() square meters in area. The smaller circle, though, is only
square meters in area. The smaller circle, though, is only ![]() square meters in area, so the probability that she lands within the smaller region should be just
square meters in area, so the probability that she lands within the smaller region should be just ![]() .
.
Concept Review 6: Probability Problems
1. The probability of an impossible event is __________.
2. The probability of an event that is certain is __________.
3. If a jar contains 3 red marbles, 4 white marbles, and 5 blue marbles, then what is the probability of randomly choosing
a red marble? __________
a white marble? __________
a blue marble? __________
4. A jar contains 5 red marbles and 10 white marbles.
What is the probability of drawing a red marble? __________
If 3 more red marbles are added, then what is the probability of drawing a red marble? __________
5. A jar contains 24 red and blue marbles. If the probability of selecting a red marble at random is ⅜, then how many red marbles must be added so that the probability of randomly selecting a red marble becomes ½?
6. A jar contains only black, white, and red marbles. The probability of choosing a white marble is ![]() . If there are 4 times as many red marbles as black marbles, what is the least possible number of marbles in the jar?
. If there are 4 times as many red marbles as black marbles, what is the least possible number of marbles in the jar?
SAT Practice 6: Probability Problems
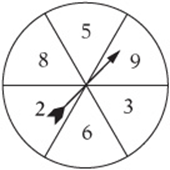
1. The figure above shows a spinner in the middle of a disc divided into six equal parts, each labeled with a number. What is the probability that the spinner will land on a number that is either even or greater than 5?
![]()
![]()
![]()
![]()
![]()
2. A jar contains 10 blue marbles, 8 green marbles, and 14 red marbles. How many green marbles must be added so that the probability of choosing a green marble at random is ![]() ?
?
(A) 16
(B) 42
(C) 40
(D) 64
(E) 72
3. A fair six-sided die has faces bearing the numbers 1, 2, 3, 4, 5, and 6. When the die is thrown, the numbers on the five visible faces are added. What is the probability that this sum is greater than 18?
![]()
![]()
![]()
![]()
![]()
4. A target consists of three concentric circles, with radii of 1 meter, 2 meters, and 3 meters. If an arrow that hits the target hits any point on the target with equal probability, what is the probability that an arrow that hits the target falls in the outermost region (between the second and third circles)?
![]()
![]()
![]()
![]()
![]()
5. The probability of a meteor shower occurring in the skies above a particular island on any given night is ![]() Independently, the probability that any given night will be cloudless is
Independently, the probability that any given night will be cloudless is ![]() What is the probability that, on any given night, there will be a meteor shower and it will be cloudless?
What is the probability that, on any given night, there will be a meteor shower and it will be cloudless?
![]()
![]()
![]()
![]()
![]()
6. A basket contains red, green, and yellow balls, all of equal size. The probability of choosing a green ball at random is ![]() If there are 3 times as many red balls as yellow balls, what is the probability of choosing a yellow ball at random?
If there are 3 times as many red balls as yellow balls, what is the probability of choosing a yellow ball at random?

7. A certain disease occurs in 1 person out of every 101 people. A test for the disease is 100% accurate for patients with the disease and 99% accurate for patients without it. That is, it gives a “false positive” 1% of the time even if the person tested doesn”t have the disease. If you take this test and it returns a positive result, what is the probability that you have the disease?
(A) 1
(B) .99
(C) .95
(D) .50
(C) .01
Answer Key 6: Probability Problems
Concept Review 6
1. 0
2. 1
3. 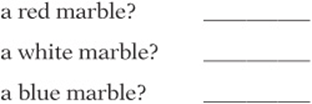
4. What is the probability of drawing a red marble? ![]()
If 3 more red marbles are added, what is the probability of drawing a red marble? ![]()
5. If the jar contains 24 red and blue marbles and the probability of selecting a red marble at random is ![]() there must be
there must be ![]() red marbles, and
red marbles, and ![]() blue marbles. If the probability of drawing a red marble is to be ½, there must be as many red as blue marbles, so you must add
blue marbles. If the probability of drawing a red marble is to be ½, there must be as many red as blue marbles, so you must add ![]() marbles.
marbles.
6. Let”s say that the probability of drawing a black marble is x. Since there are 4 times as many red marbles as black marbles, the probability of drawing a red marble must be 4x. The probability of choosing a white marble is ![]() Since we are certain to pick one of these colors, the sum of all of these probabilities must be 1:
Since we are certain to pick one of these colors, the sum of all of these probabilities must be 1: ![]()

Therefore, ![]() of the marbles are black,
of the marbles are black, ![]() of the marbles are red, and
of the marbles are red, and ![]() of the marbles are white. The least common denominator of these fractions is 15, which means that 15 is the least possible number of marbles. In that case, there are 1 black marble, 4 red marbles, and 10 white marbles.
of the marbles are white. The least common denominator of these fractions is 15, which means that 15 is the least possible number of marbles. In that case, there are 1 black marble, 4 red marbles, and 10 white marbles.
SAT Practice 6
1. D Put an “x” through any number that is either even or greater than 5, or both. This gives us 8, 9, 2, and 6, which is 4 out of the 6 spaces, giving a probability of ![]() or
or ![]() .
.
2. D If the probability of choosing a green marble is to be ![]() , then
, then ![]() of the marbles should be green and ¼ not green. There are 10 blue and 14 red, for a total of 24 “not green” marbles, and this will not change, since you are adding only green marbles. If this is ¼ of the total, then there must be
of the marbles should be green and ¼ not green. There are 10 blue and 14 red, for a total of 24 “not green” marbles, and this will not change, since you are adding only green marbles. If this is ¼ of the total, then there must be ![]() marbles total after you add the extra green marbles. The jar now contains
marbles total after you add the extra green marbles. The jar now contains ![]() marbles, so you must add
marbles, so you must add ![]() green marbles.
green marbles.
3. B The six sides of a die add up to ![]() . The sum of any five faces can be greater than 18 only if the “down” face is 1 or 2 (so that the sum of the other faces is either
. The sum of any five faces can be greater than 18 only if the “down” face is 1 or 2 (so that the sum of the other faces is either ![]() or
or ![]() This is 2 possibilities out of 6 for a probability of
This is 2 possibilities out of 6 for a probability of ![]() .
.
4. E Sketch the target:
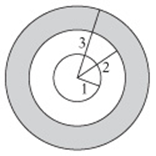
You want to know the probability of the arrow hitting the outermost ring, which is the ratio of the area of the ring to the entire area of the target.
The area of the whole target is ![]() . The area of the outermost ring is
. The area of the outermost ring is ![]() (subtract the area of the middle circle from the area of the big circle)
(subtract the area of the middle circle from the area of the big circle) ![]() . So the probability is
. So the probability is ![]() .
.
5. A Consider a stretch of 100 consecutive nights. If the probability of a meteor shower is ![]() , then we should expect a meteor shower on
, then we should expect a meteor shower on ![]() of those nights. If only
of those nights. If only ![]() of the nights are cloudless, though, then
of the nights are cloudless, though, then ![]() of the nights with a meteor shower, on average, should be cloudless. This gives a probability of
of the nights with a meteor shower, on average, should be cloudless. This gives a probability of ![]() Mathematically, we can just multiply the two probabilities (as long as they are independent) to get the joint probability:
Mathematically, we can just multiply the two probabilities (as long as they are independent) to get the joint probability: ![]() .
.
6. ![]() Call the probability of choosing a yellow ball x. If there are three times as many red balls as yellow balls, the probability of choosing a red ball must be 3x. The probability of choosing a green ball is
Call the probability of choosing a yellow ball x. If there are three times as many red balls as yellow balls, the probability of choosing a red ball must be 3x. The probability of choosing a green ball is ![]() These probabilities must have a sum of 1:
These probabilities must have a sum of 1:

7. D Most people would say that this probability is quite high, because the test is so reliable. But intuition is often wrong. Imagine that you test 101 people. Of these, on average, one will have the disease, and 100 will not. Since the test is 100% accurate for those who have the disease, that person will test positive. Of the 100 who do not have the disease, 99 will test negative, but one will test positive, because of the 1% “false positive” rate. So of those two who test positive, only one will have the disease; thus, the probability is ½.