SAT Test Prep

CHAPTER 10
ESSENTIAL GEOMETRY SKILLS

Lesson 4: Coordinate Geometry

Plotting Points

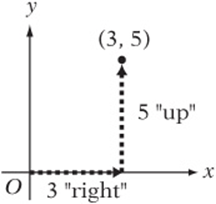
Some SAT questions may ask you to work with points on the x-y plane (also known as the coordinate plane or the Cartesian plane, after the mathematician and philosopher René Descartes). When plotting points, remember these four basic facts to avoid the common mistakes:

• The coordinates of a point are always given alphabetically: the x-coordinate first, then the y-coordinate.

• The x-axis is always horizontal and the y-axis is always vertical.

• On the x-axis, the positive direction is to the right of the origin (where the x and y axes meet, point (0,0)).

• On the y-axis, the positive direction is up from the origin (where the x and y axes meet, point (0,0)).

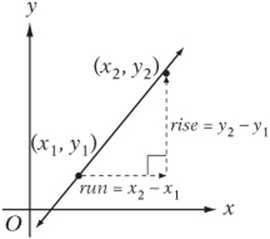
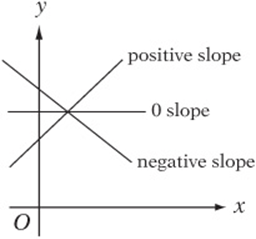
Working with Slopes

Every line has a slope, which is the distance you move up or down as you move one unit to the right along the line. Imagine walking between any two points on the line. As you move, you go a certain distance “up or down.” This distance is called the rise. You also go a certain distance “left or right.” This distance is called the run.

The slope is simply the rise divided by the run.

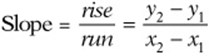
You should be able to tell at a glance whether a slope has a positive, negative, or zero slope. If the line goes up as it goes to the right, it has a positive slope. If it goes down as it goes to the right, it has a negative slope. If it”s horizontal, it has a zero slope.

If two lines are parallel, they must have the same slope.

Finding Midpoints

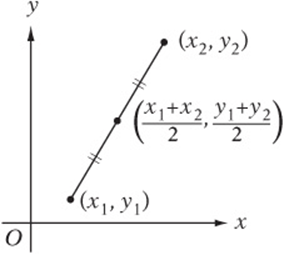
The midpoint of a line segment is the point that divides the segment into two equal parts.

Think of the midpoint as the average of the two endpoints.

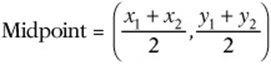
Concept Review 4: Coordinate Geometry

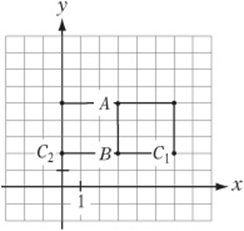
Questions 1–10 refer to the figure below. Horizontal and vertical lines are spaced 1 unit apart.

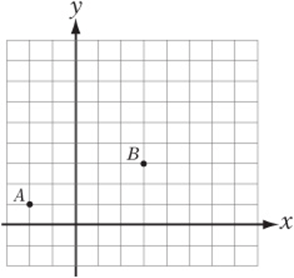
6. Draw a line through B that is parallel to the x-axis and label it ℓ₂.

7. Draw the line and label it ℓ₃.

8. If point A is reflected over ℓ₂, what are the coordinates of its image? __________

9. If line segment is rotated 90 clockwise about point B, what are the coordinates of the image of point A? __________

10. If point B is the midpoint of line segment , what are the coordinates of point C? __________

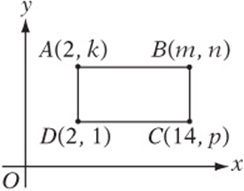
Rectangle ABCD has an area of 108.

Note: Figure not drawn to scale.

Questions 11–15 pertain to the figure above.

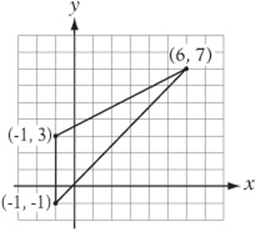
Questions 16–18 pertain to the figure above.

16. What is the area of the triangle above? __________

17. If the triangle above were reflected over the line x = 3, what would be the least x-coordinate of any point on the triangle? __________

18. If the triangle above were reflected over the line , what would the area of the new triangle be? __________

SAT Practice 4: Coordinate Geometry

1. If point A has coordinates (3, 5), point B has coordinates (3, 2), and ABCD is a square, which of the following could be the coordinates of point C?

(A) (4, 2)

(B) (6, 2)

(C) (6, 6)

(D) (4, 6)

(E) (8, 2)

2. If ℓ₁ is a horizontal line passing through (1, 8) and ℓ₂ is a vertical line passing through (–3, 4), then at what point do ℓ₁ and ℓ₂ intersect?

(A) (–3, 8)

(B) (1, 4)

(C) (–1, 6)

(D) (–2, 12)

(E) (0,0)

3. The point (–3, 4) is on a circle with its center at the origin. Which of the following points must also be on the circle?

I. (0, –5)

II. (–4, –3)

III. (3, 4)

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III

4. If the point (3, –7) is the center of a circle and the point (8, 5) is on the circle, what is the circumference of the circle?

(A) 13π

(B) 15π

(C) 18π

(D) 25π

(E) 26π

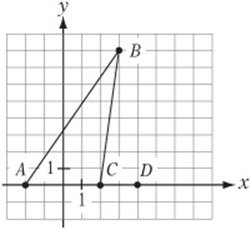
5. In the figure above, point E is to be drawn so that ΔCDE has the same area as ΔABC. Which of the following could be the coordinates of E?

(A) (16, 5)

(B) (3, 8)

(C) (5, 12)

(D) (2, 16)

(E) (4, 24)

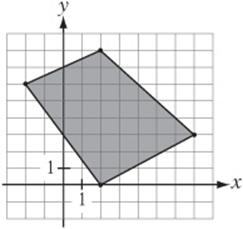
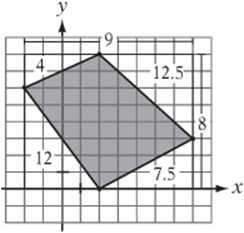
6. What is the area, in square units, of the shaded region in the figure above?

(A) 32

(B) 33

(C) 34

(D) 35

(E) 36

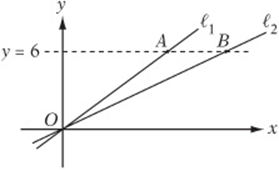
Note: Figure not drawn to scale.

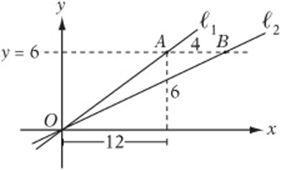
7. Points A and B lie on the line , as shown above. Lines ℓ₁ and ℓ₂ pass through the origin, and ℓ₁ has a slope of ½. If the distance from A to B is 4, what is the slope of line ℓ₂?

Answer Key 4: Coordinate Geometry

Concept Review 4

1. (–2, 1)

2. (0.5, 2)

3. 2/5

4. Your line should be vertical (straight up and down) and pass through B.

5. The x-coordinate of all the points is 3, so ℓ₁ can be described by the equation .

6. ℓ₂ should be horizontal (straight across) and pass through B.

7. ℓ₃ should be a horizontal (straight across) line one unit below the x-axis.

8. (–2, 5)

9. (1, 8) (Notice that the new segment must be the same length as AB, but its slope is the negative reciprocal of AB”s slope, that is, –5/2.)

10. (8, 5)

11. The area of the rectangle is 108, and its length DC is . So its height is . Therefore, , and .

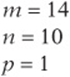
12. AC is the hypotenuse of a right triangle with legs of 9 and 12. This is a 3-4-5 triangle times 3—a 9-12-15 triangle—so AC is 15. The perimeter of the rectangle is . So the ratio of the diagonal to the perimeter is .

13. The slope of DB is 3/4, or .75.

14. AC and DB intersect at the midpoint of each segment. The midpoint of AC is .

15. (26, 19)

16. Use the left side of the triangle as the base. This way, the base is vertical and the height is horizontal, so the lengths are easier to find. The base is 4 units and the height is 7 units, so the area is .

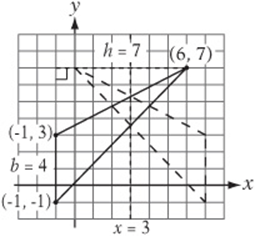
17. The reflection of the triangle over the line is shown above. The “leftmost” point has an x-coordinate of 0.

18. No matter how the triangle is reflected, the area remains the same. The area is still 14.

SAT Practice 4

1. B The vertices of a square must always be listed in consecutive order, so point C must follow consecutively after B and can be in either position shown in the figure at right. Therefore, C can be at (0, 2) or (6, 2).

2. A The horizontal line passing through (1, 8) is the line , and the vertical line passing through (–3, 4) is the line . So they intersect at (–3, 8).

3. E The distance from (0, 0) to (–3, 4) is 5, which is the radius of the circle. Therefore, any point that is 5 units from the origin is also on the circle. Each of the given points is also 5 units from the origin.

4. E The distance from (3, –7) to (8, 5) is 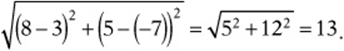The circumference is .

5. D ΔABC has a base of 4 and height of 8, so its area is . Since the base of ΔCDE is 2, its height must be 16 if it is to have the same area as ΔABC. The y-coordinate of E, then, must be 16 or –16.

6. E Draw a rectangle around the quadrilateral as in the figure at right. The rectangle has an area of . If we “remove” the areas of the four right triangles from the corners, the area of the shaded region will remain.

7. 3/8 The y-coordinate of point A is 6, which means the “rise” from O to A is 6. Since the slope of ℓ₁ is ½, the “run” must be 12. The “run” from O to B is , and the “rise” is 6, so the slope of ℓ² is .