SAT Test Prep
CHAPTER 11
ESSENTIAL ALGEBRA 2 SKILLS
Lesson 6: Negative and Fractional Exponents
Exponents Review
In Chapter 8, Lesson 3, we discussed the practical definition of exponentials:
The expression xn means x multiplied by itself n times.
This is a useful definition when you need to evaluate something like 43: you simply multiply 
and get 64. But what about expressions like 40 or 4–3 or 41/2? How do you multiply 4 by itself 0 times, or –3 times, or half of a time? It doesn”t make much sense to think of it that way. So to understand such expressions, you must expand your understanding of exponents.
Zero and Negative Exponents
Using what you have learned in Lesson 1 of this chapter, what are the next three terms of this sequence?
The rule seems to be “divide by 3,” so the next three terms are 1, 
, and 
.
Now, what are the next three terms of this sequence?
Here, the rule seems to be “reduce the power by 1,” so that the next three terms are 30, 3–1, and 3–2.
Notice that the two sequences are exactly the same, that is, 
, 
, 
, and 
. This means that the pattern can help us to understand zero and negative exponents: 
, 
, and 
. Now, here”s the million-dollar question:
Without a calculator, how do you write 3–7 without a negative exponent?
If you follow the pattern you should see that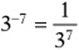 
and, in general:
Notice that raising a positive number to a negative power does not produce a negative result. For instance 3–2 does not equal –9; it equals .
Fractional Exponents
What if a number is raised to a fractional exponent? For instance, what does 81/3 mean? To understand expressions like this, you have to use the basic rules of exponents from Chapter 8, Lesson 3. Specifically, you need to remember that 
.
Using the rule above, 
. In other words, when you raise 81/3 to the 3rd power, the result is 8. This means that 81/3 is the same as the cube root of 8, and, in general:
The expression x1/n means 
, or the nth root of x. For example,
can be written as a1/2.
Example:
What is the value of 163/4?
The first step is to see that 163/4 is the same as (161/4)3(because 
. Using the definition above, 161/4 is the 4th root of 16, which is 2 (because 
). So 
.
The expression xm/n means the nth root of x raised to the mth power. For instance, 43/2 means the square root of 4 raised to the third power, or 
.
Concept Review 6: Negative and Fractional Exponents
Evaluate the following expressions without a calculator.
1. 5–2
2. 91/2
3. 2–5
4. 25–1/2
5. 43/2
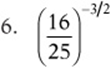
Simplify the following expressions, eliminating any negative or fractional exponents.
7. x1/3
8. (4g)1/2
9. 4x–2
10. (4y)–2
11. (9m)3/2
12. (27b)1/3/(9b)–1/2
13. If 
, what is the value of x?
14. If 
, what is the value of b?
15. If 
, what is the value of 23m?
SAT Practice 6: Negative and Fractional Exponents
1. If 
, then what is the value of 4–n?
2. If 
, then 
(A) –52
(B) 5–2
(D) 51/2
3. If 
, then m =
4. For all values of n,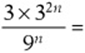 
(A) 3
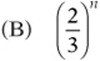
(C) 3n
(D) 92
(E) 9n
5. If x is a positive number, then 
(A) x3/4
(B) x–(1/4)
(C) x3/4
6. If 
and x is positive, then 
(A) x1/5
(B) x1/8
(C) x8/15
(D) x8
(E) x15
Answer Key 6: Negative and Fractional Exponents
Concept Review 6
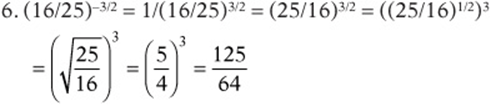
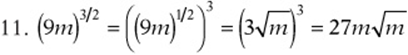
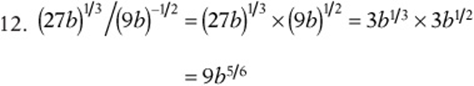
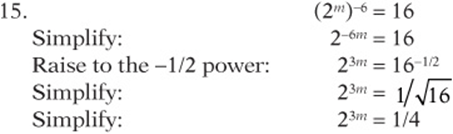
SAT Practice 6
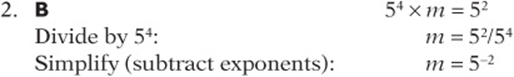
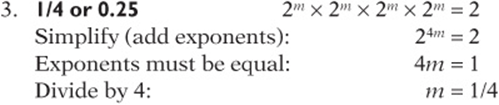
Perhaps a simpler method is to simply pick n to be 0 (because n can be any number). This gives 
. The only choice that equals 3 when 
is (A).
(Remember the quick way to add fractions: “zip-zap-zup” from Chapter 7, Lesson 3.)