Cracking the New SAT with 4 Practice Tests, 2016 Edition (2015)
Part IV. How to Crack the Math Test
Chapter 16. Geometry
Now that you’ve had some review and practice in coordinate geometry, it’s time to learn a few more geometry rules. The SAT Math Test contains five or six questions that test your basic geometry knowledge on topics like lines and angles, triangles, and circles. This chapter covers each of these topics and more and provides a step-by-step walk-through for each type of problem.
GEOMETRY ON THE SAT
We covered coordinate geometry in Chapter 15. But in addition to coordinate geometry questions, there will be five or six questions on the SAT that test your knowledge of basic geometry rules. Well, kinda. At the beginning of each Math section, you are provided with the following:
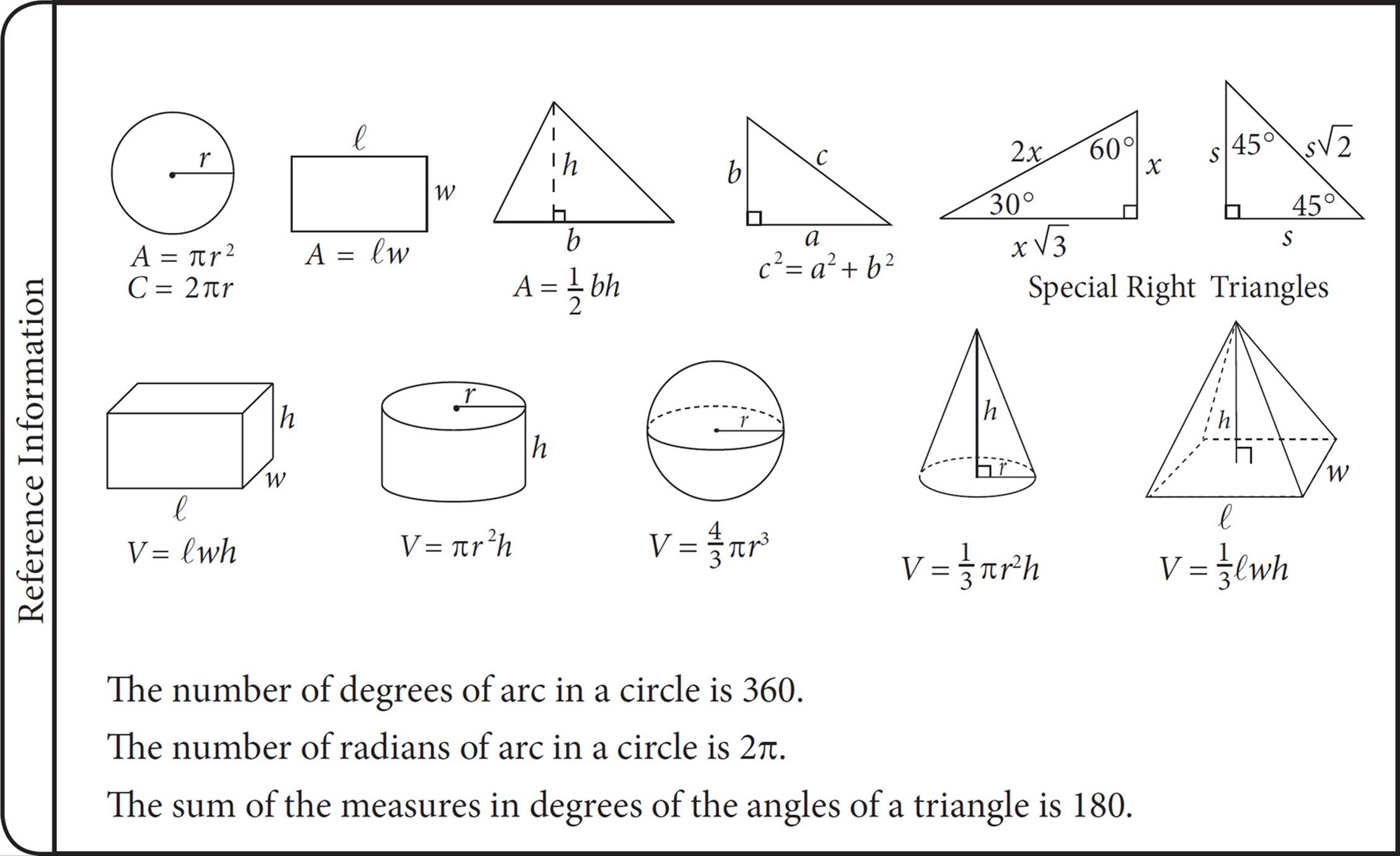
This box of information contains some of what you’ll need to tackle geometry on the SAT. In this chapter, we’ll cover how to approach geometry questions and what else you will need to know to handle geometry questions on the SAT.
Geometry: Basic Approach
For the handful of non-coordinate geometry questions that appear on the SAT, The Princeton Review recommends this step-by-step approach:
1.Draw a figure if a figure is not provided. Also, if there is a figure provided, but the question has a “Note: figure not drawn to scale” by the figure, you might also want to redraw the figure using the information in the question.
2.Label the figure with any information given in the text of the question. Sometimes, you can plug in for parts of the figure as well.
3.Write down formulas that you might need for the question.
4.Ballpark if you’re stuck or running short on time.
These four steps, combined with the techniques you’ve learned in the rest of this book and the geometry concepts this chapter will cover, will enable you to tackle any geometry question you might run across on the SAT.
Before we dive in to the nitty-gritty, let’s try a problem using the approach.
![]()

25.In ΔABC (not shown), ∠ABC = 60° and AC ⊥ BC. If AB = x, then what is the area of ΔABC, in terms of x ?
A)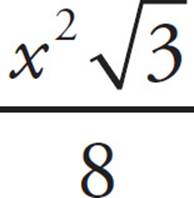
B)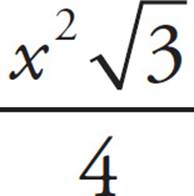
C)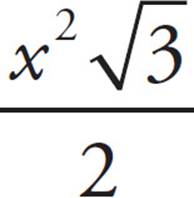
D)x2 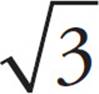
Here’s How to Crack It
Follow the geometry approach steps. Start by drawing the figure. If AC ⊥ BC, then ΔABC is a right triangle with the right angle at point C:
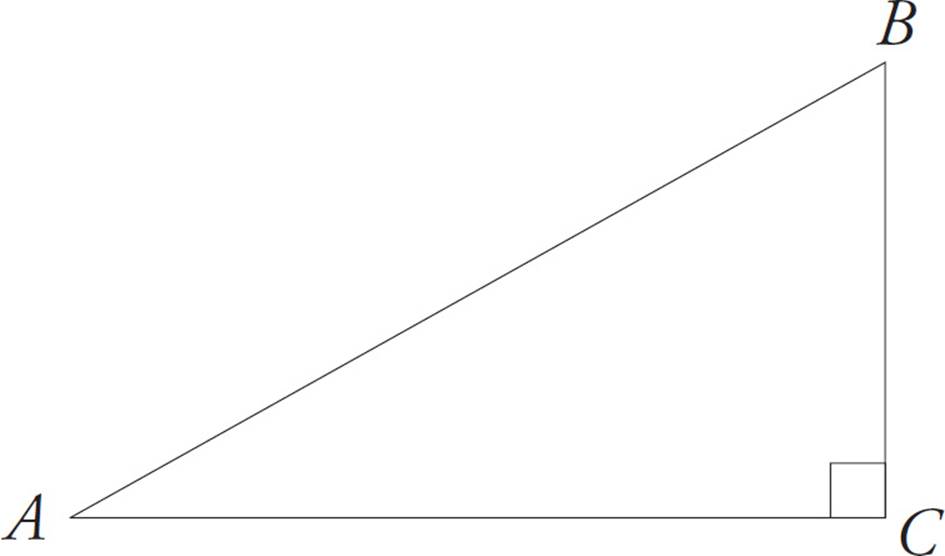
The next step is to label what you know. ∠ABC = 60° can go right into the diagram. Because AB = x, you can plug in for x; make x = 4. Label this information into the diagram:
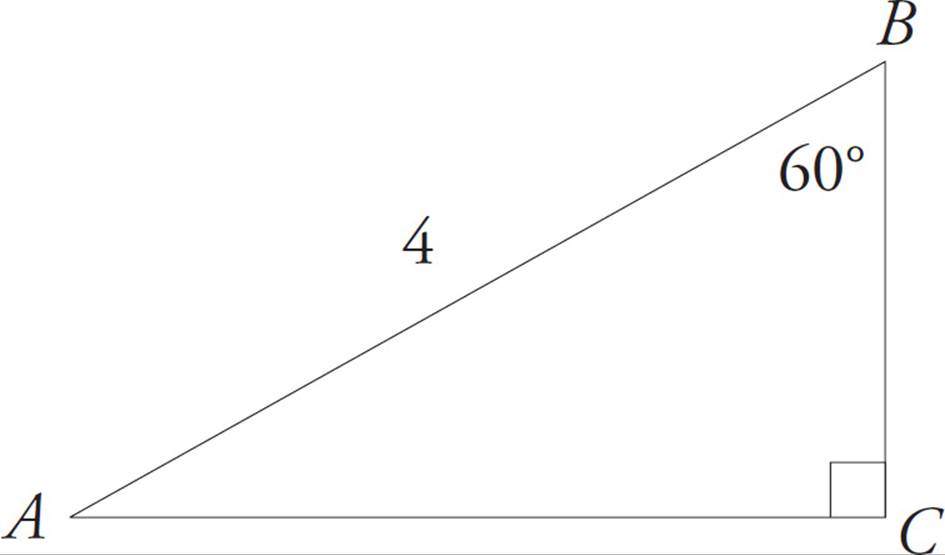
Next, figure out what else you know. Because there are 180° in a triangle, ∠BAC = 180 − 90 − 60 = 30°. This is a 30°-60°-90° special right triangle, information about which is given in the box of information at the start of the section. Based on the figure given in the box, the hypotenuse is equal to 2x. (Note that this is a DIFFERENT x than what you plugged in for, because the SAT wants to confuse you on purpose.) So, if the hypotenuse is 4, then x = ![]() = 2; this is the side opposite the 30° angle, BC. The remaining side, AC, is x
= 2; this is the side opposite the 30° angle, BC. The remaining side, AC, is x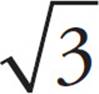 , which is 2
, which is 2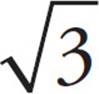 . Label all this information into your diagram:
. Label all this information into your diagram:
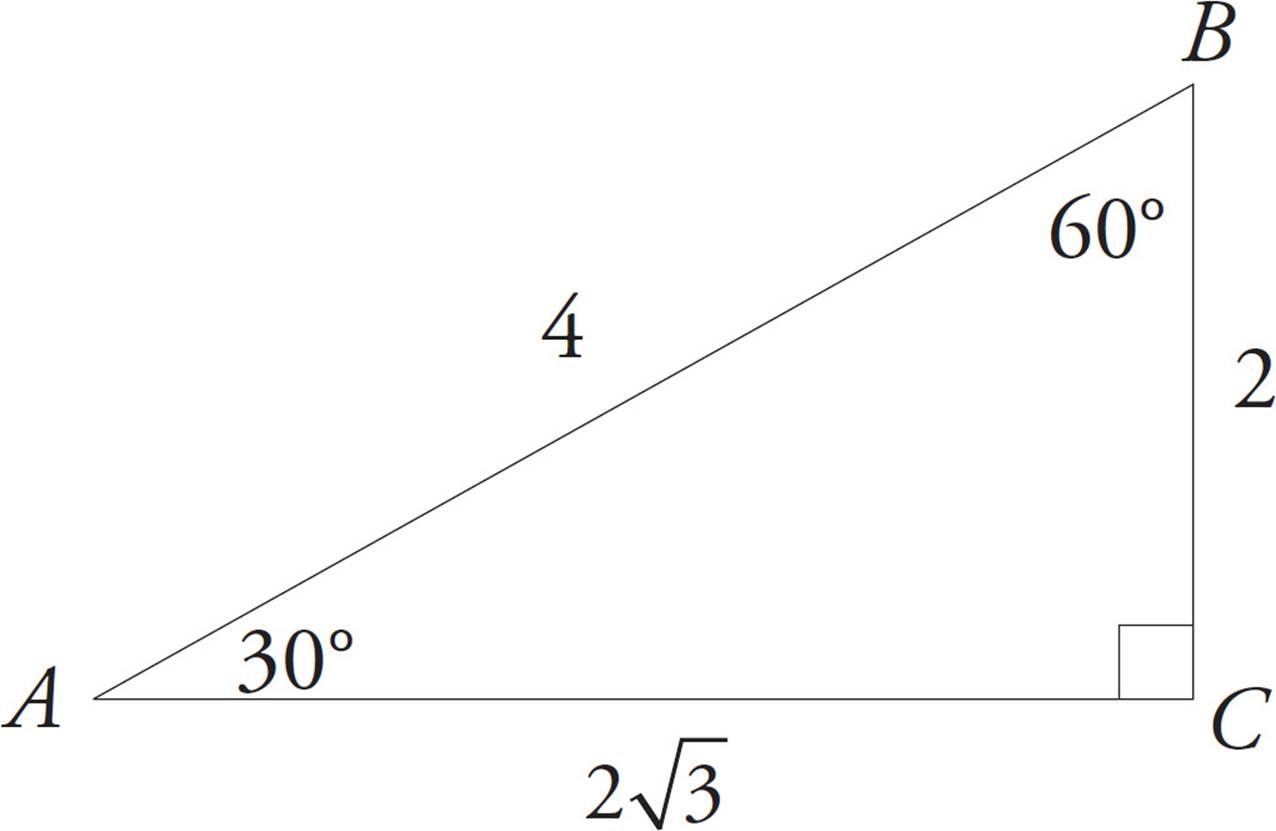
Now write down the formula you need. The question is asking for the area, so use the area of a triangle formula from the box: A = ![]() bh. Fill in what you know; because this is a right triangle, you can use the two legs of the triangle as the base and the height. Make b = 2
bh. Fill in what you know; because this is a right triangle, you can use the two legs of the triangle as the base and the height. Make b = 2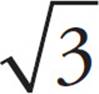 and h = 2 in the equation and solve: A =
and h = 2 in the equation and solve: A = ![]() (2
(2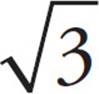 )(2) = 2
)(2) = 2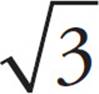 . This is your target; circle it. Now, plug in x = 4 (that’s the x from the problem, NOT the xfrom the information in the box!) into each answer choice and eliminate what doesn’t equal 2
. This is your target; circle it. Now, plug in x = 4 (that’s the x from the problem, NOT the xfrom the information in the box!) into each answer choice and eliminate what doesn’t equal 2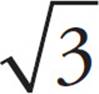 . The only choice that works is (A).
. The only choice that works is (A).
![]()
Now that we’ve covered the approach to geometry questions, let’s look more closely at some of the geometry concepts you’ll need for these problems.
Lines and Angles
Here are the basic rules you need to know for questions about lines and angles on the SAT.
1.A circle contains 360 degrees.
Every circle contains 360 degrees. Each degree is 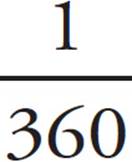 of the total distance around the outside of the circle. It doesn’t matter whether the circle is large or small; it still has exactly 360 degrees.
of the total distance around the outside of the circle. It doesn’t matter whether the circle is large or small; it still has exactly 360 degrees.
2.When you think about angles, remember circles.
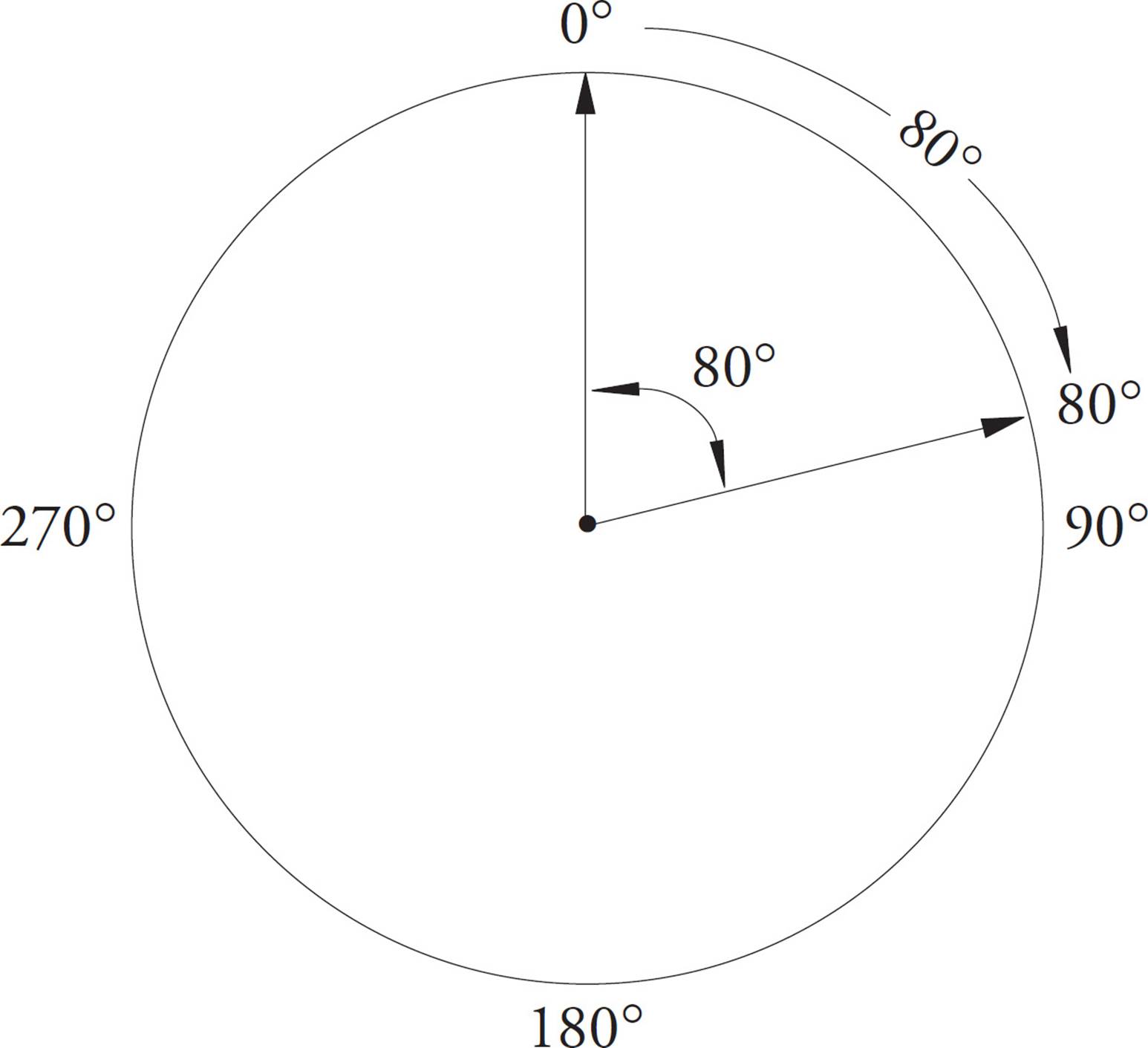
An angle is formed when two line segments extend from a common point. If you think of the point as the center of a circle, the measure of the angle is the number of degrees enclosed by the lines when they pass through the edge of the circle. Once again, the size of the circle doesn’t matter; neither does the length of the lines.
Please refer to the figure below for clarification.
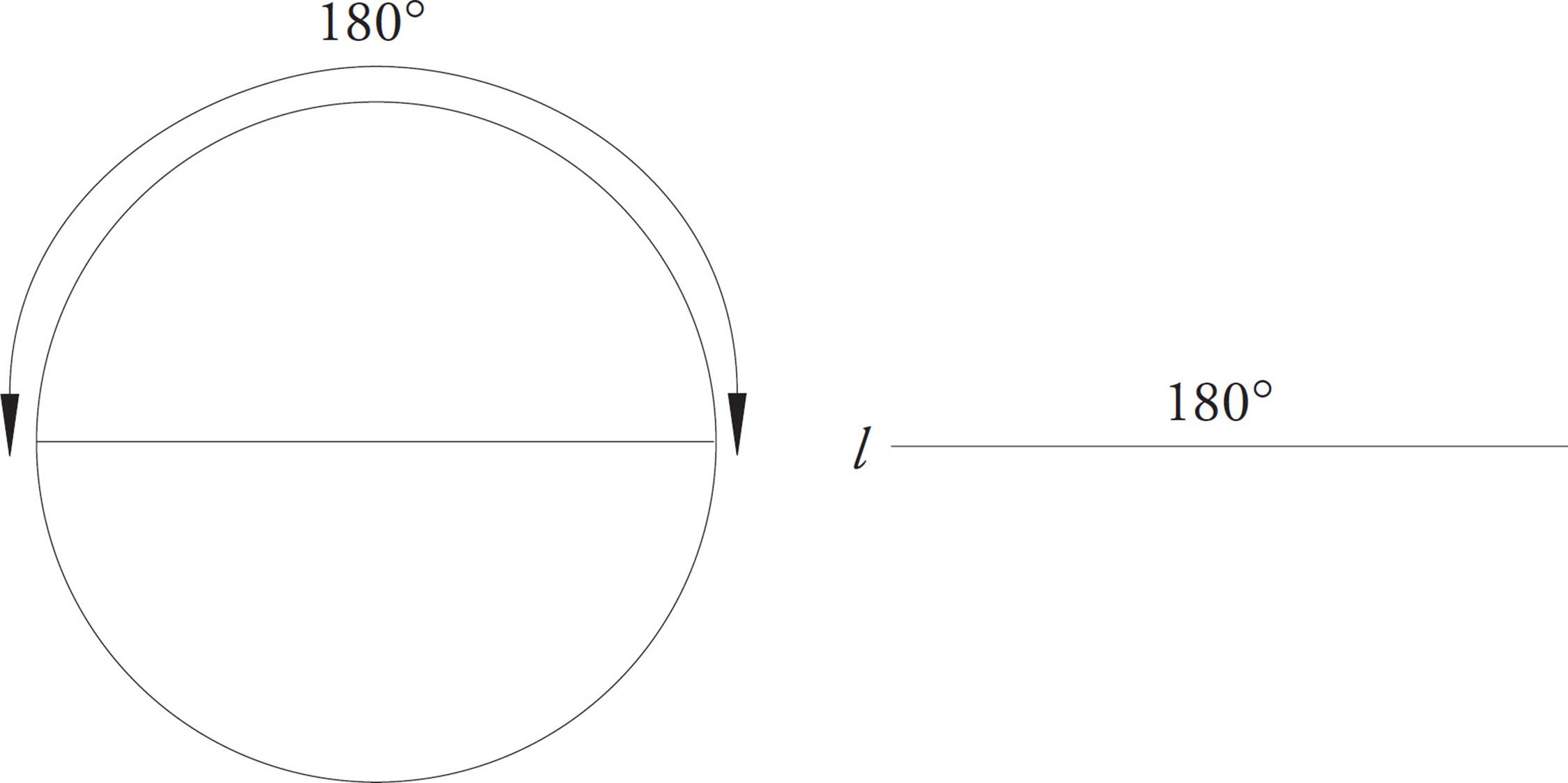
3.A line is a 180-degree angle.
You probably don’t think of a line as an angle, but it is one. Think of it as a flat angle. The following drawings should help:
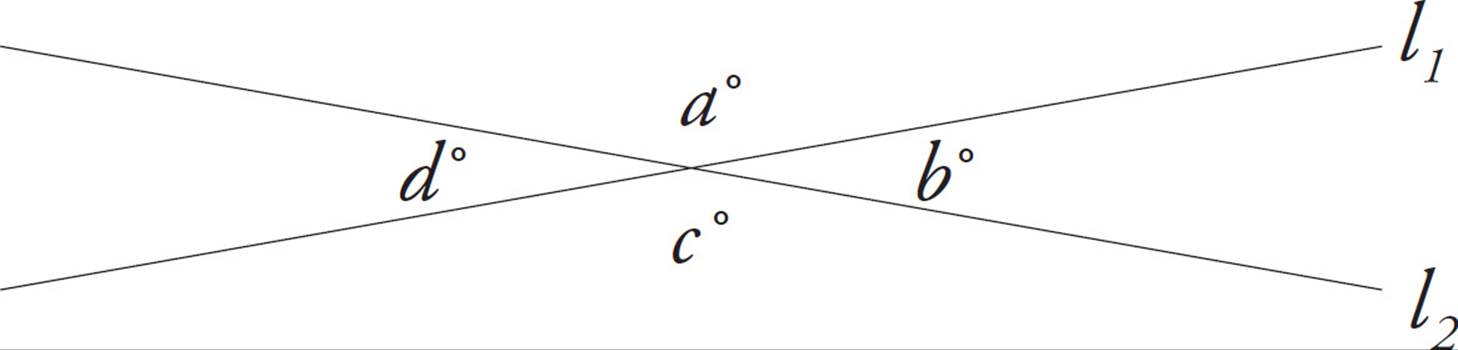
4.When two lines intersect, four angles are formed.
The following diagram should make this clear. The four angles are indicated by letters.
5.When two lines intersect, the angles opposite each other will have the same measures.
Such angles are called vertical angles. In the following diagram, angles a and c are equal; so are angles b and d.
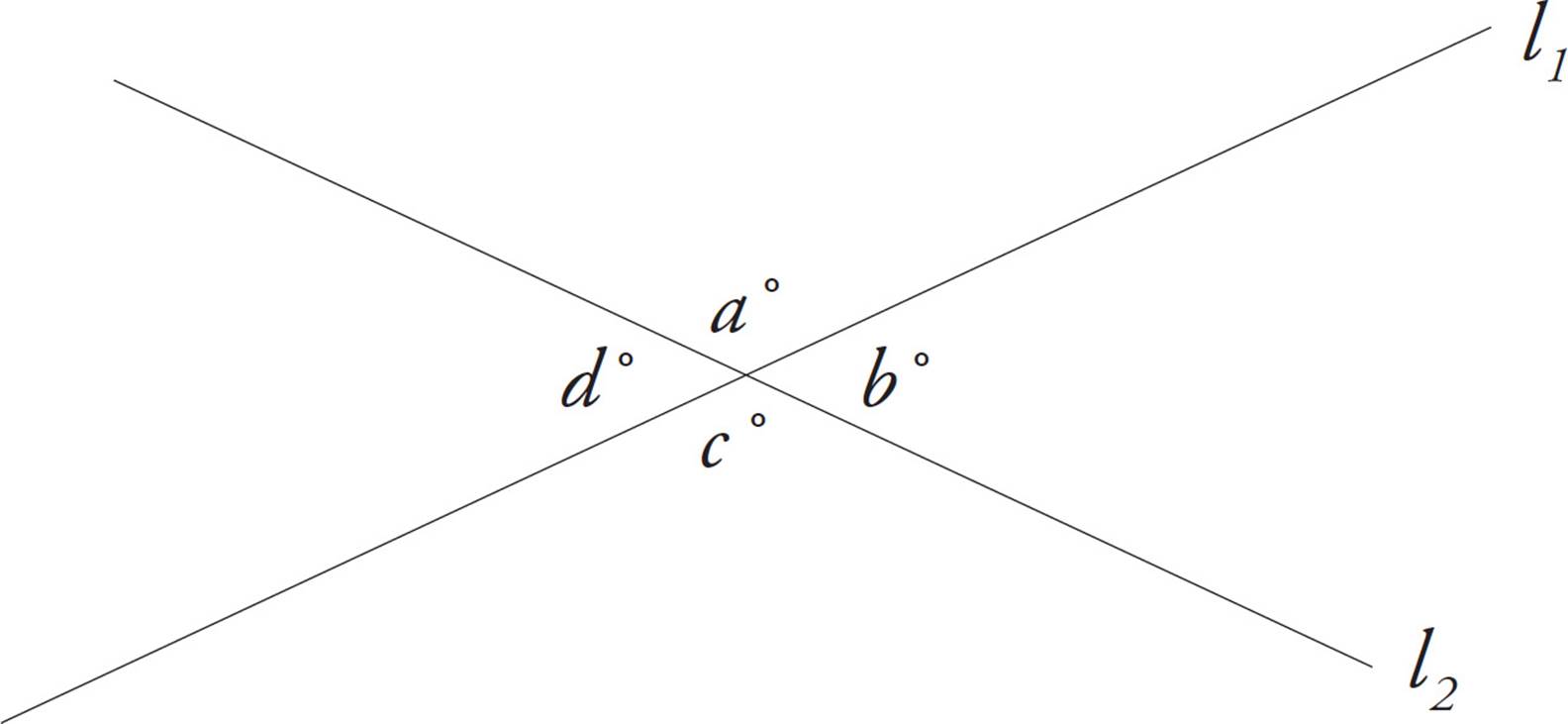
a + b + c + d = 360°
a = c, b = d
The measures of these four angles add up to 360 degrees. (Remember the circle.)
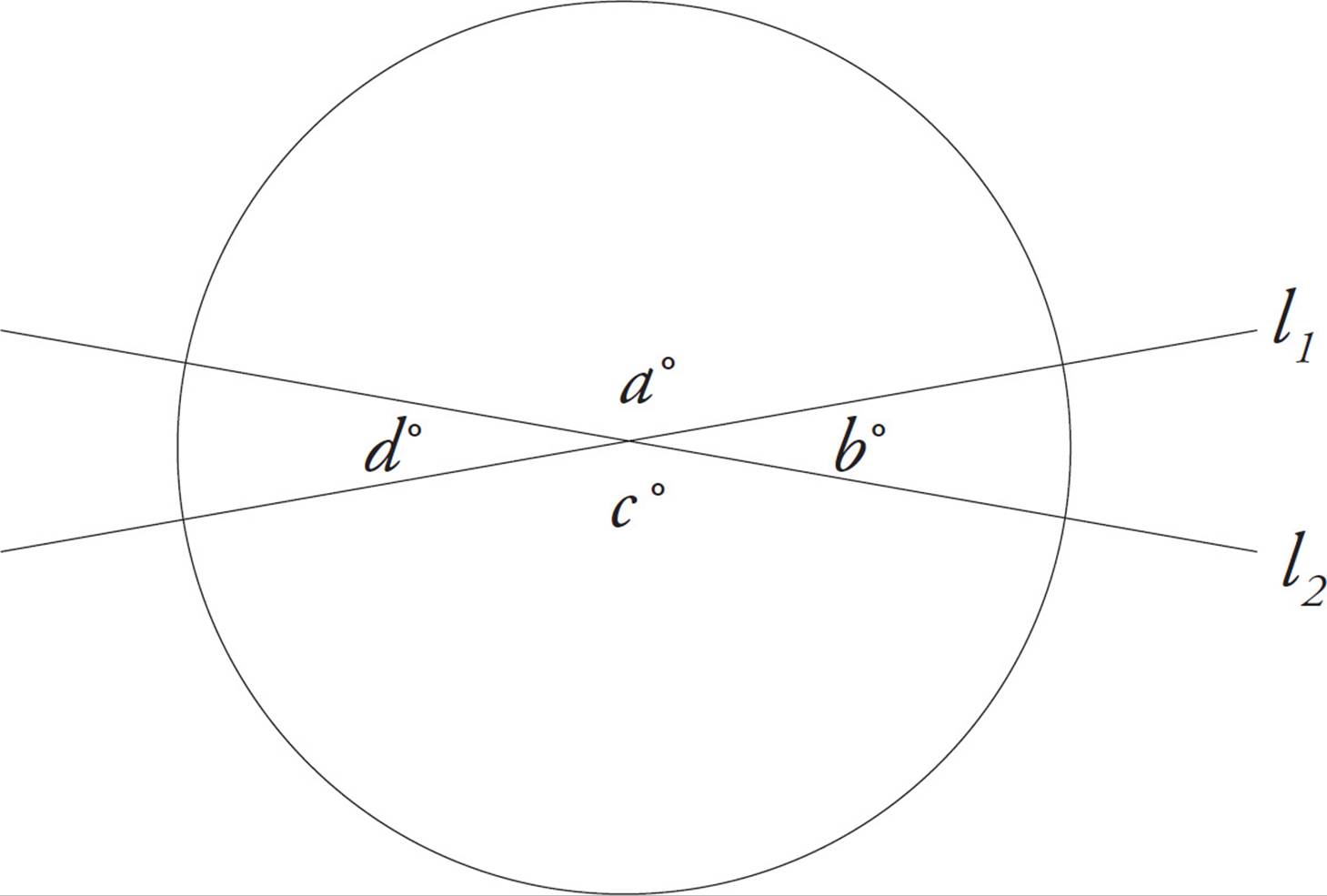
a + b + c + d = 360°
It doesn’t matter how many lines you intersect through a single point. The total measure of all the angles formed will still be 360 degrees.
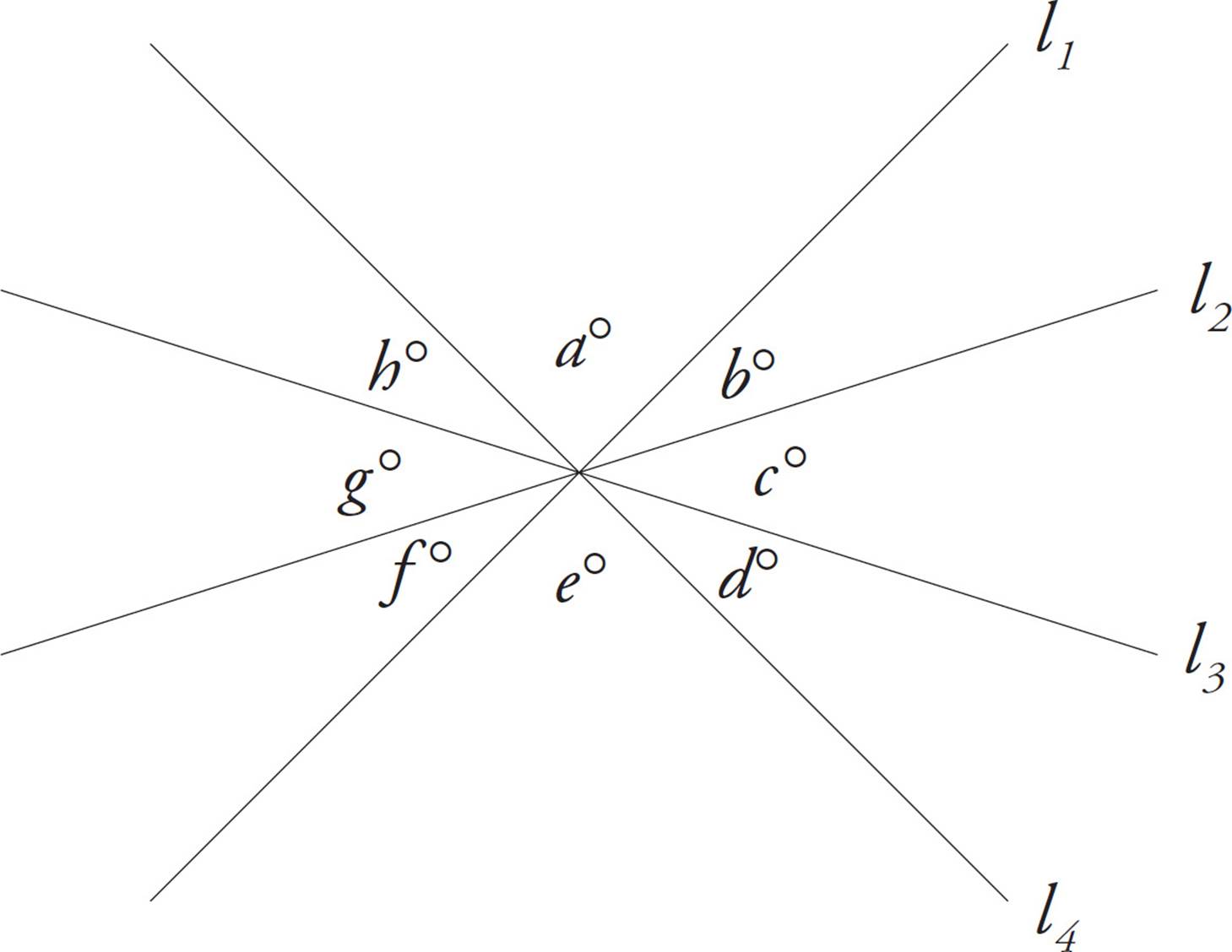
a + b + c + d + e + f + g + h = 360°
a = e, b = f, c = g, d = h
6.If two lines are perpendicular to each other, each of the four angles formed is 90 degrees. A 90-degree angle is called a right angle.
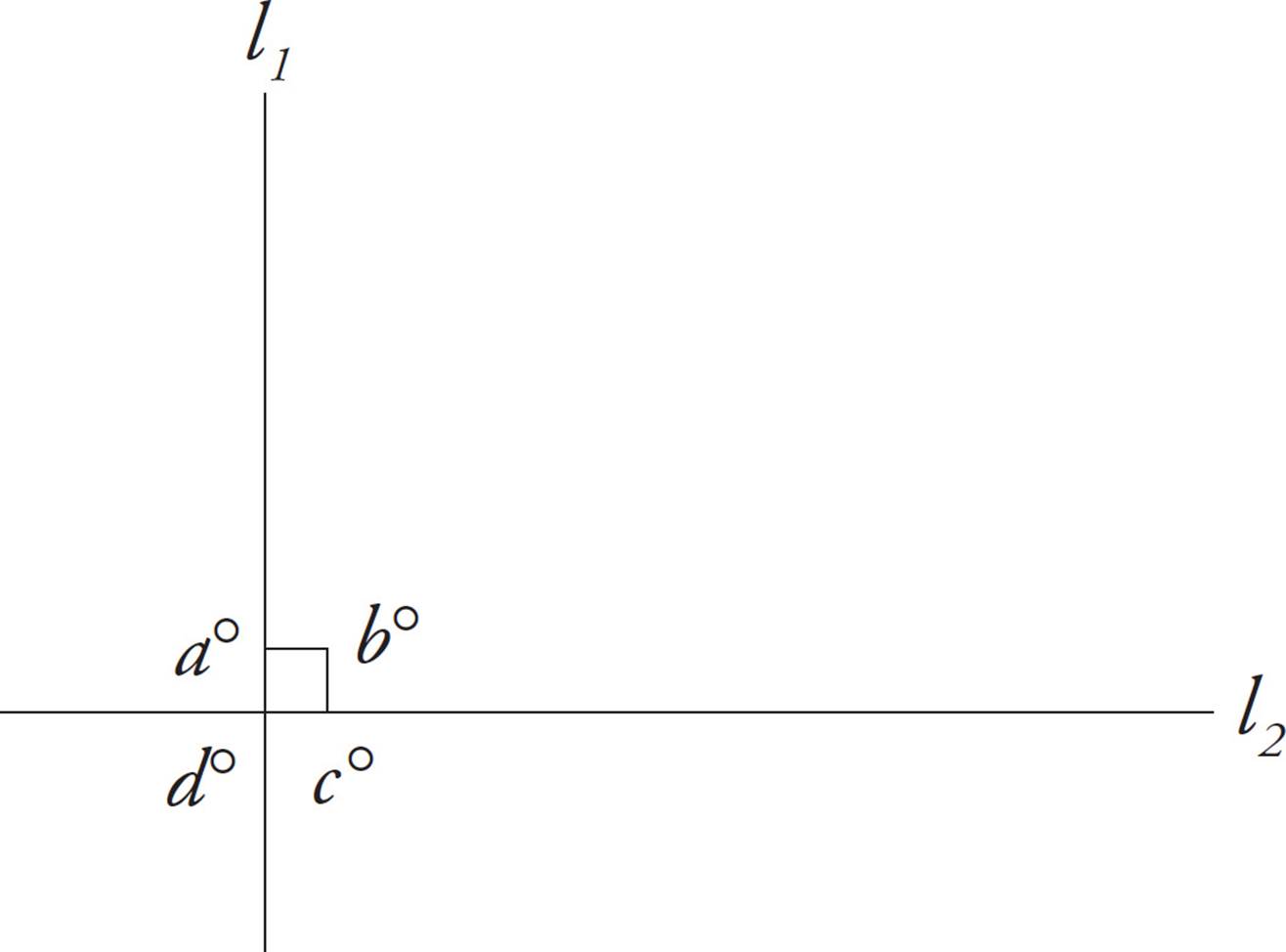
Angles a, b, c, and d all equal 90 degrees.
Perpendicular:
Meeting at right
(90°) angles
The little box at the intersection of the two lines is the symbol for a right angle. If the lines are not perpendicular to each other, then none of the angles will be right angles. Don’t assume that an angle is a right angle unless you are specifically told that it is a right angle, either in the problem or with the 90° symbol.
Flip and Negate
If two lines are perpendicular,
then their slopes
are negative reciprocals;
i.e., if l1 has a slope of
2 and l2 is perpendicular
to l1, then l2 must have a
slope of −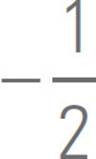 .
.
7.When two parallel lines are cut by a third line, all of the small angles are equal, all of the big angles are equal, and the sum of any big angle and any small angle is 180 degrees.
Parallel lines are two lines that never intersect, and the rules about parallel lines are usually taught in school with lots of big words. But we like to avoid big words whenever possible. Simply put, when a line cuts through two parallel lines, two kinds of angles are created: big angles and small angles. You can tell which angles are big and which are small just by looking at them. All the big angles look equal, and they are. The same is true of the small angles. Lastly, any big angle plus any small angle always equals 180 degrees. (ETS likes rules about angles that add up to 180 or 360 degrees.)
Parallel Lines
Parallel lines have
the same slope.
In any geometry problem, never assume that two lines are parallel unless the question or diagram specifically tells you so. In the following diagram, angle a is a big angle, and it has the same measure as angles c, e, and g, which are also big angles. Angle b is a small angle, and it has the same measure as angles d, f, and h, which are also small angles.
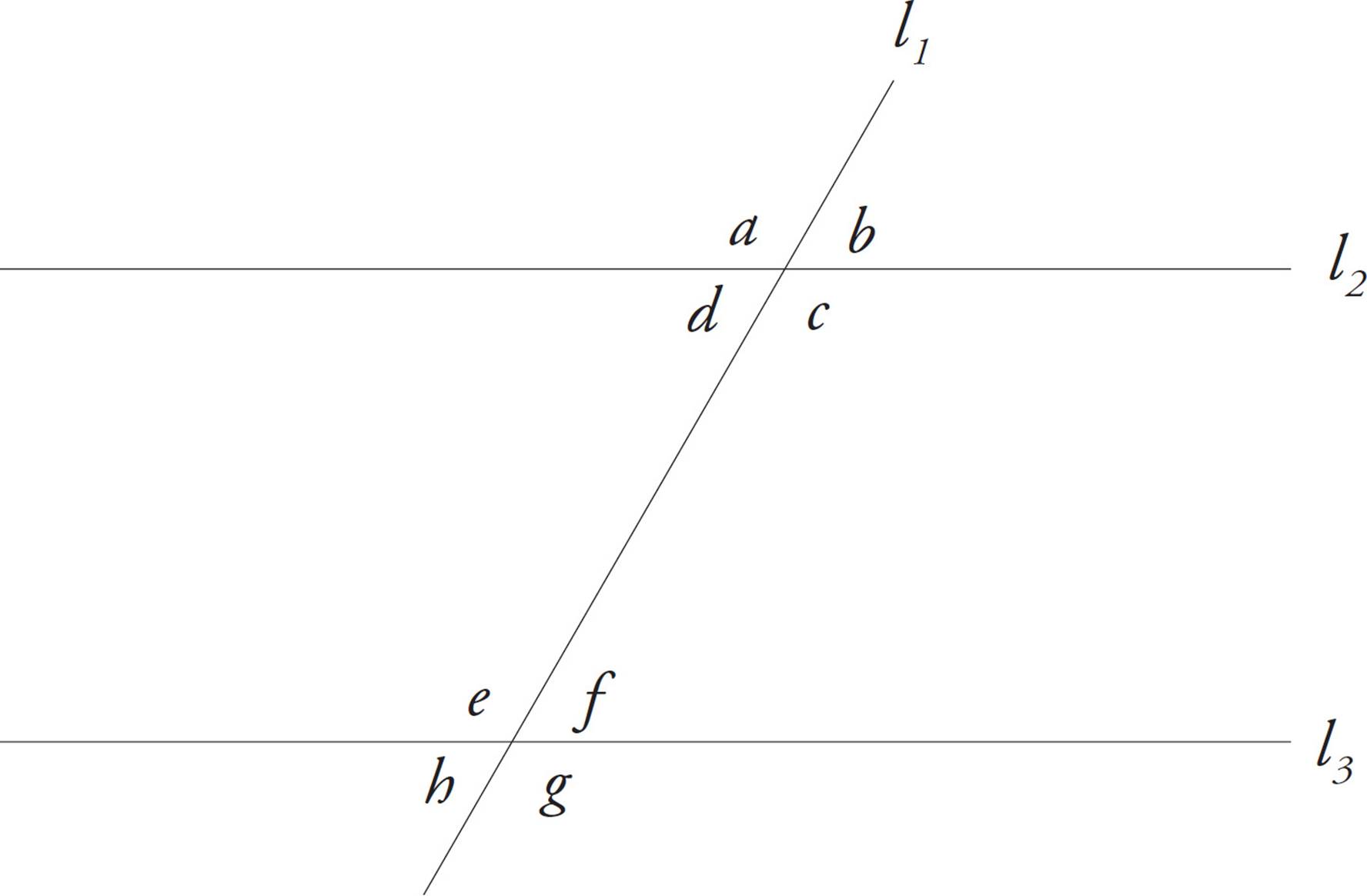
a = c = e = g
b = d = f = h
l2 = l3
You should be able to see that the degree measures of angles a, b, c, and d add up to 360 degrees. So do those of angles e, f, g, and h. If you have trouble seeing it, draw a circle around the angles. What is the degree measure of a circle? Also, the sum of any small angle (such as d) and any big angle (such as g) is 180°.
Let’s see how these concepts might be tested on the SAT.
![]()
12.
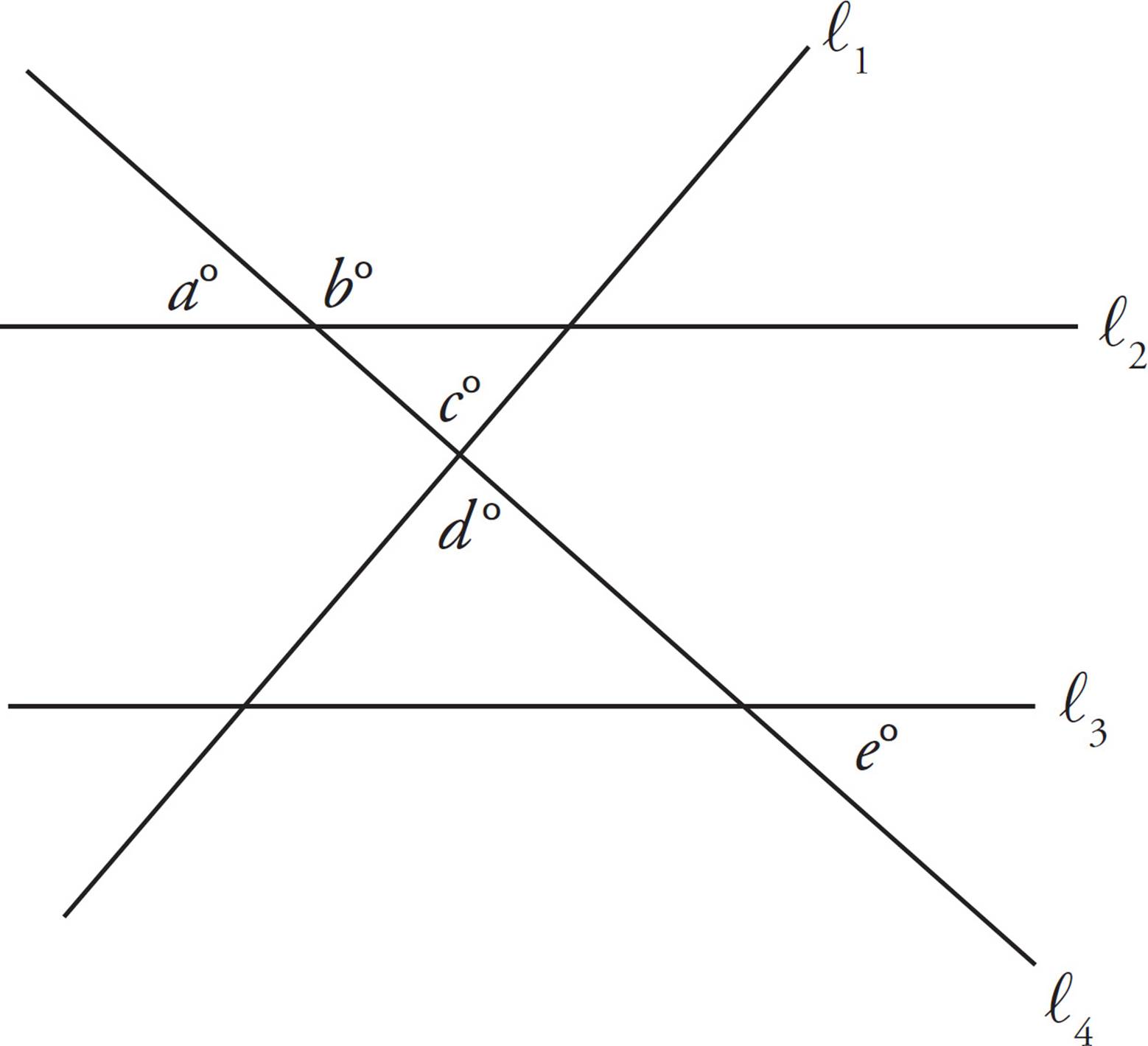
Note: Figure not drawn to scale.
In the figure above, l2 || l3. Which of the following could be false?
A)a = e
B)b + e = 180
C)l1 ⊥ l4
D)c = d
Here’s How to Crack It
Start by marking l2 and l3 as parallel lines. Next, because you’re looking for what could be false, consider each answer choice and use POE. For (A), if l2 and l3 are parallel, then l4 transects both lines and creates sets of equal angles. All small angles around l4 which are formed by l2 or l3 are equal, so a must be equal to e; eliminate (A). Choice (B) is based on the same set of intersecting lines; because l2 and l3 are parallel and l4 transects both lines, then any big angle plus any small angle equals 180°. Therefore, (B) must be true; eliminate it. For (C), you don’t know the value of any angles, so you cannot determine if these lines are perpendicular. Since (C) could be false, choose (C). Choice (D) must be true because opposite angles created by two lines are always equal.
![]()
Converting Degrees to Radians
Some geometry questions will ask you to convert an angle measurement from degrees to radians. While this may sound scary, doing this conversion requires only that you remember that 180 degrees = π radians. Use this relationship to set up a proportion (see Chapter 14) and convert the units.
![]()

27.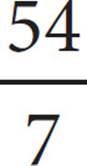 π radians is approximately equal to how many degrees?
π radians is approximately equal to how many degrees?
A)8°
B)694°
C)1,389°
D)2,777°
Here’s How to Crack It
Use the relationship between radians and degrees to set up a proportion. If 180 degrees = π radians, then the proportion will look like the following:
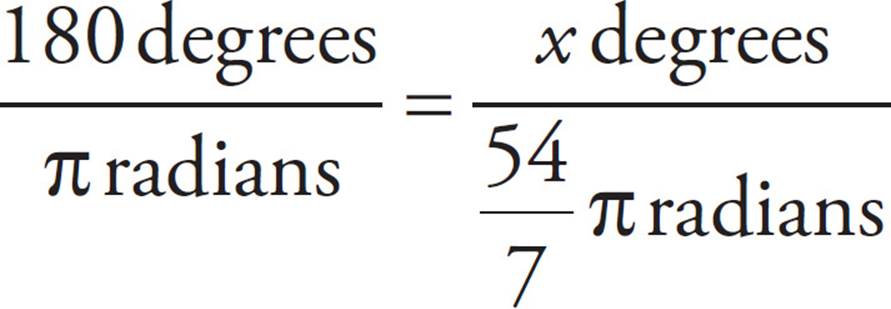
Cross-multiply to get 180 × 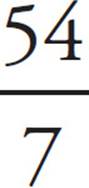 π = πx. Divide both sides by π : 180 ×
π = πx. Divide both sides by π : 180 × 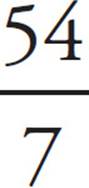 = x. Finally, use your calculator, and you find that x is approximately 1,389, which is (C).
= x. Finally, use your calculator, and you find that x is approximately 1,389, which is (C).
![]()
Triangles
Here are some basic triangle rules you’ll need to know for the SAT.
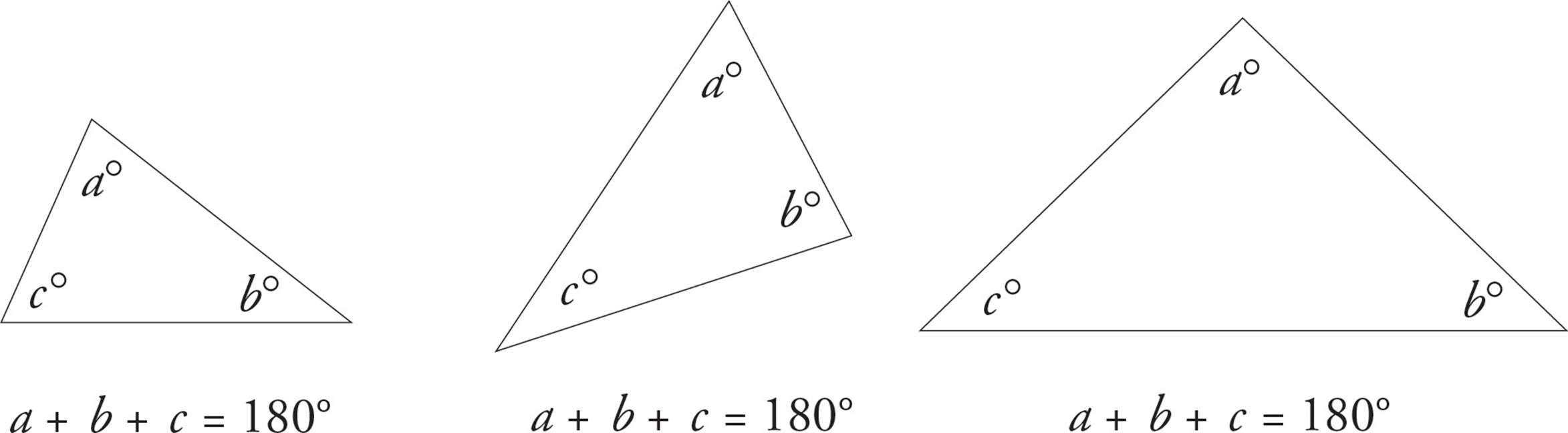
1.Every triangle contains 180 degrees.
The word triangle means “three angles,” and every triangle contains three interior angles. The measure of these three angles always adds up to exactly 180 degrees. You don’t need to know why this is true or how to prove it. You just need to know it. And we mean know it.
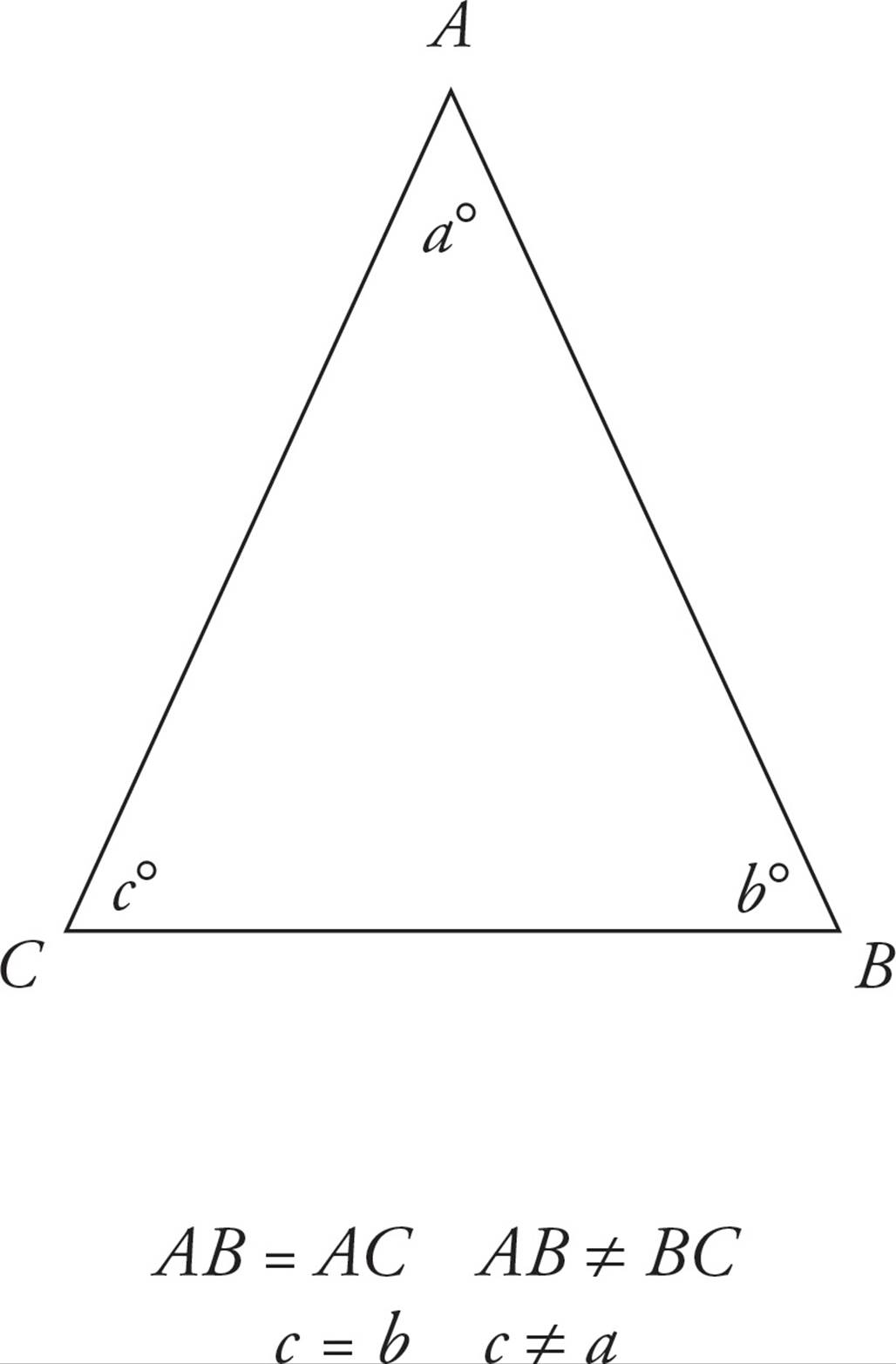
2.An isosceles triangle is one in which two of the sides are equal in length.
The angles opposite those equal sides are also equal because angles opposite equal sides are also equal.

Your Friend the Triangle
If ever you are stumped by
a geometry problem that
deals with a quadrilateral,
hexagon, or other polygon,
look for the triangles that
you can form by drawing
lines through the figure.
3.An equilateral triangle is one in which all three sides are equal in length.
Because the angles opposite equal sides are also equal, all three angles in an equilateral triangle are equal too. (Their measures are always 60 degrees each.)
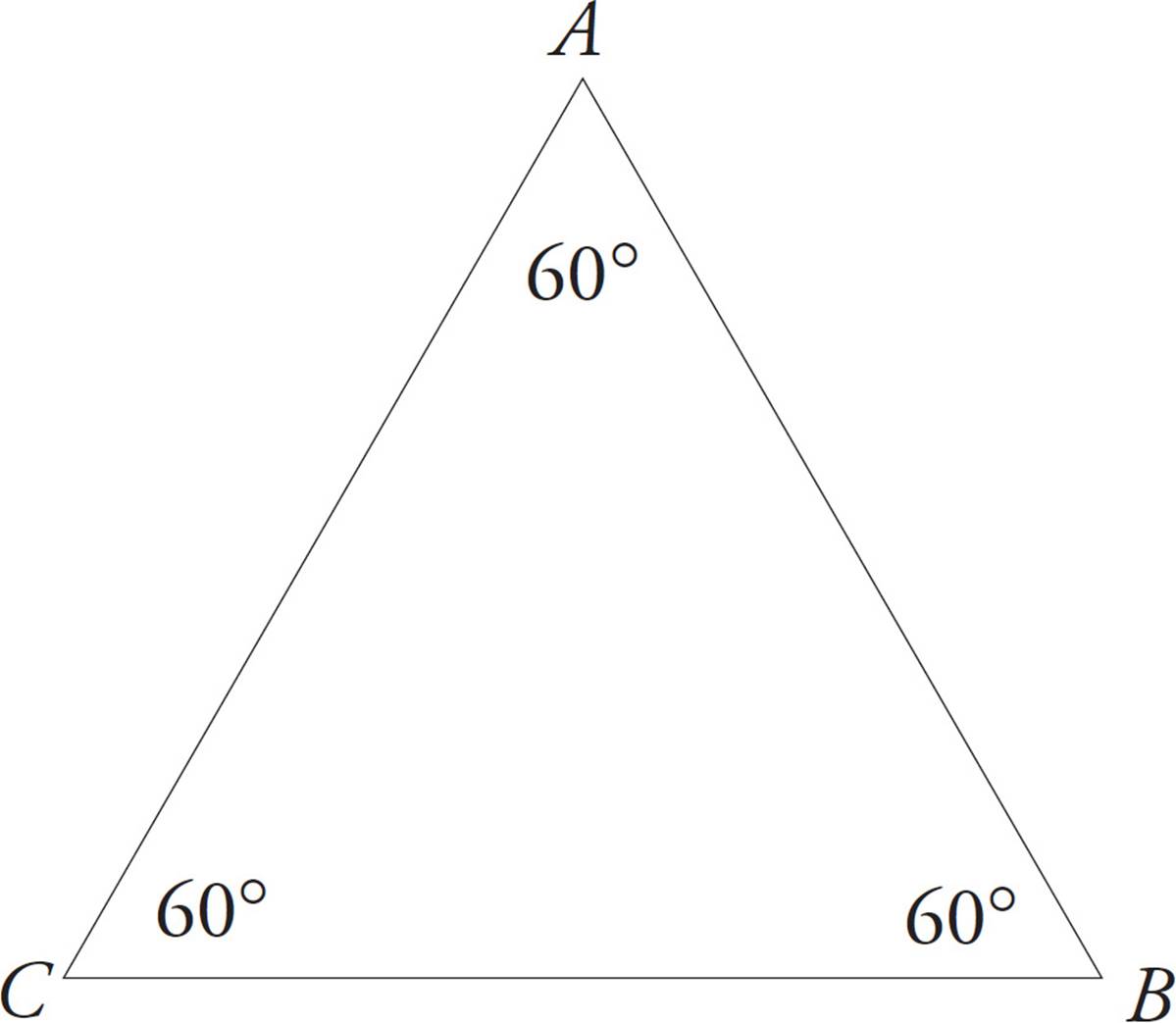
AB = BC = AC
Equilateral Triangles
An equilateral triangle
is also isoceles.
4.A right triangle is a triangle in which one of the angles is a right angle (90 degrees).
The longest side of a right triangle, which is always opposite the 90-degree angle, is called the hypotenuse.
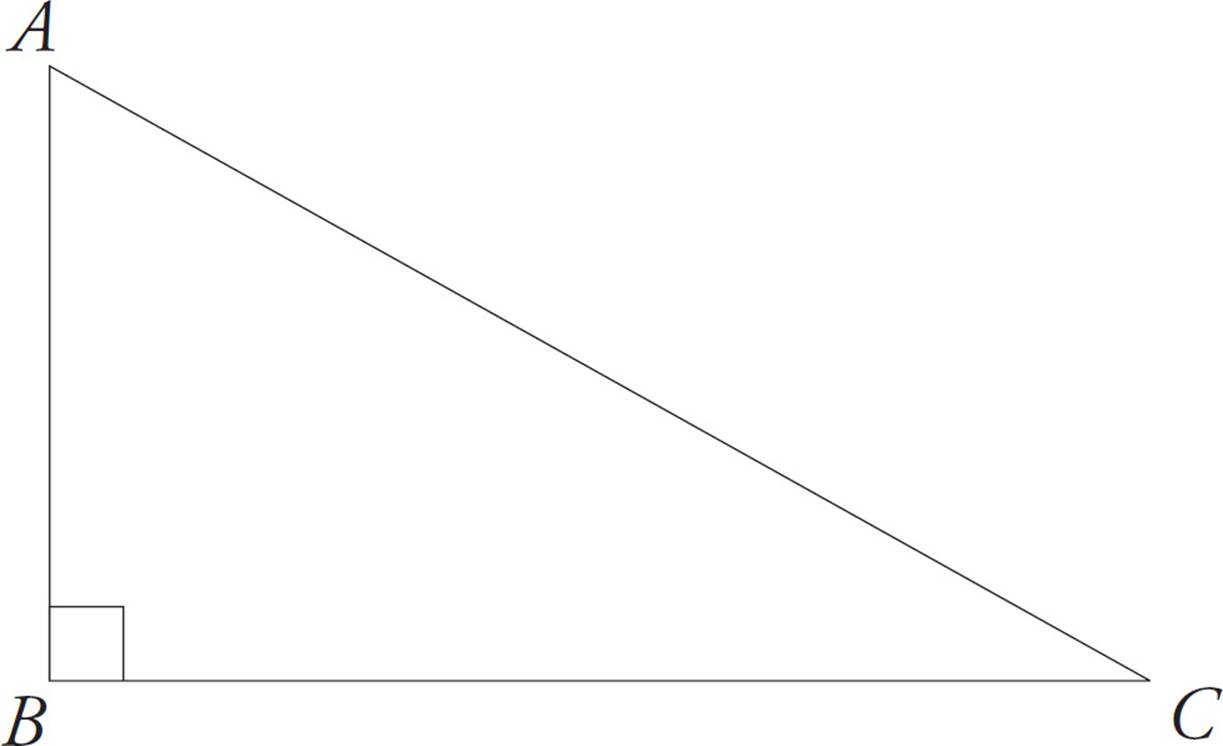
AC is the hypotenuse.
Some right triangles are also isosceles. The angles in an isosceles right triangle always measure 45°, 45°, and 90°.
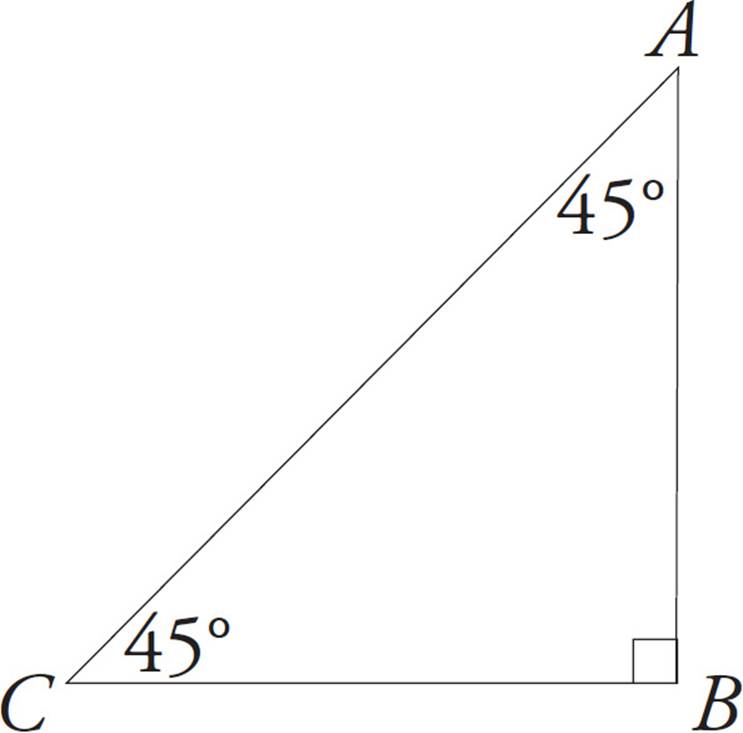
AB = BC
5.The perimeter of a triangle is the sum of the lengths of its sides.
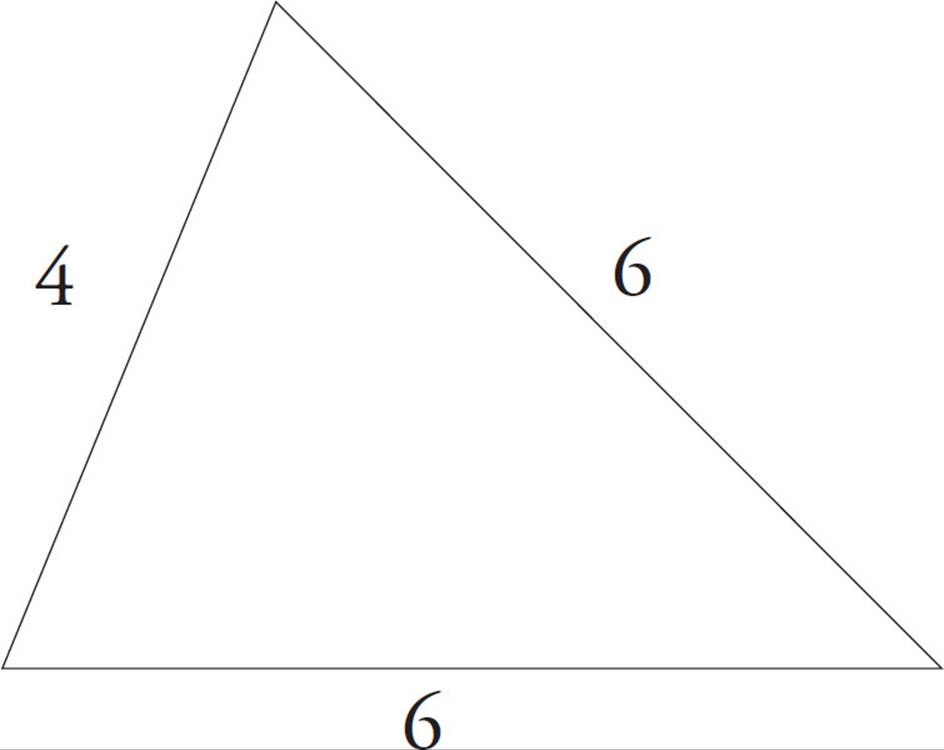
perimeter = 4 + 6 + 6 = 16
6.The area of a triangle is ![]() (base × height).
(base × height).
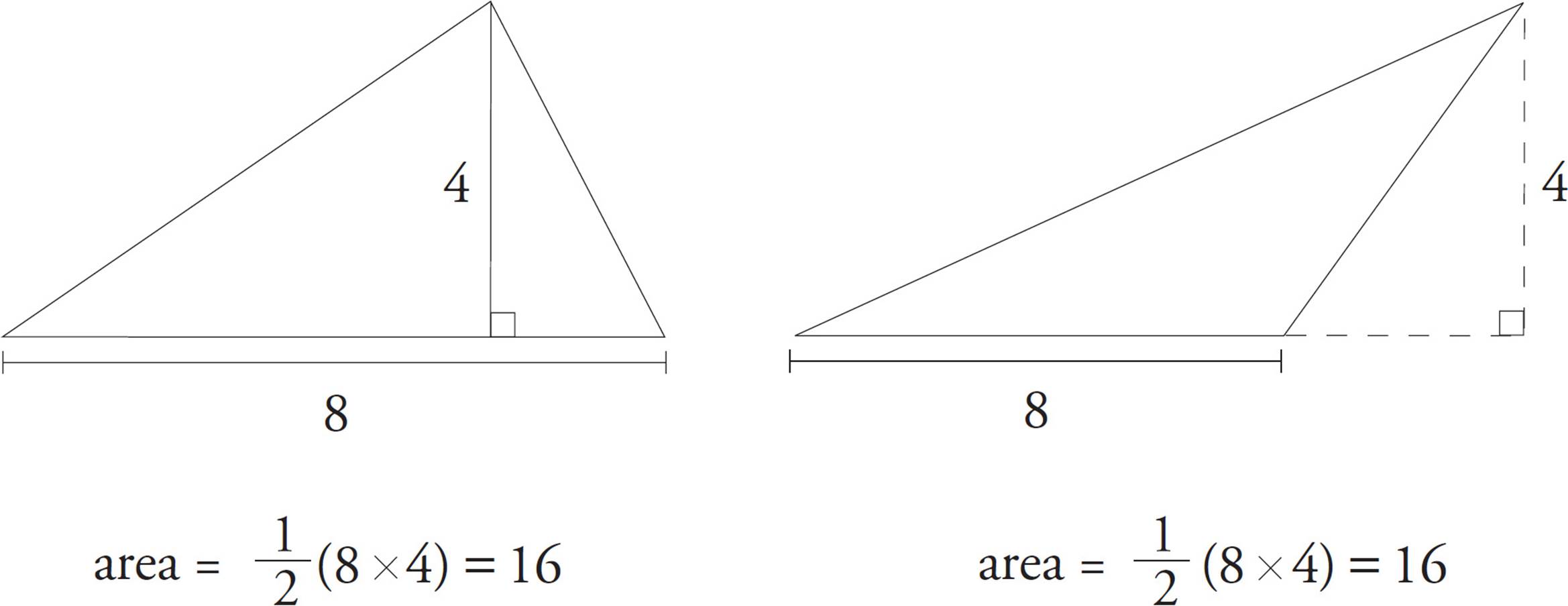
In or Out
The height can be found
with a line dropped inside
or outside the triangle—
just as long as it’s
perpendicular to the base.
Try a question testing some of these concepts:
![]()
3.
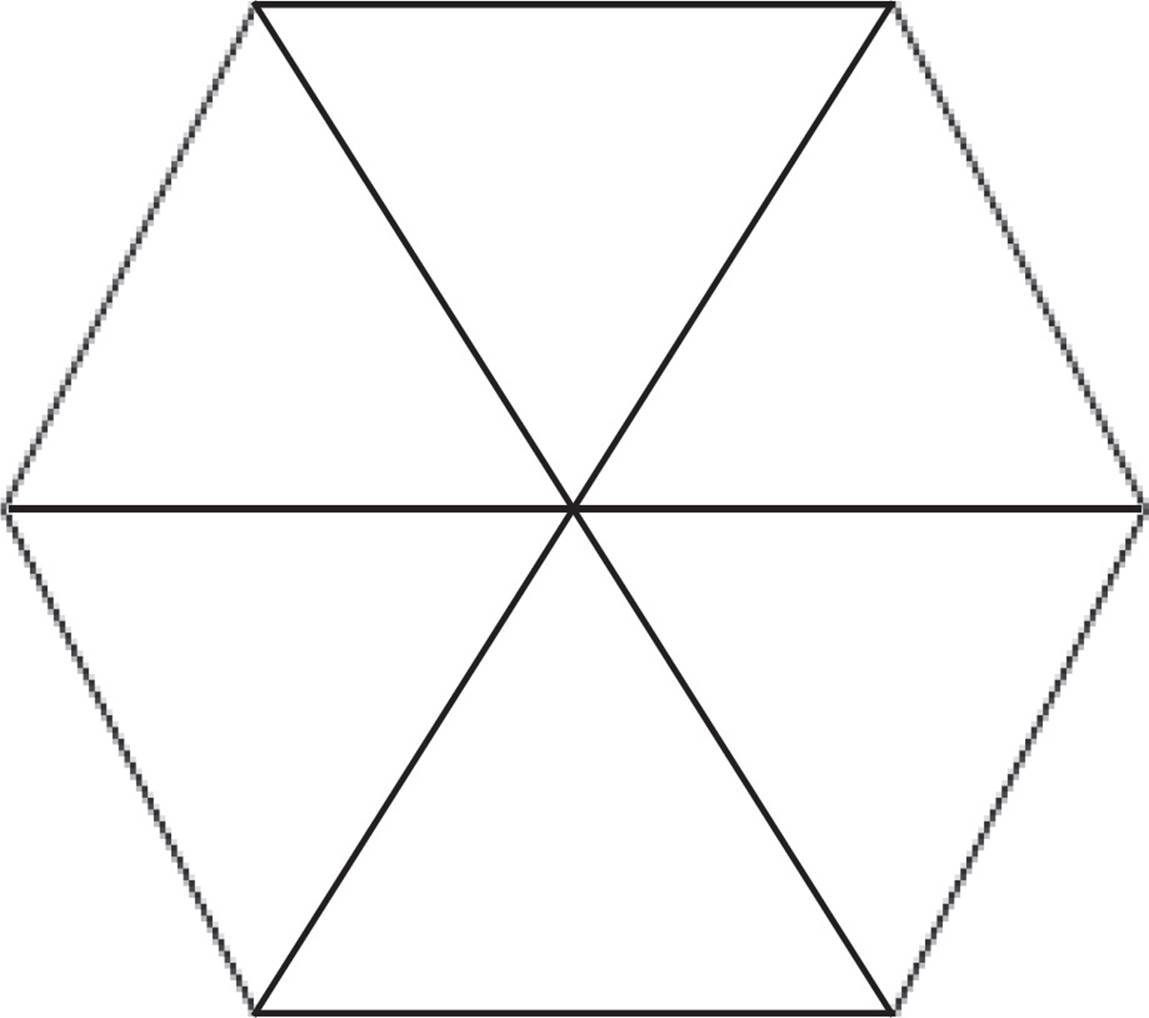
The regular hexagon shown above is divided into six congruent equilateral triangles. What is the measure, in degrees, of one of the interior angles of the hexagon?
A)60°
B)120°
C)180°
D)360°
Here’s How to Crack It
First, you can Ballpark and eliminate (C) and (D); (C) would be a straight line, and (D) is all the way around a circle, so neither of those can be the interior angle of this figure. Next, label what you know. If each of the triangles in the figure is equilateral, then all of the angles within the triangles are equal to 60°. The interior angles of the hexagon are comprised of two angles of the triangles, so the interior angles of the hexagon must be 2 × 60 = 120°, which is (B).
![]()
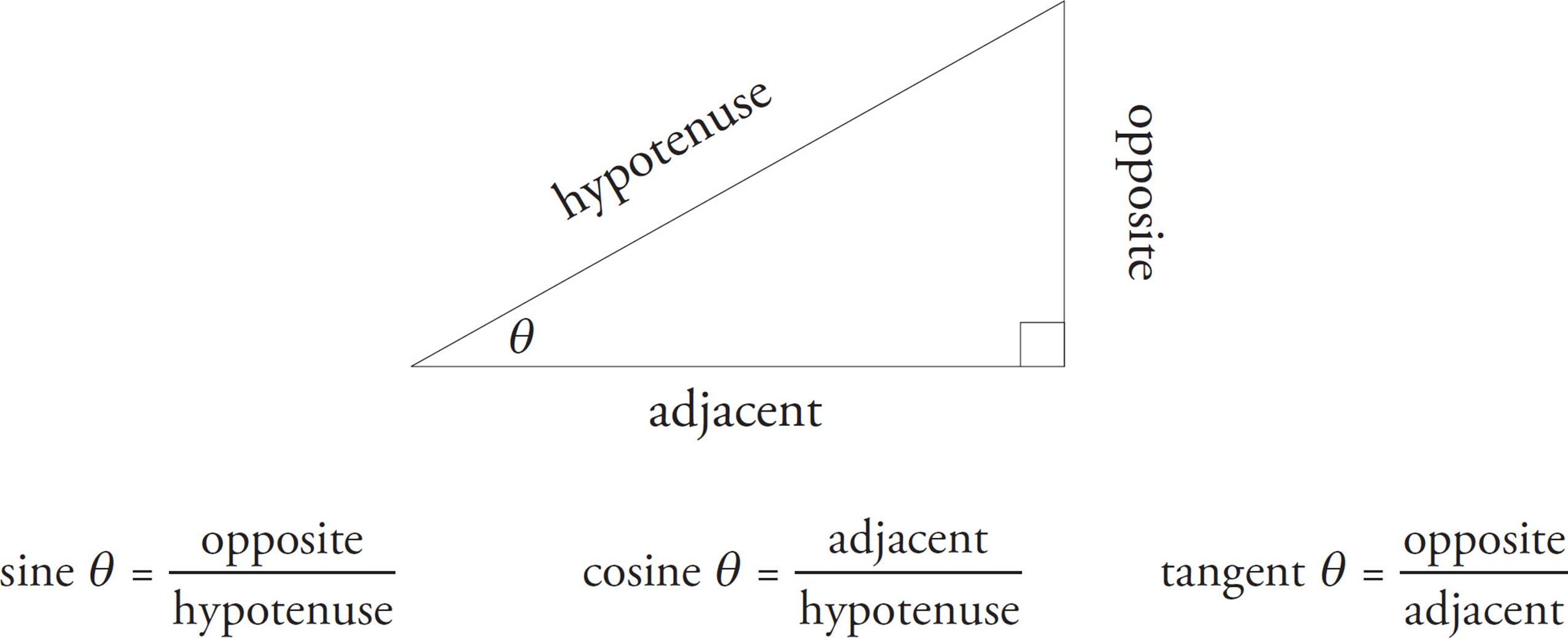
SOHCAHTOA
Trigonometry will likely appear on your SAT. But fear not! Many trigonometry questions you will see mostly require you to know the basic definitions of the three main trigonometric functions. SOHCAHTOA is a way to remember the three functions:
Let’s see an example:
![]()
11.
In the triangle above, sin x = 0.8 and cos x = 0.6. What is the area of the triangle?
A)0.48
B)4.8
C)24
D)48
Here’s How to Crack It
Use the definitions of sine and cosine to find the two legs of the triangle. Sine is 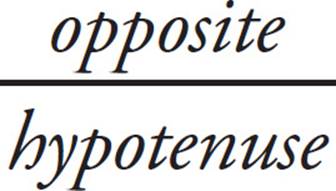 , so if sin x = 0.8, then 0.8 =
, so if sin x = 0.8, then 0.8 = 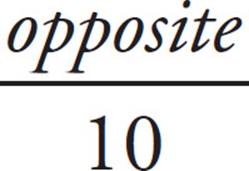 . Multiply both sides by 10 and you find the side opposite the angle with measure x° is 8. Similarly, cosine is
. Multiply both sides by 10 and you find the side opposite the angle with measure x° is 8. Similarly, cosine is 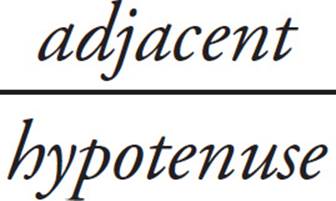 , so if cos x = 0.6, then 0.6 =
, so if cos x = 0.6, then 0.6 = 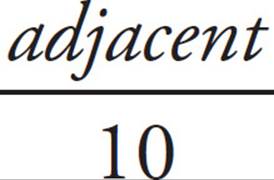 . Multiply both sides by 10 to determine the side adjacent to the angle with measure x° is 6. With those two sides, find the area. The formula for area is A =
. Multiply both sides by 10 to determine the side adjacent to the angle with measure x° is 6. With those two sides, find the area. The formula for area is A = ![]() bh, so A =
bh, so A = ![]() (6)(8) = 24, which is (C).
(6)(8) = 24, which is (C).
![]()
Pythagorean Theorem
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. As we told you earlier, the hypotenuse is the longest side of a right triangle; it’s the side opposite the right angle. The square of the hypotenuse is its length squared. Applying the Pythagorean theorem to the following drawing, we find that c2 = a2 + b2.
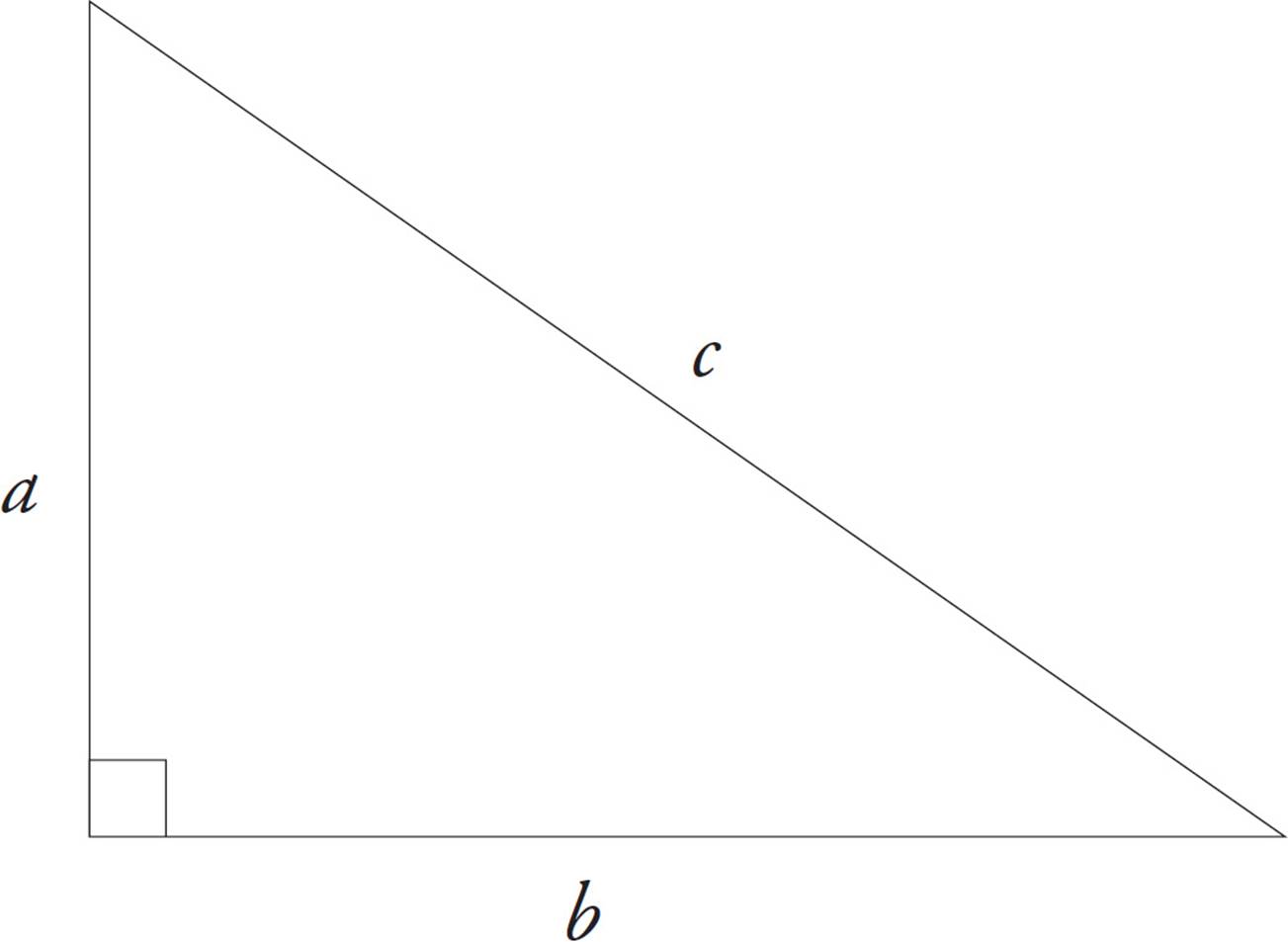
Pythagorean Theorem
a2 + b2 = c2, where c is
the hypotenuse of a right
triangle. Learn it; love it.
If you forget the Pythagorean theorem, you can always look it up in the box at the beginning of the Math sections.
ETS loves to test the Pythagorean theorem along with SOHCAHTOA:
![]()
15.In ΔABC (not shown), AC ⊥ BC and cos ∠ABC = 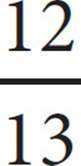 . What is the value of tan ∠ABC ?
. What is the value of tan ∠ABC ?
A)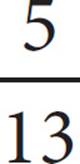
B)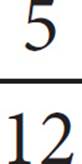
C)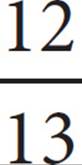
D)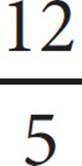
Here’s How to Crack It
Start by drawing triangle ABC.
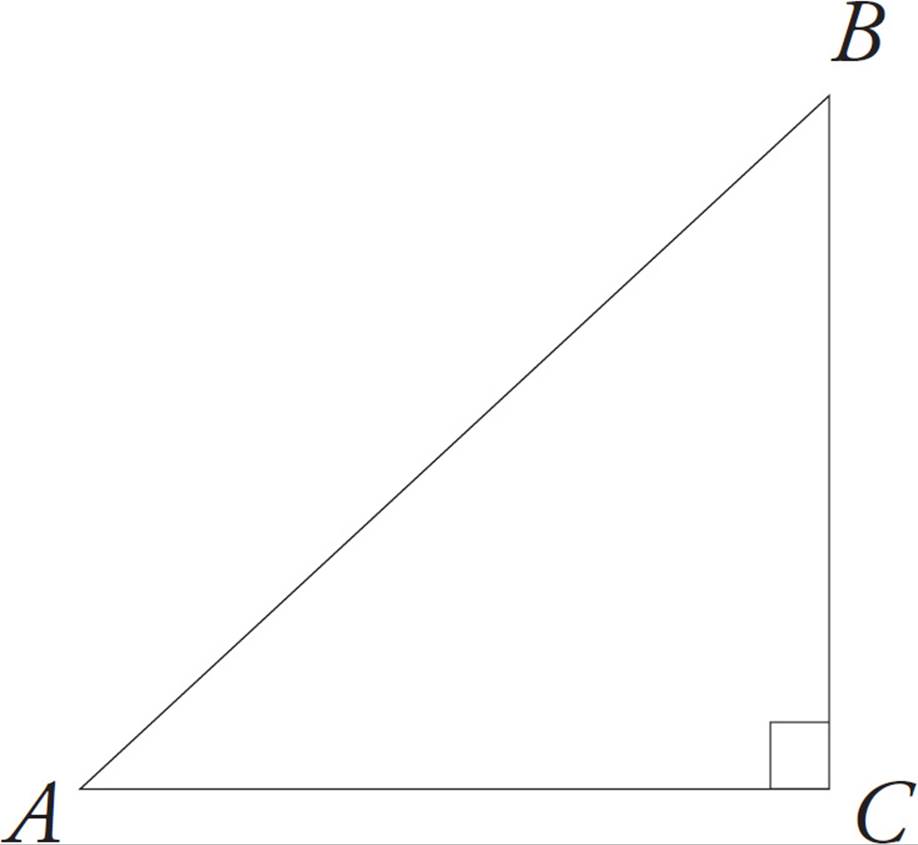
Next, label what you can. You don’t know the actual side lengths, but because cos ∠ABC = 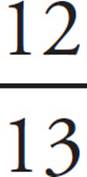 , you do know the relationship between the side adjacent to angle ABC and the hypotenuse. You can plug in for this relationship: Make BC (the side adjacent to the angle) 12 and AB (the hypotenuse) 13:
, you do know the relationship between the side adjacent to angle ABC and the hypotenuse. You can plug in for this relationship: Make BC (the side adjacent to the angle) 12 and AB (the hypotenuse) 13:
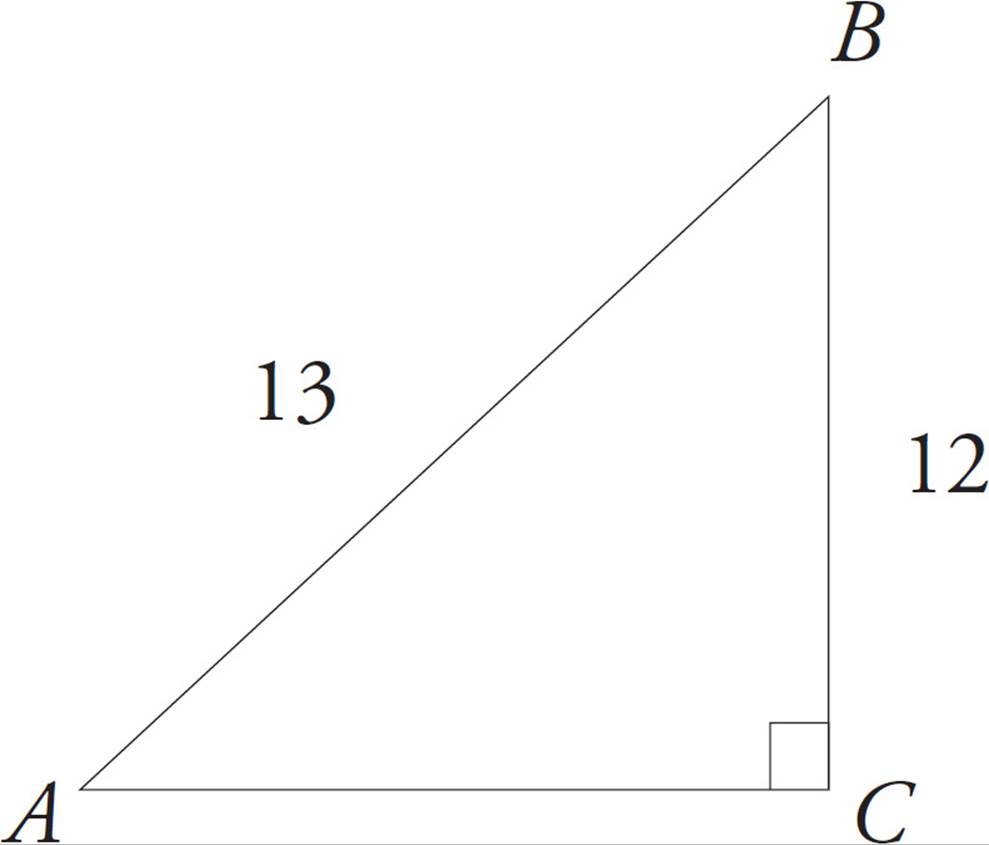
You need to find tan ∠ABC, which means you need 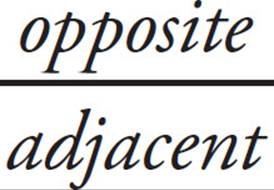 . You already know the adjacent side is 12, but you still need the side opposite, AC. Use the Pythagorean theorem to find the missing side:
. You already know the adjacent side is 12, but you still need the side opposite, AC. Use the Pythagorean theorem to find the missing side:
a2 + b2 = c2
122 + b2 = 132
144 + b2 = 169
b2 = 25
b = 5
Therefore, AC = 5, and tan ∠ABC = 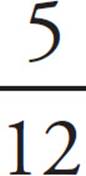 , which is (B).
, which is (B).
![]()
Special Right Triangles
Both of the previous questions you worked also used special right triangles. While in the last question we used the Pythagorean theorem to find the missing side, if you memorize these special triangles you can avoid using the Pythagorean theorem in a lot of cases.
Your Friend
the Rectangle
Be on the lookout for
problems in which the
application of the
Pythagorean theorem is
not obvious. For example,
every rectangle contains
two right triangles.
That means that if you
know the length
and width of the rectangle,
you also know the length
of the diagonal, which
is the hypotenuse of
both triangles.
ETS writes very predictable geometry questions involving right triangles, reusing certain relationships. In these questions the triangles being used have particular ratios. There are two different types of special right triangles. The first involves the ratio of sides and the second involves the ratio of angles.
The most common special right triangles with side ratios are known as Pythagorean triplets. Here are ETS’s favorites:
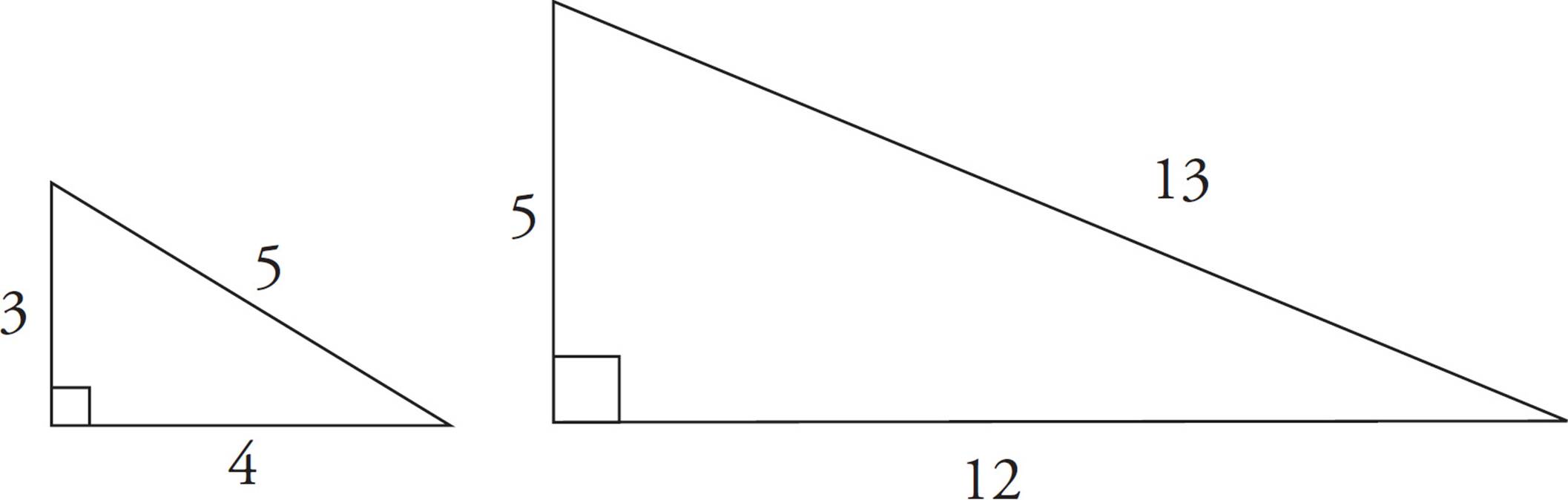
If you memorize these two sets of Pythagorean triplets (3-4-5 and 5-12-13), you’ll often be able to find ETS’s answer without using the Pythagorean theorem. If ETS gives you a triangle with a side of 3 and a hypotenuse of 5, you know right away that the other side has to be 4. Likewise, if you see a right triangle with sides of 5 and 12, you know the hypotenuse must be 13.
Relax; It’s Just a Ratio
A 3-4-5 triangle may be
hiding, disguised as 6-8-10
or 18-24-30. It’s all the
same ratio though, so be
on the lookout.
ETS also likes to use right triangles with sides that are simply multiples of the common Pythagorean triplets. For example, you might see a 6-8-10 or a 10-24-26 triangle. These sides are simply the sides of the 3-4-5 and 5-12-13 triangles multiplied by 2.
There are two types of special right triangles that have a specific ratio of angles. They are the 30°-60°-90° triangle and the 45°-45°-90° triangle. The sides of these triangles always have the same fixed ratio to each other. The ratios are as follows:
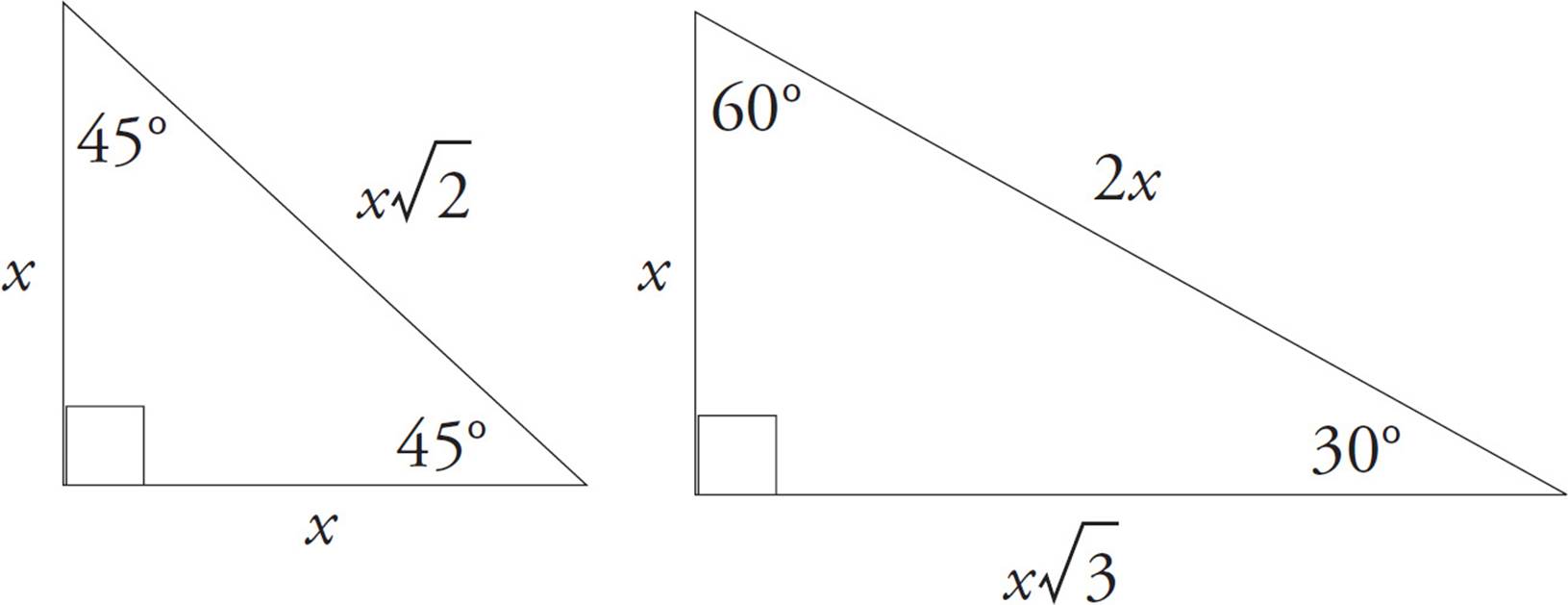
Let’s talk about a 45°-45°-90° triangle first. Did you notice that this is also an isosceles right triangle? The sides will always be the same. And the hypotenuse will always be the side times 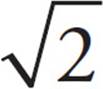 . Its ratio of side to side to hypotenuse is always 1:1:
. Its ratio of side to side to hypotenuse is always 1:1: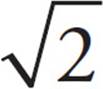 . For example, if you have a 45°-45°-90° triangle with a side of 3, then the second side will also be 3 and the hypotenuse will be 3
. For example, if you have a 45°-45°-90° triangle with a side of 3, then the second side will also be 3 and the hypotenuse will be 3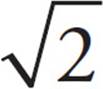 .
.
Now let’s talk about a 30°-60°-90° triangle. The ratio of shorter side to longer side to hypotenuse is always 1: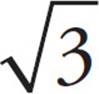 :2. For example, if the shorter side of a 30°-60°-90° triangle is 5, then the longer side would be 5
:2. For example, if the shorter side of a 30°-60°-90° triangle is 5, then the longer side would be 5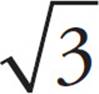 and the hypotenuse would be 10.
and the hypotenuse would be 10.
Symbols
Things aren’t always written out on the SAT. Here’s a list of symbols you might see, along with a translation of each one into English:
|
Symbol |
Meaning |
|
∆ABC |
triangle ABC |
|
|
line segment AB |
|
AB |
the length of line segment AB |
Learn these symbols and keep an eye out for them!
Similar Triangles
Similar triangles have the same shape, but they are not necessarily the same size. Having the same shape means that the angles of the triangles are identical and that the corresponding sides have the same ratio. Look at the following two similar triangles:
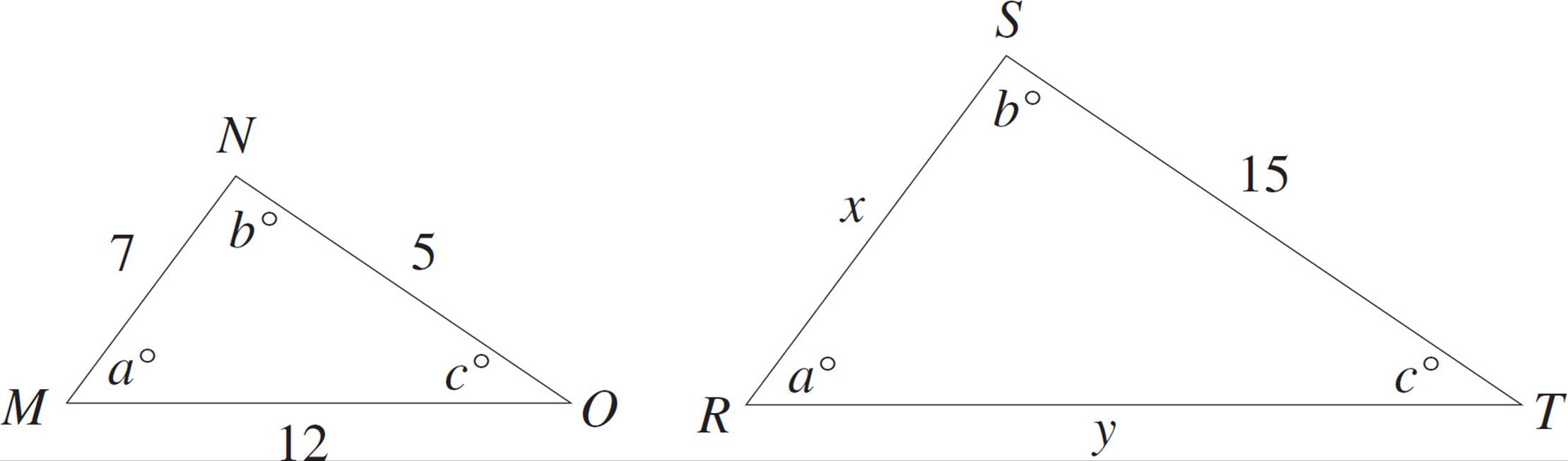
These two triangles both have the same set of angles, but they aren’t the same size. Whenever this is true, the sides of one triangle are proportional to those of the other. Notice that sides NO and ST are both opposite the angle that is a°. These are called corresponding sides, because they correspond to the same angle. So the lengths of NO and ST are proportional to each other. In order to figure out the lengths of the other sides we set up a proportion: 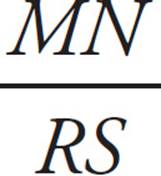 =
= 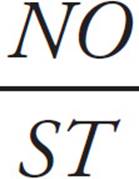 . Now fill in the information that you know:
. Now fill in the information that you know: ![]() =
= 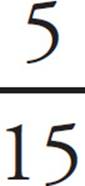 . Cross-multiply and you find that x = 21. You could also figure out the length of y:
. Cross-multiply and you find that x = 21. You could also figure out the length of y: 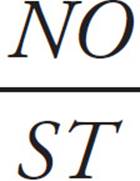 =
= 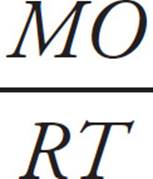 . So,
. So, 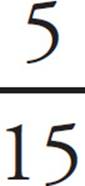 =
=  , and y = 36. Whenever you have to deal with sides of similar triangles, just set up a proportion.
, and y = 36. Whenever you have to deal with sides of similar triangles, just set up a proportion.
Finally, there’s a special relationship between similar triangles and trigonometry. Side lengths in similar triangles are proportional, and the trigonometric functions give the proportions of the sides of a triangle. Therefore, if two triangles are similar, the corresponding trigonometric functions are equal! Let’s look at how this might work in a problem.
![]()
16.
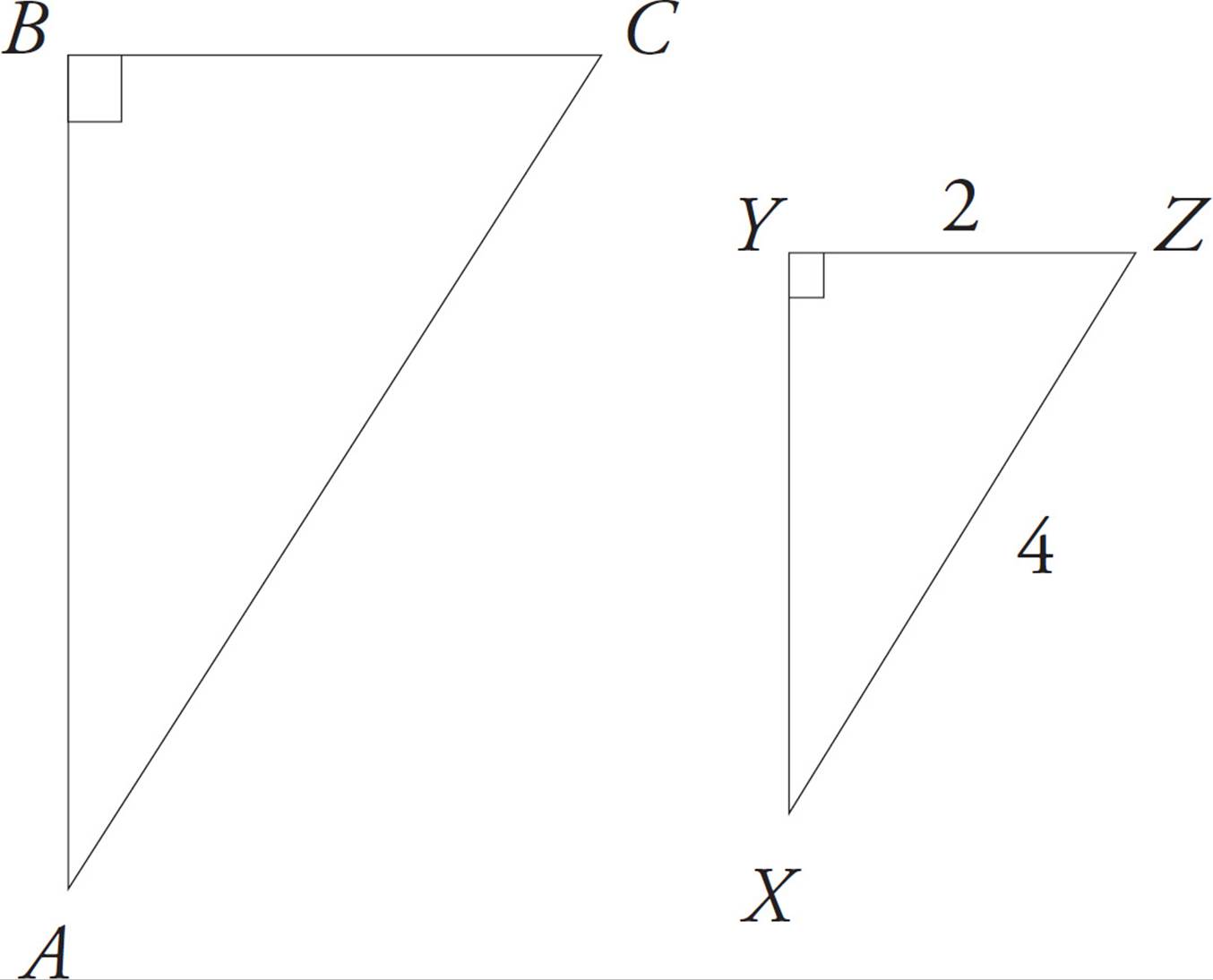
In the figure above, ΔABC is similar to ΔXYZ. What is the value of cos A?
A)![]()
B)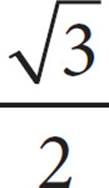
C)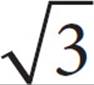
D)2
Here’s How to Crack It
Because the two triangles are similar, the value of corresponding trigonometric functions will be equal. Therefore, cos A = cos X. The value of cos X is 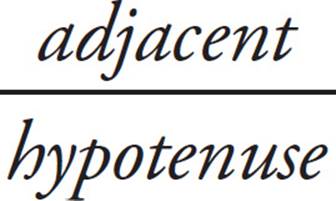 or
or 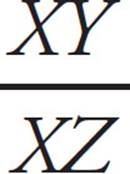 . You could use the Pythagorean theorem to find XY, but it’s easier to use the special right triangle discussed earlier. Because the hypotenuse is twice one of the legs, you know this is a 30°-60°-90° triangle. YZ is the shortest side (x), so XY is x
. You could use the Pythagorean theorem to find XY, but it’s easier to use the special right triangle discussed earlier. Because the hypotenuse is twice one of the legs, you know this is a 30°-60°-90° triangle. YZ is the shortest side (x), so XY is x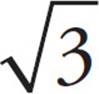 or 2
or 2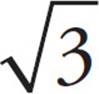 . Therefore, cos X =
. Therefore, cos X = 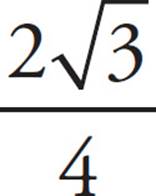 , which reduces to
, which reduces to 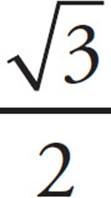 . Because cos X = cos A, cos A also equals
. Because cos X = cos A, cos A also equals 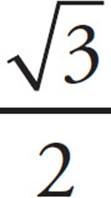 , which is (B).
, which is (B).
![]()
Circles
Here are the rules you’ll need to tackle circle questions on the SAT.
1.The circumference of a circle is 2πr or πd, where r is the radius of the circle and d is the diameter.
You’ll be given this information in your test booklet, so don’t stress over memorizing these formulas. You will always be able to refer to your test booklet if you forget them. Just keep in mind that the diameter is always twice the length of the radius (and that the radius is half the diameter).
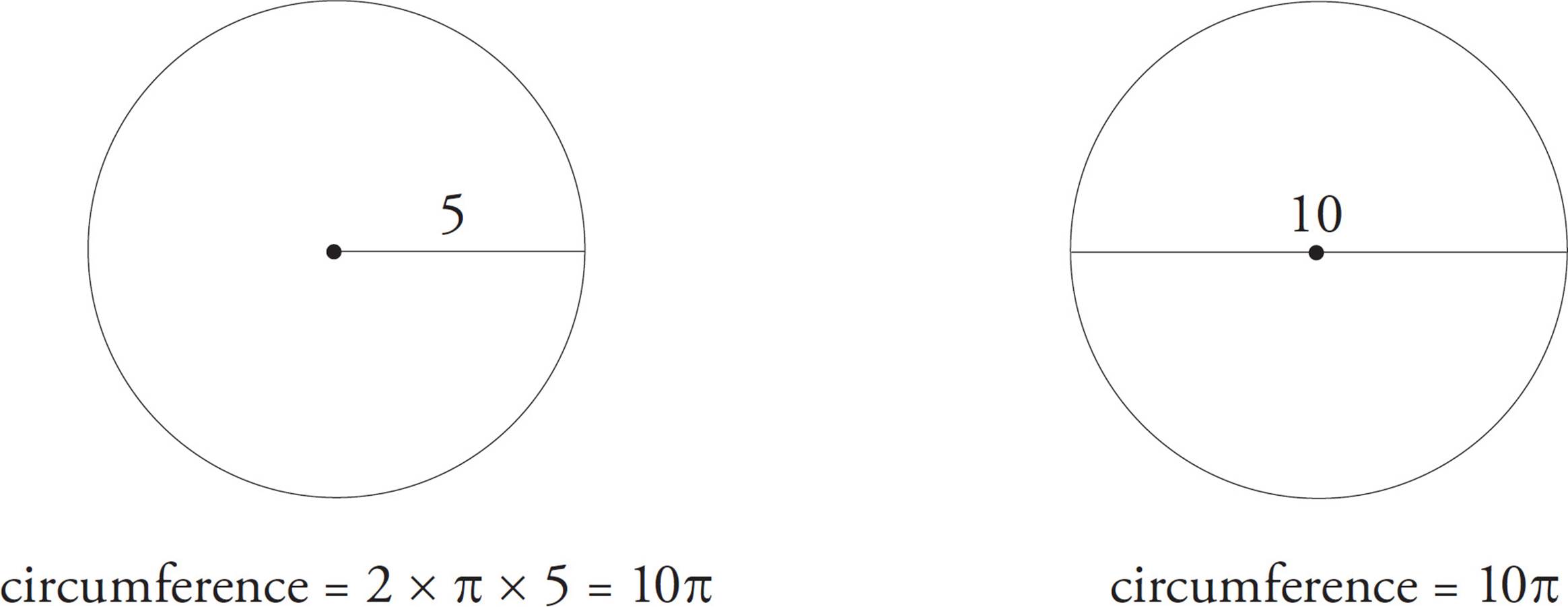
Some Formulas
Area = πr2
Circumference = 2πr or πd
Diameter = 2r
In math class you probably learned that π = 3.14 (or even 3.14159). On the SAT, π = 3+ (a little more than 3) is a good enough approximation. Even with a calculator, using π = 3 will give you all the information you need to solve difficult SAT multiple-choice geometry questions.
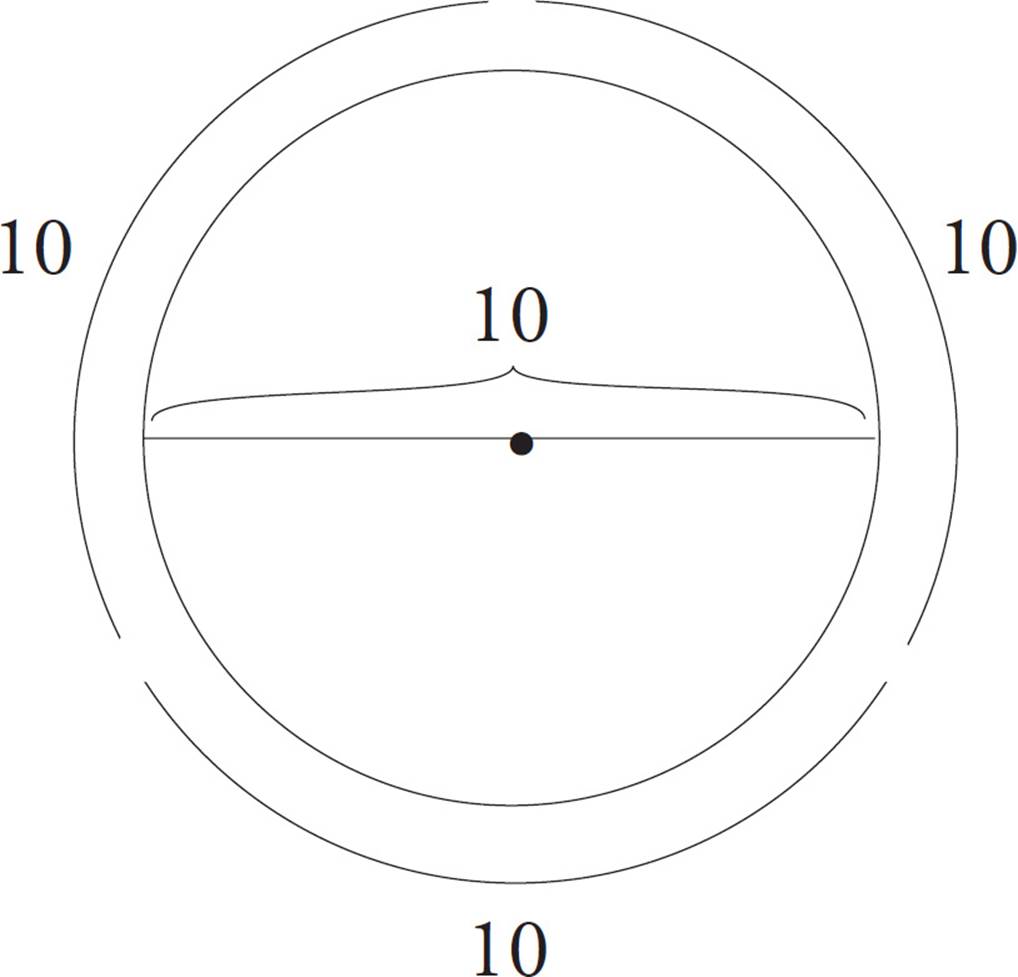
circumference = about 30
Leave That π Alone!
Most of the time, you
won’t multiply π out in
circle problems. Because
the SAT answers will
usually be in terms of π
(6π instead of 18.849…),
you can save yourself
some trouble by leaving
your work in terms of π.
2.The area of a circle is πr2, where r is the radius of the circle.
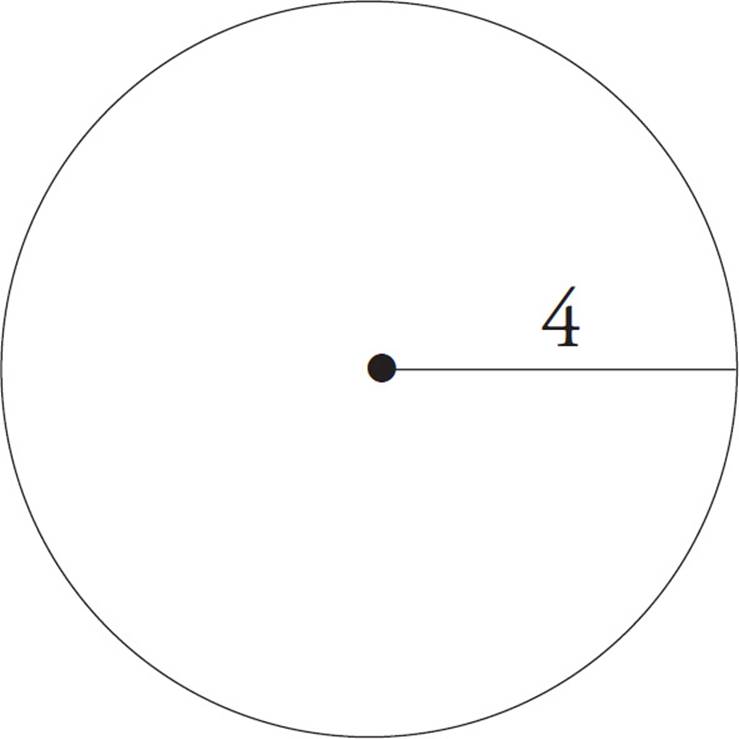
area = π42 = 16π
3.A tangent is a line that touches a circle at exactly one point. A radius drawn from that tangent point forms a 90-degree angle.
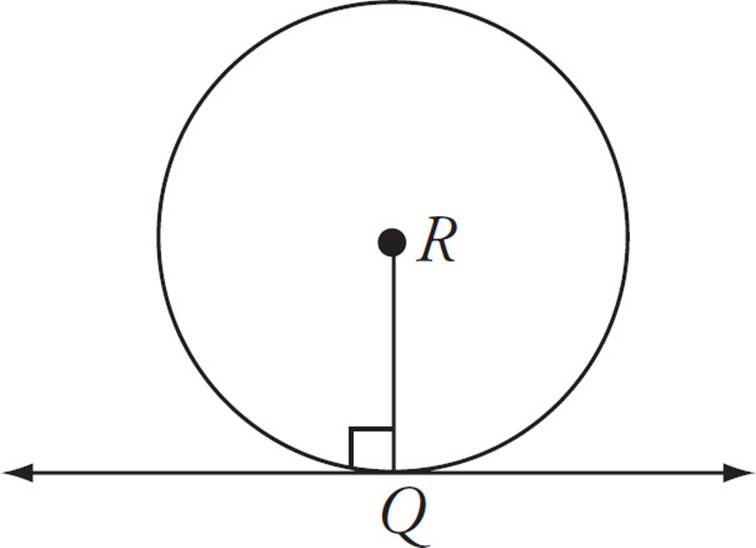
Circles Have Names?
If a question refers to
Circle R, it means that the
center of the circle
is point R.
Let’s see how these rules can show up on the SAT.
![]()

22.
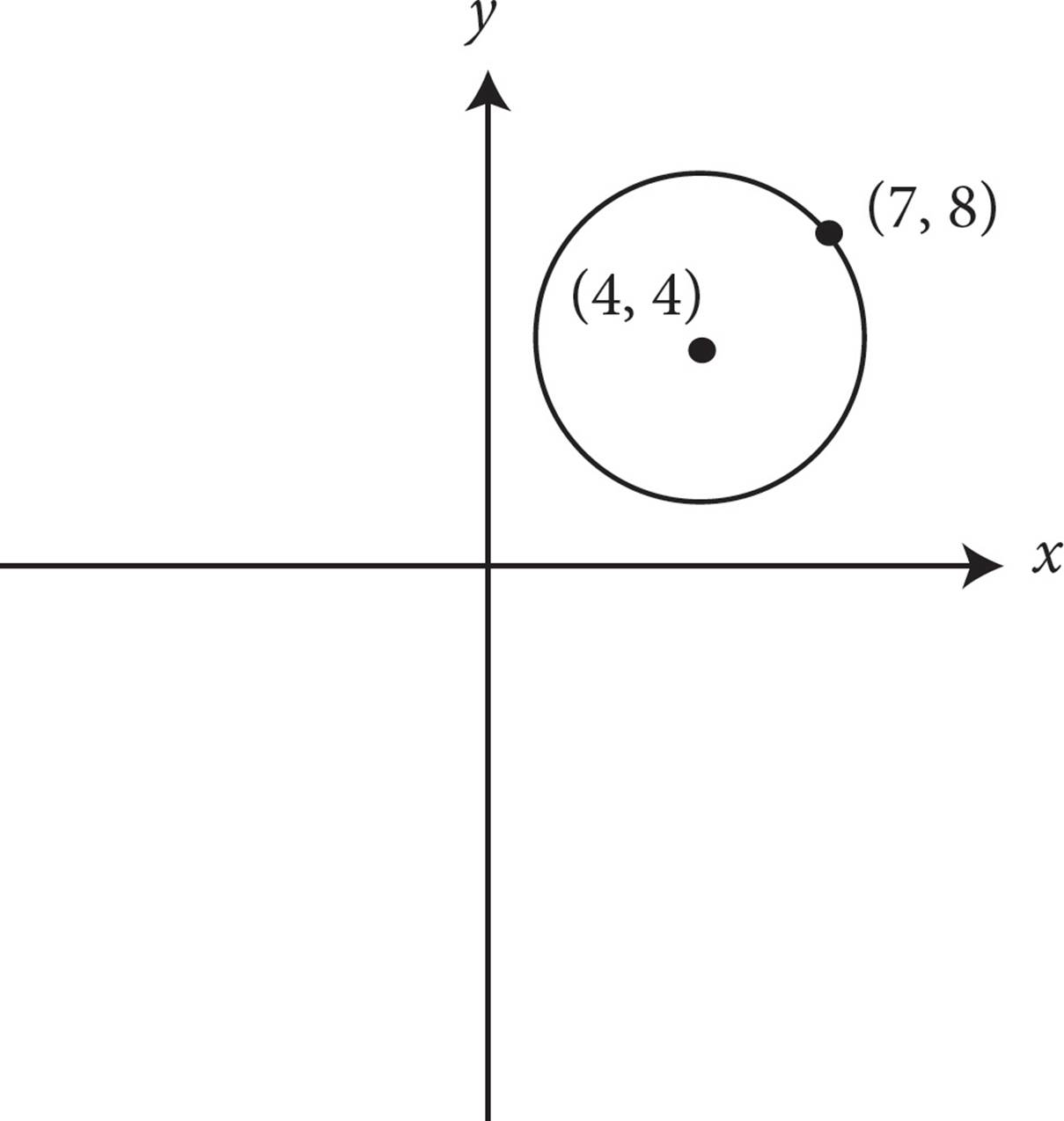
The circle defined by the equation (x − 4)2 + (y − 4)2 = 25 has its center at point (4, 4) and includes point (7, 8) on the circle. This is shown in the figure above. What is the area of the circle shown?
A)5π
B)10π
C)16π
D)25π
Here’s How to Crack It
You want the area, so write down the formula for area of a circle: A = π r2. That means you need to determine the radius of the circle. If you remember the circle formula from the previous chapter, you simply need to recall that r2 = 25 and just multiply by π to find the area. If not, you can find the distance between (4, 4) and (7, 8) by drawing a right triangle. The triangle is a 3-4-5 right triangle, so the distance between (4, 4) and (7, 8) (and thus the radius) is 5. If the radius is 5, then the area is π (5)2, or 25π. The answer is (D).
![]()
Arcs and Sectors
Many circle questions on the SAT will not ask about the whole circle. Rather, ETS will ask about arcs or sectors. Both arcs and sectors are portions of a circle: arcs are portions of the circumference, and sectors are portions of the area. Luckily, both arcs and sectors have the same relationship with the circle, based on the central angle (the angle at the center of the circle which creates the arc or sector):
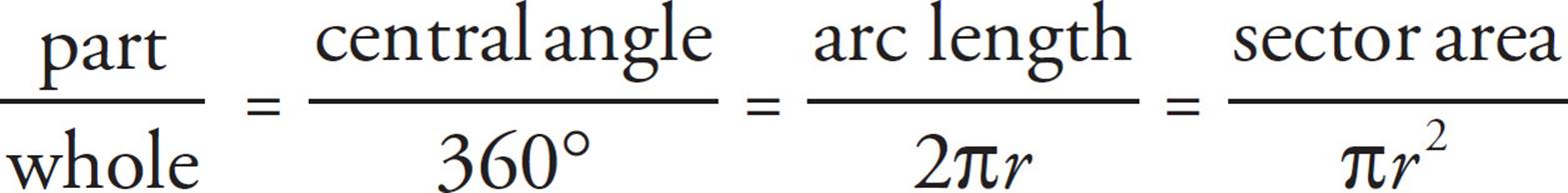
Note that these relationships are all proportions. Arcs and sectors are proportional to the circumference and area, respectively, as the central angle is to 360°.
Questions on the Math Test sometimes refer to “minor” or “major” arcs or sectors. A minor arc or sector is one that has a central angle of less than 180°, whereas a major arc or sector has a central angle greater than 180° (in other words, it goes the long way around the circle). Let’s see how arcs and sectors might show up in a problem.
![]()

15.Points A and B lie on circle O (not shown). AO = 3 and ∠AOB = 120°. What is the area of minor sector AOB?
A)![]()
B)π
C)3π
D)9π
Here’s How to Crack It
Because O is the name of the circle, it’s also the center of the circle, so AO is the radius. ∠AOB is the central angle of sector AOB, so you have all the pieces you need to find the sector. Put them into a proportion:
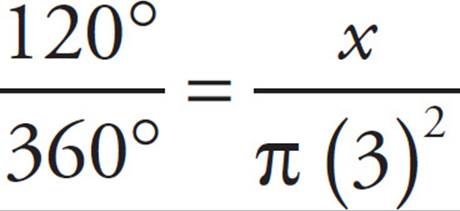
Cross-multiply to get 360x = 1,080π (remember to not multiply out π). Divide both sides by 360 and you get x = 3π, which is (C).
![]()
Relationship Between Arc and Angle in Radians
Sometimes ETS will ask for an arc length but will give you the angle in radians instead of degrees. Fear not! Rather than making the problem more complicated, the test writers have actually given you a gift! All you need to do is memorize this formula:
s = rθ
In this formula, s is the arc length, r is the radius, and θ is the central angle in radians. If you know this formula, these questions will be a snap!
Rectangles and Squares
Here are some rules you’ll need to know about rectangles and squares:
1.The perimeter of a rectangle is the sum of the lengths of its sides.
Just add them up.
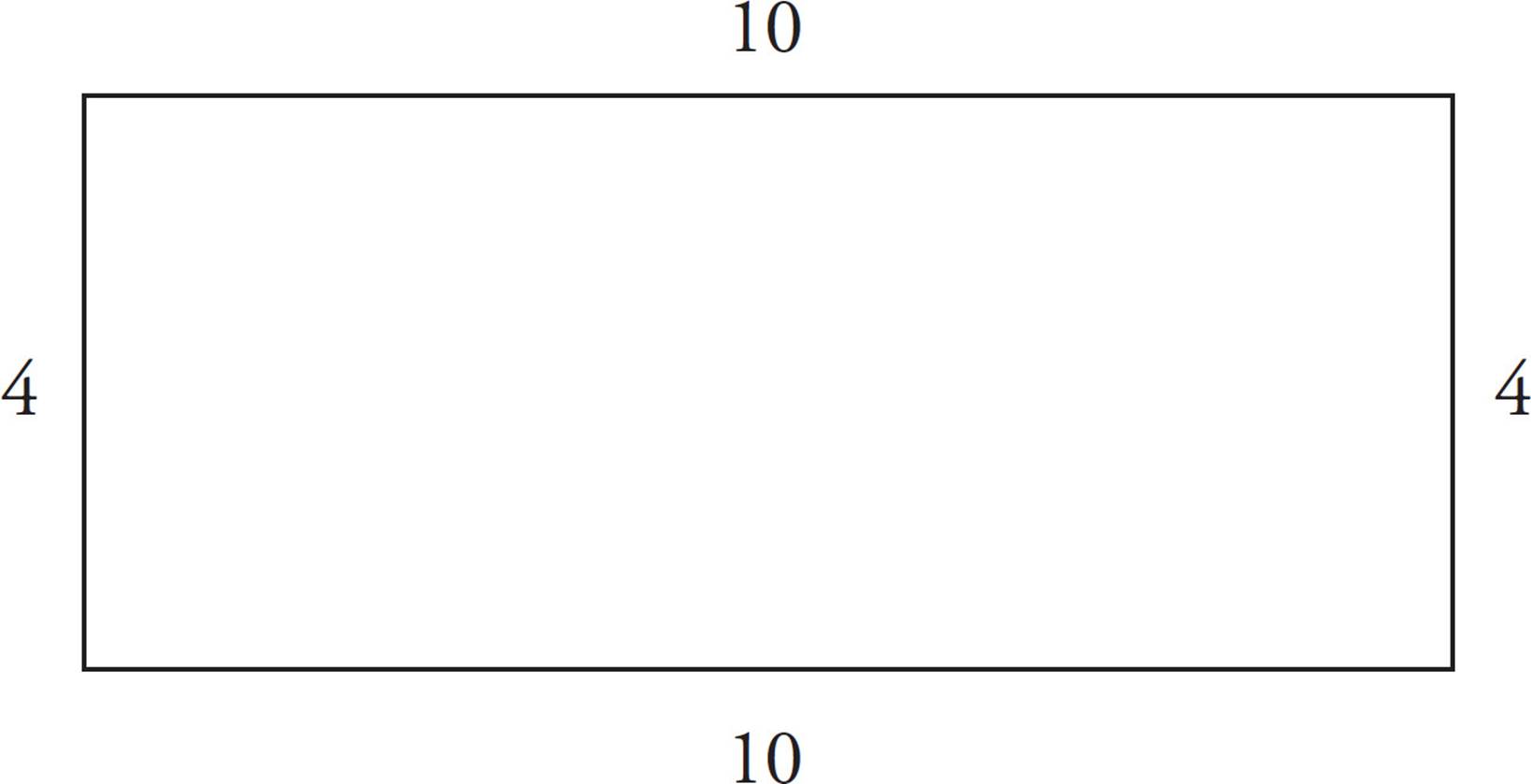
perimeter = 10 + 4 + 10 + 4 = 28
2.The area of a rectangle is length × width.
The area of the preceding rectangle, therefore, is 10 × 4, or 40.
3.A square is a rectangle whose four sides are all equal in length.
The perimeter of a square, therefore, is four times the length of any side. The area is the length of any side squared.
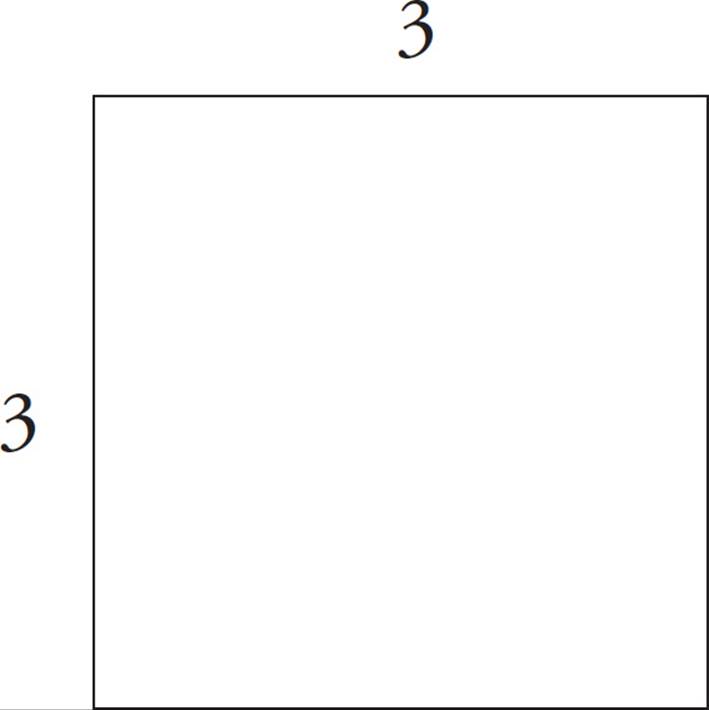
perimeter = 4 (3) = 12
area = 32 = 9
4.In rectangles and squares all angles are 90-degree angles.
It can’t be a square or a rectangle unless all angles are 90 degrees.
Little Boxes
Here’s a progression of
quadrilaterals from least
specific to most specific:
quadrilateral is any
4-sided figure
↓
parallelogram is
a quadrilateral in which
opposite sides are parallel
↓
rectangle is
a parallelogram in which
all angles = 90 degrees
↓
square is a rectangle in
which all sides are equal
Let’s check out an example.
![]()

6.If the perimeter of a square is 28, what is the length of the diagonal of the square?
A)2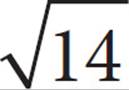
B)7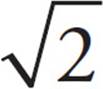
C)7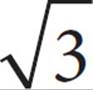
D)14
Here’s How to Crack It
The perimeter of a square is 4s. So, 28 = 4s. Divide by 4 to find s = 7. The diagonal of a square divides the square into two 45°-45°-90° triangles, with sides in the ratio of x:x:x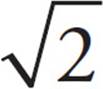 . If the side is 7, the diagonal is 7
. If the side is 7, the diagonal is 7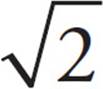 . The answer is (B).
. The answer is (B).
![]()
Polygons
Polygons are two-dimensional figures with three or more straight sides. Triangles and rectangles are both polygons. So are figures with five, six, seven, eight, or any greater number of sides. The most important fact to know about polygons is that any one of them can be divided into triangles. This means that you can always determine the sum of the measures of the interior angles of any polygon.
For example, the sum of the interior angles of any four-sided polygon (called a quadrilateral) is 360 degrees. Why? Because any quadrilateral can be divided into two triangles, and a triangle contains 180 degrees. Look at the following example:
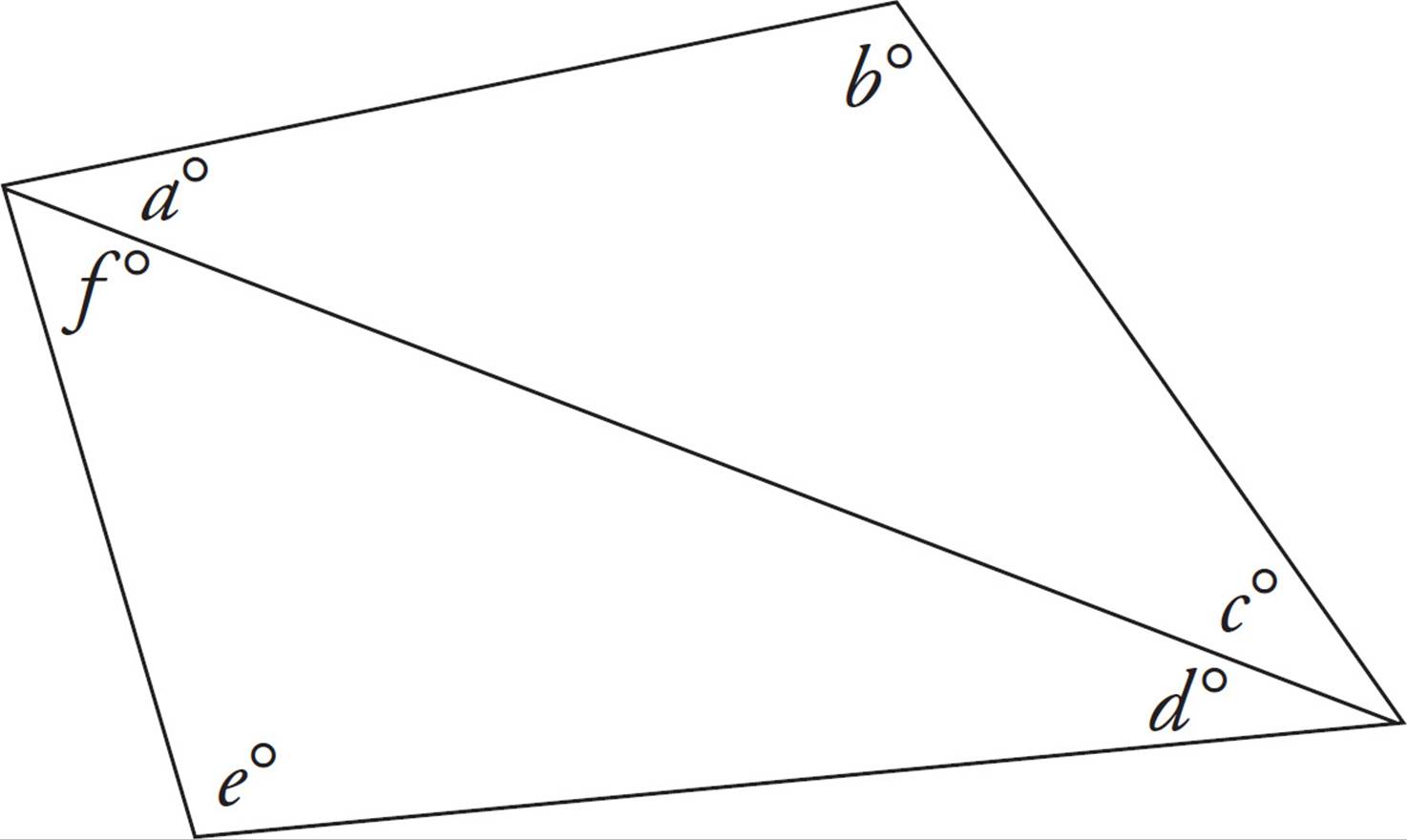
In this polygon, a + b + c = 180 degrees; so does d + e + f. That means that the sum of the interior angles of the quadrilateral must be 360 degrees (a + b + c + d + e + f).
A parallelogram is a quadrilateral whose opposite sides are parallel. In the following parallelogram, side AB is parallel to side DC, and AD is parallel to BC. Because a parallelogram is made of two sets of parallel lines that intersect each other, we know that the two big angles are equal, the two small angles are equal, and a big angle plus a small angle equals 180 degrees. In the figure below, big angles A and C are equal, and small angles B and D are equal. Also, because A is a big angle and D is a small angle, A + D = 180 degrees.

Need the Formula?
You may have learned the
formula for this in math
class. If so, you can use
it: The sum of the degrees
in an n-sided polygon is
180(n − 2). If you don’t
know the formula, don’t
worry about memorizing it.
It doesn’t come up much,
and when it does come up,
you can always break up
the polygon into triangles.
Let’s try an example:
![]()
12.
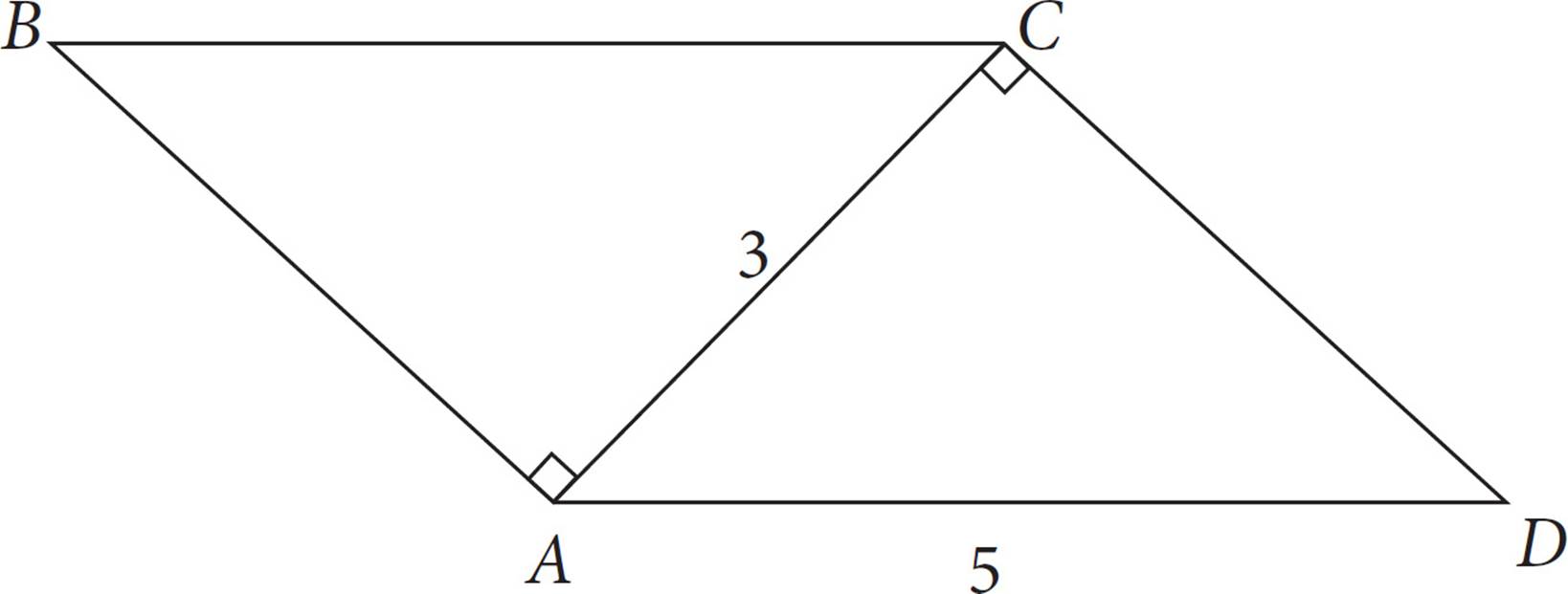
Note: Figure not drawn to scale.
In parallelogram ABCD above, AC = 3 and AD = 5. What is the area of ABCD ?
A)12
B)15
C)18
D)20
Here’s How to Crack It
The trick is to notice that this parallelogram is actually made of two equal triangles. By finding the area of the triangles, you can find the area of the parallelogram. The triangles are both right triangles, and the two sides given in the figure follow the 3-4-5 pattern. If you look at triangle ACD with AC as the base, the base is 3 and the height is 4. Now use the formula for area of a triangle:
A = ![]() × 3 × 4 = 6
× 3 × 4 = 6
That means the parallelogram is 2 × 6 = 12.
Also, if you estimate the area, the base is 5 and the height is less than 3, so the area is less than 15. The only answer less than 15 is (A).
![]()
Volume
Volume questions on the SAT can seem intimidating at times. ETS loves to give you questions featuring unusual shapes such as pyramids and spheres. Luckily, at the beginning of the Math sections (and the beginning of this chapter), you’re given a box with all the formulas you will ever need for volume questions on the SAT. Simply apply the Basic Approach using the given formulas and you’ll be in good shape (pun entirely intended)!
Let’s look at an example:
![]()
15.A sphere has a volume of 36π. What is the surface area of the sphere? (The surface area of a sphere is given by the formula A = 4πr2.)
A)3π
B)9π
C)27π
D)36π
Here’s How to Crack It
Start by writing down the formula for volume of a sphere from the beginning of the chapter: V = ![]() πr3. Put what you know into the equation: 36π =
πr3. Put what you know into the equation: 36π = ![]() πr3. From this you can solve for r. Divide both sides by π to get 36 =
πr3. From this you can solve for r. Divide both sides by π to get 36 = ![]() r3. Multiply both sides by 3 to clear the fraction: 36(3) = 4r3. Note we left 36 as 36, because the next step is to divide both sides by 4, and 36 divided by 4 is 9, so 9(3) = r3 or 27 = r3. Take the cube root of both sides to get r = 3. Now that you have the radius, use the formula provided to find the surface area: A = 4π(3)2, which comes out to 36π, which is (D).
r3. Multiply both sides by 3 to clear the fraction: 36(3) = 4r3. Note we left 36 as 36, because the next step is to divide both sides by 4, and 36 divided by 4 is 9, so 9(3) = r3 or 27 = r3. Take the cube root of both sides to get r = 3. Now that you have the radius, use the formula provided to find the surface area: A = 4π(3)2, which comes out to 36π, which is (D).
![]()
Ballparking
You may be thinking, “Wait a second, isn’t there an easier way?” By now, you should know that of course there is, and we’re going to show you. On many SAT geometry problems, you won’t have to calculate an exact answer. Instead, you can estimate an answer choice. We call this Ballparking, a strategy we discussed earlier in this book.
Ballparking is extremely useful on SAT geometry problems. At the very least, it will help you avoid careless mistakes by immediately eliminating answers that could not possibly be correct. In many problems, Ballparking will allow you to find ETS’s answer without even working out the problem at all.
Pictures
Unless otherwise stated,
any diagram ETS supplies
you with is drawn to scale.
For example, on many SAT geometry problems, you will be presented with a drawing in which some information is given and you will be asked to find some of the information that is missing. In most such problems, ETS expects you to apply some formula or perform some calculation, often an algebraic one. But you’ll almost always be better off if you look at the drawing and make a rough estimate of ETS’s answer (based on the given information) before you try to work it out.
Rocket Science?
The SAT is a goofy college
admissions test, not an
exercise in precision.
Because 45 of its 58 Math
questions are multiple-choice,
you can afford to
approximate numbers like
π,  , and
, and  (3+, 1.4, and
(3+, 1.4, and
1.7+, respectively).
The basic principles you just learned (such as the number of degrees in a triangle and the fact that π ≈ 3) will be enormously helpful to you in Ballparking on the SAT. You should also know the approximate values of several common square roots. Be sure to memorize them before moving on. Knowing them cold will help you solve problems and save time, especially when calculator use is not allowed.
Square Roots
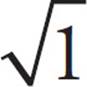 = 1
= 1
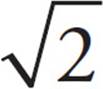 ≈ 1.4
≈ 1.4
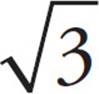 ≈ 1.7+
≈ 1.7+
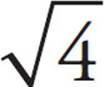 = 2
= 2
Happy Holidays!
February 14 (2/14) is
Valentine’s Day, so = 1.4.
= 1.4.
March 17 (3/17) is
St. Patrick’s Day, so = 1.7.
= 1.7.
You will also find it very helpful if you have a good sense of how large certain common angles are. Study the following examples.
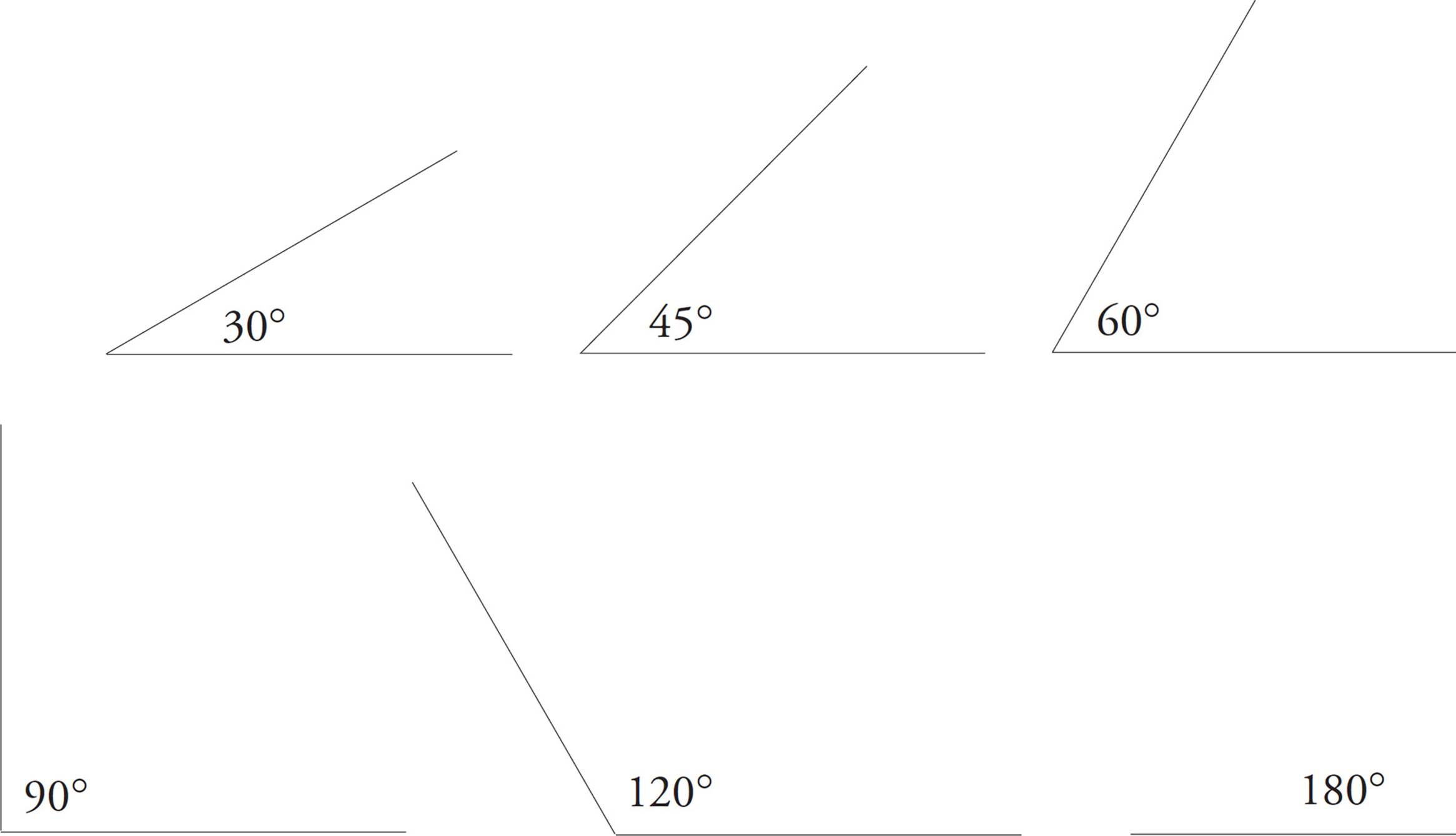
How High Is the Ceiling?
If your friend stood next to a wall in your living room and asked you how high the ceiling was, what would you do? Would you get out your trigonometry textbook and try to triangulate using the shadow cast by your pal? Of course not. You’d look at your friend and think something like this: “Dave’s about 6 feet tall. The ceiling’s a couple of feet higher than he is. It must be about 8 feet high.”
Your ballpark answer wouldn’t be exact, but it would be close. If someone later claimed that the ceiling in the living room was 15 feet high, you’d be able to tell her with confidence that she was mistaken.
You’ll be able to do the same thing on the SAT. Every geometry figure on your test will be drawn exactly to scale unless there is a note in that problem telling you otherwise. That means you can trust the proportions in the drawing. If line segment A has a length of 2 and line segment B is exactly half as long, then the length of line segment B is 1. All such problems are ideal for Ballparking.
The Correct Choice
Remember that the SAT
is a multiple-choice
test. This means that
you don’t always have to
come up with an answer;
you just have to
identify the correct one
from among the four
choices provided.
Plugging In
As you learned already, Plugging In is a powerful technique for solving SAT algebra problems. It is also very useful on geometry problems. On some problems, you will be able to plug in ballpark values for missing information and then use the results either to find the answer directly or to eliminate answers that could not possibly be correct.
Here’s an example:
![]()

20.The base of triangle T is 40 percent less than the length of rectangle R. The height of triangle T is 50 percent greater than the width of rectangle R. The area of triangle T is what percent of the area of rectangle R ?
A)10
B)45
C)90
D)110
Here’s How to Crack It
This is a really hard problem. Don’t worry—you’ll still be able to find the right answer by sketching and plugging in.
When plugging in, always use numbers that are easy to work with. Let’s say the length of the rectangle is 10; that means that the base of the triangle, which is 40 percent smaller, is 6. Now if we plug 4 in for the width of rectangle R, then the height of triangle T is 6. You should come up with two sketches that look like this:
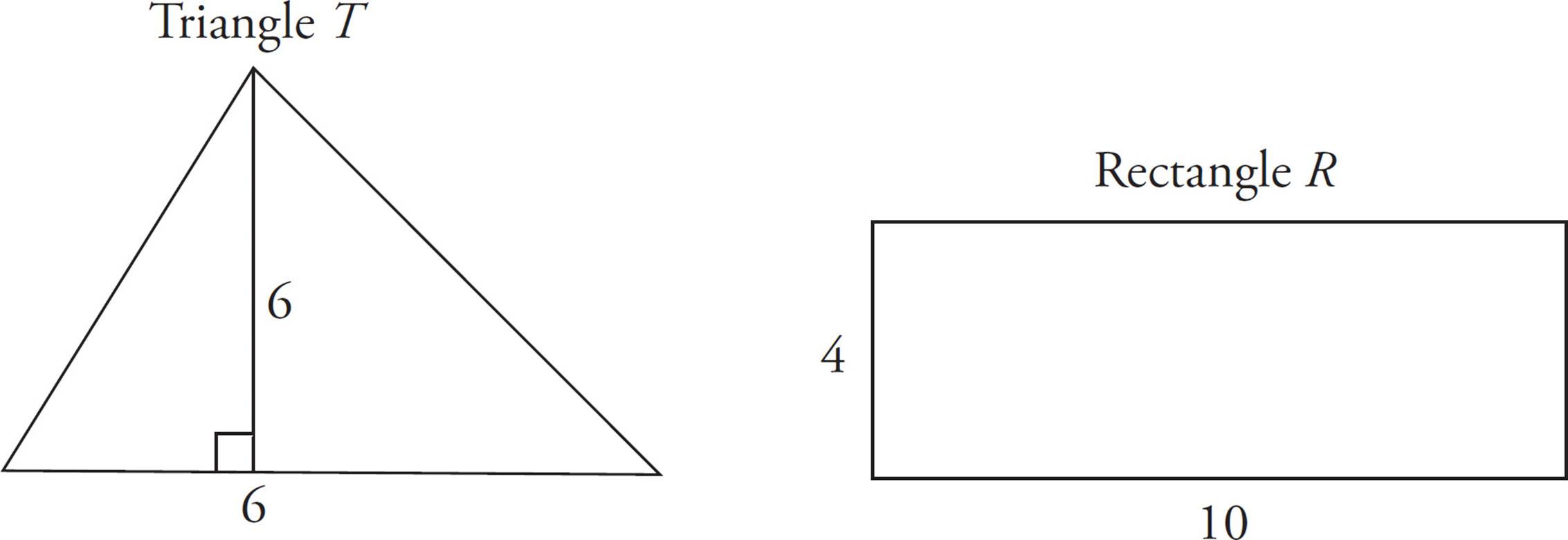
T has an area of ![]() bh, or 18. R has an area of 40. Now set up the translation: 18 =
bh, or 18. R has an area of 40. Now set up the translation: 18 = 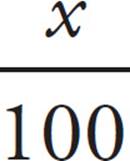 (40), where x represents what percent the triangle is of the rectangle.
(40), where x represents what percent the triangle is of the rectangle.
Solve for x and you get 45. The correct answer is (B).
![]()
Geometry Drill 1: No Calculator Section
Work these Geometry questions with all your skills and knowledge, but without your calculator. Answers and explanations can be found on this page.
2.
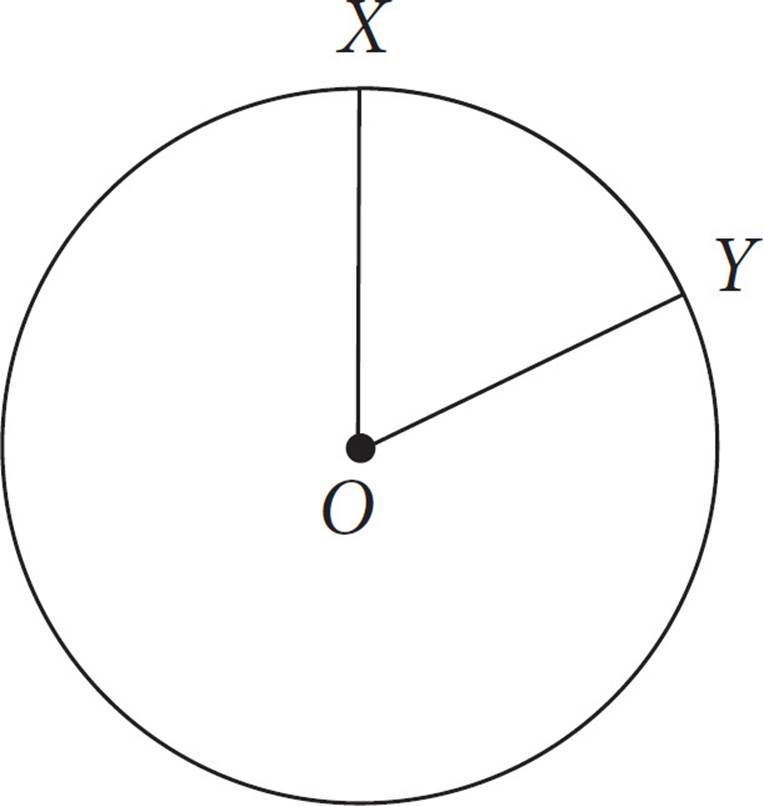
In the figure above, circle O has a radius of 8, and angle XOY measures 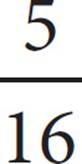 π radians. What is the measure of minor arc XY ?
π radians. What is the measure of minor arc XY ?
A)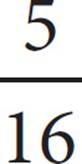 π
π
B)![]() π
π
C)5π
D)16π
3.
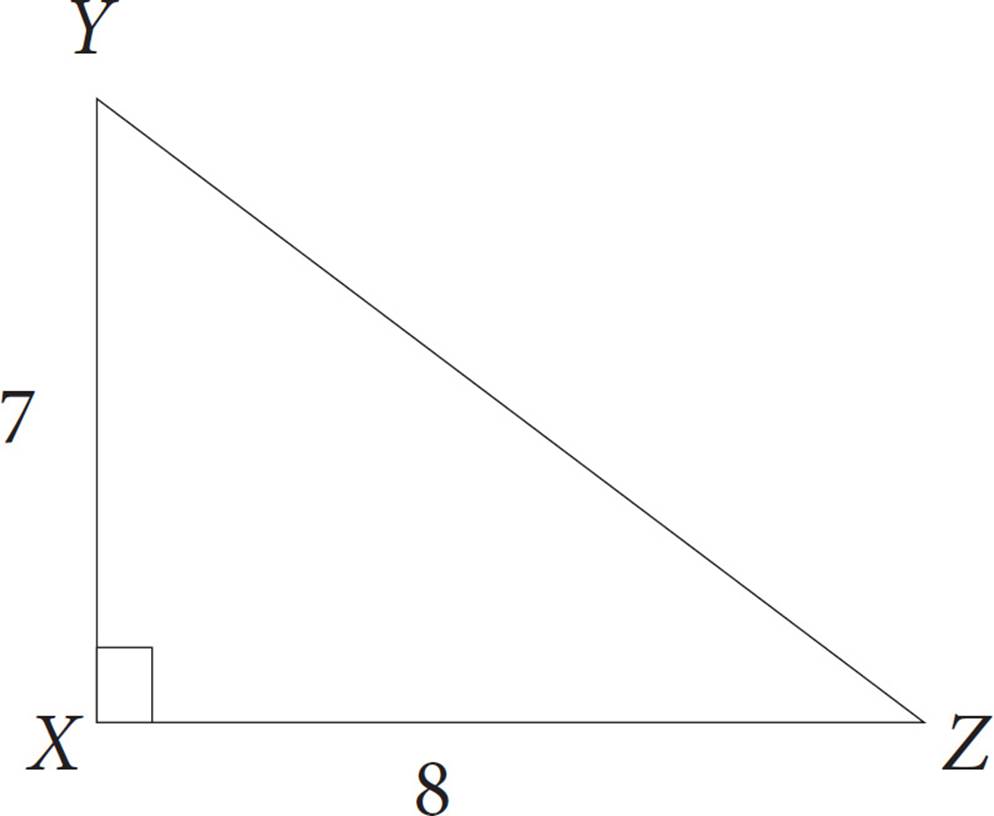
What is the value of tan ∠XZY ?
A)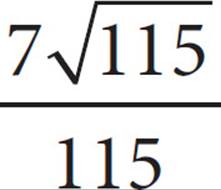
B)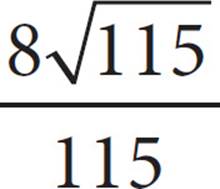
C)![]()
D)![]()
10.
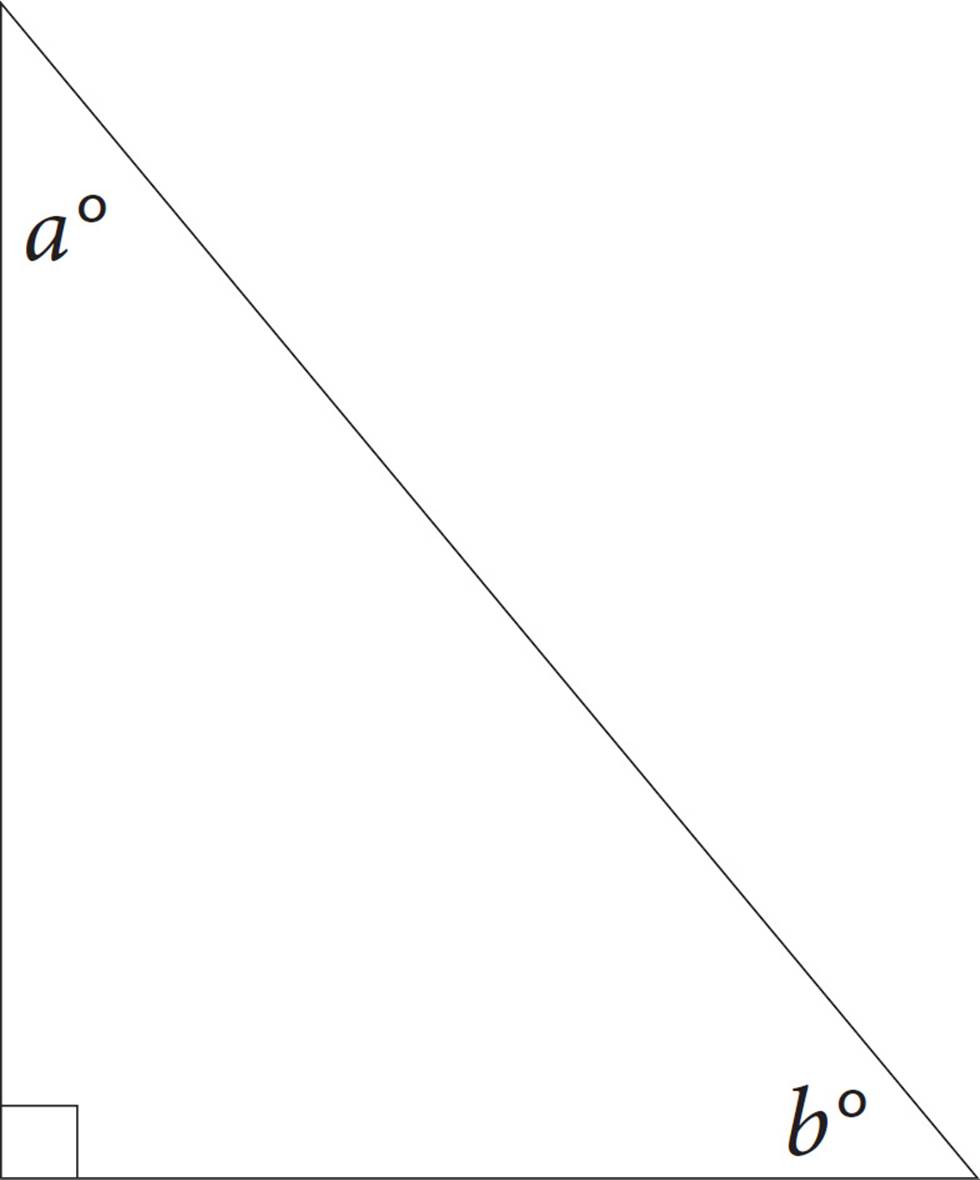
In the figure above, sin a = x. What is the value of cos b?
A)x
B)
C)|1 − x|
D)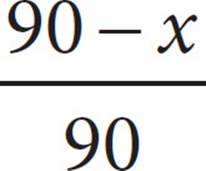
15.
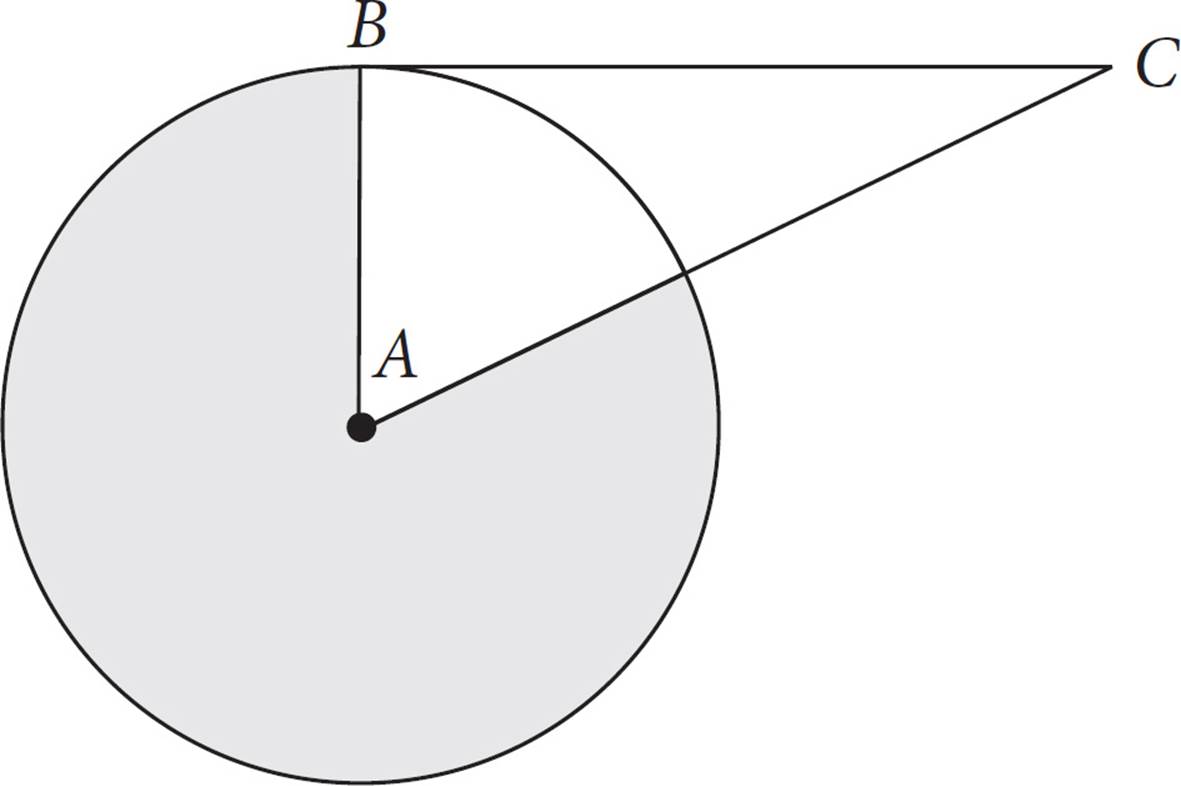
Note: Figure not drawn to scale.
The circle above with center A has an area of 21. BC is tangent to the circle with center A at point B. If AC = 2AB, then what is the area of the shaded region?
A)3.5
B)15.75
C)17.5
D)21
Geometry Drill 2: Calculator-Permitted Section
Calculator use is allowed on these questions, so use it to your best ability, but make sure to set them up on paper first. Answers and explanations can be found on this page.
1.If a rectangular swimming pool has a volume of 16,500 cubic feet, a uniform depth of 10 feet, and a length of 75 feet, what is the width of the pool, in feet?
A)22
B)26
C)32
D)110
8.
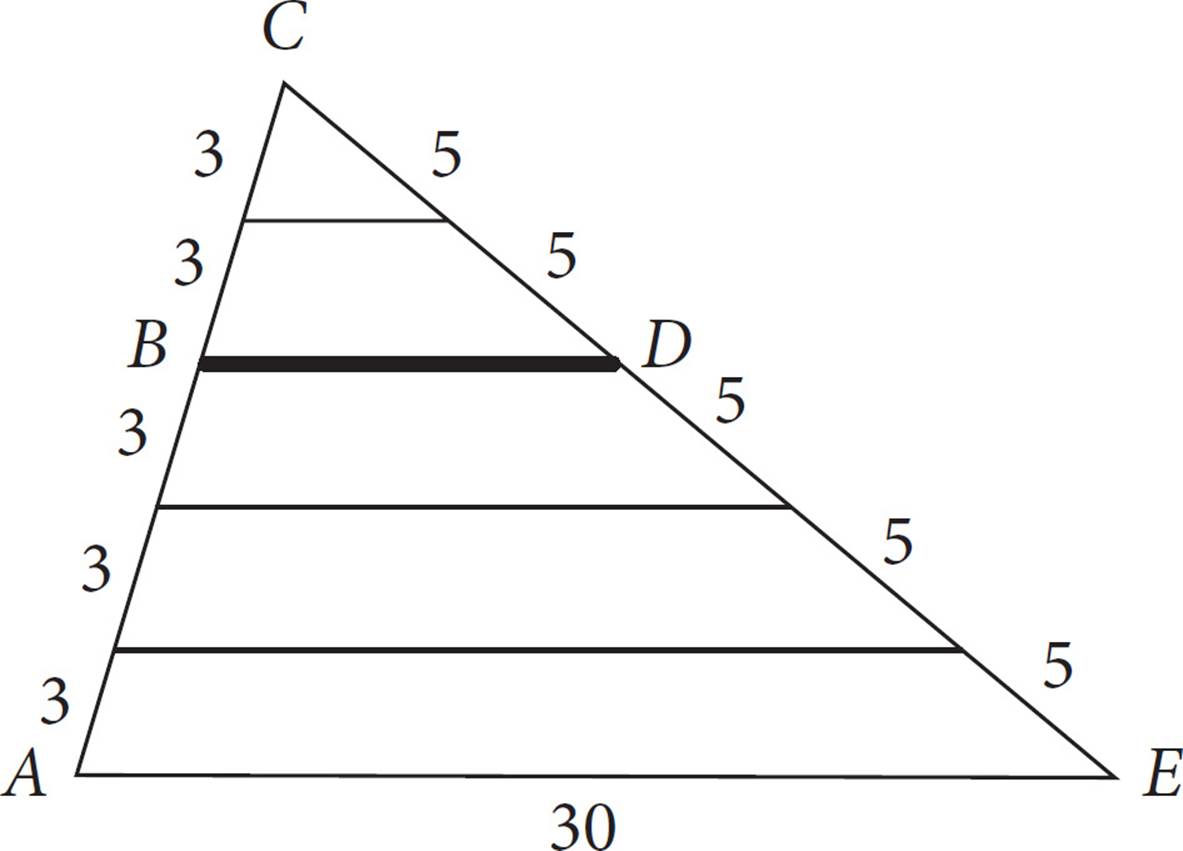
In the figure above, what is the length of 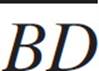 ?
?
A) 8
B) 9
C) 12
D) 15
12.
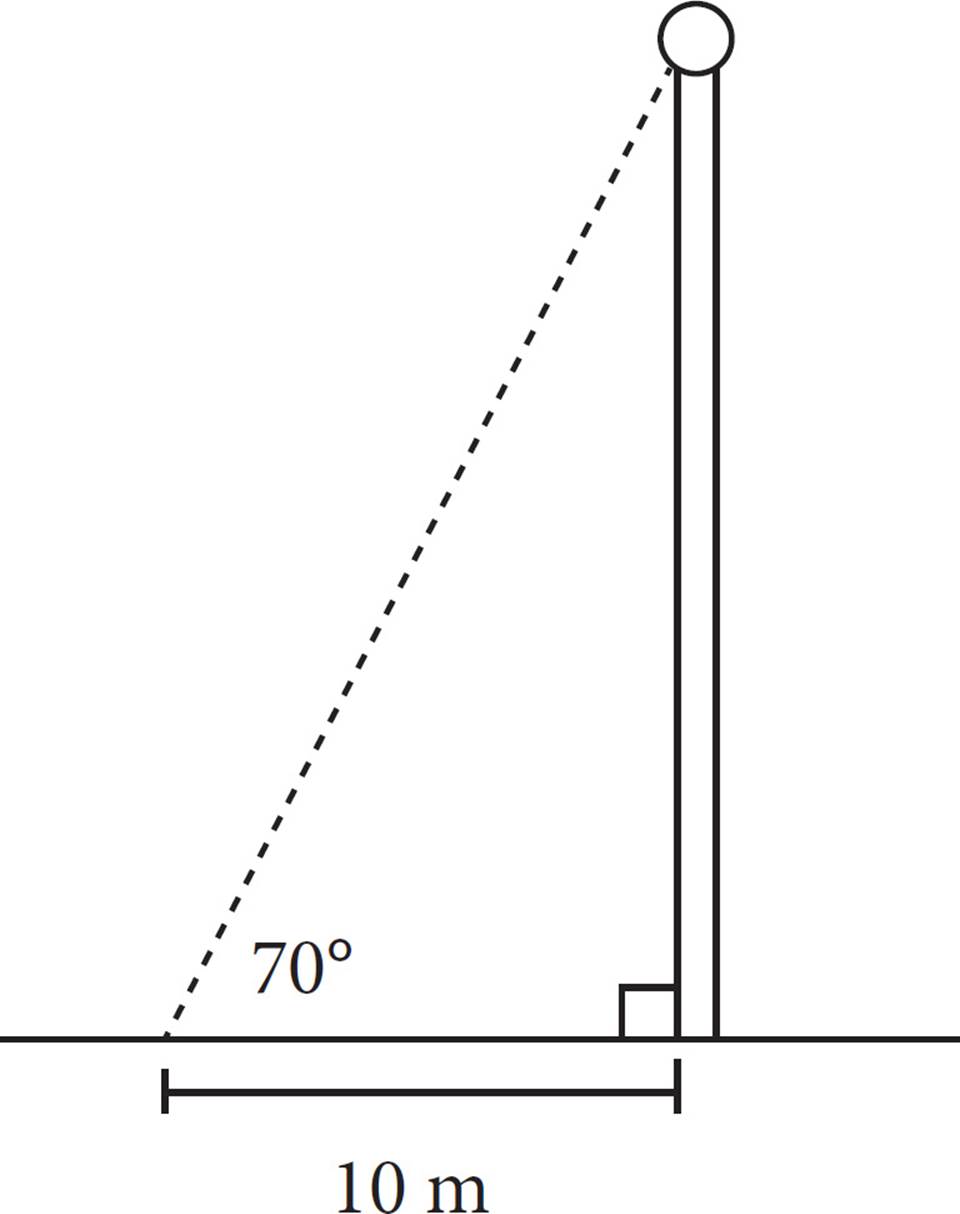
Martin wants to know how tall a certain flagpole is. Martin walks 10 meters from the flagpole, lies on the ground, and measures an angle of 70° from the ground to the base of the ball at the top of the flagpole. Approximately how tall is the flagpole from the ground to the base of the ball at the top of the flagpole?
A)3 m
B)9 m
C)27 m
D)29 m
26.
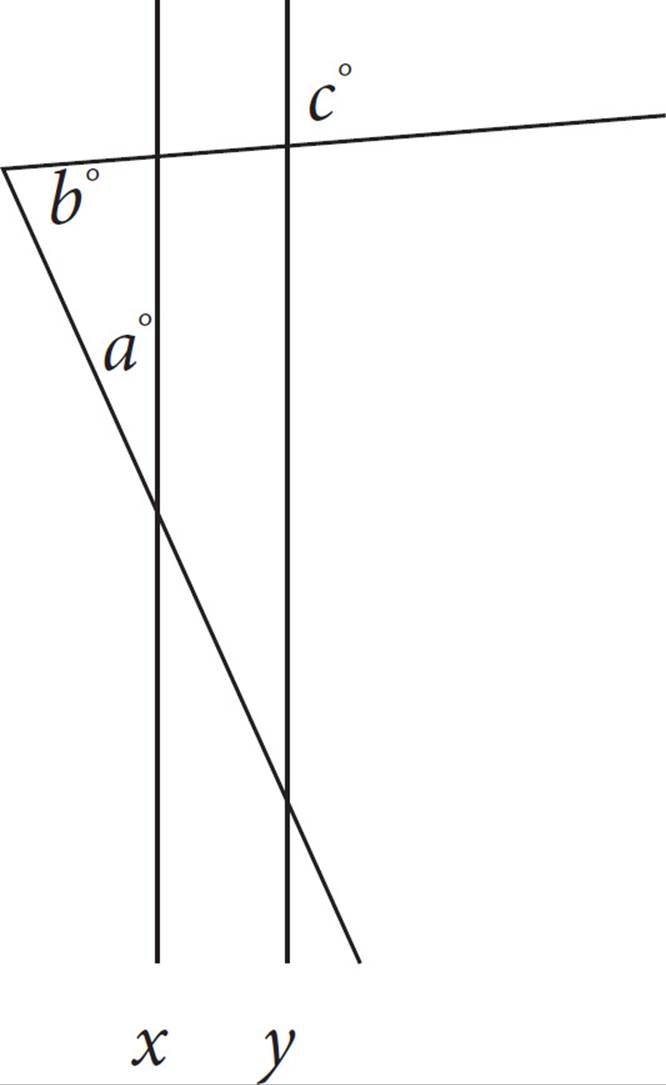
In the figure above, x || y. What is the value of a ?
A)b + c
B)2b − c
C)180 − b + c
D)180 − b − c
28.
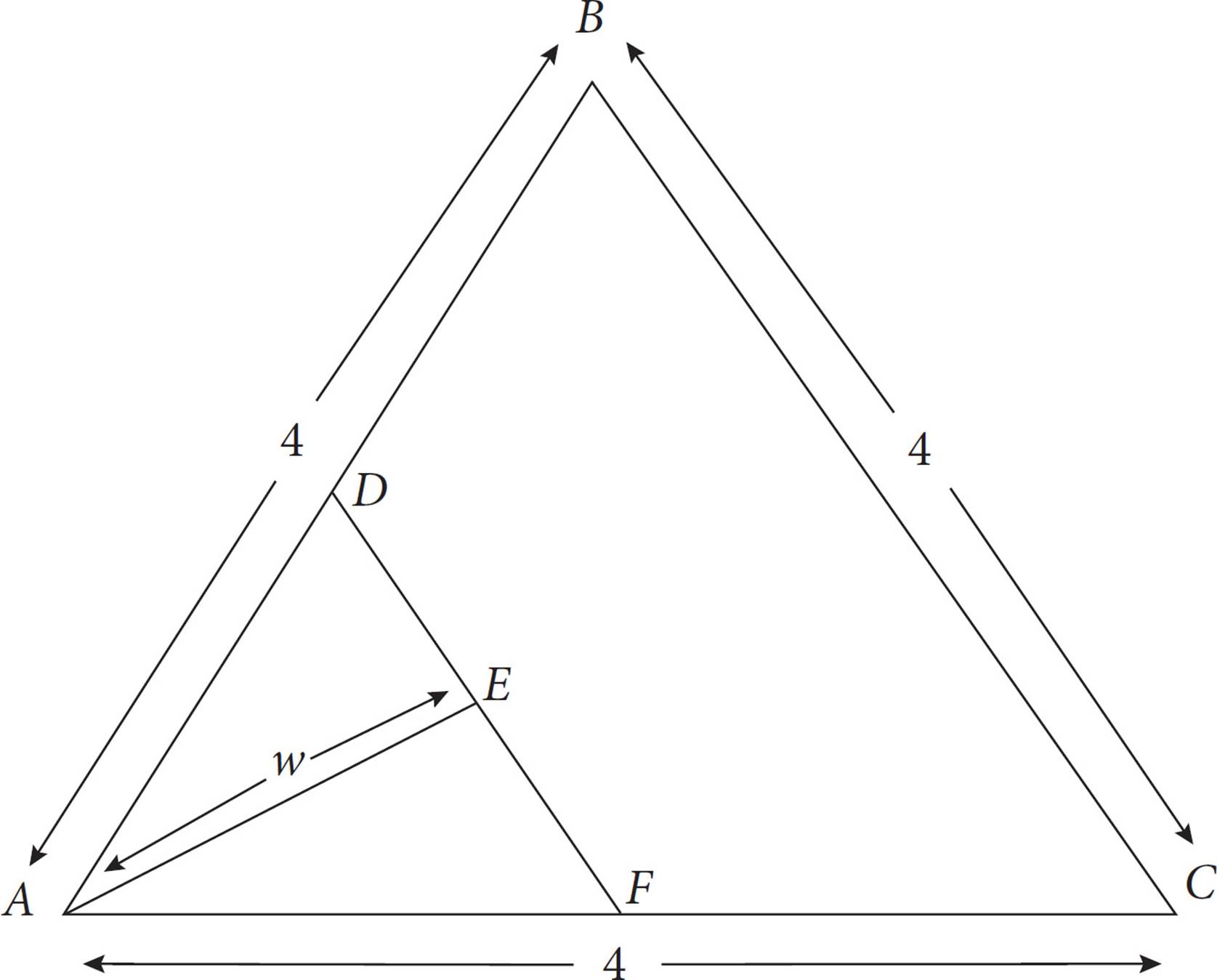
ΔABC is equilateral and ∠AEF is a right angle. D and F are the midpoints of AB and AC, respectively. What is the value of w ?
A)1
B)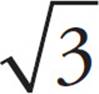
C)2
D)2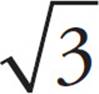
29.A toy pyramid (not shown) is made from poly(methyl methacrylate), better known by its trade term Lucite. The toy pyramid has a regular hexagonal base of 15 cm2 and a height of 4 cm. In the base of the pyramid, there is a semispherical indentation 2 cm in diameter. If the pyramid weighs 21.129 g, then what is the density of Lucite? (Density equals mass divided by volume.)
A)1.06 g/cm3
B)1.18 g/cm3
C)2.09 g/cm3
D)6.51 g/cm3
CHAPTER DRILL ANSWERS AND EXPLANATIONS
Geometry Drill 1: No Calculator Section
2. BBecause the question wants arc length and gives you the measure of the central angle in radians, you can use the formula s = rθ to find the arc length: s = (8)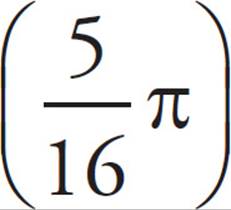 =
= 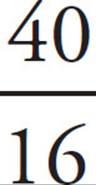 π, which reduces to
π, which reduces to ![]() π, which is (B).
π, which is (B).
3. CTangent is defined as 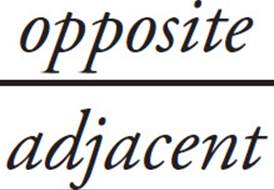 . The side opposite angle XZY is 7, and the side adjacent to this angle is 8, so the tangent of ∠XYZ =
. The side opposite angle XZY is 7, and the side adjacent to this angle is 8, so the tangent of ∠XYZ = ![]() , which is (C).
, which is (C).
10. AYou can plug in when you’re dealing with a geometry problem with unknowns. When you’re Plugging In for a right triangle, use one of the special right triangles to make your life easier. Use a 3-4-5 right triangle. Make the side opposite a 3, the side adjacent to a 4, and the hypotenuse 5. Because sine is 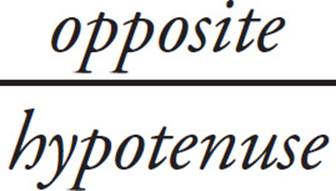 , sin a =
, sin a = ![]() , so x =
, so x = ![]() . Cosine is
. Cosine is 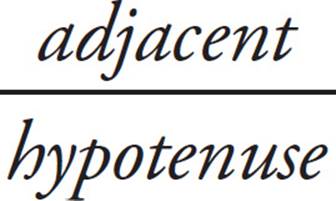 , so cosb =
, so cosb = ![]() . This is your target; circle it. Make x =
. This is your target; circle it. Make x = ![]() in each answer choice and look for the answer which equals
in each answer choice and look for the answer which equals ![]() . Only (A) works.
. Only (A) works.
15. CThe trick is to recognize that DABC is a 30°-60°-90° right triangle. ∠ABC must equal 90° since a tangent line must be perpendicular to the radius of a circle drawn to the point of tangency. Only a 30°-60°-90° has a hypotenuse (AC) equal to double the length of one of the sides (AB). (You can also use the Pythagorean theorem to show this.) This means that ∠BAC = 60°, so the shaded region has a central angle measure of 360° − 60° = 300°. To get the area, use the proportion 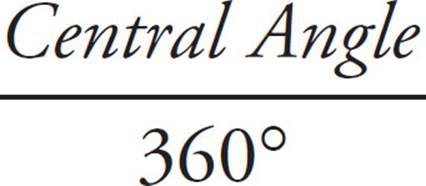 =
= 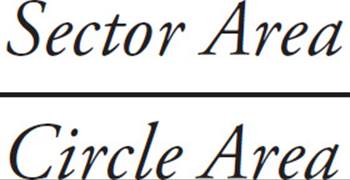 , or
, or 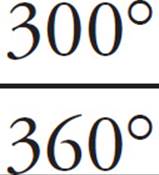 =
= 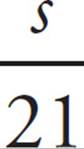 . Reduce, cross-multiply, and solve to get s = 17.5. This matches (C).
. Reduce, cross-multiply, and solve to get s = 17.5. This matches (C).
Geometry Drill 2: Calculator-Permitted Section
1. AFor this question, you need to know that volume equals length × width × height. You know that the volume is 16,500, the depth (or height) is 10, and the length is 75. Just put those numbers in the formula: 16,500 = 75 × w × 10. Use your calculator to solve for w, which equals 22: (A).
8. CThe 5 equal lengths that make up the two sides of the largest triangle tell us that we are dealing with 5 similar triangles. The largest triangle has sides 15:25:30, and the sides of all 5 triangles will have an equivalent ratio. Reduced, the ratio is 3:5:6, which happens to be the dimensions of the smallest triangle. We want to find the length of BD, the base of a triangle with sides of 6 and 10. This is twice as big as the smallest triangle, so the base BD must be 6 × 2 =12, which is (C).
12. CUse SOHCAHTOA and your calculator to find the height of the flagpole. From the 70° angle, you know the adjacent side of the triangle, and you want to find the opposite side, so you need to use tangent. Tangent 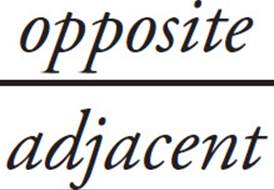 , so tan 70⁰ =
, so tan 70⁰ = 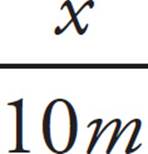 , where x is the height of the flagpole up to the ball. Isolate x by multiplying both sides by 10: 10 tan 70° = x. Use your calculator to find that 10 tan 70° = 27.47, which is closest to (C).
, where x is the height of the flagpole up to the ball. Isolate x by multiplying both sides by 10: 10 tan 70° = x. Use your calculator to find that 10 tan 70° = 27.47, which is closest to (C).
26. DDon’t forget that you can plug in numbers on geometry questions. Let’s make b = 70° and a = 30°. So the third angle in the triangle is 80°. You know that c would be 80°, because it is opposite an 80° angle. Your target answer is a = 30°, so plug in 80° and 70° to find it. The only possible answer is (D).
28. BThere’s a lot going on in this problem! But if we take it piece by piece, we’ll crack it. Let’s start filling in some information. The first thing the problem tells us is that triangle ABC is equilateral. Mark 60 degree angles on the figure. Next, we see that angle AEF is a right angle. Write that in as well. The problem also conveniently tells us that D and F are the midpoints of AB and AC, respectively. Therefore, AD and AF are 2. Finally, the last piece of information reveals that E is the midpoint of DF; mark DE and EF as equal.
Now, what do we have? Triangle AEF is a right triangle, with a hypotenuse of 2 and a leg of 1. Hmm, perhaps the good ol’ Pythagorean theorem can help us. Plug the numbers into the theorem, and you’ll see that the answer is (B).
You may have also noticed that triangle ADE is a 30°-60°-90° triangle with hypotenuse 2, which means that DE is 1 and w, opposite the 60°, is the square root of 3. In geometry questions on the SAT, there will often be multiple ways to get to the answer. On the day of the test, use whichever way you are most comfortable with.
29. BWork the problem in steps. You are given the mass, so to find density you need to find the volume of the pyramid. The formula at the beginning of the section tells you that, for a pyramid, V = ![]() Bh, where B is the area of the base of the pyramid and h is the height. Therefore, the volume of the pyramid is
Bh, where B is the area of the base of the pyramid and h is the height. Therefore, the volume of the pyramid is ![]() (15)(4) = 20. However, you need to subtract the volume of the semispherical indentation in the base. Once again, the reference sheet found beginning of the Math section tells you that the volume of a sphere is given by the equation V =
(15)(4) = 20. However, you need to subtract the volume of the semispherical indentation in the base. Once again, the reference sheet found beginning of the Math section tells you that the volume of a sphere is given by the equation V = ![]() πr3. Because the diameter of the indentation is 2 cm, the radius of the hemisphere is 1 cm. If it were a whole sphere, the volume of the indentation would be
πr3. Because the diameter of the indentation is 2 cm, the radius of the hemisphere is 1 cm. If it were a whole sphere, the volume of the indentation would be ![]() π(1)3 = 4.189; you want only half, so dividing by 2 gives you 2.094 cm3 for the hemisphere. Subtracting 2.094 cm3 from the 20 cm3 of the pyramid gives you a total volume of 20 − 2.094 = 17.906 cm3. Finally, you can find the density of Lucite by using the definition of density: Density =
π(1)3 = 4.189; you want only half, so dividing by 2 gives you 2.094 cm3 for the hemisphere. Subtracting 2.094 cm3 from the 20 cm3 of the pyramid gives you a total volume of 20 − 2.094 = 17.906 cm3. Finally, you can find the density of Lucite by using the definition of density: Density = 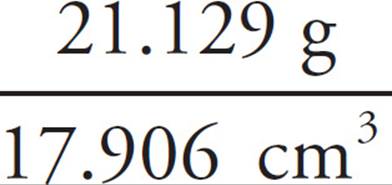 ≈ 1.18 g/cm3, which is (B).
≈ 1.18 g/cm3, which is (B).
Summary
○Degrees and angles:
•A circle contains 360 degrees.
•When you think about angles, remember circles.
•A line is a 180-degree angle.
•When two lines intersect, four angles are formed; the sum of their measures is 360 degrees.
•When two parallel lines are cut by a third line, the small angles are equal, the big angles are equal, and the sum of a big angle and a small angle is 180 degrees.
○Triangles
•Every triangle contains 180 degrees.
•An isosceles triangle is one in which two of the sides are equal in length, and the two angles opposite the equal sides are equal in measure.
•An equilateral triangle is one in which all three sides are equal in length, and all three angles are equal in measure (60 degrees).
•The area of a triangle is ![]() bh.
bh.
•The height must form a right angle with the base.
•The Pythagorean theorem states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. Remember ETS’s favorite Pythagorean triplets (3-4-5 and 5-12-13).
•Remember the other special right triangles: 45°-45°-90° and 30°-60°-90°.
•Similar triangles have the same angles and their lengths are in proportion.
•For trigonometry questions, remember SOHCAHTOA:
•sin = 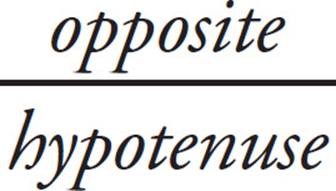
•cos = 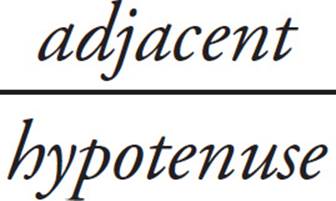
•tan = 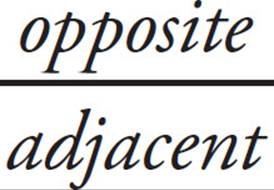
○Circles:
•The circumference of a circle is 2πr or πd, where r is the radius of the circle and d is the diameter.
•The area of a circle is πr2, where r is the radius of the circle.
•A tangent touches a circle at one point; any radius that touches that tangent forms a 90-degree angle.
•Arcs are proportional to the circumference based on the central angle: 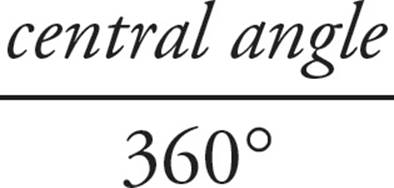 =
= 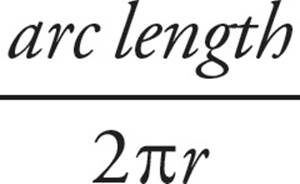 .
.
•Sectors are proportional to the area based on the central angle: 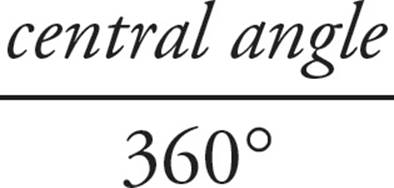 =
= 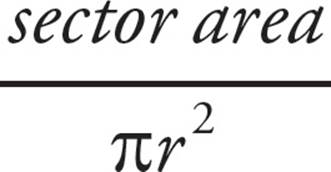 .
.
•If the central angle is given in radians, the measure of the arc is given by s = rθ.
○Rectangles and squares:
•The perimeter of a rectangle is the sum of the lengths of its sides.
•The area of a rectangle is length × width.
•A square is a rectangle whose four sides are all equal in length.
•Any polygon can be divided into triangles.
•The volume of a rectangular solid is length × width × height. The formulas to compute the volumes of other three-dimensional figures are supplied in the instructions at the front of both Math sections.
○When you encounter a geometry problem on the SAT, ballpark the answer before trying to work it out.
○You must be familiar with the size of certain common angles.
○Most SAT geometry diagrams are drawn to scale. Use your eyes before you use your pencil. Try to eliminate impossible answers.
○When a diagram is not drawn to scale, redraw it.
○When no diagram is provided, make your own; when a provided diagram is incomplete, complete it.
○When information is missing from a diagram, Ballpark and Plug In.