Cracking the New SAT with 4 Practice Tests, 2016 Edition (2015)

Part IV. How to Crack the Math Test

Chapter 17. Grid-Ins

On the SAT, 13 of the 58 Math questions will require you to produce your own answer. Although the format of these questions is different from that of the multiple-choice questions, the mathematical concepts tested aren’t all that different. In this chapter, we will show you how to apply what you have learned in the previous chapters to these new questions.

WHAT IS A GRID-IN?

Both of the Math sections on your SAT will contain a group of problems without multiple-choice answers. There will be 5 of these in the No Calculator section and 8 in the Calculator section. ETS calls these problems “student-produced responses.” We call them Grid-Ins because you have to mark your answers on a grid printed on your answer sheet. The grid looks like this:

Despite their format, grid-ins are just like any other Math questions on the SAT, and many of the techniques that you’ve learned so far still apply. You can still use Plugging In and other great techniques, such as the Ratio Box and Average Pie. Your calculator will still help you out on many problems as well. So grid-ins are nothing to be scared of. In fact, many of these are simply regular SAT multiple-choice math problems with the answer choices lopped off. The only difference is that you have to arrive at your answer from scratch rather than choose from four possibilities.

You will need to be extra careful with answering Grid-In questions, however, because the grid format increases the likelihood of careless errors. It is vitally important that you understand how the Grid-In format works before you take the test. In particular, you’ll need to memorize ETS’s rules about which kinds of answers count and which do not. The instructions may look complicated, but we’ve boiled them down to a few rules for you to memorize and practice.

Take a look at the grid again. Because of the way it’s arranged, ETS can use only certain types of problems for Grid-Ins. For example, you’ll never see variables (letters) in your answer (though there can be variables in the question) because the grids can accommodate only numbers. You will also never have a π, square root, or negative number in your answer. Most answers for Grid-Ins are integers.

Order of Difficulty:
Grid-Ins

As with the multiple-choice
questions, Grid-Ins
will be in a loose order
of difficulty.

Also, this means that your calculator will be useful on several questions. As always, be careful to set up the problem on paper before you carefully punch the numbers into your calculator. Because you have to write in the answer on the grid yourself, you need to be more careful than ever to avoid careless mistakes.

Just as with the multiple-choice questions, there is no penalty for wrong answers on the Grid-Ins. An incorrect answer on one of these questions is no worse for your score than a question left blank. And, by the same token, a blank is just as costly as an error. Therefore, you should be very aggressive in answering these questions. Don’t leave a question blank just because you’re worried that the answer you’ve found may not be correct. ETS’s scoring computers treat incorrect answers and blanks like they’re exactly the same. If you have arrived at an answer, you have a shot at earning points; and if you have a shot at earning points, you should take it.

Take a Guess

Just like the multiple-choice
questions, there
is no penalty for wrong
answers on the Grid-In
questions.

We’re not saying you should guess blindly. But if you work a problem and are unsure of your answer, enter it anyway. There is no penalty for getting it wrong.

THE INSTRUCTIONS

Here are the instructions for the Grid-In section as they will appear in Section 3 on the SAT. The instructions for Section 4 will look just like this, except they will start “For questions 31–38…”

What the Instructions Mean

Of all the instructions on the SAT, these are the most important to understand thoroughly before you take the test. Pity the unprepared student who takes the SAT cold and spends 10 minutes of potential point-scoring time reading and puzzling over ETS’s confusing instructions. We’ve translated these unnecessarily complicated instructions into a few important rules. Make sure you know them all well.

Watch Out

Negatives, π, and %
cannot be gridded in! For a
Grid-In question involving
% or $, the SAT will tell
you to ignore the % or $
symbol. But negative
numbers, non-integer
square roots, and π can’t
be gridded in, so they’ll
never be an answer for
this type of problem.

Fill In the Boxes

Always write your answer in the boxes at the top of the grid before you darken the ovals below. Your written answers won’t affect the scoring of your test; if you write the correct answer in the boxes and grid in the wrong ovals, you won’t get credit for your answer (and you won’t be able to appeal to ETS). However, writing in the answers first makes you less likely to make an error when you grid in, and it also makes it easier to check your work.

Fill In the Ovals Correctly

As we just pointed out, you receive no credit for writing in the answer at the top of the grid. ETS’s computer cares only whether the ovals are filled in correctly. For every number you write into the grid, make sure that you fill in the corresponding oval.

Stay to the Left

Although you’ll receive credit no matter where you put your answer on the grid, you should always begin writing your answer in the far left column of the grid. This ensures that you will have enough space for longer answers when necessary. You’ll also cut down on careless errors if you always grid in your answers the same way.

Keep Left

No matter how many
digits are in your answer,
always start gridding in
the left-most column. That
way, you’ll avoid omitting
digits and losing points.

FRACTIONS OR DECIMALS: YOUR CHOICE

You can grid in an answer in either fraction or decimal form. For example, if your answer to a question is , you can either grid in or .5. It doesn’t matter to ETS because equals .5; the computer will credit either form of the answer. That means you actually have a choice. If you like fractions, grid in your answers in fraction form. If you like decimals, you can grid in the decimal. If you have a fraction that doesn’t fit in the grid, you can simply convert it to a decimal on your calculator or on paper and grid in the decimal.

Here’s the bottom line: When gridding in fractions or decimals, use whichever form is easier and least likely to cause careless mistakes.

Decimal Places and Rounding

When you have a decimal answer of a value less than 1, such as .45 or .678, many teachers ask you to write a zero before the decimal point (for example, 0.45 or 0.678). On Grid-In questions, however, ETS doesn’t want you to worry about the zero. In fact, there is no 0 in the first column of the grid. If your answer is a decimal less than 1, just write the decimal point in the first column of the grid and then continue from there.

Lop

Why do extra work for
ETS? After all, they won’t
give you extra points. If
your decimal doesn’t fit
in the grid, lop off the
extra digits and grid in
what does fit.

You should also notice that if you put the decimal point in the first column of the grid, you have only three places left to write in numbers. But what if your decimal is longer than three places, such as .87689? In these cases, ETS will give you credit if you round off the decimal so that it fits in the grid. But you’ll also get credit, however, if you just enter as much of the decimal as will fit.

For example, if you had to grid in .87689, you could just write .876 (which is all that will fit) and then stop. You need to grid in only whatever is necessary to receive credit for your answer. Don’t bother with extra unnecessary steps. You don’t have to round off decimals, so don’t bother.

If you have a long or repeating decimal, however, be sure to fill up all the spaces in the grid. If your decimal is .666666, you must grid in .666. Just gridding in .6 or .66 is not good enough.

Note: Very long decimal answers are somewhat rare. Your answer should usually be integers or simple fractions.

Reducing Fractions

If you decide to grid in a fraction, ETS doesn’t care if you reduce the fraction or not. For example, if your answer to a problem is , ETS will give you credit if you grid in or reduce it to . So if you have to grid in a fraction, and the fraction fits in the grid, don’t bother reducing it. Why give yourself more work (and another chance to make a careless error)?

Relax

If your answer is a fraction
and it fits in the grid
(fraction bar included),
don’t reduce it. Why
bother? ETS won’t give
you an extra point.
However, if your fraction
doesn’t fit, reduce it or
turn it into a decimal on
your calculator, depending
on the section you’re
working on.

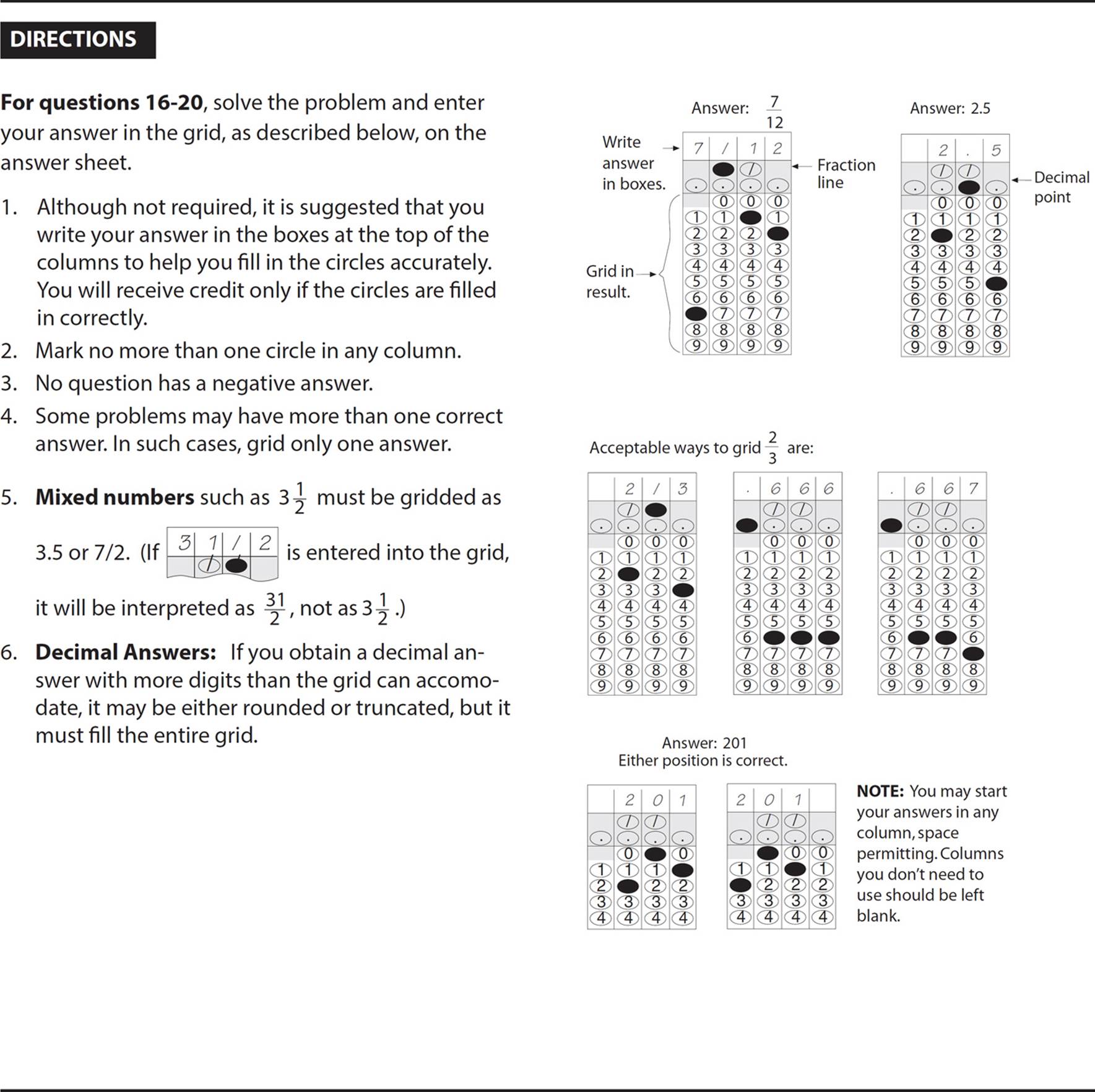
The only time you might have to reduce a fraction is if it doesn’t fit in the grid. If your answer to a question is 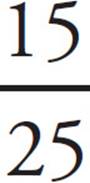, it won’t fit in the grid. You have two options: Either reduce the fraction to and grid that in, or use your calculator to convert the fraction to .6. Choose whichever process makes you the most comfortable when calculator use is allowed, and make sure you know how to reduce fractions for the No Calculator section.

Mixed Numbers

ETS’s scoring machine does not recognize mixed numbers. If you try to grid in 2 by writing “2 1/2,” the computer will read this number as 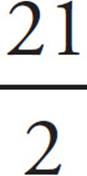. You have to convert mixed numbers to fractions or decimals before you grid them in. To grid in 2, either convert it to or its decimal equivalent, which is 2.5. If you have to convert a mixed number to grid it in, be very careful not to change its value accidentally.

Don’t Mix

Never grid in a mixed
number. Change it into a
top-heavy fraction or its
decimal equivalent.

Don’t Worry

The vast majority of Grid-In answers will not be difficult to enter in the grid. ETS won’t try to trick you by purposely writing questions that are confusing to grid in. Just pay attention to these guidelines and watch out for careless errors.

GRIDDING IN: A TEST DRIVE

To get a feel for this format, let’s work through two examples. As you will see, Grid-In problems are just regular SAT Math problems.

16.If a + 2 = 6 and b + 3 = 21, what is the value of ?

Here’s How to Crack It

You need to solve the first equation for a and the second equation for b. Start with the first equation, and solve for a. By subtracting 2 from both sides of the equation, you should see that a = 4.

Now move to the second equation, and solve for b. By subtracting 3 from both sides of the second equation, you should see that b = 18.

The question asked you to find the value of . That’s easy. The value of b is 18, and the value of a is 4. Therefore, the value of is .

That’s an ugly-looking fraction. How in the world do you grid it in? Ask yourself this question: “Does 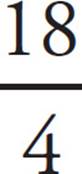fit?” Yes! Grid in .

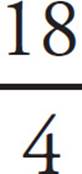Your math teacher wouldn’t like it, but ETS’s computer will. You shouldn’t waste time reducing 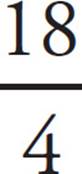to a prettier fraction or converting it to a decimal. Spend that time on another problem instead. The fewer steps you take, the less likely you will be to make a careless mistake.

Here’s another example. This one is quite a bit harder.

34.Forty percent of the members of the sixth-grade class wore white socks. Twenty percent wore black socks. If twenty-five percent of the remaining students wore gray socks, what percent of the sixth-grade class wore socks that were not white, black, or gray? (Disregard the % when gridding your answer.)

Here’s How to Crack It

The problem doesn’t tell you how many students are in the class, so you can plug in any number you like. This is a percentage problem, so the easiest number to plug in is 100. Forty percent of 100 is 40; that means 40 students wore white socks. Twenty percent of 100 is 20. That means that 20 students wore black socks.

Your next piece of information says that 25 percent of the remaining students wore gray socks. How many students remain? Forty, because 60 students wore either white or black socks, and 100 − 60 = 40. Therefore, 25 percent of these 40—10 students—wore gray socks.

How many students are left? 30. Therefore, the percentage of students not wearing white, black, or gray socks is 30 out of 100, or 30 percent. Grid it in, and remember to forget about the percent sign.

ORDER OF DIFFICULTY

Like all other questions on the Math Test, Grid-In problems are arranged in a loose order of difficulty. Since this order is not strict, however, it is much more important to pay attention to your own strengths and weaknesses. Remember to focus on the questions you know how to answer first. Don’t spend time on questions that you have no idea how to work.

Keep in mind, of course, that many of the math techniques that you’ve learned are still very effective on Grid-In questions. Plugging In worked very well on the previous question. If you’re able to plug in or take an educated guess, go ahead and grid in that answer. Again, there is no penalty for getting it wrong.

Here’s another difficult Grid-In question that you can answer effectively by using a technique you’ve learned before:

36.Grow-Up potting soil is made from only peat moss and compost in a ratio of 3 pounds of peat moss to 5 pounds of compost. If a bag of Grow-Up potting soil contains 12 pounds of potting soil, how many pounds of peat moss does it contain?

Here’s How to Crack It

To solve this problem, set up a Ratio Box.

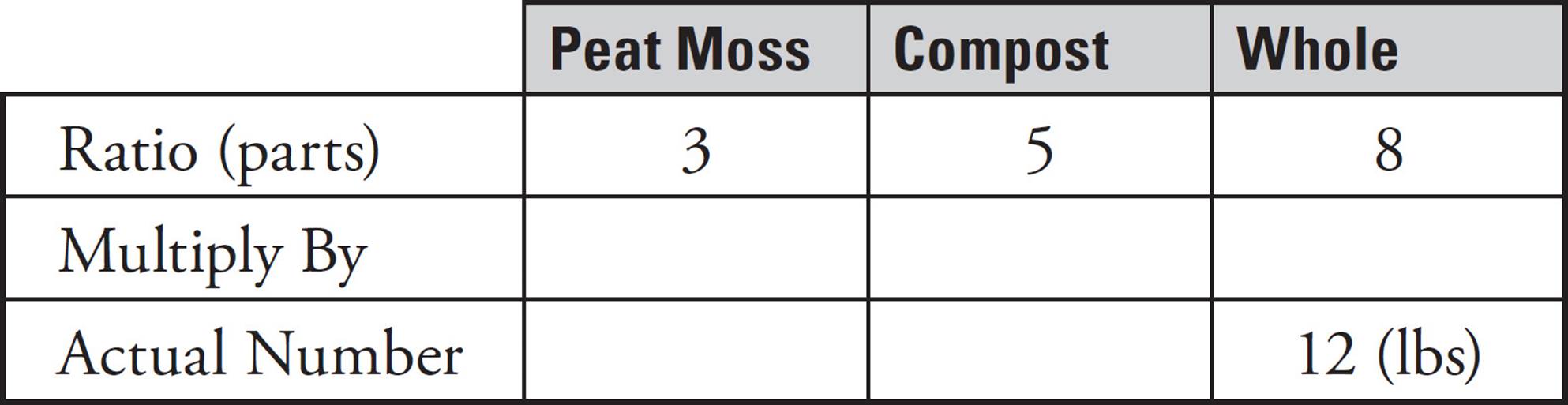
What do you multiply by 8 to get 12? If you don’t know, divide 12 by 8 on your calculator. The answer is 1.5. Write 1.5 in each of the boxes on the multiply by row of your Ratio Box.

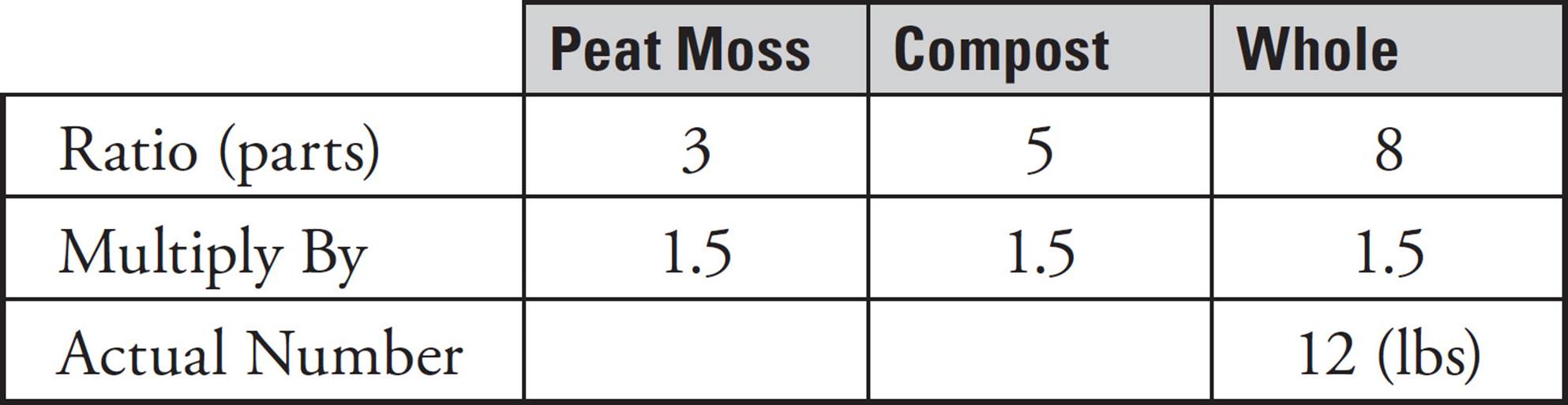
The problem asks you how many pounds of peat moss are in a bag. To find out, multiply the numbers in the Peat Moss column. That is, multiply 3 × 1.5, and you get 4.5. ETS’s answer is 4.5.

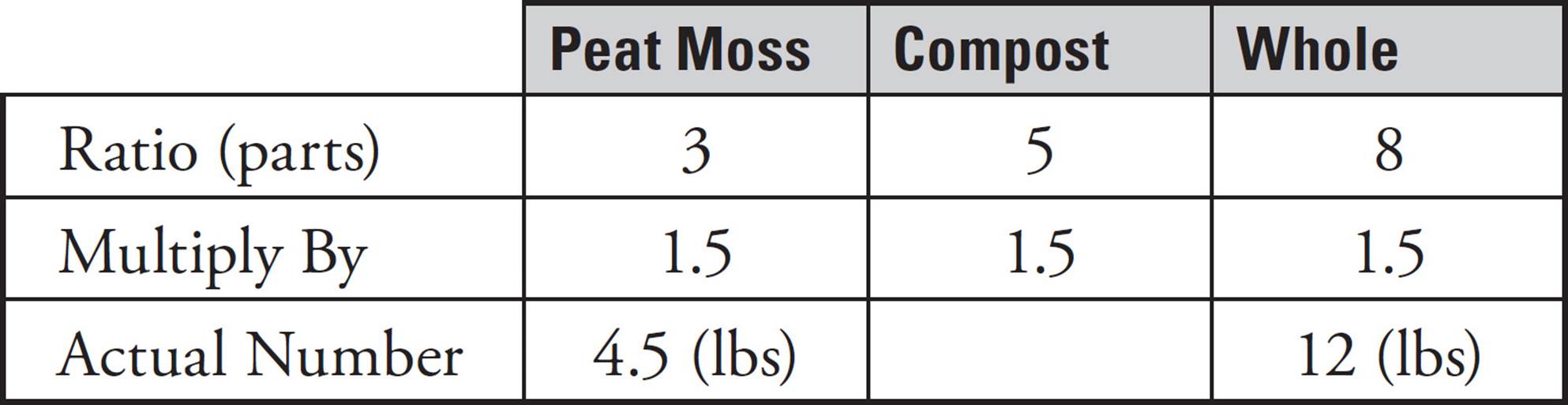
Grid it in like this:

Careless Mistakes

On Grid-In questions, you obviously can’t use Process of Elimination to get rid of bad answer choices, and techniques like Plugging In the Answers won’t work either. In order to earn points on Grid-In questions, you’re going to have to find the real answers, and you’re going to have to be extremely careful when you enter your answers on your answer sheet. If you need to, double-check your work to make sure you have solved correctly. If you suspect that the question is a difficult one and you get an answer too easily, you may have made a careless mistake or fallen into a trap.

RANGE OF ANSWERS

Some Grid-In problems will have many possible correct answers. It won’t matter which correct answer you choose, as long as the one you choose really is correct.

More Than One

Some Grid-In questions
have several possible
correct answers. None
is more correct than any
other, so grid in the first
one you find and move on.

Here’s an example:

17.If 4 < 3x + 2 < 5, what is one possible value of x ?

Here’s How to Crack It

With double inequalities or equations, don’t try to do the entire problem at once. It’s much easier to split this problem into two smaller problems:

4 < 3x + 2 and 3x + 2 < 5

Solve each one. For the first inequality, start by subtracting 2 from both sides, leaving 2 < 3x. Divide by 3, leaving (approximately) 0.666 < x. For the other inequality, start, as before, by subtracting 2 from both sides, leaving 3x < 3. Divide by 3 to get x < 1. Combining both inequalities back together, you’ll get that x is between 0.666 and 1.

So, what do you enter as your answer? Anything between .666 and 1. Really. Anything. .8, .954, .667, .999, 5/6, 7/8, 9/10, whatever.

EXTENDED THINKING

The last two questions in Section 4 (calculator allowed) will be a pair of Grid-Ins that ETS refers to as Extended Thinking questions. It claims that these questions, drawn from real-world contexts, will assess a student’s ability to apply “complex cognitive skills.” Don’t panic, though. Aside from being paired and sometimes more difficult, they are not any different than other Grid-Ins. Many of the same strategies will apply to the Extended Thinking questions. They can be drawn from pretty much any mathematical content, from problem solving to functions, and they are only worth one point each.

Extended What?

The last two Grid-Ins will
be a pair of questions
based on the same information.
They can cover
any of the previous math
content, and they are still
worth just one point each.
Use your knowledge of
your own test-taking skills
to decide which of these
you want to try, if you do
them at all.

Let’s look at a set.

Questions 37 and 38 refer to the following information.

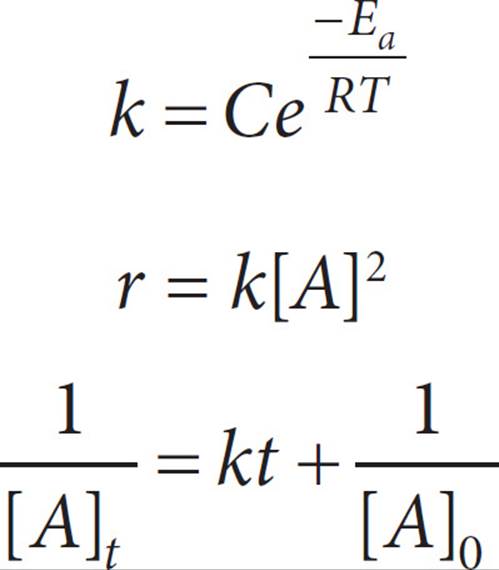
The kinetics of a chemical reaction can be described by the equations above, where e is a constant approximately equal to 2.718, k is the rate constant in L/mol-s, E_a is the activation energy in J/mol-K, T is temperature in Kelvin, r is the reaction rate in mol/s, and [A] is the concentration of a species in mols/L, either initially as [A]₀, or at a given time of t as [A]_t. C is a constant equal to 4, and R is a constant of 8.314 J/mol.

37.If the reaction initially starts with 2 mols/L of species A, and the activation energy of the reaction is 10,082 J/mol, at 310 Kelvin, how many seconds will it take for the concentration of A to reach 0.4 mols/L?

38.If rate constant k triples for the reaction described in question 37, what is the concentration of species A after 50 seconds, in mols/L?

Here’s How to Crack It

As you can see, in order to have a chance at solving question 38, you first must solve question 37. In most cases, the two Extended Thinking questions will be more independent of each other. In that case, if one is easier than the other, maybe try that one and skip the other one. Only students aiming for a top score should attempt both Extended Thinking questions.

Tackling Extended
Thinking Questions

Most Extended Thinking
questions can be solved
independent of one
another, and one is often
easier than the other.
Consider doing the more
straightforward one and
skipping the more difficult
or time-consuming one.

Let’s start with question 37. There are three equations, so it is hard to know where to begin. Start by writing down the values for the variables you know. The question tells us that [A]₀ = 2 and [A]_t = 0.4. You want to find the time, t, so plug these values into the last equation to get 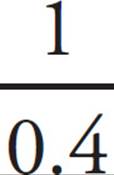= kt + . Simplify this equation to get 2.5 = kt + 0.5, and kt = 2. To solve for t, you first need to figure out the value of k. You need to use the first equation to find the value of k, since the value of r in the second equation is never defined. According to the question, C and R are constants, where C = 4 and R = 8.314. Also according to the question, E_a = 10,082, and T = 310. Plug all of these values into the first equation to get k = 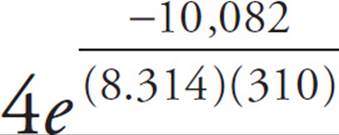. Simplify the exponent to get k = 4e^−3.9118. Use your calculator to find that k = 4(0.02) = 0.08. Plug this value into the earlier equation kt = 2 to get 0.08t = 2, and t = 25. The correct answer is 25. Grid it in!

Notice how the second equation was completely useless in solving this problem. That will happen occasionally on the SAT, so don’t get distracted by the extraneous information.

Now that we have the value of rate constant k, let’s crack question 38. In question 37, k = 0.08, so if k triples, the new value for k is 0.08 × 3 = 0.24. According to the information in question 37, [A]₀ = 2, and according to question 38, t = 50. Plug all of these values into the last equation, which has [A]_t in it, to get 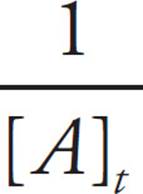= (0.24)(50) + . Simplify the right side of the equation to get 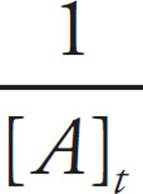= 12.5. Multiply both sides by [A]_tto get 1 = 12.5[A]_t. Finally, divide both sides by 12.5 to get. The correct answer is 0.08 = [A]_t. The correct answer is 0.08.

Grid-In Drill 1: No Calculator Section

Work these Grid-Ins without your calculator using the skills you’ve learned so far. Answers and explanations can be found on this page.

16.If a^b = 4, and 3b = 2, what is the value of a ?

17.4x + 2y = 24 and 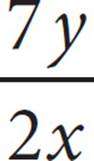= 7, what is the value of x ?

18.If 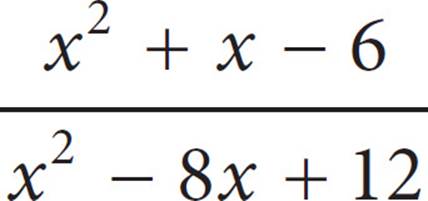= 4, what is the value of x ?

19.If −1 ≤ a ≤ 2 and −3 ≤ b ≤ 2, what is the greatest possible value of (a + b)(b − a) ?

Grid-In Drill 2: Calculator-Permitted Section

Work these Grid-Ins using your calculator as needed and applying the skills you’ve learned so far. Answers and explanations can be found on this page.

32.

n = 12 ×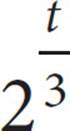

The number of mice in a certain colony is shown by the formula above, such that n is the number of mice and t is the time, in months, since the start of the colony. If 2 years have passed since the start of the colony, how many mice does the colony contain now?

33.

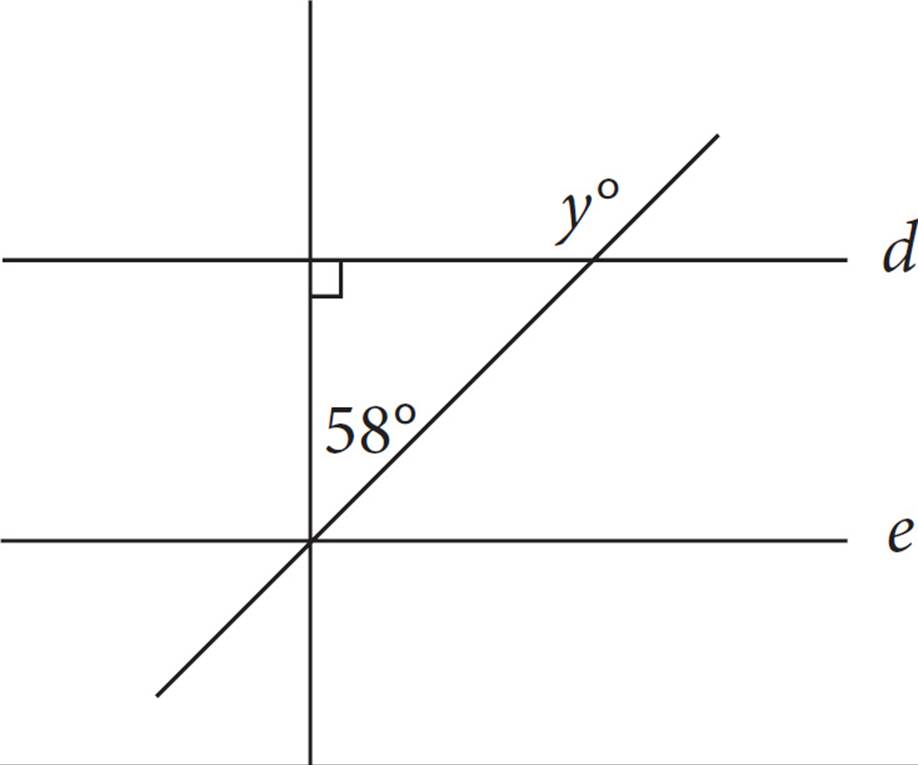
In the figure above, if d is parallel to e, what is the value of y ?

35.If Alexandra pays $56.65 for a table, and this amount includes a tax of 3% on the price of the table, what is the amount, in dollars, that she pays in tax? (Disregard the dollar sign when gridding your answer.)

36.

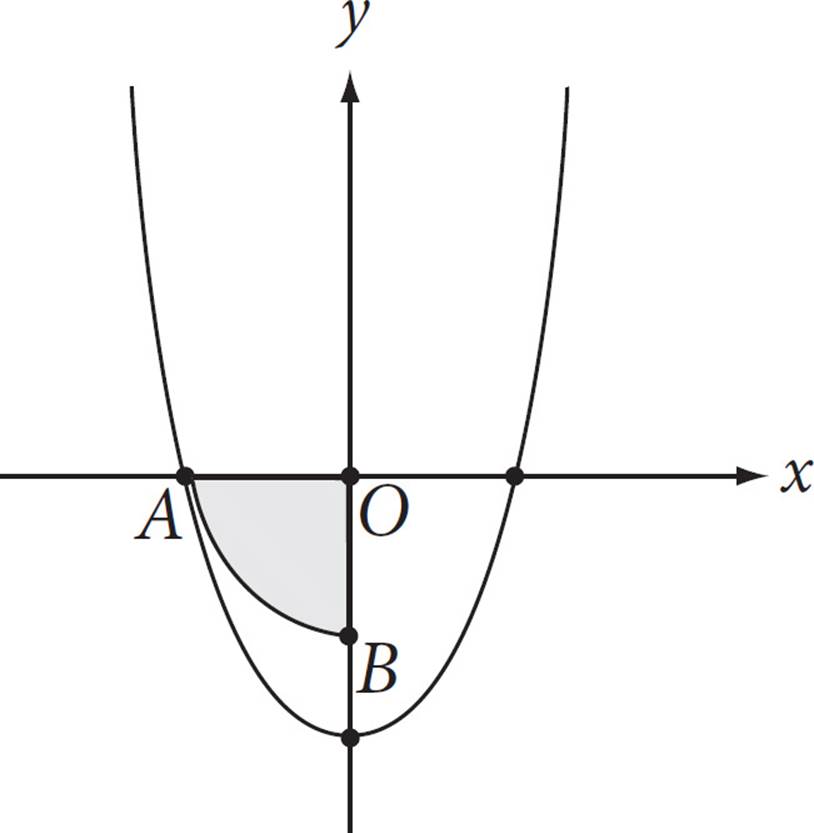
In the figure above, AB is the arc of the circle with center O. Point A lies on the graph of y = x² − b, where b is a constant. If the area of shaded region AOB is π, then what is the value of b ?

Questions 37 and 38 refer to the following information.

A garden, measuring 10 feet by 12 feet, contains individual plots that measure 1 foot by 1 foot. 30% of the plots contain bell peppers, 30% contain cherry tomatoes, 25% contain squash, and the remaining 15% contain eggplants. Each bell pepper plot produces 2 bell peppers every 5 days, a tomato plot produces 4 cherry tomatoes every 6 days, a squash plot produces 1 squash every 15 days, and an eggplant plot produces 3 eggplants every 10 days.

37.In a 30-day month, how many vegetables are produced by the 10 × 12 foot garden?

38.An unusually warm and wet month causes the monthly production of eggplants to double. What is the daily average number of eggplants produced in the garden during a 30-day month at the new rate?

CHAPTER DRILL ANSWERS AND EXPLANATIONS

Geometry Drill 1: No Calculator Section

16. 8Using 3b = 2, solve for b by dividing both sides by 3 to get b = . That means 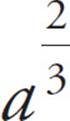= 4. Fractional exponents tell you to use the denominator as the root and use the numerator as a regular exponent. So, 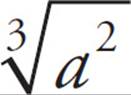= 4. First, cube both sides to find a² = 4³ = 64. Next, take the square root of both sides to find a = 8.

17. 3You can solve this question using simultaneous equations because you have two equations with two variables. First, you need to rearrange the equations a bit: 4x + 2y = 24 divided by 2 on both sides becomes 2x + y = 12. 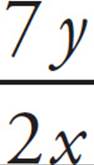= 7, multiplied by 2x on both sides, becomes 7y = 14x. This, divided by 7 on both sides, becomes y = 2x, which can be manipulated into 2x − y = 0. Now you can add the equations:

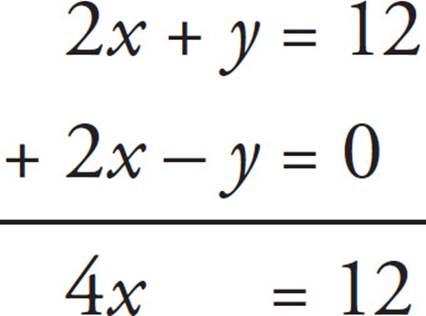
So x = 3.

18. 9Factor the numerator and the denominator into 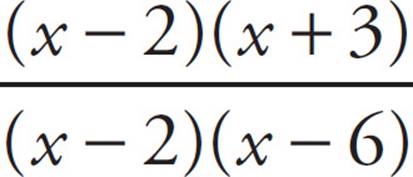= 4. The (x − 2) cancels out of the top and bottom to leave 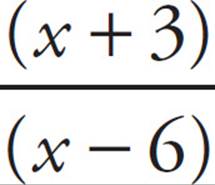= 4. Multiply both sides by (x − 6) to get x + 3 = 4x − 24. Subtract x from both sides: 3 = 3x − 24. Add 24 to both sides: 27 = 3x. Divide by 3 to get x = 9.

19. 9This looks suspiciously like a quadratic equation, and if you multiply it out, its equivalent is b² − a². You want to make this as large as possible, so you want b² to be large and a² to be small. If b = −3, b² = 9; if a = 0, a² = 0. So b² − a² can be as large as 9.

Grid-In Drill 2: Calculator-Permitted Section

32. 3,072
Because the t in n = 12 × 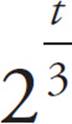represents the number of months, we cannot use the 2 years time frame given in the question in place of t. The colony has been growing for 24 months, which is evenly divisible by the 3 in the fractional exponent. The equation is much easier now that the fractional exponent is gone. n = 12 × 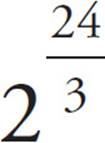= 12 × 2⁸ = 12 × 256 = 3,072.

33. 148A line crossing two parallel lines creates big angles and small angles. The big angle that matches y is split by a line perpendicular to d and e. The big angle is 58 + 90 = 148, which is also the value for y. Another way to solve this is to find the third angle of the triangle: 180 − 90 − 58 = 32. The 32° angle and the y° angle make up a straight line, so 180 − 32 = 148.

35. 1.65The best way to approach this problem is to set up an equation. There is some price such that if you add 3% of the price to the price itself, you get $56.65. This means that you can set up an equation: x+ 3% of x = 56.65, or x + 0.03x = 56.65. Now you can just solve for x, and you get the original price, which was $55. Subtract this from $56.65 to get the tax $1.65.

36. 4This question looks tough, so work it one step at a time, and start with what you know. Sector AOB is a quarter-circle (it covers an angle of 90 out of 360 degrees), so multiplying its area (π) by 4 gives you the area of the whole circle (4π). Plugging this into the equation for the area of a circle, A = πr², gives you 4π = πr², and the radius must be a positive value, so r = 2. This means that the coordinates of point A must be (−2, 0). Because A is on both the circle and the parabola, you can plug its x- and y-coordinates into the given equation of the parabola, y = x² − b. This becomes 0 = (−2)² − b, so b = 4.

37.1,374

First, calculate the number of plots in the garden. Given that the garden measures 10 feet by 12 feet and each plot is one foot by one foot, there are 10 × 12 = 120 total plots. Next calculate the number of each type of vegetable plot as follows:

120 × 0.3 = 36 bell pepper plots

120 × 0.3 = 36 cherry tomato plots

120 × 0.25 = 30 squash plots

120 × 0.15 = 18 eggplant plots

According to the question, 2 bell peppers are grown every 5 days on each of the 36 pepper plots. That means that all the pepper plots together grow 2 × 36 = 72 peppers in 5 days. To determine how many peppers would grow in a month, set up a proportion.

=

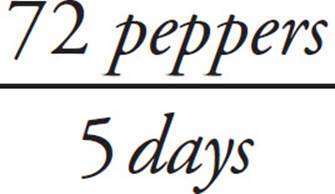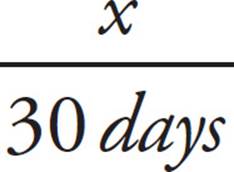
Cross-multiply, and then divide by 5 to find that the garden produces 432 peppers for the month. Repeat these steps with the other 3 vegetables. The 36 tomato plots produce 144 tomatoes every 6 days. Together, they produce 720 tomatoes in the month. The 30 squash plots produce 30 squash every 15 days, for a total of 60 squash in a month. Finally the 18 eggplant plots grow 54 eggplants every 10 days, which means during a 30-day period the garden will produce 162 eggplants. The total number of vegetables can be calculated as 432 bell peppers + 720 cherry tomatoes + 60 squash + 162 eggplants = 1,374 vegetables.

38. 10.8During a normal month, each eggplant plot produces 3 eggplants every 10 days. Therefore, if the production were to double, each plot would produce 6 eggplants every 10 days. Given that the garden measures 10 feet by 12 feet and each plot is one foot by one foot, there are 10 × 12 = 120 total plots, 15% of which are eggplant plots. Therefore, there are 120 × 0.15 = 18 eggplant plots. Calculate the total number of eggplants produced in 10 days as 18 × 6 = 108. In a 30-day month, there are three 10-day periods, so the entire garden would produce 108 × 3 = 324 total eggplants. To find the daily average production, divide 324 by 30 to get an average of 10.8 eggplants each day.

Summary

○Both of the Math sections on your SAT will contain a group of problems without multiple-choice answers. ETS calls these problems “Student-Produced Responses.” We call them Grid-Ins, because you have to mark your answers on a grid printed on your answer sheet.

○Despite their format, Grid-Ins are really just like other Math questions on the SAT, and many of the same techniques that you have learned still apply.

○The grid format increases the likelihood of careless errors. Know the instructions and check your work carefully.

○Just like the rest of the exam, there is no guessing penalty for Grid-Ins, so you should always grid in your answer, even if you’re not sure whether it’s correct.

○Always write the numbers in the boxes at the top of the grid before you (carefully) fill in the corresponding ovals.

○Grid in your answer as far to the left as possible.

○If the answer to a Grid-In question contains a fraction or a decimal, you can grid in the answer in either form. When gridding in fractions or decimals, use whichever form is easier and least likely to cause careless mistakes.

○There’s no need to round decimals, even though it is permitted.

○If you have a long or repeating decimal, be sure to fill up all the spaces in the grid.

○If a fraction fits in the grid, you don’t have to reduce the fraction before gridding it in.

○ETS’s scoring computer does not recognize mixed numbers. Convert mixed numbers to fractions or decimals before gridding them in.

○Some Grid-In questions will have more than one correct answer. It doesn’t matter which answer you grid in, as long as it’s one of the possible answers.

○Like all other questions on the SAT Math Test, Grid-In problems are arranged in a loose order of difficulty. Use your knowledge of your own strengths and weaknesses to decide which ones to tackle first and which ones, if any, to skip.

○The last two Grid-Ins in Section 4 are Extended Thinking questions, a set of questions on the same information. Usually, they can be answered independently, and they are worth only 1 point each. Attempt both only if you are aiming for a top score.

○Negatives, π, square roots, %, and degree symbols cannot be gridded in.