GRE Premier 2017 with 6 Practice Tests
Part III. QUANTITATIVE REASONING
Chapter 14. Quantitative Reasoning Practice Sets
In this chapter, you will take three practice sections, composed of 20 questions each. A diagnostic tool is provided after each section to help you learn from your mistakes. Then you can continue to the next set with more awareness of the traps you may encounter.
Review of the Kaplan Methods for Quantitative Reasoning Question Types
Before starting your practice sets, review the steps and strategies you have studied for answering each type of Quantitative Reasoning question quickly, efficiently, and correctly before starting your Practice Sets.
The Kaplan Method for Quantitative Comparison
1. STEP 1Analyze the centered information and quantities.
2. STEP 2Approach strategically.
The Kaplan Method for Problem Solving
1. STEP 1Analyze the question.
2. STEP 2Identify the task.
3. STEP 3Approach strategically.
4. STEP 4Confirm your answer.
The Kaplan Method for Data Interpretation
1. STEP 1Analyze the tables and graphs.
2. STEP 2Approach strategically.
Quantitative Reasoning Practice Set 1
Numbers
All numbers are real numbers.
Figures
The position of points, lines, angles, and so on may be assumed to be in the order shown; all lengths and angle measures may be assumed to be positive.
Lines shown as straight may be assumed to be straight.
Figures lie in the plane of the paper unless otherwise stated.
Figures that accompany questions are intended to provide useful information. However, unless a note states that a figure has been drawn to scale, you should solve the problems by using your knowledge of mathematics, not by estimation or measurement.
Directions
Each of the following questions, 1–8, consists of two quantities, Quantity A and Quantity B. You are to compare the two quantities and choose
1. if Quantity A is greater
2. if Quantity B is greater
3. if the two quantities are equal
4. if the relationship cannot be determined from the information given
·
Common Information
In a question, information concerning one or both of the quantities to be compared is centered above the two quantities. A symbol that appears in both quantities represents the same thing in Quantity A as it does in Quantity B.
1.
2.
1.
1.
|
Quantity A |
Quantity B |
|
The number of distinct ways to form an ordered line of 3 people by choosing from 6 people |
The number of distinct ways to form an unordered group of 3 people by choosing from 10 people |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
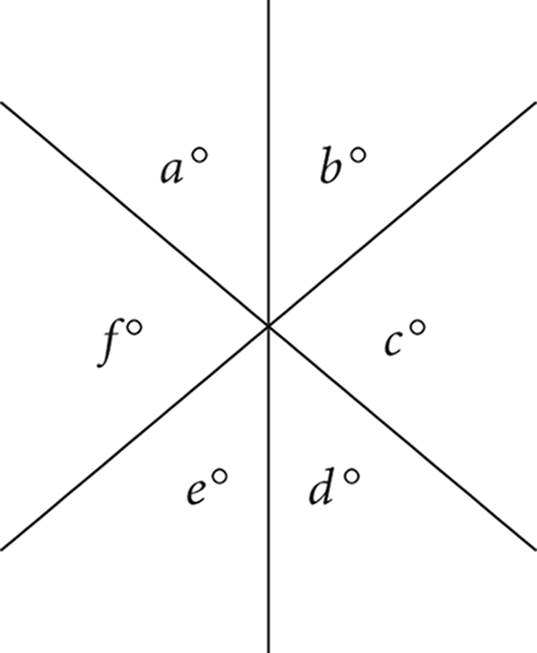
2. 
2.
|
Quantity A |
Quantity B |
|
a + c + e |
b + d + f |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
3. 7p + 3 = r
3p + 7 = s
3.
|
Quantity A |
Quantity B |
|
r |
s |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
4. The original cost of a shirt is x dollars.
|
Quantity A |
Quantity B |
|
x |
The cost of the shirt if the original cost is first increased by 10% and then decreased by 10% |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
5. There were x dictionaries in a bookstore. After ![]() of them were purchased, 10 more dictionaries were shipped in, bringing the total number of dictionaries to 52.
of them were purchased, 10 more dictionaries were shipped in, bringing the total number of dictionaries to 52.
|
Quantity A |
Quantity B |
|
x |
50 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
There are n people in a room. One-third of them leave the room. Four people enter the room. There are now ![]() of the original number of people in the room.
of the original number of people in the room.
6.
|
Quantity A |
Quantity B |
|
n |
20 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
7. 
Note: Figure not drawn to scale.
7.
|
Quantity A |
Quantity B |
|
The perimeter of the figure, in meters |
16 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
8. x is an integer.
1 < x < 9
|
Quantity A |
Quantity B |
|
|
|
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
3.
8.
9. If ![]() and x + y = 15, which of the following is greater than y?
and x + y = 15, which of the following is greater than y?
Indicate all possible choices.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
10.The product of two integers is 10. Which of the following could be the average (arithmetic mean) of the two numbers?
Indicate all possible choices.
1. −5.5
2. −3.5
3. −1.5
4. 1.5
5. 3.5
11.Which of the following is greater than the sum of the distinct prime factors of 210?
Indicate all possible choices.
1. 12
2. 17
3. 19
4. 21
5. 24
12.The average (arithmetic mean) bowling score of n bowlers is 160. The average of these n scores together with a score of 170 is 161. What is the number of bowlers, n?
bowlers
13.Set T consists of five integers: the first five odd prime numbers when counting upward from zero. This gives set T a standard deviation of approximately 3.71. Which of the following values, if added to the set T, would increase the standard deviation of set T?
1. 11
2. 9
3. 7.8
4. 4.15
5. 3.7
14. 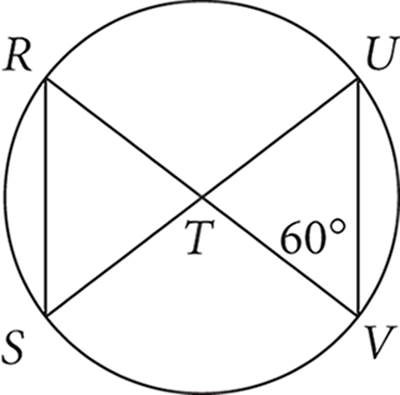
14.The circle shown has center T. The measure of angle TVU is 60°. If the circle has a radius of 3, what is the length of segment RS?
1. 2
2. ![]()
3. 3
4. ![]()
5. ![]()
15.What is the probability of rolling a total of 7 with a single roll of two fair six-sided dice, each with the distinct numbers 1–6 on each side?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
16.If it takes three days for 10 workers to finish building one house, how many days will it take 15 workers to finish four houses?
days
4.
16.
17. Questions 17–20 are based on the following graph and table.
18. 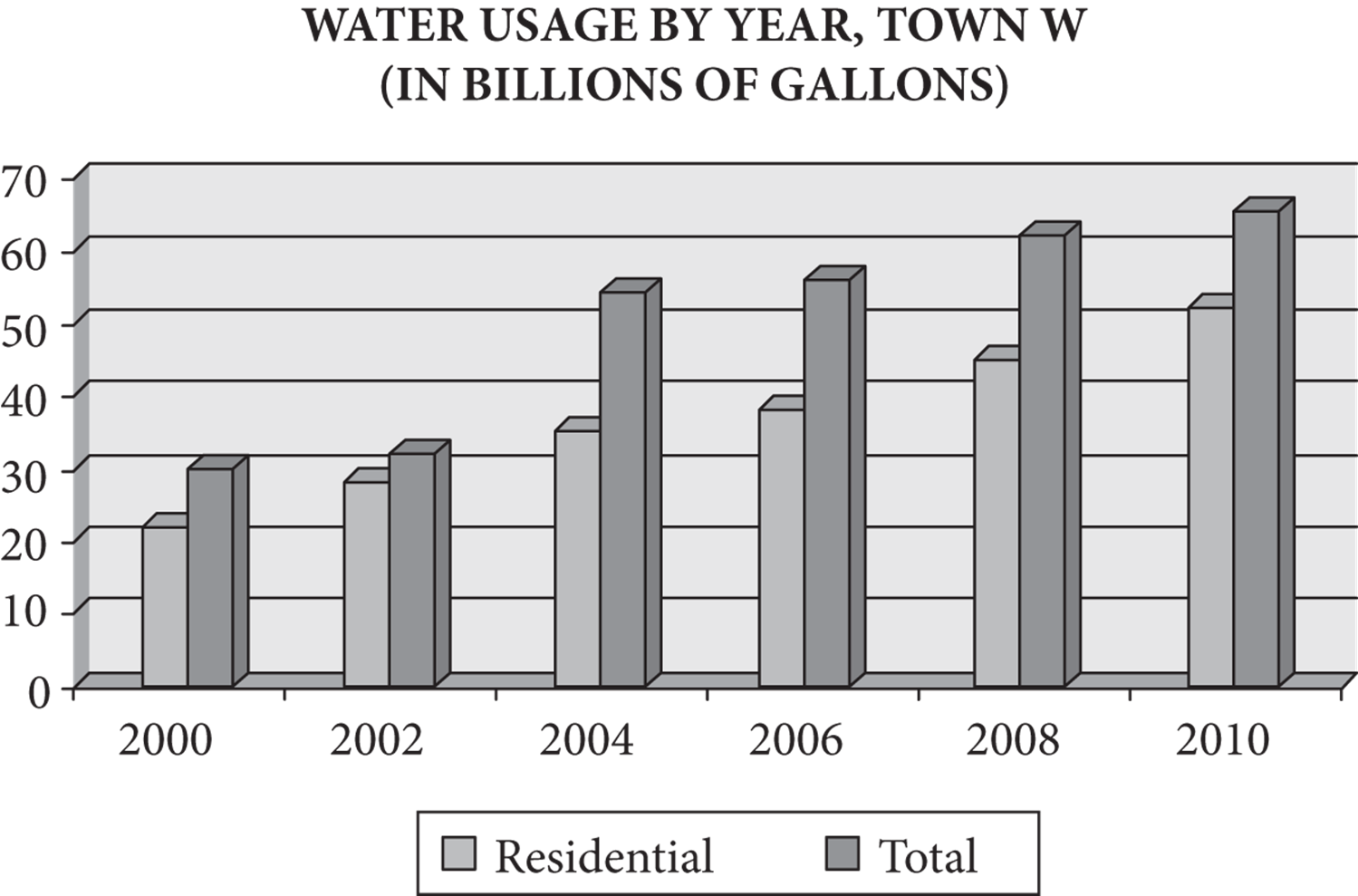 DAILY WATER USAGE STATISTICS (with efficient appliances and good maintenance)
DAILY WATER USAGE STATISTICS (with efficient appliances and good maintenance)
|
Use |
Gallons per Capita |
|
Showers |
9 |
|
Clothes washers |
10 |
|
Toilets |
8 |
|
Leaks |
4 |
|
Faucets |
11 |
|
Other |
4 |
19.
1.
17.Which best describes the range (in billions of gallons) for residential water consumption from 2000 to 2010, inclusive?
1. 10
2. 20
3. 30
4. 40
5. 50
18.In the year in which total usage exceeded residential usage by the least number of gallons, approximately what percent of total usage was residential usage?
1. 68%
2. 75%
3. 88%
4. 95%
5. 98%
19.In 2004, only 10,000 residents of town W lived in homes with efficient appliances and good maintenance. How many gallons per day were used by these residents for the three daily household purposes requiring the most water?
1. 110,000
2. 160,000
3. 270,000
4. 300,000
5. 460,000
20.Households with efficient appliances and good maintenance can reduce water consumption by about 35%. If half of the residential consumption in town W in 2010 was by households with efficient appliances and good maintenance, how many gallons of water (in billions) were saved that year?
1. 5
2. 14
3. 40
4. 52
5. 65
20.
Answer Key
QUANTITATIVE REASONING PRACTICE SET 1
1. C
2. C
3. D
4. A
5. B
6. A
7. C
8. A
9. B, C, D, E
10.A, B, E
11.C, D, E
12.9
13.E
14.C
15.B
16.8
17.C
18.C
19.D
20.B
Answers and Explanations
QUANTITATIVE REASONING PRACTICE SET 1
1. C
Quantity A is a permutation because order matters. The number of ways 3 people chosen from a group of 6 can be arranged in a line, where order matters, is 6 × 5 × 4 = 120.Quantity B is a combination because order does not matter. The number of ways 3 people can be selected from a group of 10, where order does not matter, is
![]()
The two quantities are equal.
2. CThere are three sets of vertical angles in this diagram: (a, d), (b, e), and (c, f). In Quantity A, you can substitute b for e because they are vertical angles and therefore equal; this leaves the sum a + b + c in Quantity A. Because these are the three angles on one side of a straight line, they sum to 180°. Similarly, after substituting e for b in Quantity B, b + d+ f is the same thing as d + e + f, or also 180°. The two quantities are equal.
3. DPick a value for p and see what effect it has on r and s. If p = 1, r = (7 × 1) + 3 = 10, and s = (3 × 1) + 7 = 10, and the two quantities are equal. But if p = 0, r = (7 × 0) + 3 = 3, and s = (3 × 0) + 7 = 7, and Quantity A is less than Quantity B. Because there are at least two different possible relationships, the answer is (D).
4. AUse the Picking Numbers strategy to answer this question. Suppose the original selling price of the shirt, x, is $100. After a 10% increase in price, the shirt would sell for 110% of $100, which is $110. If there is a 10% decrease next, the shirt would sell for 90% of the current price. That would be 90% of $110: 0.9 × $110 = $99. This price is less than the original amount, x, so Quantity A is greater.
5. BTry to set the quantities equal. If x is 50, then the bookstore started out with 50 dictionaries. Then ![]() of them were purchased. You can see already that the quantities can’t be equal, because
of them were purchased. You can see already that the quantities can’t be equal, because ![]() of 50 won’t yield an integer. But go ahead and see whether the answer is (A) or (B). Because
of 50 won’t yield an integer. But go ahead and see whether the answer is (A) or (B). Because ![]() of 50 is close to 6, after these dictionaries were purchased, the store would have been left with about 50 − 6 or 44 dictionaries. Then it received 10 more, giving a total of about 54 dictionaries. But this is more than the store actually ended up with; it only had 52. Therefore, it must have started with fewer than 50 dictionaries, and Quantity B is greater. (The last thing you care about is how many dictionaries it really had.)
of 50 is close to 6, after these dictionaries were purchased, the store would have been left with about 50 − 6 or 44 dictionaries. Then it received 10 more, giving a total of about 54 dictionaries. But this is more than the store actually ended up with; it only had 52. Therefore, it must have started with fewer than 50 dictionaries, and Quantity B is greater. (The last thing you care about is how many dictionaries it really had.)
6. A
There are n people in a room. One-third of them leave the room. So, there are ![]() people in the room. Four people enter the room, so you have
people in the room. Four people enter the room, so you have ![]() people. There are now
people. There are now ![]() of the original number of people in the room, therefore
of the original number of people in the room, therefore ![]() Now solve for n.
Now solve for n.
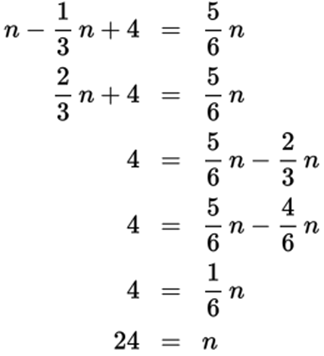
So, n = 24 and Quantity A is larger.
7. CYou may have thought this was a choice (D) question; after all, you don’t know exactly where the boards overlap, whether in the middle of each board, as pictured, or near the end of one of the boards. But that doesn’t matter; all you need to know is that they overlap and that all the angles are right angles. If the boards did not overlap, it would be easy to find the perimeter: 2 + 2 + 4 + 4 = 12 for each board, or 24 for both boards. Now, because the boards do overlap, the perimeter of the figure will be smaller than that, but how much smaller? It will be smaller by the amount of that “lost perimeter” in the middle; the perimeter of the square where the boards overlap. (You know it’s a square since all the angles are right angles.) The length of a side of that square is the shorter dimension of each of the boards: 2. Therefore, the perimeter of the square is 4 × 2 or 8. The perimeter of the figure, then, is 24 − 8 or 16. The two quantities are equal.
8. AStart by simplifying the quantity in Quantity A: ![]() is the same as
is the same as ![]() which is 4x. Subtract x from both quantities, and you’re left with 3x in Quantity A and
which is 4x. Subtract x from both quantities, and you’re left with 3x in Quantity A and ![]() in Quantity B. Now divide both sides by x, and you’re left with 3 in Quantity A and
in Quantity B. Now divide both sides by x, and you’re left with 3 in Quantity A and ![]() in Quantity B. Square both quantities, and you get 9 in Quantity A and x in Quantity B. Since x is an integer between 1 and 9, exclusive, Quantity A is larger. If the algebra seems too abstract, go ahead and use the Picking Numbers strategy. If x equals 4, then Quantity A equals (2 + 2)2 = 16, and Quantity B equals 4 + 8 = 12.
in Quantity B. Square both quantities, and you get 9 in Quantity A and x in Quantity B. Since x is an integer between 1 and 9, exclusive, Quantity A is larger. If the algebra seems too abstract, go ahead and use the Picking Numbers strategy. If x equals 4, then Quantity A equals (2 + 2)2 = 16, and Quantity B equals 4 + 8 = 12.
9. B, C, D, EIf ![]() then 3x = 2y and
then 3x = 2y and ![]() Substitute
Substitute ![]() into the equation
into the equation ![]() = 15, 2x + 3x = 30, 5x = 30, x = 6. Then,
= 15, 2x + 3x = 30, 5x = 30, x = 6. Then, ![]() and y2 = 81. So any answer with greater than 81 under the radical will be greater than y. Therefore, the correct choices are (B), (C), (D), and (E).
and y2 = 81. So any answer with greater than 81 under the radical will be greater than y. Therefore, the correct choices are (B), (C), (D), and (E).
10.A, B, EThe best place to start here is with pairs of positive integers that have a product of 10. The numbers 5 and 2 have a product of 10, as do 10 and 1. But remember that integers may be negative, so −1 and −10 are possible, as well as −2 and −5. The mean of −1 and −10 is −5.5; the mean of −2 and −5 is −3.5. The mean of 2 and 5 is 3.5. The correct answers are (A), (B), and (E).
11.C, D, EThe prime factorization of 210 is 2 × 3 × 5 × 7. The sum of the prime factors is 2 + 3 + 5 + 7 = 17. So, the correct choices are (C), (D), and (E).
12.9
Use the definition of average to write the sum of the first n bowlers’ scores: ![]() therefore, n × average = sum of scores. Substitute the values given in the question, and you have 160n = sum of scores for the initial set of bowlers. Now write the formula for the average again, using the additional score of 170. Now there are n + 1bowlers.
therefore, n × average = sum of scores. Substitute the values given in the question, and you have 160n = sum of scores for the initial set of bowlers. Now write the formula for the average again, using the additional score of 170. Now there are n + 1bowlers.
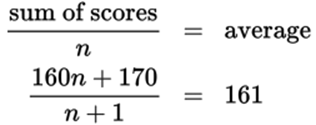
Cross multiply and use algebra to solve for n.
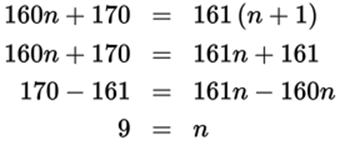
There were 9 bowlers in the original group.
13.EFirst, identify the numbers in set T: 3, 5, 7, 11, 13. The average of the numbers in set T is ![]() Its standard deviation is given in the question stem as 3.71. In order to increase the standard deviation of a set of numbers, you must add a value that is more than one standard deviation away from the mean. One standard deviation below the mean for set T would be 7.8 − 3.71 = 4.09, and one standard deviation above the mean would be 7.8 + 3.71 = 11.51. Any value outside this range 4.09 ≤ x ≤ 11.51would increase set T’s standard deviation, since it would make the set more “spread out” from the mean than it currently is. The only choice that does that is choice (E).
Its standard deviation is given in the question stem as 3.71. In order to increase the standard deviation of a set of numbers, you must add a value that is more than one standard deviation away from the mean. One standard deviation below the mean for set T would be 7.8 − 3.71 = 4.09, and one standard deviation above the mean would be 7.8 + 3.71 = 11.51. Any value outside this range 4.09 ≤ x ≤ 11.51would increase set T’s standard deviation, since it would make the set more “spread out” from the mean than it currently is. The only choice that does that is choice (E).
14.C

Solving this problem involves several steps, but none is too complicated. The circle has its center at point T. Start with the triangle on the right whose vertices are at T and two points on the circumference of the circle. This makes two of its sides radii of the circle, which we’re told each have a length of 3. Because all radii must have equal length, this makes the triangle an isosceles triangle. In addition, you’re told one of the base angles of this triangle has measure 60°. Thus, the other base angle must also have measure 60° (since the base angles in an isosceles triangle have equal measure). The sum of the two base angles is 120°, leaving 180° − 120° or 60° for the other angle, the one at point T(making ΔTUV an equilateral triangle with sides of 3).
Now, angle RTS is opposite this 60° angle, so its measure must also be 60°. Therefore, ΔRST is another equilateral triangle, and its sides are 3. Therefore, the length of RS is 3, choice (C).
15.B
The probability formula is
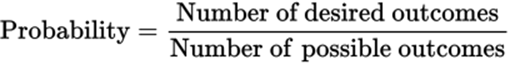
When one die is rolled, there are six possible outcomes. When two dice are rolled, the number of possible outcomes is 6 × 6, or 36. Getting a total value of 7 can be achieved in the following ways: (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), and (6, 1). There are six possible ways.
So the probability of rolling a total of 7 is ![]() which can be reduced to
which can be reduced to ![]() choice (B).
choice (B).
16.8
In the first scenario, each day, ![]() of the house will be built. Because there are 10 workers, each person can build
of the house will be built. Because there are 10 workers, each person can build ![]() of a house each day. In the second scenario, there are 15 workers, so that means
of a house each day. In the second scenario, there are 15 workers, so that means ![]() a house can be built each day. Four houses could, therefore, be built in 8 days:
a house can be built each day. Four houses could, therefore, be built in 8 days:
![]()
17.CThe residential usage (in billions) in 2000 was about 22; the usage was about 52 in 2010. The range is the difference because the residential usage increased over the time period. Therefore, 52 − 22 = 30, and the range is about 30 billion gallons. The correct answer is (C).
18.CThe two amounts were closest to each other in 2002. The residential amount appears to be about 28; the total appears to be about 32: 28 ÷ 32 = 0.875. Choice (C) is the closest.
19.DThe three usages with the greatest amounts per person are faucets, washers, and showers, totaling 30 gallons per day. Multiply by 10,000 to get 300,000, choice (D).
20.B
The residential consumption (in billions) in 2010 was approximately 52. Take half of that amount, 26, to represent the amount of water used by households with efficient appliances and plumbing. Let W represent the amount of water these households would have used otherwise.
Set up a percent equation to solve for W. Remember, the savings were 35%, so subtract 35 from 100 to find the percent that would have been used.

The savings in billions of gallons was 40 − 26 = 14. The correct answer is (B).
Diagnose Your Results
Diagnostic Tool
Tally up your score and write your results below.
Total
Total Correct: out of 20 correct
By Question Type
· Quantitative Comparison (questions 1–8) out of 8 correct
· Problem Solving (questions 9–16) out of 8 correct
· Data Interpretation (questions 17–20) out of 4 correct
Look back at the questions you got wrong and think about your experience answering them.
1. ![]() STEP 1
STEP 1
Find the roadblocks.
If you struggled to answer some questions, then to improve your score, you need to pinpoint exactly what “roadblocks” tripped you up. To do that, ask yourself the following two questions:
Am I weak in the skills being tested?
This will be very easy for you to judge. Maybe you’ve forgotten how to calculate an average or what PEMDAS stands for. If you know you need to brush up on your math skills, try the Kaplan GRE Math Workbook, which contains a focused review of all the fundamental math concepts tested on the GRE, as well as practice exercises to build speed and accuracy.
Did the question types throw me off?
Then you need to become more comfortable with them! Quantitative Comparisons have a unique format, and Data Interpretation can be daunting with its charts, graphs, and tables. If you struggled, go back to the beginning of the Quantitative Reasoning section of this book and review the Kaplan principles and methods for the question types you found challenging. Make sure you understand the principles and how to apply the methods. These strategies will help you improve your speed and efficiency on Test Day. Remember, it’s not a math test; it’s a critical reasoning test.
Also, get as much practice as you can so that you grow more at ease with the question formats. For even more practice, try the Kaplan GRE Math Workbook, which includes practice sets for each question type.
2. ![]() STEP 2
STEP 2
Find the blind spots.
Did you answer some questions quickly and confidently but get them wrong anyway?
When you come across wrong answers like these, you need to figure out what you thought you were doing right, what it turns out you were doing wrong, and why that happened. The best way to do that is to read the answer explanations!
The explanations give you a detailed breakdown of why the correct answer is correct and why all the other answers choices are incorrect. This helps to reinforce the Kaplan principles and methods for each question type and helps you figure out what blindsided you so it doesn’t happen again. Also, just as with your “roadblocks,” try to get in as much practice as you can.
3. ![]() STEP 3
STEP 3
Reinforce your strengths.
Now read through all the answer explanations for the ones you got right. You should check every explanation because, if you guessed correctly without actually knowing how to get the right answer, reading the explanations helps you make sure that you learn what you need to. Equally importantly, on a problem you knew how to do, there may be a faster way to get to the answer than the way you chose, or even just a different way. Understanding more than one approach to a given problem will deepen your critical thinking skills. Reading the explanation for a question you got right also helps to reinforce the Kaplan principles and methods for each question type, which in turn helps you work more efficiently so you can get the score you want. Keep your skills sharp with more practice.
As soon as you are comfortable with all the GRE question types and Kaplan methods, complete a full-length practice test under timed conditions. Practice tests serve as milestones; they help you to chart your progress! So don’t save them all for the final weeks before your Test Day. For even more practice, you can also try the Kaplan GRE Quiz Bank. You get more than 2,500 questions that you can access 24/7 from any Internet browser, and each question comes with a comprehensive explanation. You can even customize your quizzes based on question type, content, and difficulty level. Take quizzes in Timed Mode to test your stamina or in Tutor Mode to see explanations as you work. Best of all, you also get detailed reports to track your progress.
Visit kaptest.com/GRE for more details on our Quiz Bank and for more information on our other online and classroom-based options.
Quantitative Reasoning Practice Set 2
Numbers
All numbers are real numbers.
Figures
The position of points, lines, angles, and so on may be assumed to be in the order shown; all lengths and angle measures may be assumed to be positive.
Lines shown as straight may be assumed to be straight.
Figures lie in the plane of the paper unless otherwise stated.
Figures that accompany questions are intended to provide useful information. However, unless a note states that a figure has been drawn to scale, you should solve the problems by using your knowledge of mathematics, not by estimation or measurement.
Directions
Each of the following questions, 1–10, consists of two quantities, Quantity A and Quantity B. You are to compare the two quantities and choose
1. if Quantity A is greater
2. if Quantity B is greater
3. if the two quantities are equal
4. if the relationship cannot be determined from the information given
·
Common Information
In a question, information concerning one or both of the quantities to be compared is centered above the two quantities. A symbol that appears in both quantities represents the same thing in Quantity A as it does in Quantity B.
1.
2.
1.
1.
|
Quantity A |
Quantity B |
|
The average (arithmetic mean) of 100, 101, and 103 |
The median of 100, 101, and 103 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
2. A and B are points on the circumference of the circle with center O (not shown). The length of chord AB is 15.
|
Quantity A |
Quantity B |
|
Circumference of circle O |
12π |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
3. 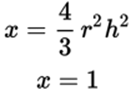
3. r and h are positive.
|
Quantity A |
Quantity B |
|
h |
|
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
4. ΔABC lies in the xy-plane with C at (0, 0), B at (6, 0), and A at (x, y), where x and y are positive. The area of ΔABC is 18 square units.
|
Quantity A |
Quantity B |
|
y |
6 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
5. For x ≠ y, ![]()
p > 0 > q
|
Quantity A |
Quantity B |
|
p Φ q |
q Φ p |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
6. x ≠ 0
|
Quantity A |
Quantity B |
|
|
|
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
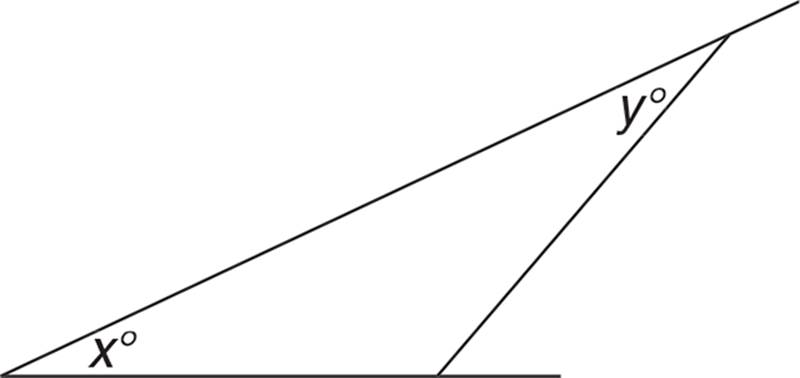
7. 
7.
|
Quantity A |
Quantity B |
|
x + y |
180° |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
8. 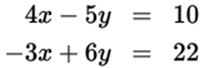
8.
|
Quantity A |
Quantity B |
|
33 |
x + y |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
9. 6(10)n > 60,006
|
Quantity A |
Quantity B |
|
n |
6 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
10.In a four-digit positive integer y, the thousands digit is 2.5 times the tens digit.
|
Quantity A |
Quantity B |
|
The tens digits of y |
4 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
3.
10.
11.What is the average (arithmetic mean) of 2x + 3, 5x − 4, 6x − 6, and 3x − 1?
1. 2x + 4
2. 3x − 2
3. 3x + 2
4. 4x − 2
5. 4x + 2
12. 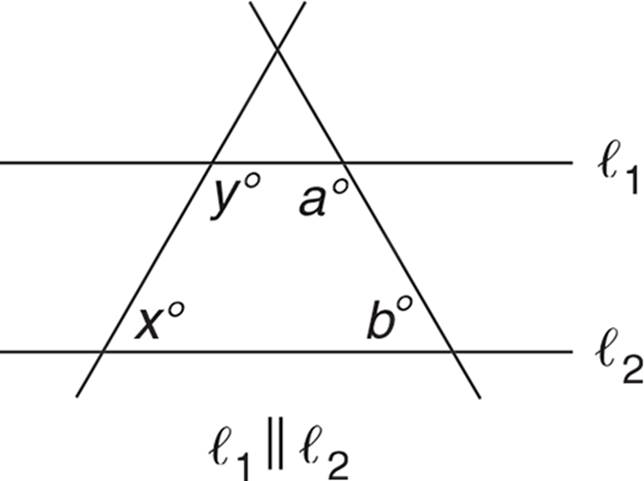
12.Which of the following statements must be true about the figure shown above?
1. x = a
2. x = b
3. a = b
4. y = b
5. x + y = a + b
13. 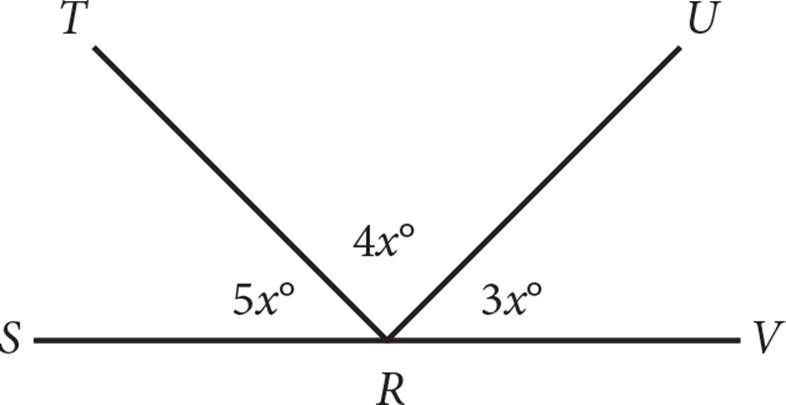
13.What is the degree measure of angle SRU?
1. 15
2. 45
3. 105
4. 135
5. 180
14.There are at least 200 apples in a grocery store. The ratio of the number of oranges to the number of apples is 9 to 10. How many oranges could there be in the store?
Indicate all possible choices.
1. 171
2. 180
3. 216
4. 252
5. 315
15. 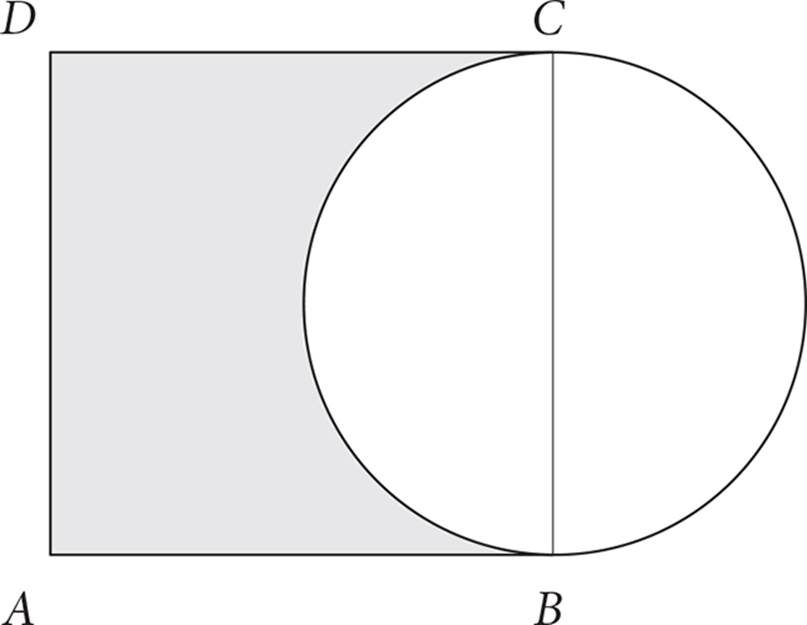
15.Square ABCD has a side length of 4. BC is the diameter of the circle. Which of the following is greater than or equal to the area of the shaded region, in square units?
Indicate all possible choices.
1. 16 − 16π
2. 16 − 4π
3. 16 − 2π
4. 16 + π
5. 16 + 4π
4. Questions 16–20 are based on the following graphs.
5. 
6.
15.
16.In 1998, what were the total profits from all hardware tool sales?
$
17.Which year had the greatest percentage increase in number of table saws sold from the previous year?
1. 1993
2. 1995
3. 1997
4. 2000
5. 2001
18.Of the following, what is the closest to the percentage change in profits from table saws between 1998 and 1999?
1. A 50% increase
2. A 33% increase
3. A 17% decrease
4. A 33% decrease
5. A 50% decrease
19.If the total manufacturing cost of table saws in 1993 was $22,000, what was the price per saw?
$
20.In 1998, what were the approximate profits from sales of cordless drills?
1. $50,000
2. $70,000
3. $80,000
4. $90,000
5. $100,000
21.
Answer Key
QUANTITATIVE REASONING PRACTICE SET 2
1. A
2. A
3. C
4. C
5. D
6. D
7. B
8. A
9. D
10.B
11.D
12.E
13.D
14.B, C, D, E
15.C, D, E
16.200,000
17.A
18.D
19.700
20.B
Answers and Explanations
QUANTITATIVE REASONING PRACTICE SET 2
1. AThis question requires no computation but only a general understanding of how averages work and what the word “median” means. The median of a group of numbers is the “middle number”; it is the value above which half of the numbers in the group fall and below which the other half fall. If you have an even number of values, the median is the average of the two “middle” numbers; if you have an odd number of values, the median is one of the values. Here, in Quantity B, the median is 101. In Quantity A, if the numbers were 100, 101, and 102, then the average would also be 101, but because the third number, 103, is greater than 102, then the average must be greater than 101. Quantity A is greater than 101, and Quantity B equals 101; Quantity A is larger.
2. AStart with the information you are given. You know that the length of the chord is 15. What does that mean? Well, because you don’t know exactly where A and B are, it doesn’t mean too much, but it does tell you that the distance between two points on the circle is 15. That tells you that the diameter must be at least 15. If the diameter were less than 15, then you couldn’t have a chord that was equal to 15, because the diameter is always the longest chord in a circle. The diameter of the circle is 15 or greater, so the circumference must be at least 15π. That means that Quantity A must be larger than Quantity B.
3. C
The equation in the centered information looks complicated, but we’ll take it one step at a time. Because Quantity A has only h in it, solve the equation for h, leaving h on one side of the equal sign and r on the other side. First, substitute the value for x into the equation; then solve for h in terms of r.
|
|
Substitute 1 for x. |
|
|
Divide both sides by |
|
|
Take the positive square root of both sides, using the information that r and h are positive. |
|
|
Divide both sides by r to get h alone. |
|
|
The two quantities are equal. |
4. C
Draw an xy-plane and label the points given to help solve this problem. You know where points B and C are; they’re on the x-axis. You don’t know where A is, however, which may make you think that the answer is choice (D). But you’re given more information: you know that the triangle has an area of 18. The area of any triangle is one-half the product of the base and the height. Make side BC the base of the triangle; you know the coordinates of both points, so you can find their distance apart, which is the length of that side. C is at the origin, the point (0, 0); B is at the point (6, 0). The distance between them is the distance from 0 to 6 along the x-axis, or just 6. So that’s the base. What about the height? Because you know that the area is 18, you can plug what you know into the area formula.
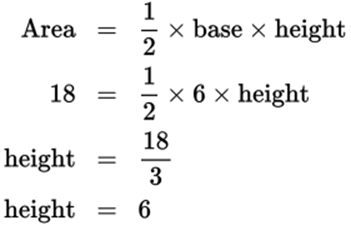
That’s the other dimension of the triangle. The height is the distance between the x-axis and point A. Now you know that A must be somewhere in the first quadrant, since both the x- and y-coordinates are positive. Don’t worry about the x-coordinate of the point, because that’s not what’s being compared; you care only about the value of y. You know that the distance from the x-axis to the point is 6, because that’s the height of the triangle, and that y must be positive. Therefore, the y-coordinate of the point must be 6. That’s what the y-coordinate is: a measure of the point’s vertical distance from the x-axis. (Note that if you hadn’t been told that y was positive, there would be two possible values for y: 6 and −6. A point that’s 6 units below the x-axis would also give a triangle with height 6.) You still don’t know the x-coordinate of the point, and in fact you can’t figure that out, but you don’t care. You know that y is 6; therefore, the two quantities are equal.
5. D
With symbolism problems like this, it sometimes helps to put the definition of the symbol into words. For this symbol, you can say something like “x Φ y means take the sum of the two numbers and divide that by the difference of the two numbers.” One good way to do this problem is to Pick Numbers. You know that p is positive and q is negative. So suppose p is 1 and q is −1. Figure out what p Φ q is first. You start by taking the sum of the numbers, or 1 + (−1) = 0. That’s the numerator of the fraction, and you don’t really need to go any further than that. Whatever their difference is, because the numerator is 0, the whole fraction must equal 0. (The difference can’t be 0 also, since p ≠ q.) So that’s p Φ q. Now what about q Φ p? Well, that’s going to have the same numerator as p Φ q: 0. The only thing that changes when you reverse the order of the numbers is the denominator of the fraction. So q Φ p has a numerator of 0, and that fraction must equal 0 as well.
So you’ve found a case where the quantities are equal. Try another set of values and see whether the quantities are always equal. If p = 1 and q = −2, then the sum of the numbers is 1 + (−2) or −1. So that’s the numerator of the fraction in each quantity. Now for the denominator of p Φ q, you need p − q = 1 − (−2) = 1 + 2 = 3. Then the value of pΦ q is ![]() The denominator of q Φ p is q − p = −2 − 1 = −3. In that case, the value of q Φ p is
The denominator of q Φ p is q − p = −2 − 1 = −3. In that case, the value of q Φ p is ![]() or
or ![]() The quantities are different; therefore, the answer is (D).
The quantities are different; therefore, the answer is (D).
6. D
Picking Numbers will help you solve this problem. For ![]() and
and ![]() so Quantity A is larger. For
so Quantity A is larger. For ![]() and
and ![]() so Quantity B is larger. The quantities are different; therefore, the answer is (D).
so Quantity B is larger. The quantities are different; therefore, the answer is (D).
7. B
The sum of the three interior angles of a triangle is 180°. Because x and y are only two of the angles, their sum must be less than 180°. Quantity B is greater.
8. A
For the system of equations 4x − 5y = 10 and −3x + 6y = 22, it is not necessary to solve for the values of x and y. Rather, you want to know about the sum of x and y. Notice what happens when you add the two equations.
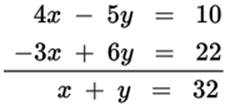
Because x + y = 32 and 33 > 32, Quantity A is larger.
9. DDivide both sides of the inequality by 6. You’re left with (10)n > 10,001. The number 10,001 can also be written as 104 + 1, so you know that (10)n > 104 + 1. Therefore, Quantity A, n, must be 5 or greater. Quantity B is 6. Because n could be less than, equal to, or greater than 6, you need more information.
10.BTry to set the quantities equal. Could the tens digit of y be 4? If it is, and the thousands digit is 2.5 times the units digit, then the tens digit must be ... 10? That can’t be right. A digit must be one of the integers 0–9; 10 isn’t a digit. Therefore, 4 is too big to be the tens digit of y. You don’t know what the tens digit of y is, but you know that it must be less than 4. Quantity B is greater than Quantity A.
11.DTo find the average, add the quantities together and divide by 4: (2x + 3) + (5x − 4) + (6x − 6) + (3x − 1) = 16x − 8 and ![]() The correct choice is (D).
The correct choice is (D).
12.E
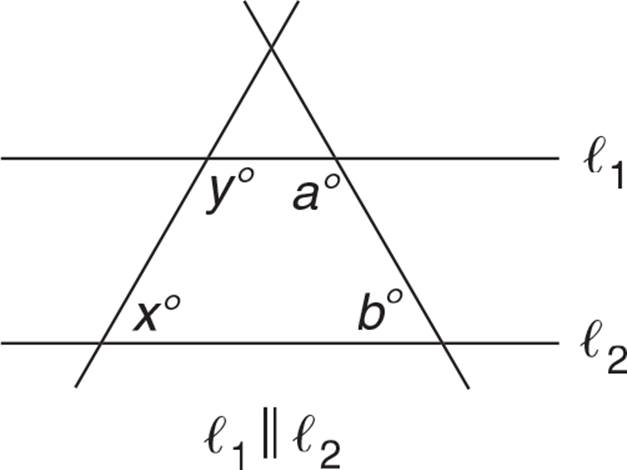
When a transversal cuts a pair of parallel lines, in this case ℓ1 and ℓ2, the angles are always supplementary and their sum is 180. So, the sum (x + y) is equal to the sum (a + b). The exact values of the individual angle measures cannot be determined from the figure. The answer is (E).
13.DFirst, find the value of x, using the fact that there are 180° in a straight line. Set the sum of the angle measures equal to 180: 5x + 4x + 3x = 180, 12x = 180, and x = 15. Angle SRU equals 4x + 5x = 9x, which is 135°. Choice (D) is correct.
14.B, C, D, EYou know that the ratio of oranges to apples is 9 to 10 and that there are at least 200 apples. The ratio tells you that there are more apples than oranges. At the minimum, there must be 180 oranges to satisfy the proportion ![]() There could be more than 200 apples, so any number of oranges greater than 180 for which the ratio 9:10 applies is also correct. All of the choices are multiples of 9, so the correct choices are (B), (C), (D), and (E).
There could be more than 200 apples, so any number of oranges greater than 180 for which the ratio 9:10 applies is also correct. All of the choices are multiples of 9, so the correct choices are (B), (C), (D), and (E).
15.C, D, E
The area of the shaded region is the area of the square minus the area of the portion of the circle that is inside the square. The area of a square is its side squared. The area of square ABCD is 42 = 4 × 4, which is 16. Now find the area of the portion of the circle that is inside the square. Because the diameter of the circle is a side of the square, you know that exactly one-half of the circle’s area is inside the square. Also, because the diameter of the circle is twice the radius, the radius of the circle is ![]() or 2. The area of a circle with a radius r is πr2. The area of the complete circle in this question is π(22), which is 4π. So half the area of this circle is 2π. Thus, the area of the shaded region is 16 − 2π.
or 2. The area of a circle with a radius r is πr2. The area of the complete circle in this question is π(22), which is 4π. So half the area of this circle is 2π. Thus, the area of the shaded region is 16 − 2π.
That means that 16 − 4π and 16 − 16π are less than 16 − 2π, so they cannot be correct choices. However, the sum of 16 and any positive number is greater than 16 and also greater than 16 − 2π. So, the correct choices are (C), (D), and (E).
16.200,000
From the second bar graph, the profits from table saws in 1998 were $60,000. From the pie chart, table saws were 30% of the total profits. Let’s call the total profits T dollars. Then 30% of T dollars is $60,000. So 0.3T = 60,000, and
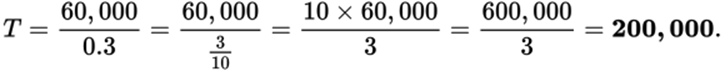
17.AUse the first bar graph to analyze number of table saws sold. The year with the biggest percent increase over the previous year will be the year in which the increase is the biggest fraction of the amount from the previous year. Notice that in 1993, the increase from 1992 was approximately 60 - 30, or 30. This is approximately a 100% increase, and it is the greatest percent increase over the previous year among all the years from 1993 to 2001. There was a greater increase in number of table saws from 1996 to 1997 than from 1992 to 1993, about 110 − 70 = 40. However, the percent increase from 1996 to 1997 is approximately ![]() which is less than 100%, so choice (A) is correct.
which is less than 100%, so choice (A) is correct.
18.D
In 1998, the profits from table saws were approximately $60,000. In 1999, the profits from table saws were approximately $40,000. From 1998 to 1999, there was a decrease in the profits from table saws. In general,
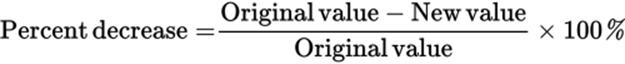
Here, the percent decrease is approximately
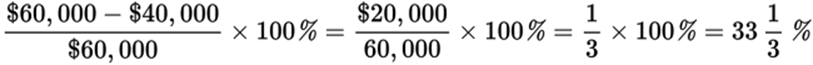
A percent decrease of ![]() is closest to (D).
is closest to (D).
19.700In 1993, the profits were $20,000. Using the formula Profit = Revenue − Cost, you can write Revenue = Cost + Profit. The cost was $22,000. So the revenue was $22,000 + $20,000 = $42,000. Because in 1993, 60 table saws were sold, each table saw was sold for ![]() which is $700.
which is $700.
20.B
In 1998, the profits from table saws were about $60,000, and this profit was 30% of the total profits. Let’s call the total profits T dollars. Then 30% of T dollars is $60,000. So 0.3T= 60,000, and
![]()
The total profits in 1998 were approximately $200,000 (you may also have remembered this calculation from question 16). The profits from cordless drills were 35% of the total. So the profits from cordless drills were approximately 0.35($200,000), which is $70,000 or answer choice (B).
Diagnose Your Results
Diagnostic Tool
Tally up your score and write your results below.
Total
Total Correct: out of 20 correct
By Question Type
· Quantitative Comparison (questions 1–10) out of 10 correct
· Problem Solving (questions 11–15) out of 5 correct
· Data Interpretation (questions 16–20) out of 5 correct
Repeat the steps outlined in the Diagnose Your Results page that follows the Quantitative Reasoning Practice Set 1 answer key.
Quantitative Reasoning Practice Set 3
Numbers
All numbers are real numbers.
Figures
The position of points, lines, angles, and so on may be assumed to be in the order shown; all lengths and angle measures may be assumed to be positive.
Lines shown as straight may be assumed to be straight.
Figures lie in the plane of the paper unless otherwise stated.
Figures that accompany questions are intended to provide useful information. However, unless a note states that a figure has been drawn to scale, you should solve the problems by using your knowledge of mathematics, not by estimation or measurement.
Directions
1. if Quantity A is greater
2. if Quantity B is greater
3. if the two quantities are equal
4. if the relationship cannot be determined from the information given
Each of the following questions, 1–8, consists of two quantities, Quantity A and Quantity B. You are to compare the two quantities and choose
·
Common Information
In a question, information concerning one or both of the quantities to be compared is centered above the two quantities. A symbol that appears in both quantities represents the same thing in Quantity A as it does in Quantity B.
1.
2.
1.
1. The diameter of a circle equals the diagonal of a square whose side length is 4.
|
Quantity A |
Quantity B |
|
The circumference of the circle |
|
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
2. 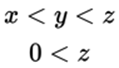
2.
|
Quantity A |
Quantity B |
|
x |
0 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
3.
|
Quantity A |
Quantity B |
|
The number of distinct positive integer factors of 96 |
The number of distinct positive integer factors of 72 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
4. x > 0
|
Quantity A |
Quantity B |
|
|
|
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
5. 2p = 4q
|
Quantity A |
Quantity B |
|
p |
2q |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
6.
|
Quantity A |
Quantity B |
|
The number of seconds in 7 hours |
The number of hours in 52 weeks |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
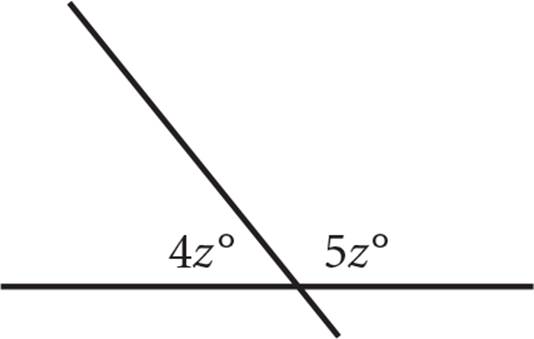
7. 
7.
|
Quantity A |
Quantity B |
|
z |
20 |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
8. x > 2
|
Quantity A |
Quantity B |
|
x3 |
4x |
1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.
3.
8.
9. If ![]() and
and ![]() what is the value of
what is the value of ![]()
10.Rectangle A has a length of 12 inches and a width of 5 inches. Rectangle B has a length of 9 inches and a width of 10 inches. By what number must the area of rectangle A be multiplied in order to get the area of rectangle B?
11. 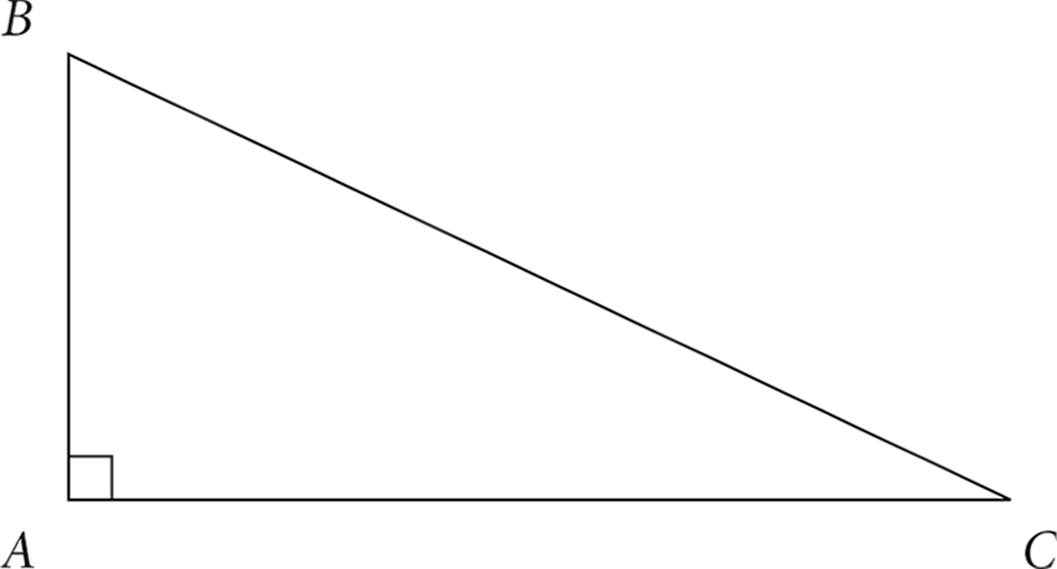
11.In right triangle ABC above, side AB has a length of 5 units, while side BC has a length of 13 units. What is the area of ABC, in square units?
square units
12.If the average test score of four students is 85, which of the following scores could a fifth student receive such that the average of all five scores is greater than 84 and less than 86?
Indicate all such scores.
1. 88
2. 86
3. 85
4. 83
5. 80
13.Meg is twice as old as Rolf, but three years ago, she was two years older than Rolf is now. How old is Rolf now?
years old
14.The cost, in cents, of manufacturing x crayons is 570 + 0.5x. The crayons sell for 10 cents each. What is the minimum number of crayons that need to be sold so that the revenue received recoups the manufacturing cost?
1. 50
2. 57
3. 60
4. 61
5. 95
15.If xy ≠ 0, ![]()
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
4. Questions 16–20 refer to the following graphs:
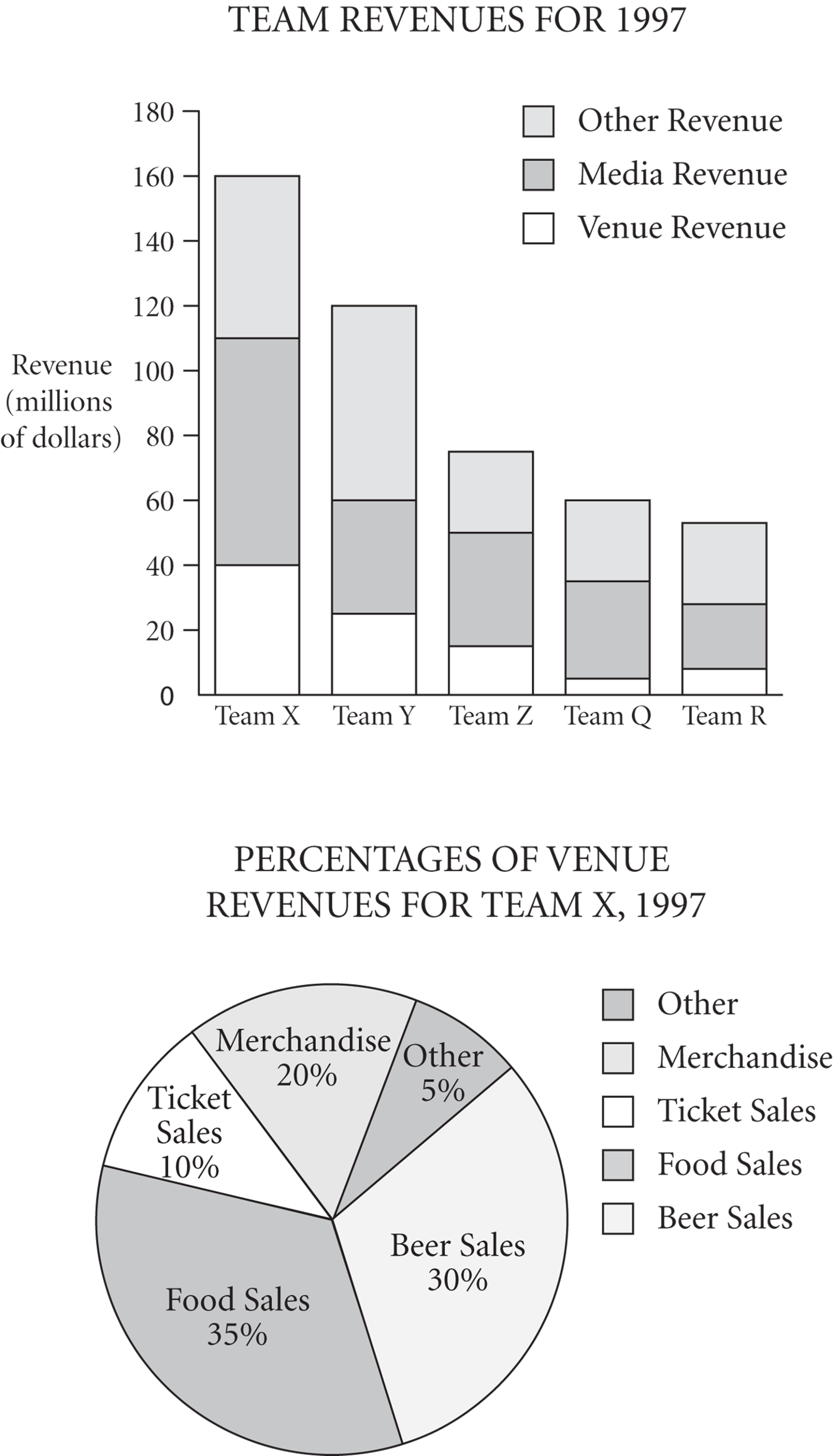
5. 
6.
15.
16.For the team with the median venue revenue in 1997, media revenue represented approximately what percent of that team’s total revenue?
1. 25%
2. 30%
3. 45%
4. 70%
5. 85%
17.Of the following, which is greater than the amount of revenue, in millions of dollars, earned by Team X through food sales in 1997?
Indicate all such amounts.
1. 7
2. 10
3. 14
4. 18
5. 22
18.In 1997, which teams had media revenues of less than $25 million?
Indicate all such teams.
1. Team X
2. Team Y
3. Team Z
4. Team Q
5. Team R
19.If Team Y earned total revenues of at least $150 million in 1998, then Team Y’s total revenue could have increased by what percent from 1997 to 1998?
Indicate all such percents.
1. 20%
2. 25%
3. 30%
4. 35%
5. 40%
20.The venue revenues for Team X from merchandise sales and ticket sales were approximately what percent of the venue revenues for Team X from food sales?
1. 43%
2. 53%
3. 67%
4. 71%
5. 86%
Answer Key
QUANTITATIVE REASONING PRACTICE SET 3
1. B
2. D
3. C
4. A
5. C
6. A
7. C
8. A
9. 5
10.1.5
11.30
12.A, B, C, D
13.5
14.C
15.A
16.C
17.D, E
18.E
19.B, C, D, E
20.E
Answers and Explanations
QUANTITATIVE REASONING PRACTICE SET 3
1. BThe diagonal of a square of side 4 is ![]() The circumference of a circle is π times the diameter. So, the circumference of this circle is
The circumference of a circle is π times the diameter. So, the circumference of this circle is ![]() Now write Quantity B,
Now write Quantity B, ![]() as
as![]() and you can compare the quantities piece by piece. The factors of 4 and
and you can compare the quantities piece by piece. The factors of 4 and ![]() are the same in both quantities, but π is less than 5. So, Quantity B is larger.
are the same in both quantities, but π is less than 5. So, Quantity B is larger.
2. DYou could Pick Numbers here or else just use logic. You know that z is positive and that x and y are less than z. But does that mean that x or y must be negative? Not at all—they could be, but they could also be positive. For instance, suppose x = 1, y = 2, and z = 3. Then Quantity A would be larger. However, if x = -1, y = 0, and z = 1, then Quantity B would be larger. You need more information to determine the relationship between the quantities. The answer is (D).
3. CThere are 12 positive integer factors of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96. There are 12 positive integer factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72. The two quantities are equal.
4. AIf x > 0, then ![]() which also equals
which also equals ![]() must be greater than 1. On the other hand,
must be greater than 1. On the other hand, ![]() must be less than 1. This is because when x > 0, the numerator x is smaller than the denominator, so the ratio
must be less than 1. This is because when x > 0, the numerator x is smaller than the denominator, so the ratio ![]() Therefore,
Therefore, ![]() when x > 0, and Quantity A is greater.
when x > 0, and Quantity A is greater.
5. C
For this question, notice the relationship between the bases, 2 and 4. When comparing exponents, it’s easiest to work with equal bases.
You know that 4 = 22. Therefore, 4q = (22)q = 22q. Now you have 2p = 22q, so p = 2q. The quantities are equal, choice (C).
6. A
Before you go to the trouble of multiplying the terms, let’s see if there’s a shortcut. For the GRE, make sure you know the common unit conversions for time. There are 60 seconds in a minute and 60 minutes in an hour, so there are 7 × 60 × 60 seconds in 7 hours. There are 24 hours in a day and 7 days in a week, so there are 7 × 24 × 52 hours in 52 weeks. Let’s rewrite the quantities:
|
Quantity A |
Quantity B |
|
7 × 60 × 60 |
7 × 24 × 52 |
Taking away the common values gives you:
|
Quantity A |
Quantity B |
|
60 × 60 |
24 × 52 |
You still shouldn’t do the math, however. The best strategy is to compare piece by piece, which shows that Quantity A is larger than Quantity B.
7. CThe sum of the measures of the angles on one side of a straight line is 180°. Therefore, 4z + 5z = 180, so 9z = 180. Divide both sides by 9 to find z = 20. (C) is the answer.
8. ASince x > 2, you know x > 0 and you can divide both quantities by x without changing their relationship. Quantity A is then x2 and Quantity B is 4. Since x > 2, the least value for x2is greater than 22 = 4. Therefore, (A) is correct.
9. 5
Let’s first find the value of ![]() Then we’ll find the value of
Then we’ll find the value of ![]()
o Since ![]()
o Therefore, ![]()
o Since ![]()
![]()
o Therefore, ![]()
10.1.5
The area of a rectangle is its length times its width.
The area of rectangle A is 12 × 5 = 60.
The area of rectangle B is 9 × 10 = 90.
So the area 60 of rectangle A must be multiplied by a number, which you can call x, to obtain the area 90 of rectangle B.
Then 60x = 90. So ![]()
11.30
Here's a problem where it really pays to have learned the special right triangles. Because one leg of the right triangle is 5 and the hypotenuse is 13, you have a special right triangle, the 5:12:13 right triangle. So the length of AC is 12.
The area of a triangle is ![]() of the base times the height. The area of a right triangle is
of the base times the height. The area of a right triangle is ![]() because one leg can be considered to be the base and the other leg can be considered to be the height. So the area of triangle ABC is
because one leg can be considered to be the base and the other leg can be considered to be the height. So the area of triangle ABC is
![]()
The answer is 30.
12.A, B, C, D
The average formula is as follows:
![]()
Therefore,
Sum of the terms = Average × Number of terms
The sum of the scores of the four students whose average was 85 is 85(4) = 340. Let’s call the fifth student’s score x. If the new average is to be greater than 84 and less than 86 and the sum of the scores of all five students is 340 + x, then ![]() If you multiply all parts of the inequality by 5, you get 420 < 340 + x < 430. Subtracting 340 from all parts of the inequality, you get 80 < x < 90, making (A), (B), (C), and (D) the correct choices.
If you multiply all parts of the inequality by 5, you get 420 < 340 + x < 430. Subtracting 340 from all parts of the inequality, you get 80 < x < 90, making (A), (B), (C), and (D) the correct choices.
13.5
This question can be broken into two equations with two unknowns, Meg’s age now (M) and Rolf ’s age now (R). Equation (i) shows the relationship now; equation (ii) shows the relationship three years ago.
(i) M = 2 × R (ii) M − 3 = R + 2
Substitute 2R for M in equation (ii) and solve for R:
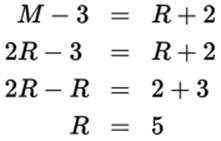
Rolf is 5 years old now.
14.C
The cost of manufacturing x crayons is (570 + 0.5x) cents. Because each crayon sells for 10 cents, x crayons will sell for 10x cents. You want the smallest value of x such that 10xcents is at least 570 + 0.5x cents. So you must solve the equation 10x = 570 + 0.5x for the value of x that will recoup the investment.
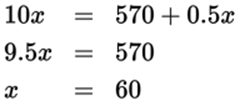
The minimum number of crayons is 60, choice (C).
Alternatively, you could have avoided setting up an algebraic equation by Backsolving, starting with either (B) or (D).
15.A
You can write that ![]() Canceling a factor of x from the numerator and denominator of
Canceling a factor of x from the numerator and denominator of ![]() you have
you have ![]()
So, ![]() The answer is (A).
The answer is (A).
16.C
Before you answer any graph question, begin by examining the graphs. Here you have two graphs, a segmented bar graph representing team revenue breakdowns for five teams and a pie chart showing the distribution of venue revenues for Team X.
You’re now ready to attack the question, which asks you to find the team with the median venue revenue for 1997 and to determine what percent of that team’s total revenue is media revenue. This question must refer to the first graph, and the first part of the question—finding the team with the median venue revenue—is straightforward. Median refers to the number in the middle. Looking at the white portions of the bars in the top graph, you see that Team Z has the median venue revenue. The fastest approach to the answer here (and throughout graph questions generally) is to approximate. The downside to bar graphs is that it’s often very hard to get a read on the values. The upside is that if you approximate, often you don’t have to read the values. Here you need to determine what percent of Team Z’s bar is represented by media revenue (the segment in the middle—always be especially careful to isolate the correct piece of data). By approximating, you can see that the middle segment is about half of the entire bar. Thus the correct answer has to be close to 50%. The only answer choice that works is (C), 45%.
17.D, EThe key to this question is that it involves both graphs. The question asks for the amount Team X earned through food sales, which takes you first to the pie chart, where you see that food sales accounted for 35% of the venue revenues for Team X. But to convert that to a dollar amount, you need a figure for the amount earned in venue revenues by Team X in 1997. According to the bar graph, this is $40 million. Now, take 35% of $40 million: 0.35 × 40 = 14, so the answer is any amount greater than 14. The answers are (D) and (E).
18.ELook at the bar graph: Team Q had media revenues of 35 − 5 = 30 million, and Teams X, Y, and Z had media revenues greater than those of team Q. Team R had media revenue of 30 − 10 = 20 million. The only correct choice is (E).
19.B, C, D, E
Percent change problems are extremely popular graph questions, and as long as you set them up correctly, they are a great opportunity. This question asks for the approximate percent increase in Team Y’s total revenue from 1997 to 1998, so you need to figure out (roughly) the amount of increase, place that over the original (or smaller) amount, and then convert the fraction into a percent. You are given the total revenue for 1998 as at least $150 million, so you need to locate the total revenue for 1997 from the bar graph. It looks to be approximately $120 million, so the amount of increase is $30 million (or more), and the original amount is $120 million. Now let’s apply the formula:
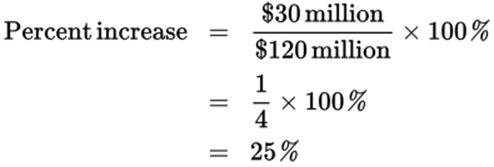
So, any percent greater than or equal to 25% is the answer. The answers are (B), (C), (D), and (E).
20.E
Looking at the bar graph, you see from the lowest portion of the bar for Team X that venue revenues of Team X were approximately 40 million dollars (call it 40m, for short). From the pie chart, the venue revenues of Team X from merchandise sales were approximately 20% of 40 million dollars, the venue revenues from ticket sales were approximately 10%, and the venue revenues from food sales were approximately 35%. The venue revenues of Team X from merchandise, in dollars, were approximately 0.2(40m) = 8m. The venue revenues of Team X from ticket sales, in dollars, were approximately 0.1(40m) = 4m. So the venue revenues of Team X from merchandise sales and ticket sales, in dollars, were approximately 8m + 4m = 12m. The venue revenues of Team X from food sales, in dollars, were approximately 0.35(40m) = 14m. The percent that the venue revenues of Team X that were from merchandise sales and ticket sales, out of the venue revenues of Team X that were from food sales, is approximately
![]()
To the nearest percent, 85.7% is 86%. Choice (E) is correct.
Diagnose Your Results
Diagnostic Tool
Tally up your score and write your results below.
Total
Total Correct: out of 20 correct
By Question Type
· Quantitative Comparison (questions 1–8) out of 8 correct
· Problem Solving (questions 9–15) out of 7 correct
· Data Interpretation (questions 16–20) out of 5 correct
Repeat the steps outlined in the Diagnose Your Results page that follows the Quantitative Reasoning Practice Set 1 answer key.