Cracking the AP Chemistry Exam

Part IV

Content Review for the AP Chemistry Exam

Chapter 6

Big Idea #4: Chemical Reactions and their Rates

RATE LAW USING CONCENTRATION AND TIME

It’s also useful to have rate laws that relate the rate constant k to the way that concentrations change over time. The rate laws will be different depending on whether the reaction is first, second, or zero order, but each rate law can be expressed as a graph that relates the rate constant, the concentration of a reactant, and the elapsed time.

First-Order Rate Laws

The rate of a first-order reaction depends on the concentration of a single reactant raised to the first power.

Rate = k[A]

As the concentration of reactant A is depleted over time, the rate of reaction will decrease with a characteristic half-life. The half-life of a reaction describes the amount of time it takes for half of a sample to react. For the first order reaction graphed below, the half-life of A is 1 minute. In the first minute, the concentration of A drops by half, from 1.0 M to 0.5 M. In the second minute, it drops from 0.5 M to 0.25 M, and so forth. A concentration versus time graph for a first-order reactant will always display the typical half-life exponential decay curve as shown below.

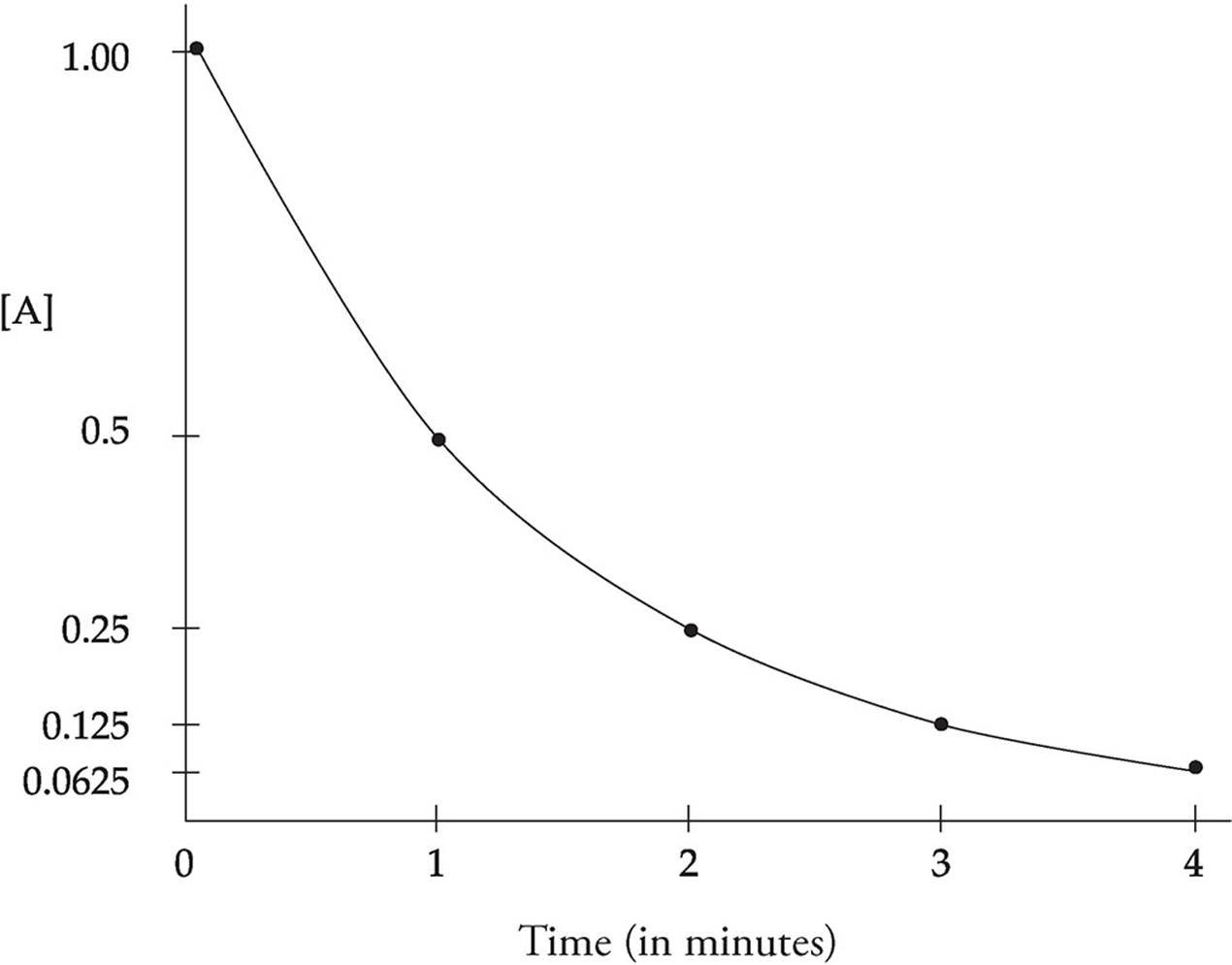
The rate law for a first-order reaction uses natural logarithms.

The use of natural logarithms in the rate law creates a linear graph comparing concentration and time. The slope of the line is given by −k and the y-intercept is given by ln[A]₀.

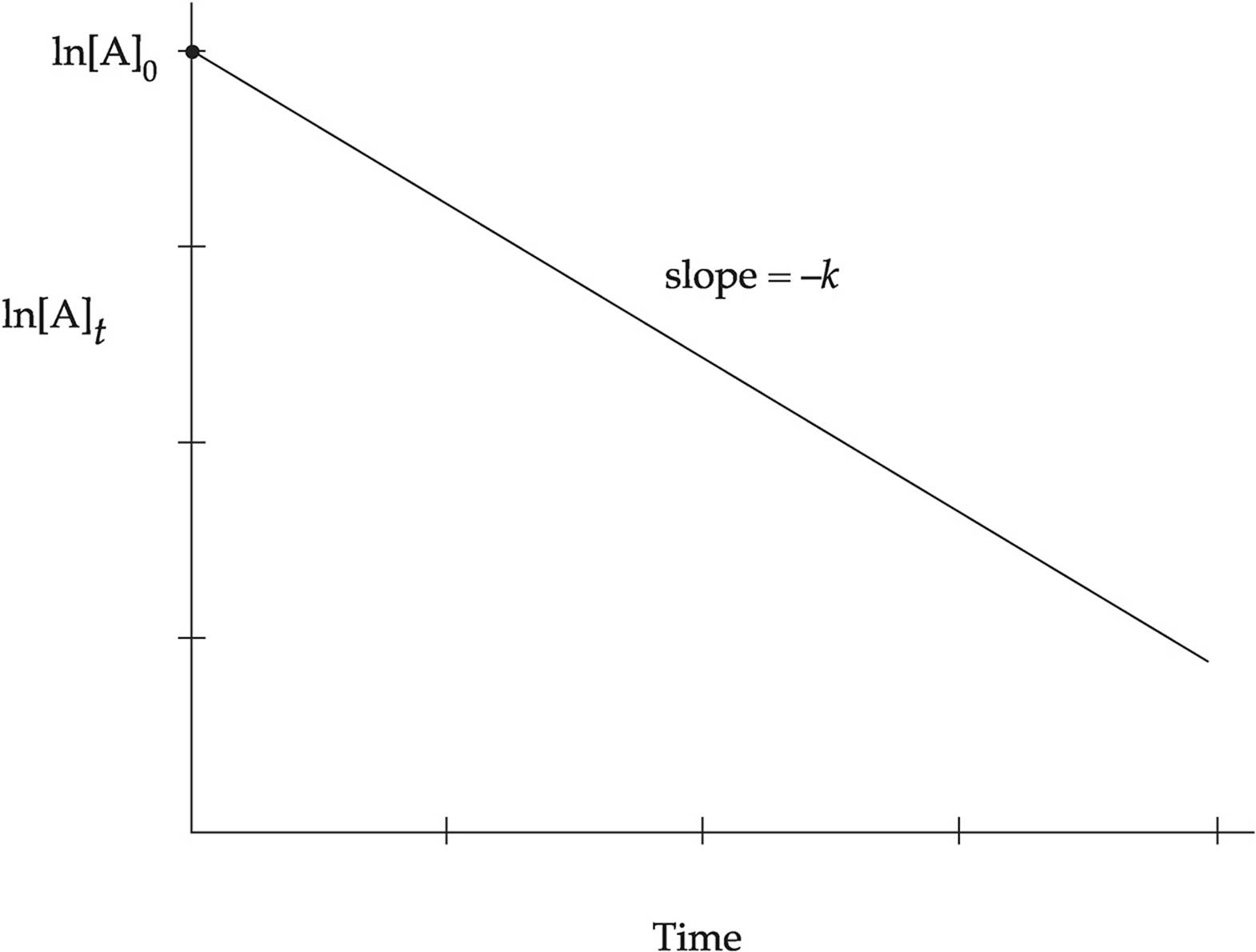
Using slope intercept form, we can interpret this graph to come up with a useful equation.

y = mx + b

y = ln[A]_t

m = −k

x = time

b = ln [A]₀

After substitution and rearrangement, the slope intercept equation becomes:

First-Order Rate Law

ln[A]_t = −kt + ln[A]₀

[A]_t = concentration of reactant A at time t

[A]₀ = initial concentration of reactant A

 k = rate constant

 t = time elapsed

Half-Life

The half-life of a reactant in a chemical reaction is the time it takes for half of the substance to react. Most half-life-problems can be solved by using a simple chart:

Reminder

Don’t forget that the
chart should start with
the time at zero.

So a sample with a mass of 120 grams and a half-life of 3 years will decay as follows:

Additionally, the half-life of a first order reactant can be calculated from the graphical interpretation of the reaction using the following formula:

Half-life =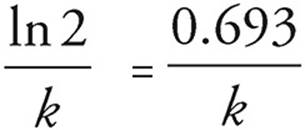

Let’s try an example based on the data below.

(a) Let’s find the value of k. We’ll use the first two lines of the table.

ln[A]_t − ln[A]₀ = −kt

ln(1.6) − ln(2.0) = −k(5 min)

−0.22 = −(5 min)k

k = 0.045 min⁻¹

(b) Now let’s use k to find [A] when 20 minutes have elapsed.

ln[A]_t − ln[A]₀ = −kt

ln[A]_t − ln(2.0) = −(0.045 min⁻¹)(20 min)

ln[A]_t = −0.21

[A]_t = e^−0.21 = 0.81 M

(c) Now let’s find the half-life of the reaction.

We can look at the answer (b) to see that the concentration dropped by half (1.6 M to 0.8 M) from 5 minutes to 20 minutes. That makes the half-life about 15 minutes. We can confirm this using the half-life equation.

Half-life = 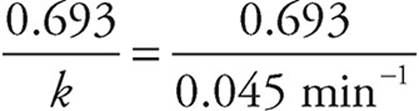= 15.4 minutes

Another use of half-life is to examine the rate of decay of a radioactive substance. A radioactive substance is one that will slowly decay into a more stable form as time goes on.

Second-Order Rate Laws

The rate of a second-order reaction depends on the concentration of a single reactant raised to the second power.

Rate = k[A]²

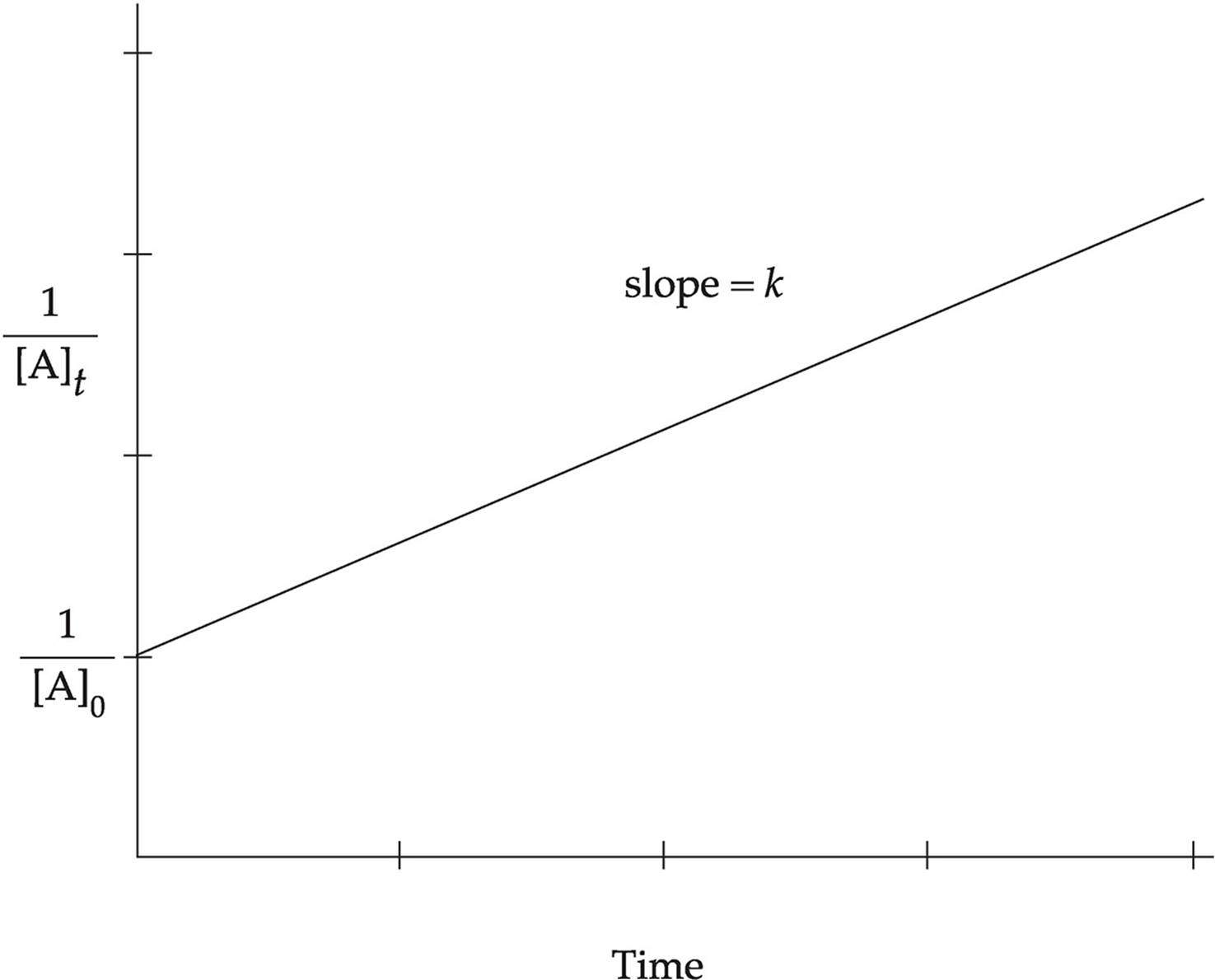
The rate law for a second-order reaction uses the inverses of the concentrations.

Second-Order Rate Law

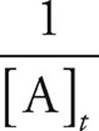= kt +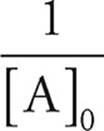

[A]_t = concentration of reactant A at time t

[A]₀ = initial concentration of reactant A

k = rate constant

t = time elapsed

The use of inverses in the rate law creates a linear graph comparing concentration and time. Notice that the line moves upward as the concentration decreases. The slope of the line is given by k and the y-intercept is given by .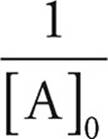

Zero-Order Rate Laws

The rate of a zero-order reaction does not depend on the concentration of reactants at all, so the rate of a zero-order reaction will always be the same at a given temperature.

Rate = k

The graph of the change in concentration of a reactant of a zero-order reaction versus time will be a straight line with a slope equal to −k.