CHEMISTRY THE CENTRAL SCIENCE
11 LIQUIDS AND INTERMOLECULAR FORCES
11.4 PHASE CHANGES
Liquid water left uncovered in a glass eventually evaporates. An ice cube left in a warm room quickly melts. Solid CO2 (sold as a product called dry ice) sublimes at room temperature; that is, it changes directly from solid to gas. In general, each state of matter—solid, liquid, gas—can transform into either of the other two states. ![]() FIGURE 11.20 shows the names associated with these transformations, which are called either phase changes or changes of state.
FIGURE 11.20 shows the names associated with these transformations, which are called either phase changes or changes of state.
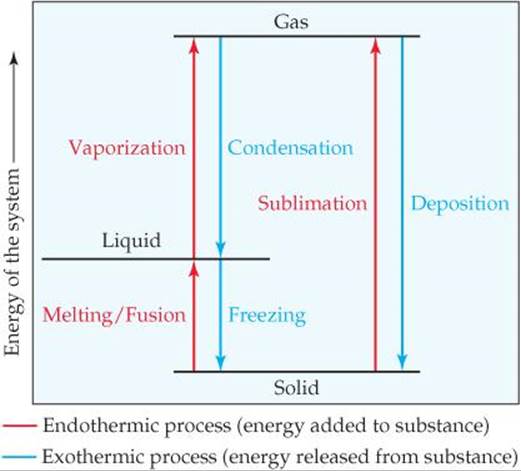
![]() FIGURE 11.20 Phase changes and the names associated with them.
FIGURE 11.20 Phase changes and the names associated with them.
Energy Changes Accompanying Phase Changes
Every phase change is accompanied by a change in the energy of the system. In a solid, for example, the particles—either molecules, ions, or atoms—are in more or less fixed positions with respect to one another and closely arranged to minimize the energy of the system. As the temperature of the solid increases, the particles vibrate about their equilibrium positions with increasingly energetic motion. When the solid melts, the particles are freed to move relative to one another, which ordinarily means the average distance between particles increases.
Melting is called (somewhat confusingly) fusion. The increased freedom of motion of the particles comes at a price, measured by the heat of fusion or enthalpy of fusion, ΔHfus. The heat of fusion of ice, for example, is 6.01 kJ/mol.
As the temperature of the liquid increases, the particles move about with increasing energy. One measure of this increasing energy is that the concentration of gas-phase particles above the liquid surface increases with temperature. These gas-phase particles exert a pressure called vapor pressure. We explore vapor pressure in Section 11.5. For now we just need to understand that vapor pressure increases with increasing temperature until it equals the external pressure above the liquid, typically atmospheric pressure. At this point the liquid boils—the particles move into the gaseous state where they are widely separated. The energy required to cause this transition is called either the heat of vaporization or the enthalpy of vaporization, ΔHvap. For water, the heat of vaporization is 40.7 kJ/mol.
![]() FIGURE 11.21 shows ΔHfus and ΔHvap values for four substances. The values of ΔHvap tend to be larger than the values of ΔHfus because in the transition from liquid to gas, particles must essentially sever all their interparticle attractive interactions, whereas in the transition from solid to liquid, many of these attractive interactions remain operative.
FIGURE 11.21 shows ΔHfus and ΔHvap values for four substances. The values of ΔHvap tend to be larger than the values of ΔHfus because in the transition from liquid to gas, particles must essentially sever all their interparticle attractive interactions, whereas in the transition from solid to liquid, many of these attractive interactions remain operative.
The particles of a solid can move directly into the gaseous state. The enthalpy change required for this transition is called the heat of sublimation, denoted ΔHsub. As illustrated in Figure 11.21, ΔHsub is the sum of ΔHfus and ΔHvap. Thus, ΔHsub for water is approximately 47 kJ/mol.
![]() GO FIGURE
GO FIGURE
Is it possible to calculate the heat of sublimation for a substance given its heats of vaporization and fusion? If so, what is the relationship?
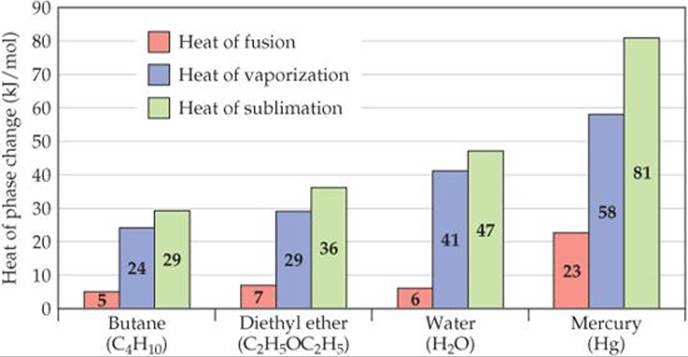
![]() FIGURE 11.21 Heats of fusion, vaporization, and sublimation.
FIGURE 11.21 Heats of fusion, vaporization, and sublimation.
Phase changes show up in important ways in our everyday experiences. When we use ice cubes to cool a drink, for instance, the heat of fusion of the ice cools the liquid. We feel cool when we step out of a swimming pool or a warm shower because the liquid water's heat of vaporization is drawn from our bodies as the water evaporates from our skin. Our bodies use this mechanism to regulate body temperature, especially when we exercise vigorously in warm weather. A refrigerator also relies on the cooling effects of vaporization. Its mechanism contains an enclosed gas that can be liquefied under pressure. The liquid absorbs heat as it subsequently evaporates, thereby cooling the interior of the refrigerator.
What happens to the heat absorbed when the liquid refrigerant vaporizes? According to the first law of thermodynamics ![]() (Section 5.2), this absorbed heat must be released when the gas condenses to liquid. As this phase change occurs, the heat released is dissipated through cooling coils in the back of the refrigerator. Just as for a given substance the heat of condensation is equal in magnitude to the heat of vaporization and has the opposite sign, so also the heat of deposition for a given substance is exothermic to the same degree that the heat of sublimation is endothermic; the heat of freezing is exothermic to the same degree that the heat of fusion is endothermic (see Figure 11.20).
(Section 5.2), this absorbed heat must be released when the gas condenses to liquid. As this phase change occurs, the heat released is dissipated through cooling coils in the back of the refrigerator. Just as for a given substance the heat of condensation is equal in magnitude to the heat of vaporization and has the opposite sign, so also the heat of deposition for a given substance is exothermic to the same degree that the heat of sublimation is endothermic; the heat of freezing is exothermic to the same degree that the heat of fusion is endothermic (see Figure 11.20).
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
What is the name of the phase change that occurs when ice left at room temperature changes to liquid water? Is this change exothermic or endothermic?
Heating Curves
When we heat an ice cube initially at –25 °C and 1 atm pressure, the temperature of the ice increases. As long as the temperature is below 0 °C, the ice cube remains in the solid state. When the temperature reaches 0 °C, the ice begins to melt. Because melting is an endothermic process, the heat we add at 0 °C is used to convert ice to liquid water, and the temperature remains constant until all the ice has melted. Once all the ice has melted, adding more heat causes the temperature of the liquid water to increase.
A graph of temperature versus amount of heat added is called a heating curve. ![]() FIGURE 11.22 shows the heating curve for transforming ice, H2O(s), initially at –25 °C to steam, H2O(g), at 125 °C. Heating the H2O(s) from –25 °C to 0 °C is represented by the line segment AB, and converting the H2O(s) at 0 °C to H2O(ℓ) at 0 °C is the horizontal segment BC. Additional heat increases the temperature of the H2O(ℓ) until the temperature reaches 100 °C (segment CD). The heat is then used to convert H2O(ℓ) to H2O(g) at a constant temperature of 100 °C (segment DE). Once all the H2O(ℓ) has been converted to H2O(g), the H2O(g) is heated to its final temperature of 125 °C (segment EF).
FIGURE 11.22 shows the heating curve for transforming ice, H2O(s), initially at –25 °C to steam, H2O(g), at 125 °C. Heating the H2O(s) from –25 °C to 0 °C is represented by the line segment AB, and converting the H2O(s) at 0 °C to H2O(ℓ) at 0 °C is the horizontal segment BC. Additional heat increases the temperature of the H2O(ℓ) until the temperature reaches 100 °C (segment CD). The heat is then used to convert H2O(ℓ) to H2O(g) at a constant temperature of 100 °C (segment DE). Once all the H2O(ℓ) has been converted to H2O(g), the H2O(g) is heated to its final temperature of 125 °C (segment EF).
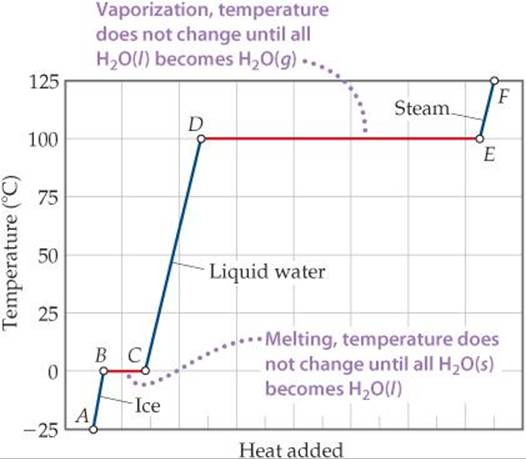
![]() FIGURE 11.22 Heating curve for water. Changes that occur when 1.00 mol of H2O is heated from H2O(s) at –25 °C to H2O(g) at 125 °C at a constant pressure of 1 atm. Heat is added over the entire temperature range, but the temperature of the system increases only when the H2O is either all solid or all liquid or all gas (blue lines). Even though heat is being added continuously, the system temperature does not change during the two phase changes (red lines).
FIGURE 11.22 Heating curve for water. Changes that occur when 1.00 mol of H2O is heated from H2O(s) at –25 °C to H2O(g) at 125 °C at a constant pressure of 1 atm. Heat is added over the entire temperature range, but the temperature of the system increases only when the H2O is either all solid or all liquid or all gas (blue lines). Even though heat is being added continuously, the system temperature does not change during the two phase changes (red lines).
We can calculate the enthalpy change of the system for each segment of the heating curve. In segments AB, CD, and EF we are heating a single phase from one temperature to another. As we saw in Section 5.5, the amount of heat needed to raise the temperature of a substance is given by the product of the specific heat, mass, and temperature change (Equation 5.22). The greater the specific heat of a substance, the more heat we must add to accomplish a certain temperature increase. Because the specific heat of water is greater than that of ice, the slope of segment CD is less than that of segment AB. This lesser slope means the amount of heat we must add to a given mass of liquid water to achieve a 1 °C temperature change is greater than the amount we must add to achieve a 1 °C temperature change in the same mass of ice.
In segments BC and DE we are converting one phase to another at a constant temperature. The temperature remains constant during these phase changes because the added energy is used to overcome the attractive forces between molecules rather than to increase their average kinetic energy. For segment BC, the enthalpy change can be calculated by using ΔHfus, and for segment DE we can use ΔHvap.
SAMPLE EXERCISE 11.3 Calculating ΔH for Temperature and Phase Changes
Calculate the enthalpy change upon converting 1.00 mol of ice at –25 °C to steam at 125 °C under a constant pressure of 1 atm. The specific heats of ice, liquid water, and steam are and 2.03 J/g-K, 4.18 J/g-K, and 1.84 J/g-K, respectively. For H2O, and ΔHfus = 6.01 kJ/mol and ΔHvap = 40.67 kJ/mol.
SOLUTION
Analyze Our goal is to calculate the total heat required to convert 1 mol of ice at –25 °C to steam at 125 °C.
Plan We can calculate the enthalpy change for each segment and then sum them to get the total enthalpy change (Hess's law, Section 5.6).
Solve: For segment AB in Figure 11.22, we are adding enough heat to ice to increase its temperature by 25 °C. A temperature change of 25 °C is the same as a temperature change of 25 K, so we can use the specific heat of ice to calculate the enthalpy change during this process:
AB: ΔH = (1.00 mol)(18.0 g/mol)(2.03 J/g-K)(25 K) = 914 J = 0.91 kJ
For segment BC in Figure 11.22, in which we convert ice to water at 0 °C, we can use the molar enthalpy of fusion directly:
BC: ΔH = (1.00 mol)(6.01 kJ/mol) = 6.01 kJ
The enthalpy changes for segments CD, DE, and EF can be calculated in similar fashion:
CD: ΔH = (1.00 mol)(18.0 g/mol)(4.18 J/g-K)(100 K) = 7520 J = 7.52 kJ
DE: ΔH = (1.00 mol)(40.67 kJ/mol) = 40.7 kJ
EF: ΔH = (1.00 mol)(18.0 g/mol)(1.84 J/g-K)(25 K) = 830 J = 0.83 kJ
The total enthalpy change is the sum of the changes of the individual steps:
ΔH = 0.91 kJ + 6.01 kJ + 7.52 kJ + 40.7 kJ + 0.83 kJ = 56.0 kJ
Check The components of the total energy change are reasonable relative to the horizontal lengths (heat added) of the segments in Figure 11.22. Notice that the largest component is the heat of vaporization.
PRACTICE EXERCISE
What is the enthalpy change during the process in which 100.0 g of water at 50.0 °C is cooled to ice at –30.0 °C? (Use the specific heats and enthalpies for phase changes given in Sample Exercise 11.3.)
Answer: –20.9 kJ –33.4 kJ –6.09 kJ = –60.4 kJ
If we start with 1 mole of steam at 125 °C and cool it, we move right to left across Figure 11.22. We first lower the temperature of the H2O(g)(F → E), then condense it (E → D) to H2O(ℓ), and so forth.
Sometimes as we remove heat from a liquid, we can temporarily cool it below its freezing point without forming a solid. This phenomenon, called supercooling, occurs when the heat is removed so rapidly that the molecules have no time to assume the ordered structure of a solid. A supercooled liquid is unstable; particles of dust entering the solution or gentle stirring is often sufficient to cause the substance to solidify quickly.
Critical Temperature and Pressure
A gas normally liquefies at some point when pressure is applied. Suppose we have a cylinder fitted with a piston, and the cylinder contains water vapor at 100 °C. If we increase the pressure on the water vapor, liquid water will form when the pressure is 760 torr. However, if the temperature is 110 °C, the liquid phase does not form until the pressure is 1075 torr. At 374 °C the liquid phase forms only at 1.655 × 105 torr (217.7 atm). Above this temperature no amount of pressure causes a distinct liquid phase to form. Instead, as pressure increases, the gas becomes steadily more compressed. The highest temperature at which a distinct liquid phase can form is called the critical temperature. The critical pressure is the pressure required to bring about liquefaction at this critical temperature.
TABLE 11.5 • Critical Temperatures and Pressures of Selected Substances
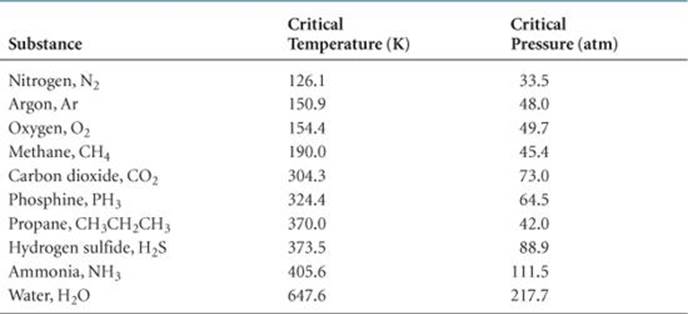
The critical temperature is the highest temperature at which a liquid can exist. Above the critical temperature, the kinetic energies of the molecules are greater than the attractive forces that lead to the liquid state regardless of how much the substance is compressed to bring the molecules closer together. The greater the intermolecular forces, the higher the critical temperature of a substance.
Several critical temperatures and pressures are listed in ![]() TABLE 11.5. Notice that nonpolar, low-molecular-weight substances, which have weak intermolecular attractions, have lower critical temperatures and pressures than substances that are polar or of higher molecular weight. Notice also that water and ammonia have exceptionally high critical temperatures and pressures as a consequence of strong intermolecular hydrogen-bonding forces.
TABLE 11.5. Notice that nonpolar, low-molecular-weight substances, which have weak intermolecular attractions, have lower critical temperatures and pressures than substances that are polar or of higher molecular weight. Notice also that water and ammonia have exceptionally high critical temperatures and pressures as a consequence of strong intermolecular hydrogen-bonding forces.
Because they provide information about the conditions under which gases liquefy, critical temperatures and pressures are often of considerable importance to engineers and other people working with gases. Sometimes we want to liquefy a gas; other times we want to avoid liquefying it. It is useless to try to liquefy a gas by applying pressure if the gas is above its critical temperature. For example, O2 has a critical temperature of 154.4 K. It must be cooled below this temperature before it can be liquefied by pressure. In contrast, ammonia has a critical temperature of 405.6 K. Thus, it can be liquefied at room temperature (approximately 295 K) by applying sufficient pressure.
When the temperature exceeds the critical temperature and the pressure exceeds the critical pressure, the liquid and gas phases are indistinguishable from each other, and the substance is in a state called a supercritical fluid. Like liquids, supercritical fluids can behave as solvents dissolving a wide range of substances. Using supercritical fluid extraction, the components of mixtures can be separated from one another. Supercritical fluid extraction has been successfully used to separate complex mixtures in the chemical, food, pharmaceutical, and energy industries. Supercritical CO2 is a popular choice because it is relatively inexpensive and there are no problems associated with disposing of solvent, nor are there toxic residues resulting from the process.