CHEMISTRY THE CENTRAL SCIENCE
14 CHEMICAL KINETICS
14.2 REACTION RATES
The speed of an event is defined as the change that occurs in a given time interval, which means that whenever we talk about speed, we necessarily bring in the notion of time. For example, the speed of a car is expressed as the change in the car's position over a certain time interval. The units of this speed are usually miles per hour—that is, the quantity that is changing (position measured in miles) divided by a time interval (measured in hours).
Similarly, the speed of a chemical reaction—its reaction rate—is the change in the concentration of reactants or products per unit of time. The units for reaction rate are usually molarity per second (M/s)—that is, the change in concentration measured in molarity divided by a time interval measured in seconds.
Let's consider the hypothetical reaction A → B, depicted in 
FIGURE 14.3. Each red sphere represents 0.01 mol of A, each blue sphere represents 0.01 mol of B, and the container has a volume of 1.00 L. At the beginning of the reaction, there is 1.00 mol A, so the concentration is 1.00 mol/L = 1.00 M. After 20 s the concentration of A has fallen to 0.54 M and the concentration of B has risen to 0.46 M. The sum of the concentrations is still 1.00 M because 1 mol of B is produced for each mole of A that reacts. After 40 s the concentration of A is 0.30 M and that of B is 0.70 M.
GO FIGURE
If A converts completely to B, what type of molecules will the container hold?
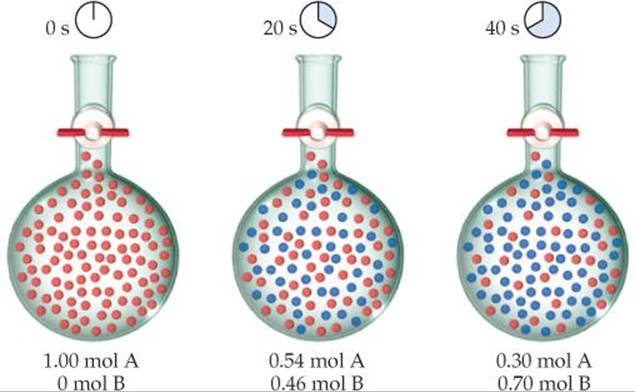
FIGURE 14.3 Progress of a hypothetical reaction A → B.
The rate of this reaction can be expressed either as the rate of disappearance of re-actant A or as the rate of appearance of product B. The average rate of appearance of B over a particular time interval is given by the change in concentration of B divided by the change in time:
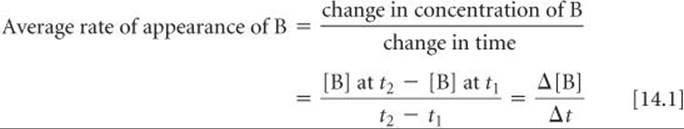
We use brackets around a chemical formula, as in [B], to indicate molarity. The Greek letter delta, Δ, is read “change in” and is always equal to a final value minus an initial value. 
(Section 5.2) The average rate of appearance of B over the 20-s interval from the beginning of the reaction (t1 = 0 s to t2 = 20 s) is
We could equally well express the reaction rate in term of the reactant, A. In this case we would be describing the rate of disappearance of A, which we express as
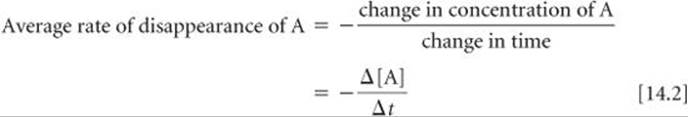
Notice the minus sign in this equation, which we use to indicate that the concentration of A decreases. By convention, rates are always expressed as positive quantities. Because [A] decreases, Δ[A] is a negative number. The minus sign we put in the equation converts the negative Δ[A] to a positive rate of disappearance.
Because one molecule of A is consumed for every molecule of B that forms, the average rate of disappearance of A equals the average rate of appearance of B:
SAMPLE EXERCISE 14.1 Calculating an Average Rate of Reaction
From the data in Figure 14.3, calculate the average rate at which A disappears over the time interval from 20 s to 40 s.
SOLUTION
Analyze We are given the concentration of A at 20 s (0.54 M) and at 40 s (0.30 M) and asked to calculate the average rate of reaction over this time interval.
Plan The average rate is given by the change in concentration, Δ[A], divided by the change in time, Δt. Because A is a reactant, a minus sign is used in the calculation to make the rate a positive quantity.
PRACTICE EXERCISE
Use the data in Figure 14.3 to calculate the average rate of appearance of B over the time interval from 0 s to 40 s.
Answer: 1.8 × 10–2M/s
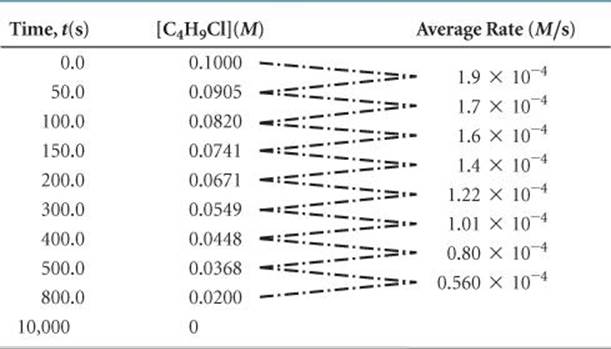
TABLE 14.1 • Rate Data for Reaction of C4H9Cl with Water
Change of Rate with Time
Now let's consider the reaction between butyl chloride (C4H9Cl) and water to form butyl alcohol (C4H9OH) and hydrochloric acid:
Suppose we prepare a 0.1000-M aqueous solution of C4H9Cl and then measure the concentration of C4H9Cl at various times after time zero (which is the instant at which the reactants are mixed, thereby initiating the reaction). We can use the resulting data, shown in the first two columns of 
TABLE 14.1, to calculate the average rate of disappearance of C4H9Cl over various time intervals; these rates are given in the third column. Notice that the average rate decreases over each 50-s interval for the first several measurements and continues to decrease over even larger intervals through the remaining measurements. It is typical for rates to decrease as a reaction proceeds because the concentration of reactants decreases. The change in rate as the reaction proceeds is also seen in a graph of [C4H9Cl] versus time (
FIGURE 14.4). Notice how the steepness of the curve decreases with time, indicating a decreasing reaction rate.
GO FIGURE
How does the instantaneous rate of reaction change as the reaction proceeds?
FIGURE 14.4 Concentration of butyl chloride (C4H9Cl) as a function of time.
Instantaneous Rate
Graphs showing how the concentration of a reactant or product changes with time, such as Figure 14.4, allow us to evaluate the instantaneous rate of a reaction, which is the rate at a particular instant during the reaction. The instantaneous rate is determined from the slope of the curve at a particular point in time. We have drawn two tangent lines in Figure 14.4, a dashed line running through the point at t = 0 s and a solid line running through the point at t = 600 s. The slopes of these tangent lines give the instantaneous rates at these two time points.* To determine the instantaneous rate at 600 s, we construct horizontal and vertical lines to form the blue right triangle in Figure 14.4. The slope of the tangent line is the ratio of the height of the vertical side to the length of the horizontal side:
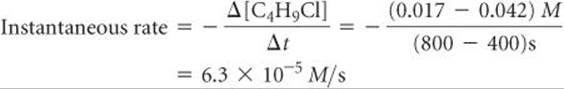
In discussions that follow, the term rate means instantaneous rate unless indicated otherwise. The instantaneous rate at t = 0 is called the initial rate of the reaction. To understand the difference between average and instantaneous rates, imagine you have just driven 98 mi in 2.0 hr. Your average speed for the trip is 49 mi/hr, but your instantaneous speed at any moment during the trip is the speedometer reading at that moment.
SAMPLE EXERCISE 14.2 Calculating an Instantaneous Rate of Reaction
Using Figure 14.4, calculate the instantaneous rate of disappearance of C4H9Cl at t = 0 s (the initial rate).
SOLUTION
Analyze We are asked to determine an instantaneous rate from a graph of reactant concentration versus time.
Plan To obtain the instantaneous rate at t = 0 s, we must determine the slope of the curve at t = 0. The tangent is drawn on the graph as the hypotenuse of the tan triangle. The slope of this straight line equals the change in the vertical axis divided by the corresponding change in the horizontal axis (that is, change in molarity over change in time).
Solve The tangent line falls from [C4H9Cl] = 0.100 M to 0.060 M in the time change from 0 s to 210 s. Thus, the initial rate is
PRACTICE EXERCISE
Using Figure 14.4, determine the instantaneous rate of disappearance of C4H9Cl at t = 300 s.
Answer: 1.1 × 10–4M/s
GIVE IT SOME THOUGHT
What is the difference between average rate and instantaneous rate? In a given reaction, can these two rates ever have the same numeric value?
Reaction Rates and Stoichiometry
During our discussion of the hypothetical reaction A → B, we saw that the stoichiometry requires that the rate of disappearance of A equal the rate of appearance of B. Likewise, the stoichiometry of Equation 14.3 indicates that 1 mol of C4H9OH is produced for each mole of C4H9Cl consumed. Therefore, the rate of appearance of C4H9OH equals the rate of disappearance of C4H9Cl:
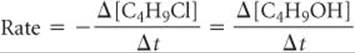
What happens when the stoichiometric relationships are not one-to-one? For example, consider the reaction 2 HI(g) → H2(g) + I2(g). We can measure either the rate of disappearance of HI or the rate of appearance of either H2 or I2. Because 2 mol of HI disappear for each mole of H2 or I2 that forms, the rate of disappearance of HI is twice the rate of appearance of either H2 or I2. How do we decide which number to use for the rate of the reaction? Depending on whether we monitor HI, I2, or H2, the rates can differ by a factor of two. To fix this problem, we need to take into account the reaction stoichiometry. To arrive at a number for the reaction rate that does not depend on which component we measured, we must divide the rate of disappearance of HI by 2 (its coefficient in the balanced chemical equation):
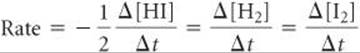
In general, for the reaction
the rate is given by
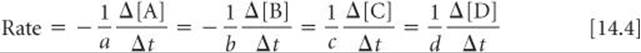
When we speak of the rate of a reaction without specifying a particular reactant or product, we mean the rate in this sense.*
SAMPLE EXERCISE 14.3 Relating Rates at Which Products Appear and Reactants Disappear
(a) How is the rate at which ozone disappears related to the rate at which oxygen appears in the reaction 2 O3(g) → 3 O2(g)?
(b) If the rate at which O2 appears, Δ[O2]/Δt, is 6.0 × 10–5M/s at a particular instant, at what rate is O3 disappearing at this same time, –Δ[O3]/Δt?
SOLUTION
Analyze We are given a balanced chemical equation and asked to relate the rate of appearance of the product to the rate of disappearance of the reactant.
Plan We can use the coefficients in the chemical equation as shown in Equation 14.4 to express the relative rates of reactions.
Solve
(a) Using the coefficients in the balanced equation and the relationship given by Equation 14.4, we have:
(b) Solving the equation from part (a) for the rate at which O3 disappears, –Δ[O3]/Δt, we have:
Check We can apply a stoichiometric factor to convert the O2 formation rate to the O3 disappearance rate:
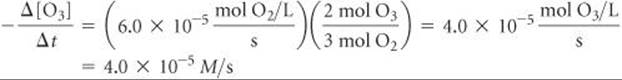
PRACTICE EXERCISE
If the rate of decomposition of N2O5 in the reaction 2 N2O5(g) → 4 NO2(g) + O2(g) at a particular instant is 4.2 × 10–7M/s, what is the rate of appearance of (a) NO2 and (b) O2 at that instant?
Answers: (a) 8.4 × 10–7M/s, (b) 2.1 × 10–7M/s