CHEMISTRY THE CENTRAL SCIENCE
16 ACID–BASE EQUILIBRIA
16.4 THE pH SCALE
The molar concentration of H+(aq) in an aqueous solution is usually very small. For convenience, we therefore usually express [H+] in terms of pH, which is the negative logarithm in base 10 of [H+]:*
If you need to review the use of logarithms, see Appendix A.
We can use Equation 16.17 to calculate the pH of a neutral solution at 25°C (that is, one in which [H+] = 1.0 × 10–7M):
pH = –log(1.0 × 10–7) = –(–7.00) = 7.00
The pH of a neutral solution is 7.00 at 25 °C. Notice that the pH is reported with two decimal places. We do so because only the numbers to the right of the decimal point are the significant figures in a logarithm. Because our original value for the concentration (1.0 × 10–7M) has two significant figures, the corresponding pH has two decimal places (7.00).
TABLE 16.1 • Relationships among (H+), (OH–), and pH at 25 °C
What happens to the pH of a solution as we make the solution more and more acidic, so that [H+] increases? Because of the negative sign in the logarithm term of Equation 16.17, the pH decreases as [H+] increases. For example, the pH of a neutral solution ([H+] = 1.0 × 10–7M) is 7.00, but when we add sufficient acid to make [H+] = 1.0 × 10–3M the pH is
At 25°C the pH of an acidic solution is less than 7.00.
We can also calculate the pH of a basic solution, one in which [OH–] > 1.0 × 10–7M. Suppose [OH–] = 2.0 × 10–3M. We can use Equation 16.16 to calculate [H+] for this solution and Equation 16.17 to calculate the pH:
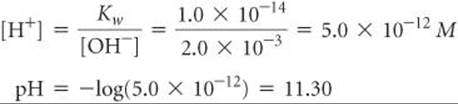
At 25 °C the pH of a basic solution is greater than 7.00. The relationships among [H+], [OH–], and pH are summarized in 
TABLE 16.1.
GIVE IT SOME THOUGHT
Is it possible for a solution to have a negative pH? If so, would that pH signify a basic or acidic solution?
You might think that when [H+] is very small, as is often the case, it would be unimportant. Nothing is further from the truth. If [H+] is part of a kinetic rate law, for example, changing its concentration changes the rate. 
(Section 14.3) Thus, if the rate law is first order in [H+], doubling the H+ concentration doubles the rate even if the change is merely from 1 × 10–7M to 2 × 10–7M. In biological systems, many reactions involve proton transfers and have rates that depend on [H+]. Because the speeds of these reactions are crucial, the pH of biological fluids must be maintained within narrow limits. For example, human blood has a normal pH range of 7.35 to 7.45. Illness and even death can result if the pH varies much from this narrow range.
SAMPLE EXERCISE 16.6 Calculating pH from [H+]
Calculate the pH values for the two solutions of Sample Exercise 16.5.
SOLUTION
Analyze We are asked to determine the pH of aqueous solutions for which we have already calculated [H+].
Plan We can calculate pH using its defining equation, Equation 16.17.
Solve
(a) In the first instance we found [H+] to be 1.0 × 10–12M, so that
Because 1.0 × 10–12 has two significant figures, the pH has two decimal places, 12.00.
(b) For the second solution, [H+] = 5.6 × 10–6M. Before performing the calculation, it is helpful to estimate the pH. To do so, we note that [H+] lies between 1 × 10–6 and 1 × 10–5. Thus, we expect the pH to lie between 6.0 and 5.0. We use Equation 16.17 to calculate the pH:
Check After calculating a pH, it is useful to compare it to your estimate. In this case the pH, as we predicted, falls between 6 and 5. Had the calculated pH and the estimate not agreed, we should have reconsidered our calculation or estimate or both.
PRACTICE EXERCISE
(a) In a sample of lemon juice, [H+] = 3.8 × 10–4M. What is the pH? (b) A commonly available window-cleaning solution has [OH–] = 1.9 × 10–6M. What is the pH?
Answers: (a) 3.42, (b) [H+] = 5.3 × 10–9M, so pH = 8.28
pOH and Other “p” Scales
The negative logarithm is a convenient way of expressing the magnitudes of other small quantities. We use the convention that the negative logarithm of a quantity is labeled “p” (quantity). Thus, we can express the concentration of OH– as pOH:
Likewise, pKw equals –log Kw.
By taking the negative logarithm of both sides of the equilibrium-constant expression for water, Kw = [H+][OH–], we obtain
from which we obtain the useful expression
The pH and pOH values characteristic of a number of familiar solutions are shown in 
FIGURE 16.5. Notice that a change in [H+] by a factor of 10 causes the pH to change by 1. Thus, the concentration of H+(aq) in a solution of pH 6 is 10 times the H+(aq) concentration in a solution of pH 7.
GIVE IT SOME THOUGHT
If the pOH for a solution is 3.00, what is the pH? Is the solution acidic or basic?
SAMPLE EXERCISE 16.7 Calculating [H+] from pOH
A sample of freshly pressed apple juice has a pOH of 10.24. Calculate [H+].
SOLUTION
Analyze We need to calculate [H+] from pOH.
Plan We will first use Equation 16.20, pH + pOH = 14.00, to calculate pH from pOH. Then we will use Equation 16.17 to determine the concentration of H+.
Solve From Equation 16.20, we have
Next we use Equation 16.17:
Thus,
To find [H+], we need to determine the antilogarithm of –3.76. Scientific calculators have an an-tilogarithm function (sometimes labeled INV log or 10x) that allows us to perform the calculation:
Comment The number of significant figures in [H+] is two because the number of decimal places in the pH is two.
Check Because the pH is between 3.0 and 4.0, we know that [H+] will be between 1.0 × 10–3M and 1.0 × 10–4M. Our calculated [H+] falls within this estimated range.
PRACTICE EXERCISE
A solution formed by dissolving an antacid tablet has a pH of 9.18. Calculate [OH–].
Answer: [OH–] = 1.5 × 10–5
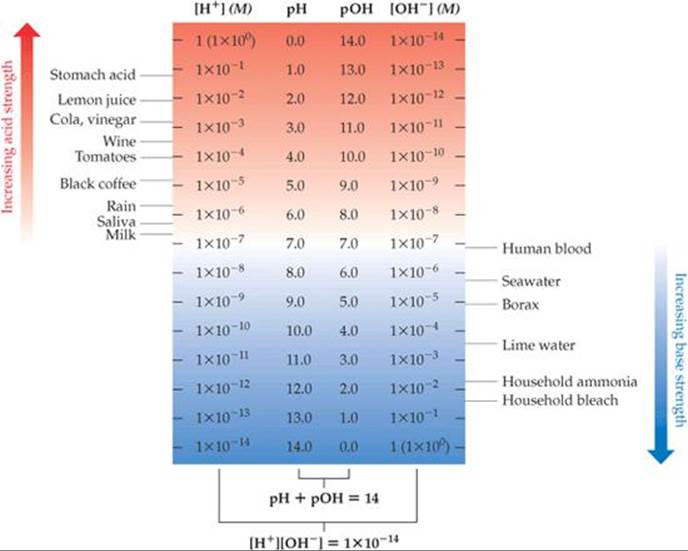
FIGURE 16.5 Concentrations of H+ and pH values of some common substances at 25 °C.
Measuring pH
The pH of a solution can be measured with a pH meter (FIGURE 16.6). A complete understanding of how this important device works requires a knowledge of electrochemistry, a subject we take up in Chapter 20. In brief, a pH meter consists of a pair of electrodes connected to a meter capable of measuring small voltages, on the order of millivolts. A voltage, which varies with pH, is generated when the electrodes are placed in a solution. This voltage is read by the meter, which is calibrated to give pH.
FIGURE 16.6 A digital pH meter. The device is a millivoltmeter, and the electrodes immersed in a solution produce a voltage that depends on the pH of the solution.
Although less precise, acid–base indicators can be used to measure pH. An acid–base indicator is a colored substance that can exist in either an acid or a base form. The two forms have different colors. Thus, the indicator has one color at lower pH and another at higher pH. If you know the pH at which the indicator turns from one form to the other, you can determine whether a solution has a higher or lower pH than this value. Litmus, for example, changes color in the vicinity of pH 7. The color change, however, is not very sharp. Red litmus indicates a pH of about 5 or lower, and blue litmus indicates a pH of about 8 or higher.
GO FIGURE
If a colorless solution turns pink when we add phenolphthalein, what can we conclude about the pH of the solution?
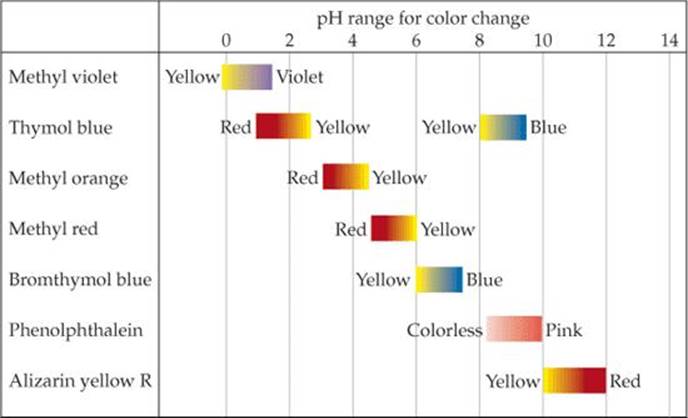
FIGURE 16.7 pH ranges for common acid–base indicators. Most indicators have a useful range of about 2 pH units.
Some common indicators are listed in FIGURE 16.7. The chart tells us, for instance, that methyl red changes color over the pH interval from about 4.5 to 6.0. Below pH 4.5 it is in the acid form, which is red. In the interval between 4.5 and 6.0, it is gradually converted to its basic form, which is yellow. Once the pH rises above 6 the conversion is complete, and the solution is yellow. This color change, along with that of the indicators bromthymol blue and phenolphthalein, is shown in 
FIGURE 16.8. Paper tape impregnated with several indicators is widely used for determining approximate pH values.
GO FIGURE
Which of these indicators is best suited to distinguish between a solution that is slightly acidic and one that is slightly basic?
FIGURE 16.8 Solutions containing three common acid–base indicators at various pH values.