CHEMISTRY THE CENTRAL SCIENCE
19 CHEMICAL THERMODYNAMICS
19.5 GIBBS FREE ENERGY
We have seen examples of endothermic processes that are spontaneous, such as the dissolution of ammonium nitrate in water. 
(Section 13.1) We learned in our discussion of the solution process that a spontaneous process that is endothermic must be accompanied by an increase in the entropy of the system. However, we have also encountered processes that are spontaneous and yet proceed with a decrease in the entropy of the system, such as the highly exothermic formation of sodium chloride from its constituent elements. (Section 8.2) Spontaneous processes that result in a decrease in the system's entropy are always exothermic. Thus, the spontaneity of a reaction seems to involve two thermodynamic concepts, enthalpy and entropy.
How can we use ΔH and ΔS to predict whether a given reaction occurring at constant temperature and pressure will be spontaneous? The means for doing so was first developed by the American mathematician J. Willard Gibbs (1839–1903). Gibbs (
FIGURE 19.15)proposed a new state function, now called the Gibbs free energy (or just free energy), G, and defined as
where T is the absolute temperature. For an isothermal process, the change in the free energy of the system, ΔG, is
Under standard conditions, this equation becomes
To see how the state function G relates to reaction spontaneity, recall that for a reaction occurring at constant temperature and pressure
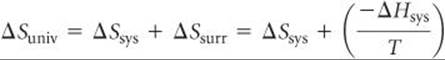
where we have used Equation 19.9 to substitute for ΔSsurr. Multiplying both sides by –T gives us
GO FIGURE
Are the processes that move a system toward equilibrium spontaneous or nonspontaneous?
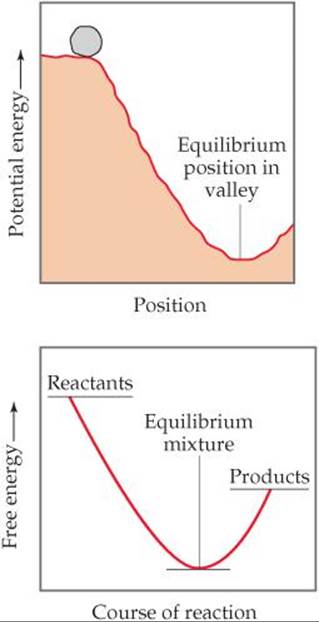
FIGURE 19.16 Potential energy and free energy. An analogy is shown between the gravitational potential-energy change of a boulder rolling down a hill and the free-energy change in a spontaneous reaction.
Comparing Equations 19.11 and 19.13, we see that in a process occurring at constant temperature and pressure, the free-energy change, ΔG, is equal to –TΔSuniv. We know that for spontaneous processes, ΔSuniv is always positive and, therefore, –TΔSuniv is always negative. Thus, the sign of ΔG provides us with extremely valuable information about the spontaneity of processes that occur at constant temperature and pressure. If both T and P are constant, the relationship between the sign of ΔG and the spontaneity of a reaction is as follows:
1. If ΔG < 0, the reaction is spontaneous in the forward direction.
2. If ΔG = 0, the reaction is at equilibrium.
3. If ΔG > 0, the reaction in the forward direction is nonspontaneous (work must be done to make it occur) but the reverse reaction is spontaneous.
It is more convenient to use ΔG as a criterion for spontaneity than to use ΔSuniv because ΔG relates to the system alone and avoids the complication of having to examine the surroundings.
An analogy is often drawn between the free-energy change during a spontaneous reaction and the potential-energy change when a boulder rolls down a hill (
FIGURE 19.16). Potential energy in a gravitational field “drives” the boulder until it reaches a state of minimum potential energy in the valley. Similarly, the free energy of a chemical system decreases until it reaches a minimum value. When this minimum is reached, a state of equilibrium exists. In any spontaneous process carried out at constant temperature and pressure, the free energy always decreases.
To illustrate these ideas, let's return to the Haber process for the synthesis of ammonia from nitrogen and hydrogen, which we discussed extensively in Chapter 15:
Imagine that we have a reaction vessel that allows us to maintain a constant temperature and pressure and that we have a catalyst that allows the reaction to proceed at a reasonable rate. What happens when we charge the vessel with a certain number of moles of N2 and three times that number of moles of H2? As we saw in Figure 15.3, the N2 and H2 react spontaneously to form NH3 until equilibrium is achieved. Similarly, Figure 15.3 shows that if we charge the vessel with pure NH3, it decomposes spontaneously to N2 and H2 until equilibrium is reached. In each case the free energy of the system gets progressively lower and lower as the reaction moves toward equilibrium, which represents a minimum in the free energy. We illustrate these cases in FIGURE 19.17.
GO FIGURE
Why are the spontaneous processes shown sometimes said to be “downhill” in free energy?
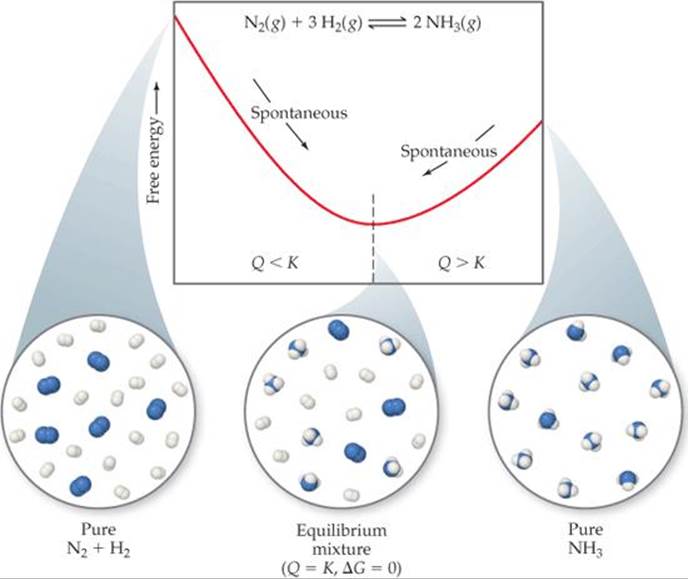
FIGURE 19.17 Free energy and approaching equilibrium. In the reaction 
, if the reaction mixture has too much N2 and H2 relative to NH3 (left), the equilibrium lies too far to the left (Q < K) and NH3 forms spontaneously. If there is too much NH3 in the mixture (right), the equilibrium lies too far to the right (Q > K) and the NH3 decomposes spontaneously into N2 and H2.
GIVE IT SOME THOUGHT
What are the criteria for spontaneity
a. in terms of entropy and
b. in terms of free energy?
This is a good time to remind ourselves of the significance of the reaction quotient, Q, for a system that is not at equilibrium. (Section 15.6) Recall that when Q < K, there is an excess of reactants relative to products and the reaction proceeds spontaneously in the forward direction to reach equilibrium, as noted in Figure 19.17. When Q > K, the reaction proceeds spontaneously in the reverse direction. At equilibrium Q = K.
SAMPLE EXERCISE 19.6 Calculating Free-Energy Change from ΔH°, T, and ΔS°
Calculate the standard free-energy change for the formation of NO(g) from N2(g) and O2(g) at 298 K:
given that ΔH ° = 180.7 kJ and ΔS° = 24.7 J/K. Is the reaction spontaneous under these conditions?
SOLUTION
Analyze We are asked to calculate ΔG° for the indicated reaction (given ΔH°, ΔS°, and T) and to predict whether the reaction is spontaneous under standard conditions at 298 K.
Plan To calculate ΔG°, we use Equation 19.12, ΔG° = ΔH° – TΔS°. To determine whether the reaction is spontaneous under standard conditions, we look at the sign of ΔG°.
Solve
Because ΔG° is positive, the reaction is not spontaneous under standard conditions at 298 K.
Comment Notice that we had to convert the units of the TΔS° term to kJ so that they could be added to the ΔH° term, whose units are kJ.
PRACTICE EXERCISE
Calculate ΔG ° for a reaction for which ΔH° = 24.6 kJ and ΔS° = 132 J/K at 298 K. Is the reaction spontaneous under these conditions?
Answer: ΔG° = –14.7 kJ; the reaction is spontaneous.
Standard Free Energy of Formation
Recall that we defined standard enthalpies of formation, 
, as the enthalpy change when a substance is formed from its elements under defined standard conditions. (Section 5.7) We can define standard free energies of formation, 
, in a similar way. As is summarized in 
TABLE 19.2, standard state means 1 atm pressure for gases, the pure solid for solids, and the pure liquid for liquids. For substances in solution, the standard state is normally a concentration of 1 M. (In very accurate work it may be necessary to make certain corrections, but we need not worry about these.)
TABLE 19.2 • Conventions Used in Establishing Standard Free Energies
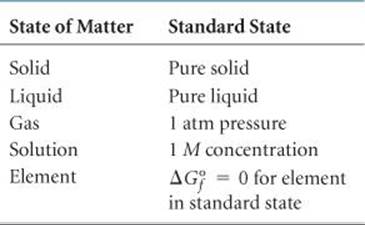
The temperature usually chosen for purposes of tabulating data is 25 °C, but we will calculate ΔG° at other temperatures as well. Just as for the standard heats of formation, the free energies of elements in their standard states are set to zero. This arbitrary choice of a reference point has no effect on the quantity in which we are interested, which is the difference in free energy between reactants and products.
A listing of standard free energies of formation is given in Appendix C.
GIVE IT SOME THOUGHT
What does the superscript ° indicate when associated with a thermodynamic quantity, as in 
H°,S°, or ΔG°?
Standard free energies of formation are useful in calculating the standard free-energy change for chemical processes. The procedure is analogous to the calculation of H° (Equation 5.31) and S° (Equation 19.8):
SAMPLE EXERCISE 19.7 Calculating Standard Free-Energy Change from Free Energies of Formation
(a) Use data from Appendix C to calculate the standard free-energy change for the reaction P4(g) + 6 Cl2(g) → 4 PCl3 (g) run at 298 K.
(b) What is G° for the reverse of this reaction?
SOLUTION
Analyze We are asked to calculate the free-energy change for a reaction and then to determine the free-energy change for the reverse reaction.
Plan We look up the free-energy values for the products and reactants and use Equation 19.14: We multiply the molar quantities by the coefficients in the balanced equation and subtract the total for the reactants from that for the products.
Solve
(a) Cl2(g) is in its standard state, so 
is zero for this reactant. P4(g), however, is not in its standard state, so is not zero for this reactant. From thebalanced equation and values from Appendix C, we have
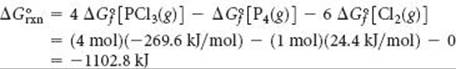
That ΔG° is negative tells us that a mixture of P4(g), Cl2(g), and PCl3(g) at 25 °C, each present at a partial pressure of 1 atm, would react spontaneously in the forward direction to form more PCl3. Remember, however, that the value of ΔG° tells us nothing about the rate at which the reaction occurs.
(b) When we reverse the reaction, we reverse the roles of the reactants and products. Thus, reversing the reaction changes the sign of ΔG in Equation 19.14, just as reversing the reaction changes the sign of ΔH. (Section 5.4) Hence, using the result from part (a), we have
PRACTICE EXERCISE
Use data from Appendix C to calculate ΔG° at 298 K for the combustion of methane: 
Answer: –800.7 kJ
SAMPLE EXERCISE 19.8 Estimating and Calculating ΔG°
In Section 5.7 we used Hess's law to calculate ΔH° for the combustion of propane gas at 298 K:
(a) Without using data from Appendix C, predict whether ΔG° for this reaction is more negative or less negative than ΔH°. (b) Use data from Appendix C to calculate ΔG° for the reaction at 298 K. Is your prediction from part (a) correct?
SOLUTION
Analyze In part (a) we must predict the value for ΔG° relative to that for ΔH° on the basis of the balanced equation for the reaction. In part (b) we must calculate the value for ΔG° and compare this value with our qualitative prediction.
Plan The free-energy change incorporates both the change in enthalpy and the change in entropy for the reaction (Equation 19.11), so under standard conditions
To determine whether ΔG° is more negative or less negative than ΔH°, we need to determine the sign of the term TΔS°. Because T is the absolute temperature, 298 K, it is always a positive number. We can predict the sign of ΔS° by looking at the reaction.
Solve
(a) The reactants are six molecules of gas, and the products are three molecules of gas and four molecules of liquid. Thus, the number of molecules of gas has decreased significantly during the reaction. By using the general rules discussed in Section 19.3, we expect a decrease in the number of gas molecules to lead to a decrease in the entropy of the system—the products have fewer possible microstates than the reactants. We therefore expect ΔS° and TΔS° to be negative. Because we are subtracting TΔS°, which is a negative number, we predict that ΔG° is less negative than ΔH°.
(b) Using Equation 19.14 and values from Appendix C, we have
Notice that we have been careful to use the value of for H2O(l). As in calculating H values, the phases of the reactants and products are important. As we predicted, ΔG° is less negative than H° because of the decrease in entropy during the reaction.
PRACTICE EXERCISE
For the combustion of propane at 298 K,
do you expect ΔG° to be more negative or less negative than H°?
Answer: more negative
A CLOSER LOOK
WHAT'S “FREE” ABOUT FREE ENERGY?
The Gibbs free energy is a remarkable thermo-dynamic quantity. Because so many chemical reactions are carried out under conditions of near-constant pressure and temperature, chemists, biochemists, and engineers use the sign and magnitude of ΔG as exceptionally useful tools in the design of chemical and biochemical reactions. We will see examples of the usefulness of ΔG throughout the remainder of this chapter and this text.
Two common questions often arise when one first learns about the Gibbs free energy: Why does the sign of ΔG tell us about the spontaneity of reactions? And what is “free” about free energy? We address these two questions here by using concepts discussed in Chapter 5 and earlier in this chapter.
In Section 19.2 we saw that the second law of thermodynamics governs the spontaneity of processes. In order to apply the second law (Equations 19.4), however, we must determine ΔSuniv, which is often difficult to evaluate. When T and P are constant, however, we can relate ΔSuniv to the changes in entropy and enthalpy of just the system by substituting the Equation 19.9 expression for ΔSsurr in Equation 19.4:
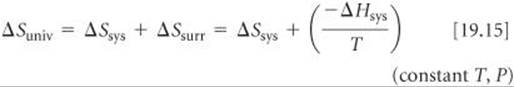
Thus, at constant temperature and pressure, the second law becomes
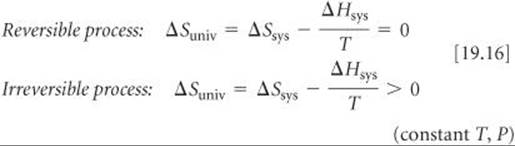
Now we can see the relationship between ΔGsys (which we call simply ΔG) and the second law. From Equation 19.11 we know that ΔG = ΔHsys–TΔSsys. If we multiply Equations 19.16 by –T and rearrange, we reach the following conclusion:
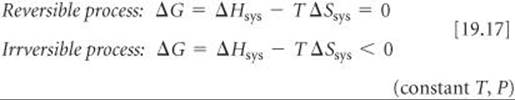
Equations 19.17 allow us to use the sign of ΔG to conclude whether a reaction is spontaneous, nonspontaneous, or at equilibrium. When ΔG < 0, a process is irreversible and, therefore, spontaneous. When ΔG = 0, the process is reversible and, therefore, at equilibrium. If a process has ΔG >0, then the reverse process will have ΔG < 0; thus, the process as written is nonspontaneous but its reverse reaction will be irreversible and spontaneous.
The magnitude of ΔG is also significant. A reaction for which ΔG is large and negative, such as the burning of gasoline, is much more capable of doing work on the surroundings than is a reaction for which ΔG is small and negative, such as ice melting at room temperature. In fact, thermodynamics tells us that the change in free energy for a process, ΔG, equals the maximum useful work that can be done by the system on its surroundings in a spontaneous process occurring at constant temperature and pressure:
(Remember our sign convention from Table 5.1: Work done by a system is negative.) In other words, ΔG gives the theoretical limit to how much work can be done by a process.
The relationship in Equation 19.18 explains why ΔG is called free energy—it is the portion of the energy change of a spontaneous reaction that is free to do useful work. The remainder of the energy enters the environment as heat. For example, the theoretical maximum work obtained for the combustion of gasoline is given by the value of ΔG for the combustion reaction. On average, standard internal combustion engines are inefficient in utilizing this potential work—more than 60% of the potential work is lost (primarily as heat) in converting the chemical energy of the gasoline to mechanical energy to move the vehicle (
FIGURE 19.18). When other losses are considered—idling time, braking, aerodynamic drag, and so forth—only about 15% of the potential work from the gasoline is used to move the car. Advances in automobile design—such as hybrid technology, efficient diesel engines, and new lightweight materials—have the potential to increase the percentage of useful work obtained from the gasoline.
For nonspontaneous processes (ΔG > 0), the free-energy change is a measure of the minimum amount of work that must be done to cause the process to occur. In actuality, we always need to do more than this theoretical minimum amount because of the inefficiencies in the way the changes occur.
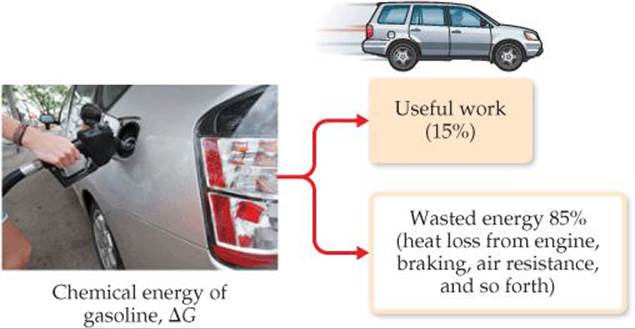
FIGURE 19.18 Energy losses in automobiles. Very little of the chemical energy of gasoline is actually used as work to move a typical automobile.