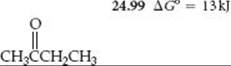CHEMISTRY THE CENTRAL SCIENCE
ANSWERS TO SELECTED EXERCISES
CHAPTER 1
1.1 (a) Pure element: i (b) mixture of elements: v, vi (c) pure compound: iv (d) mixture of an element and a compound: ii, iii
1.3 This kind of separation based on solubility differences is called extraction. The insoluble grounds are then separated from the coffee solution by filtration.
1.5 (a) The aluminum sphere is lightest, then nickel, then silver. (b) The platinum sphere is largest, then gold, then lead.
1.7 (a) 7.5 cm; two significant figures (sig figs) (b) 72 mi/hr (inner scale, two significant figures) or 115 km/hr (outer scale, three significant figures)
1.9 Arrange the conversion factor so that the given unit cancels and the desired unit is in the correct position.
1.11 (a) Heterogeneous mixture (b) homogeneous mixture (heterogeneous if there are undissolved particles) (c) pure substance (d) pure substance.
1.13 (a) S (b) Au (c) K (d) Cl (e) Cu (f) uranium (g) nickel (h) sodium (i) aluminum (j) silicon
1.15 C is a compound; it contains both carbon and oxygen. A is a compound; it contains at least carbon and oxygen. B is not defined by the data given; it is probably also a compound because few elements exist as white solids.
1.17 Physical properties: silvery white; lustrous; melting point = 649 °C; boiling point 1105 °C; density at 20 °C = 1.738 g/cm3; pounded into sheets; drawn into wires; good conductor. Chemical properties: burns in air; reacts with Cl2.
1.19 (a) Chemical (b) physical (c) physical (d) chemical (e) chemical
1.21 (a) Add water to dissolve the sugar; filter this mixture, collecting the sand on the filter paper and the sugar water in the flask. Evaporate water from the flask to recover solid sugar. (b) Allow the mixture to settle so that there are two distinct layers. Carefully pour off most of the top oil layer. After the layers reform, use a dropper to remove any remaining oil. Vinegar is in the original vessel and oil is in a second container.
1.23 (a) 1 × 10–1 (b) 1 × 10–2 (c) 1 × 10–15 (d) 1 × 10–6 (e) 1 × 106 (f) 1 × 103 (g) 1 × 10–9 (h) 1 × 10–3 (i) 1 × 10–12
1.25 (a) 22 °C (b) 422.1 °F (c) 506 K (d) 107 °C (e) 1644 K (f) –459.67 °F
1.27 (a) 1.62 g/mL. Tetrachloroethylene, 1.62 g/mL, is more dense than water, 1.00 g/mL; tetrachloroethylene will sink rather than float on water. (b) 11.7 g
1.29 (a) Calculated density = 0.866 g/mL. The substance is probably toluene, density = 0.866 g/mL. (b) 40.4 mL ethylene glycol (c) 1.11 × 103 g nickel
1.31 28 Pg
1.33 Exact: (c), (d), and (f)
1.35 (a) 3 (b) 2 (c) 5 (d) 3 (e) 5 (f) 1
1.37 (a) 1.025 × 102 (b) 6.570 × 105 (c) 8.543 × 10–3 (d) 2.579 × 10–4 (e) –3.572 × 10–2
1.39 (a) 17.00 (b) 812.0 (c) 8.23 × 103 (d) 8.69 × 10–2
1.41 5 significant figures
1.43 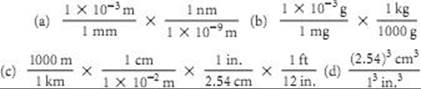
1.45 (a) 54.7 km/hr (b) 1.3 × 103 gal (c) 46.0 m (d) 0.984 in/hr
1.47 (a) 4.32 × 105 s (b) 88.5 m (c) $0.499/L (d) 46.6 km/hr (e) 1.420 L/s (f) 707.9 cm3
1.49 (a) 1.2 × 102 L (b) 5 × 102 mg (c) 19.9 mi/gal (2 × 101 mi/gal for 1 significant figure) (d) 26 mL/g (3 × 101 mL/g for 1 significant figure)
1.51 64 kg air
1.53 14-in. shoe < 57-cm string < 1.1-m pipe
1.55 $6 × 104
1.59 8.47 g O; the law of constant composition
1.62 (a) Volume (b) area (c) volume (d) density (e) time (f) length (g) temperature
1.65 (a) 1.13 × 105 quarters (b) 6.41 × 105 g (c) $2.83 × 104 (d) 4.13 × 108 stacks
1.68 The most dense liquid, Hg, will sink; the least dense, cyclohexane, will float; H2O will be in the middle.
1.71 density of solid = 1.63 g/mL
1.74 (a) Density of peat = 0.13 g/cm3, density of soil = 2.5 g/cm3. It is not correct to say that peat is “lighter” than topsoil. Volumes must be specified in order to compare masses. (b) Buy 16 bags of peat (more than 15 are needed). (Results to 1 significant figure are not meaningful.)
1.77 The inner diameter of the tube is 1.13 cm.
1.79 The separation is successful if two distinct spots are seen on the paper. To quantify the characteristics of the separation, calculate a reference value for each spot: distance traveled by spot/distance traveled by solvent. If the values for the two spots are fairly different, the separation is successful.
CHAPTER 2
2.1 (a) The path of the charged particle bends because the particle is repelled by the negatively charged plate and attracted to the positively charged plate. (b) (–) (c) increase (d) decrease
2.4 The particle is an ion. ![]()
2.6 Formula: IF5; name: iodine pentafluoride; the compound is molecular.
2.9 Postulate 4 of the atomic theory states that the relative number and kinds of atoms in a compound are constant, regardless of the source. Therefore, 1.0 g of pure water should always contain the same relative amounts of hydrogen and oxygen, no matter where or how the sample is obtained.
2.11 (a) 0.5711 g O/1 g N; 1.142 g O/1 g N; 2.284 g O/1 g N; 2.855 g O/1 g N (b) The numbers in part (a) obey the law of multiple proportions. Multiple proportions arise because atoms are the indivisible entities combining, as stated in Dalton's atomic theory.
2.13 (1) Electric and magnetic fields deflected the rays in the same way they would deflect negatively charged particles. (2) A metal plate exposed to cathode rays acquired a negative charge.
2.15 (a) Most of the volume of an atom is empty space in which electrons move. Most alpha particles passed through this space. (b) The few alpha particles that hit the massive, positively charged gold nuclei were strongly repelled and deflected back in the direction they came from. (c) Because the Be nuclei have a smaller volume and a smaller positive charge than the Au nuclei, fewer alpha particles will be scattered and fewer will be strongly back scattered.
2.17 (a) 0.135 nm; 1.35 × 102 or 135 pm (b) 3.70 × 106 Au atoms (c) 1.03 × 10–23 cm3
2.19 (a) Proton, neutron, electron (b) proton = 1+, neutron = 0, electron = 1– (c) The neutron is most massive. (The neutron and proton have very similar masses.) (d) The electron is least massive.
2.21 (a) Atomic number is the number of protons in the nucleus of an atom. Mass number is the total number of nuclear particles, protons plus neutrons, in an atom. (b) mass number
2.23 (a) 40Ar: 18 p, 22 n, 18 e (b) 65Zn: 30 p, 35 n, 30 e (c) 70Ga: 31 p, 39 n, 31 e (d) 80Br: 35 p, 45 n, 35 e (e) 184W: 74 p, 110 n, 74 e (f) 243Am: 95 p, 148 n, 95 e
2.25
2.27 ![]() Atomic weights are average atomic masses, the sum of the mass of each naturally occurring isotope of an element times its fractional abundance. Each B atom will have the mass of one of the naturally occurring isotopes, while the “atomic weight” is an average value.
Atomic weights are average atomic masses, the sum of the mass of each naturally occurring isotope of an element times its fractional abundance. Each B atom will have the mass of one of the naturally occurring isotopes, while the “atomic weight” is an average value.
2.31 63.55 amu
2.33 (a) In Thomson's cathode-ray experiments and in mass spec-trometry, a stream of charged particles is passed through the poles of a magnet. The charged particles are deflected by the magnetic field according to their mass and charge. (b) The x-axis label is atomic weight, and the y-axis label is signal intensity. (c) Uncharged particles are not deflected in a magnetic field. The effect of the magnetic field on charged moving particles is the basis of their separation by mass.
2.35 (a) average atomic mass = 24.31 amu
(b)

2.37 (a) Cr, 24 (metal) (b) He, 2 (nonmetal) (c) P, 15 (nonmetal) (d) Zn, 30 (metal) (e) Mg, 12 (metal) (f) Br, 35 (nonmetal) (g) As, 33 (metalloid)
2.39 (a) K, alkali metals (metal) (b) I, halogens (nonmetal) (c) Mg, alkaline earth metals (metal) (d) Ar, noble gases (nonmetal) (e) S, chalcogens (nonmetal)
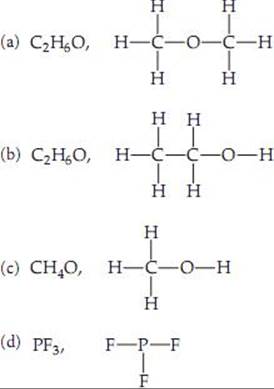
2.41 An empirical formula shows the simplest mole ratio of elements in a compound. A molecular formula shows the exact number and kinds of atoms in a molecule. A structural formula shows which atoms are attached to which.
2.43 (a) AlBr3 (b) C4H5 (c) C2H4O (d) P2O5 (e) C3H2Cl (f) BNH2
2.45 (a) 6 (b) 6 (c) 12
2.47
2.49
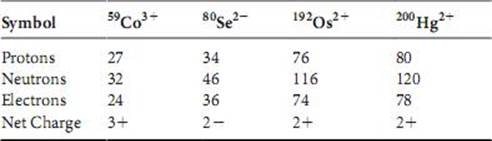
2.51 (a) Mg2+ (b) Al3+ (c) K+ (d) S2– (e) F–
2.53 (a) GaF3, gallium(III) fluoride (b) LiH, lithium hydride (c) AlI3, aluminum iodide (d) K2S, potassium sulfide
2.55 (a) CaBr2 (b) K2CO3 (c) Al(CH3COO)3 (d) (NH4)2SO4 (e) Mg3(PO4)2
2.57
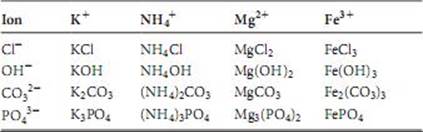
2.59 Molecular: (a) B2H6 (b) CH3OH (f) NOCl (g) NF3. Ionic: (c) LiNO3 (d) Sc2O3 (e) CsBr (h) Ag2SO4
2.61 (a) ClO2– (b) Cl– (c) ClO3– (d) ClO4– (e) ClO–
2.63 (a) calcium, 2+; oxide, 2– (b) sodium, 1+; sulfate, 2– (c) potassium, 1+; perchlorate, 1– (d) iron, 2+, nitrate, 1– (e) chromium, 3+; hydroxide, 1–
2.65 (a) lithium oxide (b) iron(III) chloride (ferric chloride) (c) sodium hypochlorite (d) calcium sulfite (e) copper(II) hydroxide (cupric hydroxide) (f) iron(II) nitrate (ferrous nitrate) (g) calcium acetate (h) chromium(III) carbonate (chromic carbonate) (i) potassium chromate (j) ammonium sulfate
2.67 (a) Al(OH)3 (b) K2SO4 (c) Cu2O (d) Zn(NO3)2 (e) HgBr2 (f) Fe2(CO3)3 (g) NaBrO
2.69 (a) Bromic acid (b) hydrobromic acid (c) phosphoric acid (d) HClO (e) HIO3 (f) H2SO3
2.71 (a) Sulfur hexafluoride (b) iodine pentafluoride (c) xenon trioxide (d) N2O4 (e) HCN (f) P4S6
2.73 (a) ZnCO3, ZnO, CO2 (b) HF, SiO2, SiF4, H2O (c) SO2, H2O, H2SO3 (d) PH3 (e) HClO4, Cd, Cd(ClO4)2 (f) VBr3
2.75 (a) A hydrocarbon is a compound composed of the elements hydrogen and carbon only.
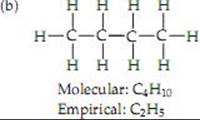
2.77 (a) Functional groups are groups of specific atoms that are constant from one molecule to the next. (b) — OH
2.79 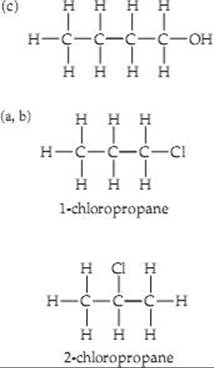
2.82 (a) 2 protons, 1 neutron, 2 electrons (b) tritium, 3H, is more massive. (c) A precision of 1 × 10–27 g would be required to differentiate between 3H+ and 3He+.
2.84 Arrangement A, 4.1 × 1014 atoms/cm2 (b) Arrangement B, 4.7 × 1014 atoms/cm2 (c) The ratio of atoms going from arrangement B to arrangement A is 1.2 to 1. In three dimensions, arrangement B leads to a greater density for Rb metal.
2.87 (a) ![]() (b) All isotopes are atoms of the same element, oxygen, with the same atomic number, 8 protons in the nucleus and 8 electrons. We expect their electron arrangements to be the same and their chemical properties to be very similar. Each has a different number of neutrons, a different mass number, and a different atomic mass.
(b) All isotopes are atoms of the same element, oxygen, with the same atomic number, 8 protons in the nucleus and 8 electrons. We expect their electron arrangements to be the same and their chemical properties to be very similar. Each has a different number of neutrons, a different mass number, and a different atomic mass.
2.90 (a) ![]() 31 protons, 38 neutrons;
31 protons, 38 neutrons; ![]() 31 protons, 40 neutrons (b)
31 protons, 40 neutrons (b) ![]()
![]()
2.93 (a) 5 significant figures (b) An electron is 0.05444% of the mass of an 1H atom.
2.96 Strontium is an alkaline earth metal, similar in chemical properties to calcium and magnesium. Harmful strontium closely mimics essential calcium and magnesium, then behaves badly when the body tries to use it as it uses calcium and magnesium.
2.98 (a) Nickel(II) oxide, 2+ (b) manganese(IV) oxide, 4+ (c) chromium(III) oxide, 3+ (d) molybdenum(VI) oxide, 6+
2.101 (a) Perbromate ion (b) selenite ion (c) AsO43– (d) HTeO4–
2.104 (a) Potassium nitrate (b) sodium carbonate (c) calcium oxide (d) hydrochloric acid (e) magnesium sulfate (f) magnesium hydroxide
CHAPTER 3
3.1 Equation (a) best fits the diagram.
3.3 (a) NO2 (b) No, because we have no way of knowing whether the empirical and molecular formulas are the same. NO2 represents the simplest ratio of atoms in a molecule but not the only possible molecular formula.
3.5 (a) C2H5NO2 (b) 75.0 g/mol (c) 225 g glycine (d) Mass %N in glycine is 18.7%.
3.7
N2 + 3 H2![]() 2 NH3. Eight N atoms (4 N2 molecules) require 24H atoms (12 H2 molecules) for complete reaction. Only 9 H2 molecules are available, so H2 is the limiting reactant. Nine H2 molecules (18 H atoms) determine that 6 NH3 molecules are produced. One N2 molecule is in excess.
2 NH3. Eight N atoms (4 N2 molecules) require 24H atoms (12 H2 molecules) for complete reaction. Only 9 H2 molecules are available, so H2 is the limiting reactant. Nine H2 molecules (18 H atoms) determine that 6 NH3 molecules are produced. One N2 molecule is in excess.
3.9 (a) Conservation of mass (b) Subscripts in chemical formulas should not be changed when balancing equations, because changing the subscript changes the identity of the compound (law of constant composition). (c) H2O(l), H2O(g), NaCl(aq), NaCl(s)
3.11 (a) 2 CO(g) + O2(g) ![]() 2 CO2(g)
2 CO2(g)
(b) N2O5(g) + H2O(l) ![]() 2 HNO3(aq)
2 HNO3(aq)
(c) CH4(g) + 4 Cl2(g) ![]() CCl4(l) + 4 HCl(g)
CCl4(l) + 4 HCl(g)
(d) Al4C3(s) + 12 H2O(l) ![]() 4 Al(OH)3(s) + 3 CH4(g)
4 Al(OH)3(s) + 3 CH4(g)
(e) 2 C5H10O2(l) + 13 O2(g) ![]() 10 CO2(g) + 10 H2O(g)
10 CO2(g) + 10 H2O(g)
(f) 2 Fe(OH)3(s) + 3 H2SO4(aq) ![]() Fe2(SO4)3(aq) + 6 H2O(l)
Fe2(SO4)3(aq) + 6 H2O(l)
(g) Mg3N2(s) + 4 H2SO4(aq) ![]() 3 MgSO4(aq) + (NH4)2SO4(aq)
3 MgSO4(aq) + (NH4)2SO4(aq)
3.13 (a) CaC2(s) + 2 H2O(l) ![]() Ca(OH)2(aq) + C2H2(g)
Ca(OH)2(aq) + C2H2(g)
(b) 2 KClO3(s) ![]() 2 KCl(s) + 3 O2(g)
2 KCl(s) + 3 O2(g)
(c) Zn(s) + H2SO4(aq) ![]() ZnSO4(aq) + H2(g)
ZnSO4(aq) + H2(g)
(d) PCl3(l) + 3 H2O(l) ![]() H3PO3(aq) + 3 HCl(aq)
H3PO3(aq) + 3 HCl(aq)
(e) 3 H2S(g) + 2 Fe(OH)3(s) ![]() Fe2S3(s) + 6 H2O(g)
Fe2S3(s) + 6 H2O(g)
3.15 (a) Determine the formula by balancing the positive and negative charges in the ionic product. All ionic compounds are solids.
2 Na(s) + Br2(l) ![]() 2 NaBr(s) (b) The second reactant is O2(g).
2 NaBr(s) (b) The second reactant is O2(g).
The products are CO2(g) and H2O(l).
2 C6H6(l) + 15 O2(g) ![]() 12 CO2(g) + 6 H2O(l)
12 CO2(g) + 6 H2O(l)
3.17 (a) Mg(s) + Cl2(g) ![]() MgCl2(s)
MgCl2(s)
(b) BaCO3(s) ![]() BaO(s) + CO2(g)
BaO(s) + CO2(g)
(c) C8H8(l) + 10 O2(g) ![]() 8 CO2(g) + 4 H2O(l)
8 CO2(g) + 4 H2O(l)
(d) C2H6O(g) + 3 O2(g) ![]() 2 CO2(g) + 3 H2O(l)
2 CO2(g) + 3 H2O(l)
3.19 (a) 2 C3H6(g) + 9 O2(g) ![]() 6 CO2(g) + 6 H2O(g) combustion
6 CO2(g) + 6 H2O(g) combustion
(b) NH4NO3(s) ![]() N2O(g) + 2 H2O(g) decomposition
N2O(g) + 2 H2O(g) decomposition
(c) C5H6O(l) + 6 O2(g) ![]() 5 CO2(g) + 3 H2O(g) combustion
5 CO2(g) + 3 H2O(g) combustion
(d) N2(g) + 3 H2(g) ![]() 2 NH3(g) combination
2 NH3(g) combination
(e) K2O(s) + H2O(l) ![]() 2 KOH(aq) combination
2 KOH(aq) combination
3.21 (a) 63.0 amu (b) 158.0 amu (c) 310.3 amu (d) 60.1 amu (e) 235.7 amu (f) 392.3 amu (g) 137.5 amu
3.23 (a) 16.8% (b) 16.1% (c) 21.1% (d) 28.8% (e) 27.2% (f) 26.5%
3.25 (a) 79.2% (b) 63.2% (c) 64.6%
3.27 (a) 6.022 × 1023 (b) The formula weight of a substance in amu has the same numerical value as the molar mass expressed in grams.
3.29 23 g Na contains 1 mol of atoms; 0.5 mol H2O contains 1.5 mol atoms; 6.0 × 1023 N2 molecules contain 2 mol of atoms.
3.31 4.37 × 1025 kg (assuming 160 lb has 3 significant figures). One mole of people weighs 7.31 times as much as Earth.
3.33 (a) 35.9 g C12H22O11 (b) 0.75766 mol Zn(NO3)2 (c) 6.0 × 1017 CH3CH2OH molecules (d) 2.47 × 1023 N atoms
3.35 (a) 0.373 g (NH4)3PO4 (b) 5.737 × 10–3 mol Cl– (c) 0.248 g C8H10N4O2 (d) 387 g cholesterol/mol
3.37 (a) Molar mass = 162.3 g(b) 3.08 × 10–5 mol allicin (c) 1.86 × 1019 allicin molecules (d) 3.71 × 1019 S atoms
3.39 (a) 2.500 × 1021 H atoms (b) 2.083 × 1020 C6H12O6 molecules (c) 3.460 × 10–4 mol C6H12O6 (d) 0.06227 g C6H12O63.41 3.2 × 10–8 mol C2H3Cl/L; 1.9 × 1016 molecules/L
3.43 (a) C2H6O (b) Fe2O3 (c) CH2O
3.45 (a) CSCl2 (b) C3OF6 (c) Na3AlF6
3.47 31 g/mol
3.49 (a) C6H12 (b) NH2Cl
3.51 (a) Empirical formula, CH; molecular formula, C8H8 (b) empirical formula, C4H5N2O; molecular formula, C8H10N4O2 (c) empirical formula and molecular formula, NaC5H8O4N
3.53 (a) C7H8 (b) The empirical and molecular formulas are C10H20O.
3.55 The molecular formula from the model is C8H16O2, which corresponds to an empirical formula of C4H8O. The results from combustion analysis are consistent with this empirical formula.
3.57 x = 10; Na2CO3 • 10 H2O
3.59 If the equation is not balanced, the mole ratios derived from the coefficients will be incorrect and lead to erroneous calculated amounts of products.
3.61 (a) 2.40 mol HF (b) 5.25 g NaF (c) 0.610 g Na2SiO3
3.63 (a) Al(OH)3(s) + 3 HCl(aq) ![]() AlCl3(aq) + 3 H2O(l) (b) 0.701 g HCl (c) 0.855 g AlCl3; 0.347 g H2O (d) Mass of reactants = 0.500 g + 0.701 g = 1.201 g; mass of products = 0.855 g + 0.347 g = 1.202 g. Mass is conserved, within the precision of the data.
AlCl3(aq) + 3 H2O(l) (b) 0.701 g HCl (c) 0.855 g AlCl3; 0.347 g H2O (d) Mass of reactants = 0.500 g + 0.701 g = 1.201 g; mass of products = 0.855 g + 0.347 g = 1.202 g. Mass is conserved, within the precision of the data.
3.65 (a) Al2S3(s) + 6 H2O(l) ![]() 2 Al(OH)3(s) + 3 H2S(g) (b) 14.7 g Al(OH)3
2 Al(OH)3(s) + 3 H2S(g) (b) 14.7 g Al(OH)3
3.67 (a) 2.25 mol N2 (b) 15.5 g NaN3 (c) 548 g NaN3
3.69 (a) 5.50 × 10–3 mol Al (b) 1.47 g AlBr3
3.71 (a) The limiting reactant determines the maximum number of product moles resulting from a chemical reaction; any other reactant is an excess reactant. (b) The limiting reactant regulates the amount of products because it is completely used up during the reaction; no more product can be made when one of the reactants is unavailable. (c) Combining ratios are molecule and mole ratios. Since different molecules have different masses, comparing initial masses of reactants will not provide a comparison of numbers of molecules or moles.
3.73 (a) 2255 bicycles (b) 50 frames left over, 305 wheels left over (c) the handlebars
3.75 NaOH is the limiting reactant; 0.925 mol Na2CO3 can be produced; 0.075 mol CO2 remains.
3.77 (a) NaHCO3 is the limiting reactant. (b) 0.524 g CO2 (c) 0.238 g citric acid remains
3.79 0.00 g AgNO3 (limiting reactant), 1.94 g Na2CO3, 4.06 g Ag2CO3, 2.50 g NaNO3
3.81 (a) The theoretical yield is 60.3 g C6H5Br. (b) 70.1% yield
3.83 28 g S8 actual yield
3.85 (a) C2H4O2(l) + 2 O2(g) ![]() 2 CO2(g) + 2 H2O(l) (b) Ca(OH)2(s)
2 CO2(g) + 2 H2O(l) (b) Ca(OH)2(s) ![]() CaO(s) + H2O(g) (c) Ni(s) + Cl2(g)
CaO(s) + H2O(g) (c) Ni(s) + Cl2(g) ![]() NiCl2(s)
NiCl2(s)
3.89 (a) 8 × 10–20 g Si (b) 2 × 103 Si atoms (with 2 significant figures, 1700 Si atoms) (c) 1 × 103 Ge atoms (with 2 significant figures, 1500 Ge atoms)
3.93 C8H8O3
3.97 (a) 1.19 × 10–5 mol NaI (b) 8.1 × 10–3 g NaI
3.101 7.5 mol H2 and 4.5 mol N2 present initially
3.105 6.46 × 1024 O atoms
3.107 (a) 88 kg CO2 (b) 4 × 102 (400) kg CO2
3.109(a) S(s) + O2(g) ![]() SO2(g); SO2(g) + CaO(s)
SO2(g); SO2(g) + CaO(s) ![]() CaSO3(s) (b) 7.9 × 107 g CaO (c) 1.7 × 108 g CaSO3
CaSO3(s) (b) 7.9 × 107 g CaO (c) 1.7 × 108 g CaSO3
CHAPTER 4
4.1 Diagram (c) represents Li2SO4
4.3 (a) HCOOH is a weak electrolyte. (b) HNO3 is a strong electrolyte. (c) CH3CH2OH is a nonelectrolyte.
4.5 BaCl2
4.7 (b) NO3– and (c) NH4+ will always be spectator ions.
4.9 In a redox reaction, electrons are transferred from the oxidized substance to the reduced substance. In an acid-base reaction, protons are transferred from an acid to a base.
4.11 No. Electrolyte solutions conduct electricity because the dissolved ions carry charge through the solution from one electrode to the other.
4.13 Although H2O molecules are electrically neutral, there is an unequal distribution of electrons throughout the molecule. The partially positive ends of H2O molecules are attracted to anions in the solid, while the partially negative ends are attracted to cations. Thus, both cations and anions in an ionic solid are surrounded and separated (dissolved) by H2O. We do not expect ionic compounds to be soluble in molecular liquids such as Br2(l) or Hg(l). There is a symmetrical charge distribution in Hg atoms and Br2 molecules, so there are no attractive forces to stabilize the separated ions of an ionic solid.
4.15 (a) ZnCl2(aq) ![]() Z2+(aq) + 2 Cl–(aq) (b) HNO3(aq)
Z2+(aq) + 2 Cl–(aq) (b) HNO3(aq) ![]() H+(aq) + NO3–(aq) (c) (NH4)2SO4(aq)
H+(aq) + NO3–(aq) (c) (NH4)2SO4(aq) ![]() 2 NH4+(aq) + SO42– (aq) (d) Ca(OH)(aq)
2 NH4+(aq) + SO42– (aq) (d) Ca(OH)(aq) ![]() Ca2+(aq) + 2 OH–(aq)
Ca2+(aq) + 2 OH–(aq)
4.17 HCOOH molecules, H+ ions, and HCOO– ions; HCOOH(aq) ![]() H+(aq) + HCOO–(aq)
H+(aq) + HCOO–(aq)
4.19 (a) Soluble (b) insoluble (c) soluble (d) soluble (e) soluble
4.21 (a) Na2CO3(aq) + 2 AgNO3(aq) ![]() Ag2CO3(s) + 2 NaNO3(aq) (b) No precipitate (c) FeSO4(aq) + Pb(NO3)2(aq)
Ag2CO3(s) + 2 NaNO3(aq) (b) No precipitate (c) FeSO4(aq) + Pb(NO3)2(aq) ![]() PbSO4(s) + Fe(NO3)2(aq)
PbSO4(s) + Fe(NO3)2(aq)
4.23 (a) Na+, SO42– (a) Na+, NO3– (c) NH4+, Cl–
4.25 The solution contains Pb2+.
4.27
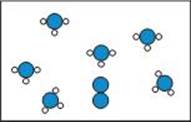
This sequence of tests would definitely identify the bottle contents.
4.29 LiOH is a strong base, HI is a strong acid, and CH3OH is a molecular compound and nonelectrolyte. The strong acid HI will have the greatest concentration of solvated protons.
4.31 (a) A monoprotic acid has one ionizable (acidic) H, whereas a diprotic acid has two. (b) A strong acid is completely ionized in aqueous solution, whereas only a fraction of weak acid molecules are ionized. (c) An acid is an H+ donor, and a base is an H+ acceptor.
4.33 When each of the strong acids in Table 4.2 dissociates, the anions formed are the same ones that normally form soluble ionic compounds (Table 4.1). The one exception is acetate, CH3COO–, the anion of a weak acid.
4.35 (a) Acid, mixture of ions and molecules (weak electrolyte) (b) none of the above, entirely molecules (nonelectrolyte) (c) salt, entirely ions (strong electrolyte) (d) base, entirely ions (strong electrolyte)
4.37 (a) H2SO3, weak electrolyte (b) C2H5OH, nonelectrolyte (c) NH3, weak electrolyte (d) KClO3, strong electrolyte (e) Cu(NO3)2, strong electrolyte
4.39 (a) 2 HBr(aq) + Ca(OH)2(aq) ![]() CaBr2(aq) + 2 H2O(l); H+(aq) + OH–(aq)
CaBr2(aq) + 2 H2O(l); H+(aq) + OH–(aq) ![]() H2O(l) (b) Cu(OH)2(s) + 2 HClO4(aq)
H2O(l) (b) Cu(OH)2(s) + 2 HClO4(aq) ![]() Cu(ClO4)2(aq) + 2 H2O(l); Cu(OH)2(s) + 2 H+(aq)
Cu(ClO4)2(aq) + 2 H2O(l); Cu(OH)2(s) + 2 H+(aq) ![]() 2 H2O(l) + Cu2+(aq) (c) Al(OH)3(s) + 3 HNO3(aq)
2 H2O(l) + Cu2+(aq) (c) Al(OH)3(s) + 3 HNO3(aq) ![]() Al(NO3)3(aq) + 3 H2O(l); Al(OH)3(s) + 3 H+(aq)
Al(NO3)3(aq) + 3 H2O(l); Al(OH)3(s) + 3 H+(aq) ![]() 3 H2O(l) + Al3+(aq)
3 H2O(l) + Al3+(aq)
4.41 (a) CdS(s) + H2SO4(aq) ![]() CdSO4(aq) + H2S(g); CdS(s) + 2H+(aq)
CdSO4(aq) + H2S(g); CdS(s) + 2H+(aq) ![]() H2S(g) + Cd2+(aq) (b) MgCO3(s) + 2 HClO4(aq)
H2S(g) + Cd2+(aq) (b) MgCO3(s) + 2 HClO4(aq) ![]() Mg(ClO4)2(aq) + H2O(l) + CO2(g); MgCO3(s) + 2 H+(aq)
Mg(ClO4)2(aq) + H2O(l) + CO2(g); MgCO3(s) + 2 H+(aq) ![]() H2O(l) + CO2(g) + Mg3+(aq)
H2O(l) + CO2(g) + Mg3+(aq)
4.43 (a) MgCO3(s)+ 2 HCl(aq) ![]() MgCl2(aq) + H2O(l) + CO2(g);
MgCl2(aq) + H2O(l) + CO2(g);
MgCO3(s) + 2 H+(aq) ![]() Mg2+(aq) + H2O(l) + CO2(g);
Mg2+(aq) + H2O(l) + CO2(g);
MgO(s) + 2 HCl(aq) ![]() MgCl2(aq) + H2O(l);
MgCl2(aq) + H2O(l);
MgO(s) + 2 H+(aq) ![]() Mg2+(aq) + H2O(l);
Mg2+(aq) + H2O(l);
Mg(OH)2(s) + 2 HCl(aq) ![]() MgCl2(aq) + 2H2O(l);
MgCl2(aq) + 2H2O(l);
Mg(OH)2(s) + 2H+(aq) ![]() Mg2+(aq) + 2 H2O(l) (b) Yes. The reaction involving magnesium carbonate, MgCO3(s), produces CO2(g), which appears as bubbles. The other two reactions are calm. (c) If excess HCl(aq) is added in each case, the identity of the ions in the clear product solution is the same. The ions are Mg2+(aq); Cl–(aq); and H+(aq).
Mg2+(aq) + 2 H2O(l) (b) Yes. The reaction involving magnesium carbonate, MgCO3(s), produces CO2(g), which appears as bubbles. The other two reactions are calm. (c) If excess HCl(aq) is added in each case, the identity of the ions in the clear product solution is the same. The ions are Mg2+(aq); Cl–(aq); and H+(aq).
4.45 (a) In terms of electron transfer, oxidation is the loss of electrons by a substance and reduction is the gain of electrons (LEO says GER). (b) Relative to oxidation numbers, when a substance is oxidized, its oxidation number increases. When a substance is reduced, its oxidation number decreases.
4.47 Metals in region A are most easily oxidized. Nonmetals in region D are least easily oxidized.
4.49 (a) +4 (b) +4 (c) +7 (d) +1 (e) 0 (f) –1
4.51 (a) N2![]() 2 NH3, N is reduced; 3 H2
2 NH3, N is reduced; 3 H2![]() 2 NH3, H is oxidized (b) Fe2+
2 NH3, H is oxidized (b) Fe2+![]() Fe, Fe is reduced; Al
Fe, Fe is reduced; Al ![]() Al3+, Al is oxidized (c) Cl2
Al3+, Al is oxidized (c) Cl2![]() 2 Cl–, Cl is reduced; 2 I–
2 Cl–, Cl is reduced; 2 I–![]() I2 I is oxidized (d) S2–
I2 I is oxidized (d) S2–![]() SO42– S is oxidized H2O2
SO42– S is oxidized H2O2![]() H2O, O is reduced
H2O, O is reduced
4.53 (a) Mn(s) + H2SO4(aq) ![]() MnSO4(aq) + H2(g);
MnSO4(aq) + H2(g);
Mn(s) + 2 H+(aq) ![]() Mn2+(aq) + H2(g)
Mn2+(aq) + H2(g)
(b) 2 Cr(s) + 6 HBr(aq) ![]() 2 CrBr3(aq) + 3 H2(g);
2 CrBr3(aq) + 3 H2(g);
2 Cr(s) + 6 H+(aq) ![]() 2 Cr3+(aq) + 3 H2(g)
2 Cr3+(aq) + 3 H2(g)
(c) Sn(s) + 2 HCl(aq) ![]() SnCl2(aq) + H2(g);
SnCl2(aq) + H2(g);
Sn(s) + 2 H+(aq) ![]() Sn2+(aq) + H2(g)
Sn2+(aq) + H2(g)
(d) 2 Al(s) + 6 HCOOH(aq) ![]() 2 Al(HCOO)3(aq) + 3 H2(g);
2 Al(HCOO)3(aq) + 3 H2(g);
2 Al(s) + 6 HCOOH(aq) ![]() 2 Al3+(aq) + 6 HCOO–(aq) + 3 H2(g)
2 Al3+(aq) + 6 HCOO–(aq) + 3 H2(g)
4.55 (a) Fe(s) + Cu(NO3)2(aq) ![]() Fe(NO3)2(aq) + Cu(s) (b) NR (c) Sn(s) + 2 HBr(aq)
Fe(NO3)2(aq) + Cu(s) (b) NR (c) Sn(s) + 2 HBr(aq) ![]() SnBr2(aq) + H2(g) (d) NR (e) 2 Al(s) + 3 CoSO4(aq)
SnBr2(aq) + H2(g) (d) NR (e) 2 Al(s) + 3 CoSO4(aq) ![]() Al2(SO4)3(aq) + 3 Co(s)
Al2(SO4)3(aq) + 3 Co(s)
4.57 (a) i. Zn(s) + Cd2+(aq) ![]() Cd(s) + Zn2+(aq);
Cd(s) + Zn2+(aq);
ii. Cd(s) + Ni2+(aq) ![]() Ni(s) + Cd2+(aq) (b) Cd is between Zn and Ni on the activity series. (c) Place an iron strip in CdCl2(aq). If Cd(s) is deposited, Cd is less active than Fe; if there is no reaction, Cd is more active than Fe. Do the same test with Co if Cd is less active than Fe or with Cr if Cd is more active than Fe.
Ni(s) + Cd2+(aq) (b) Cd is between Zn and Ni on the activity series. (c) Place an iron strip in CdCl2(aq). If Cd(s) is deposited, Cd is less active than Fe; if there is no reaction, Cd is more active than Fe. Do the same test with Co if Cd is less active than Fe or with Cr if Cd is more active than Fe.
4.59 (a) Intensive; the ratio of amount of solute to total amount of solution is the same, regardless of how much solution is present. (b) The term 0.50 mol HCl defines an amount (~18 g) of the pure substance HCl. The term 0.50 M HCl is a ratio; it indicates that there is 0.50 mol of HCl solute in 1.0 liter of solution.
4.61 (a) 1.17 M ZnCl2 (b) 0.158 mol HNO3 (c) 54.2 mL of 6.00 M NaOH
4.63 16 g Na+(aq)
4.65 BAC of 0.08 = 0.02 M CH3CH2OH (alcohol)
4.67 (a) 5.21 g KBr (b) 0.06537 M Ca(NO3)2 (c) 10.2 mL of 1.50 M Na3PO4
4.69 (a) 0.15 M K2CrO4 has the highest K+ concentration. (b) 30.0 mL of 0.15 M K2CrO4 has more K+ ions.
4.71 (a) 0.25M Na+, 0.25M NO3– (b) 1.3 × 10–2M Mg2+, 1.3 × 10–2M SO42– (c) 0.0150 M C6H12O6 (d) 0.111M Na+, 0.111M Cl–, 0.0292M NH4+, 0.0146M CO32–
4.73 (a) 16.9 mL 14.8 M NH3 (b) 0.296 M NH3
4.75 (a) Add 21.4 g C12H22O11 to a 250-mL volumetric flask, dissolve in a small volume of water, and add water to the mark on the neck of the flask. Agitate thoroughly to ensure total mixing. (b) Thoroughly rinse, clean, and fill a 50-mL buret with the 1.50 M C12H22O11. Dispense 23.3 mL of this solution into a 350-mL volumetric container, add water to the mark, and mix thoroughly.
4.77 1.398 M CH3COOH
4.79 0.227 g KCl
4.81 (a) 38.0 mL of 0.115 M HClO4 (b) 769 mL of 0.128 M HCl (c) 0.408 M AgNO3 (d) 0.275 g KOH
4.83 27 g NaHCO3
4.85 (a) Molar mass of metal hydroxide is 103 g/mol. (b) Rb+
4.87 (a) NiSO4(aq) + 2 KOH(aq) ![]() Ni(OH)2(s) + K2SO4(aq) (b) Ni(OH)2 (c) KOH is the limiting reactant. (d) 0.927 g Ni(OH)2 (e) 0.0667 M Ni2+(aq), 0.0667 M K+(aq), 0.100M SO42–(aq)
Ni(OH)2(s) + K2SO4(aq) (b) Ni(OH)2 (c) KOH is the limiting reactant. (d) 0.927 g Ni(OH)2 (e) 0.0667 M Ni2+(aq), 0.0667 M K+(aq), 0.100M SO42–(aq)
4.89 91.40% Mg(OH)2
4.92 The precipitate is CdS(s). Na+(aq) and NO3–(aq) remain in solution, along with any excess reactant ions. The net ionic equation is Cd2+(aq) + S2–(aq) ![]() CdS(s).
CdS(s).
4.94 (a, b) Expt. 1: NR; Expt. 2: 2 Ag+(aq) + CrO42–(aq) ![]() Ag2CrO4(s) red precipitate; Expt. 3: 2 Ca2+(aq) + CrO42–(aq)
Ag2CrO4(s) red precipitate; Expt. 3: 2 Ca2+(aq) + CrO42–(aq) ![]() CaCrO4(s) yellow precipitate; Expt. 4: 2 Ag+(aq) + C2O42–(aq)
CaCrO4(s) yellow precipitate; Expt. 4: 2 Ag+(aq) + C2O42–(aq) ![]() Ag2C2O4(s) white precipitate; Expt. 5: Ca2+(aq) + C2O42–(aq)
Ag2C2O4(s) white precipitate; Expt. 5: Ca2+(aq) + C2O42–(aq) ![]() CaC2O4(s) white precipitate; Expt. 6: Ag+(aq) + Cl–(aq)
CaC2O4(s) white precipitate; Expt. 6: Ag+(aq) + Cl–(aq) ![]() AgCl(s) white precipitate.
AgCl(s) white precipitate.
4.96 4 NH3(g) + 5 O2(g) ![]() 4 NO(g) + 6 H2O(g). (a) redox reaction (b) N is oxidized, O is reduced. 2 NO(g) + O2(g)
4 NO(g) + 6 H2O(g). (a) redox reaction (b) N is oxidized, O is reduced. 2 NO(g) + O2(g) ![]() 2 NO2(g). (a) redox reaction (b) N is oxidized O is reduced. 3 NO2(g) + H2O(l)
2 NO2(g). (a) redox reaction (b) N is oxidized O is reduced. 3 NO2(g) + H2O(l) ![]() HNO3(aq) + NO(g). (a) redox reaction (b) N is both oxidized and reduced.
HNO3(aq) + NO(g). (a) redox reaction (b) N is both oxidized and reduced.
4.99 1.42 M KBr
4.100 (a) 2.2 × 10–9M Na+ (b) 1.3 × 1012 Na+ ions
4.103 (a) 1.718 M Sr(OH)2 (b) 2 HNO3(aq) + Sr(OH)2(s) ![]() Sr(NO3)2(aq) + 2 H2O(l) (c) 2.61 M HNO3
Sr(NO3)2(aq) + 2 H2O(l) (c) 2.61 M HNO3
4.106 (a) The molarmass of the acid is 136 g/mol. (b) The molecular formula is C8H8O2.
4.109 (a) Mg(OH)2(s) + 2 HNO3(aq) ![]() Mg (NO3)2(aq) + 2 H2O(l) (b) HNO3 is the limiting reactant. (c) 0.0923 mol Mg(OH)2, 0 mol HNO3, and 0.00250 mol Mg(NO3)2 are present.
Mg (NO3)2(aq) + 2 H2O(l) (b) HNO3 is the limiting reactant. (c) 0.0923 mol Mg(OH)2, 0 mol HNO3, and 0.00250 mol Mg(NO3)2 are present.
4.112 1.766% Cl– by mass
4.114 1.5 × 10–5 g Na3AsO4 in 1.00 L H2O
CHAPTER 5
5.1 (a) As the book falls, potential energy decreases and kinetic energy increases. (b) 71 J, assuming no transfer of energy as heat (c) A heavier book falling from the same shelf has greater kinetic energy when it hits the floor.
5.5 (a) No. The distance traveled to the top of a mountain depends on the path taken by the hiker. Distance is a path function, not a state function. (b) Yes. Change in elevation depends only on the location of the base camp and the height of the mountain, not on the path to the top. Change in elevation is a state function, not a path function.
5.8 (a) The sign of w is (+). (b) The internal energy of the system increases during the change; the sign of ΔE is (+).
5.11 (a) ΔHA = ΔHB + ΔHC. The diagram and equation both show that the net enthalpy change for a process is independent of path, that ΔH is a state function. (b) ΔHZ = ΔHX + ΔHY. (c) Hess's law states that the enthalpy change for net reaction Z is the sum of the enthalpy changes for stepsX and Y, regardless of whether the reaction actually occurs via this path. The diagrams are a visual statement of Hess's law.
5.13 An object can possess energy by virtue of its motion or position. Kinetic energy depends on the mass of the object and its velocity. Potential energy depends on the position of the object relative to the body with which it interacts.
5.15 (a) 1.9 × 105 J (b) 4.6 × 104 cal (c) As the automobile brakes to a stop, its speed (and hence its kinetic energy) drops to zero. The kinetic energy of the automobile is primarily transferred to friction between brakes and wheels and somewhat to deformation of the tire and friction between the tire and road.
5.17 1 Btu = 1054 J
5.19 (a) The system is the well-defined part of the universe whose energy changes are being studied. (b) A closed system can exchange heat but not mass with its surroundings. (c) Any part of the universe not part of the system is called the surroundings.
5.21 (a) Work is a force applied over a distance. (b) The amount of work done is the magnitude of the force times the distance over which it is applied. w = F × d.
5.23 (a) Gravity; work is done because the force of gravity is opposed and the pencil is lifted. (b) Mechanical force; work is done because the force of the coiled spring is opposed as the spring is compressed over a distance.
5.25 (a) In any chemical or physical change, energy can be neither created nor destroyed; energy is conserved. (b) The internal energy (E) of a system is the sum of all the kinetic and potential energies of the system components. (c) Internal energy of a closed system increases when work is done on the system and when heat is transferred to the system.
5.27 (a) ΔE = –0.077 kJ, endothermic (b) ΔE = –22.1 kJ, exothermic (c) ΔE = 7.25 kJ, endothermic
5.29 (a) Since no work is done by the system in case (2), the gas will absorb most of the energy as heat; the case (2) gas will have the higher temperature. (b) In case (2) w = 0 and q = 100 J. In case (1) energy will be used to do work on the surroundings (–w), but some will be absorbed as heat (+q). (c) ΔE is greater for case (2) because the entire 100 J increases the internal energy of the system rather than a part of the energy doing work on the surroundings.
5.31 (a) A state function is a property that depends only on the physical state (pressure, temperature, etc.) of the system, not on the route used to get to the current state. (b) Internal energy is a state function; heat is not a state function. (c) Volume is a state function. The volume of a system depends only on conditions (pressure, temperature, amount of substance), not the route or method used to establish that volume.
5.33 (a) ΔH is usually easier to measure than ΔE because at constant pressure, ΔH = qp. The heat flow associated with a process at constant pressure can easily be measured as a change in temperature, while measuring ΔE requires a means to measure both q and w. (b) H is a static quantity that depends only on the specific conditions of the system. q is an energy change that, in the general case, does depend on how the change occurs. We can equate change in enthalpy, ΔH, with heat, qp, only for the specific conditions of constant pressure and exclusively P-V work. (c) The process is endothermic.
5.35 At constant pressure, ΔE = ΔH – P ΔV. The values of either P and ΔV or T and Δn must be known to calculate ΔE from ΔH.
5.37 ΔE = 1.47 kJ; ΔH = 0.824 kJ
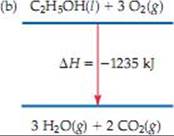
5.39 (a) C2H5OH(l) + 3 O2(g) ![]() 3 H2O + 2 CO2(g), ΔH = –1235 kj
3 H2O + 2 CO2(g), ΔH = –1235 kj
5.41 (a) ΔH = –142.3 kJ/mol O3(g) (b) 2 O3(g) has the higher enthalpy.
5.43 (a) Exothermic (b) –87.9 kJ heat transferred (c) 15.7 g MgO produced (d) 602 kJ heat absorbed
5.45 (a) –29.5 kJ (b) –4.11 kJ (c) 60.6 J
5.47 (a) ΔH = 726.5 kJ (b) ΔH = –1453 kJ (c) The exothermic forward reaction is more likely to be thermodynamically favored. (d) Vaporization is endothermic. If the product were H2O(g), the reaction would be more endothermic and would have a less negative ΔH.
5.49 (a) J/mol-°C or J/mol-K (b) J/g-°C or J/g-K (c) To calculate heat capacity from specific heat, the mass of the particular piece of copper pipe must be known.
5.51 (a) 4.184 J/g-K (b) 75.40 J/mol-°C (c) 774 J/°C (d) 904 kJ
5.53 (a) 2.66 × 103 J (b) It will require more heat to increase the temperature of one mole of octane, C8H18(l), by a certain amount than to increase the temperature of one mole of water, H2O(l), by the same amount.
5.55 ΔH = –44.4 kJ/mol NaOH
5.57 ΔHrxn = –25.5 kJ/g C6H4O2 or –2.75 × 103 kJ/mol C6H4O2
5.59 (a) Heat capacity of the complete calorimeter = 14.4 kJ/°C (b) 7.56 °C
5.61 Hess's law is a consequence of the fact that enthalpy is a state function. Since ΔH is independent of path, we can describe a process by any series of steps that adds up to the overall process. ΔH for the process is the sum of ΔH values for the steps.
5.63 ΔH = –1300.0 kJ
5.65 ΔH = –2.49 × 103 kJ
5.67 (a) Standard conditions for enthalpy changes are P = 1 atm and some common temperature, usually 298 K. (b) Enthalpy of formation is the enthalpy change that occurs when a compound is formed from its component elements. (c) Standard enthalpy of formation ![]() is the enthalpy change that accompanies formation of one mole of a substance from elements in their standard states.
is the enthalpy change that accompanies formation of one mole of a substance from elements in their standard states.
5.69 (a) ![]() N2(g) + O2(g)
N2(g) + O2(g) ![]() NO2(g),
NO2(g), ![]() = 33.84 KJ (b) S(s) + 3/2 O2(g)
= 33.84 KJ (b) S(s) + 3/2 O2(g) ![]() SO3(g),
SO3(g), ![]() = –395.2 kJ (c) Na(s) +
= –395.2 kJ (c) Na(s) + ![]() (d) Pb(s) + N2(g) + 3 O2(g)
(d) Pb(s) + N2(g) + 3 O2(g) ![]() Pb(NO3)2(s),
Pb(NO3)2(s), ![]() = –451.9 kJ
= –451.9 kJ
5.71 ![]() = –847.6 kJ
= –847.6 kJ
5.73 (a) ![]() = –196.6 kJ (b)
= –196.6 kJ (b) ![]() = 37.1 kJ (c)
= 37.1 kJ (c) ![]() = –976.94 kJ (d)
= –976.94 kJ (d) ![]() = –68.3 kJ
= –68.3 kJ
5.75 ![]() = –248 kJ
= –248 kJ
5.77 (a) ![]() (b) 8 C(s, graphite) + 9 H2(g)
(b) 8 C(s, graphite) + 9 H2(g) ![]() C8H18(l) (c)
C8H18(l) (c) ![]() = –259.5 kJ
= –259.5 kJ
5.79 (a) C2H5OH(l) +3 O2(g) ![]() 2 CO2(g) + 3 H2O(g) (b)
2 CO2(g) + 3 H2O(g) (b) ![]() = –1234.8 kJ (c) 2.11 × 104 kJ/L heat produced (d) 0.071284 g CO2/kJ heat emitted
= –1234.8 kJ (c) 2.11 × 104 kJ/L heat produced (d) 0.071284 g CO2/kJ heat emitted
5.81 (a) Fuel value is the amount of energy produced when 1 g of a substance (fuel) is combusted. (b) 5 g of fat (c) These products of metabolism are expelled as waste via the alimentary tract, H2O(l) primarily in urine and feces, and CO2(g) as gas.
5.83 108 or 1 × 102 Cal/serving (b) Sodium does not contribute to the calorie content of the food because it is not metabolized by the body.
5.85 59.7 Cal
5.87 (a) ΔHcomb = –1850 kJ/mol C3H4, – 1926 kJ/mol C3H6, – 2044 kJ 4 mol C3H8 (b) ΔHcomb = –4.616 × 104 kJ/kg C3H4, –4.578 × 104 kJ/kg C3H6, –4.635 × 104 kJ/kg C3H8 (c) These three substances yield nearly identical quantities of heat per unit mass, but propane is marginally higher than the other two.
5.89 1 × 1012 kg C6H12O6/yr
5.91 (a) 469.4 m/s (b) 5.124 × 10–21 J (c) 3.086 kJ/mol
5.93 The spontaneous air bag reaction is probably exothermic, with –ΔH and thus –q. When the bag inflates, work is done by the system, so the sign of w is also negative.
5.97 ΔH = 38.95 kJ; ΔE = 36.48 kJ
5.102 (a) ![]() = –353.0 kJ (b) 1.2 g Mg needed
= –353.0 kJ (b) 1.2 g Mg needed
5.106 (a) ΔH° = –631.3 kJ (b) 3 mol of acetylene gas has greater enthalpy. (c) Fuel values are 50 kJ/g C2H2(g), 42 kJ/g C6H6(l).
5.109 If all work is used to increase the mans potential energy, the stair climbing uses 58 Cal and will not compensate for the extra order of 245 Cal fries. (More than 58 Cal will be required to climb the stairs because some energy is used to move limbs and some will be lost as heat.)
5.112 (a) 1.479 × 10–18 J/molecule (b) 1 × 10–15 J/photon. The X-ray has approximately 1000 times more energy than is produced by the combustion of 1 molecule of CH4(g).
5.114 (a) ΔH° for neutralization of the acids is HNO3, –55.8 kJ; HCl, –56.1 kJ; NH4+, –4.1 kJ. (b) H+(aq) + OH–(aq) ![]() H2O(l) is the net ionic equation for the first two reactions. NH4+(aq) + OH–(aq)
H2O(l) is the net ionic equation for the first two reactions. NH4+(aq) + OH–(aq) ![]() NH3(aq) + H2O(l) (c) The ΔH° values for the first two reactions are nearly identical, –55.8 kJ and –56.1 kJ. Since spectator ions do not change during a reaction and these two reactions have the same net ionic equation, it is not surprising that they have the same ΔH°. (d) Strong acids are more likely than weak acids to donate H+. Neutralization of the two strong acids is energetically favorable, while the third reaction is barely so. NH4+ is likely a weak acid.
NH3(aq) + H2O(l) (c) The ΔH° values for the first two reactions are nearly identical, –55.8 kJ and –56.1 kJ. Since spectator ions do not change during a reaction and these two reactions have the same net ionic equation, it is not surprising that they have the same ΔH°. (d) Strong acids are more likely than weak acids to donate H+. Neutralization of the two strong acids is energetically favorable, while the third reaction is barely so. NH4+ is likely a weak acid.
5.116 (a) ΔH° = –65.7 kJ (b) ΔH° for the complete molecular equation will be the same as ΔH° for the net ionic equation. Since the overall enthalpy change is the enthalpy of products minus the enthalpy of reactants, the contributions of spectator ions cancel. (c) ![]() for AgNO3(aq) is –100.4 kJ/mol.
for AgNO3(aq) is –100.4 kJ/mol.
CHAPTER 6
6.2 (a) 0.1 m or 10 cm (b) No. Visible radiation has wavelengths much shorter than 0.1 m. (c) Energy and wavelength are inversely proportional. Photons of the longer 0.1-m radiation have less energy than visible photons. (d) Radiation with λ = 0.1 m is in the low-energy portion of the microwave region. The appliance is probably a microwave oven.
6.5 (a) Increase (b) decrease (c) the light from the hydrogen discharge tube is a line spectrum, so not all visible wavelengths will be in our “hydrogen discharge rainbow.” Starting on the inside, the rainbow will be violet, then blue and blue-green. After a gap, the final band will be red.
6.8 (a) 1 (b) p (c) For the n = 4 shell, the lobes in the contour representation would extend farther along the y-axis.
6.11 (a) Meters (b) 1/second (c) meters/second
6.13 (a) True (b) False. Ultraviolet light has shorter wavelengths than visible light. (c) False. X-rays travel at the same speed as microwaves. (d) False. Electromagnetic radiation and sound waves travel at different speeds.
6.15 Wavelength of X-rays < ultraviolet < green light < red light < infrared < radio waves
6.17 (a) 3.0 × 1013 s–1 (b) 5.45 × 10–7 m = 545 nm (c) The radiation in (b) is visible; the radiation in (a) is not. (d) 1.50 × 104 m
6.19 5.64 × 1014 s–1; green.
6.21 Quantization means that energy changes can happen only in certain allowed increments. If the human growth quantum is one foot, growth occurs instantaneously in one-foot increments. The child experiences growth spurts of one foot; her height can change only by one-foot increments.
6.23 (a) 4.47 10,–21 J (b) 6.17 10–19 J (c) 69.2 nm
6.25 (a) λ = 3.3 μm, E = 6.0 × 10–20 J; λ = 0.154 nm, E = 1.29 × 10–15 J (b) The 3.3-μm photon is in the infrared region and the 0.154-nm photon is in the X-ray region; the X-ray photon has the greater energy.
6.27 (a) 6.11 × 10–19 J/photon (b) 368 kJ/mol (c) 1.64 × 1015 photons (d) 368 kJ/mol
6.29 (a) The ~ 1 × 10– 6 m radiation is in the infrared portion of the spectrum. (b) 8.1 × 1016photons/s
6.31 (a) Emin = 7.22 × 10–19 J (b) λ = 275 nm (c) E120 = 1.66 × 10–18 J. The excess energy of the 120-nm photon is converted into the kinetic energy of the emitted electron. Ek = 9.3 × 10–19 J/electron.
6.33 When applied to atoms, the notion of quantized energies means that only certain values of ΔE are allowed. These are represented by the lines in the emission spectra of excited atoms.
6.35 (a) Emitted (b) absorbed (c) emitted
6.37 (a) E2 = –5.45 × 10–19 J; E6 = –0.606 × 10–19 J; ΔE = 4.84 × 10–19 J; λ = 410 nm (b) visible, violet
6.39 (a) Only lines with nf = 2 represent ΔE values and wavelengths that lie in the visible portion of the spectrum. Lines with nf = 1 have shorter wavelengths and lines with nf > 2 have longer wavelengths than visible radiation. (b) ni = 3, nf = 2; λ = 6.56 × 10–7 m; this is the red line at 656 nmni = 4, nf = 2; λ = 4.86 × 10–7 m; this is the blue-green line at 486 nm. ni = 5, nf = 2; λ = 4.34 × 10–7 m; this is the blue-violet line at 434 nm.
6.41 (a) Ultraviolet region (b) ni 6, nf = 1
6.43 (a) λ = 5.6 × 10–37 m (b) λ = 2.65 × 10–34 m (c) λ = 2.3 × 10–13 m (d) λ = 1.51 × 10–11 m
6.45 4.14 × 103 m/s
6.47 (a) Δx ≥ 4 × 10–27 m (b) Δx ≥ 3 × 10–10 m
6.49 (a) The uncertainty principle states that there is a limit to how precisely we can simultaneously know the position and momentum (a quantity related to energy) of an electron. The Bohr model states that electrons move about the nucleus in precisely circular orbits of known radius and energy. This violates the uncertainty principle. (b) De Broglie stated that electrons demonstrate the properties of both particles and waves and that each moving particle has a wave associated with it. A wave function is the mathematical description of the matter wave of an electron. (c) Although we cannot predict the exact location of an electron in an allowed energy state, we can determine the probability of finding an electron at a particular position. This statistical knowledge of electron location is the probability density and is a function of Ψ2, the square of the wave function Ψ.
6.51 (a) n = 4, l = 3, 2, 1, 0 (b) l = 2, ml = –2, –1, 0, 1, 2 (c) ml = 2, l ≥ 2 or l = 2, 3 or 4
6.53 (a) 3p: n = 3, l = 1 (b) 2s: n = 2, l = 0 (c) 4f: n = 4, l = 3 (d) 5d: n = 5, l = 2
6.55 (a) impossible, 1p (b) possible (c) possible (d) impossible, 2d
6.57
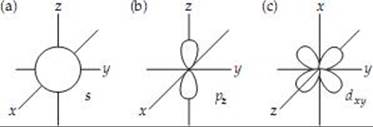
6.59 (a) The hydrogen atom 1s and 2s orbitals have the same overall spherical shape, but the 2s orbital has a larger radial extension and one more node than the 1s orbital. (b) A single 2p orbital is directional in that its electron density is concentrated along one of the three Cartesian axes of the atom. The dx2–y2 orbital has electron density along both the x- and y-axes, while the px orbital has density only along the x-axis. (c) The average distance of an electron from the nucleus in a 3s orbital is greater than for an electron in a 2s orbital. (d) 1s < 2p < 3d < 4f < 6s
6.61 (a) In the hydrogen atom, orbitals with the same principal quantum number, n, have the same energy. (b) In a many-electron atom, for a given n value, orbital energy increases with increasing l value: s < p < d < f.
6.63 (a) There are two main pieces of experimental evidence for electron “spin.” The Stern-Gerlach experiment shows that atoms with a single unpaired electron interact differently with an inhomogeneous magnetic field. Examination of the fine details of emission line spectra of multi-electron atoms reveals that each line is really a close pair of lines. Both observations can be rationalized if electrons have the property of spin.
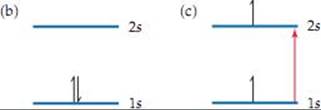
6.65 (a) 6 (b) 10 (c) 2 (d) 14
6.67 (a) “Valence electrons” are those involved in chemical bonding. They are part or all of the outer-shell electrons listed after the core. (b) “Core electrons” are inner-shell electrons that have the electron configuration of the nearest noble-gas element. (c) Each box represents an orbital. (d) Each half-arrow in an orbital diagram represents an electron. The direction of the half-arrow represents electron spin.
6.69 (a) Cs, [Xe]6s1 (b) Ni, [Ar]4s23d8 (c) Se, [Ar]4s23d104p4 (d) Cd, [Kr]5s24d10 (e) U, [Rn]5f 36d17s2 (f) Pb, [Xe]6s24f 145d106p2
6.71 (a) Be, 0 unpaired electrons (b) O, 2 unpaired electrons (c) Cr, 6 unpaired electrons (d) Te, 2 unpaired electrons
6.73 (a) The fifth electron would fill the 2p subshell before the 3s. (b) Either the core is [He], or the outer electron configuration should be 3s23p3. (c) The 3p subshell would fill before the 3d.
6.75 (a) λA = 3.6 × 10–8 m λB = 8.0 × 10–8 m (b) νA = 8.4 × 1015s–1 νB = 3.7 × 1015s–1 (c) A, ultraviolet; B, ultraviolet
6.78 66.7 min
6.82 1.6 × 107 photons/s, 5.1 × 10–12 J/s
6.85 (a) The Paschen series lies in the infrared. (b) ni = 4, λ = 1.87 × 10– 6 m; ni = 5, λ = 1.28 × 10– 6 m; ni = 6, λ = 1.09 × 10– 6 m
6.90 (a) l (b) n and l (c) ms (d) ml
6.92 (a) The nodal plane of the pz orbital is the xy-plane. (b) The two nodal planes of the dxy orbital are the ones where x = 0 and y = 0. These are the yz- and xz-planes. (c) The two nodal planes of the dx2–y2 orbital are the ones that bisect the x- and y-axes and contain the z-axis.
6.94 If ms had three allowed values instead of two, each orbital would hold three electrons instead of two. Assuming that there is no change in the n, l, and ml values, the number of elements in each of the first four rows would be 1st row, 3 elements; 2nd row, 12 elements; 3rd row, 12 elements; 4th row, 27 elements
6.97 (a) 1.7 × 1028 photons (b) 34 s
6.101 (a) Bohr's theory was based on the Rutherford nuclear model of the atom: a dense positive charge at the center and a diffuse negative charge surrounding it. Bohr's theory then specified the nature of the diffuse negative charge. The prevailing theory before the nuclear model was Thomson's plum pudding model: discrete electrons scattered about a diffuse positive charge cloud. Bohr's theory could not have been based on the Thomson model of the atom. (b) De Broglie's hypothesis is that electrons exhibit both particle and wave properties. Thomson's conclusion that electrons have mass is a particle property, while the nature of cathode rays is a wave property. De Broglie's hypothesis actually rationalizes these two seemingly contradictory observations about the properties of electrons.
CHAPTER 7
7.3 (a) The bonding atomic radius of A, rA, is d1/2; rx = d2 – (d/2). (b) The length of the X — X bond is 2rx or 2d2 – d1.
7.6 (a) X + 2F2![]() XF4 (b) X in the diagram has about the same bonding radius as F, so it is likely to be a nonmetal.
XF4 (b) X in the diagram has about the same bonding radius as F, so it is likely to be a nonmetal.
7.7 The number of columns in the various blocks of the periodic chart corresponds to the maximum number of electrons that can occupy the various kinds of atomic orbitals: 2 columns on the left for 2 electrons in s orbitals, 10 columns in the transition metals for 10 electrons in d orbitals, 6 columns on the right for 6 electrons in p orbitals, 14-member rows below for 14 electrons in f orbitals. The order of blocks corresponds to the filling order of atomic orbitals, and the row number corresponds to the principal quantum number of the valence electrons of elements in that row, ns,np, (n – 1)d, (n – 2)f.
7.9 In general, elements are discovered according to their ease of isolation in elemental form.
7.11 (a) Effective nuclear charge, Zeff, is a representation of the average electrical field experienced by a single electron. It is the average environment created by the nucleus and the other electrons in the molecule, expressed as a net positive charge at the nucleus. (b) Going from left to right across a period, effective nuclear charge increases.
7.13 (a) For both Na and K, Zeff = 1. (b) For both Na and K, Zeff = 2.2. (c) Slater's rules give values closer to the detailed calculations: Na, 2.51; K, 3.49. (d) Both approximations give the same value of Zeff for Na and K; neither accounts for the gradual increase in Zeff moving down a group. (e) Following the trend from detailed calculations, we predict a Zeff value of approximately 4.5.
7.15 The n = 3 electrons in Kr experience a greater effective nuclear charge and thus have a greater probability of being closer to the nucleus.
7.17 (a) Atomic radii are determined by measuring distances between atoms in various situations. (b) Bonding radii are calculated from the internuclear separation of two atoms joined by a covalent chemical bond. Nonbonding radii are calculated from the internuclear separation between two gaseous atoms that collide and move apart but do not bond. (c) For a given element, the nonbonding radius is always larger than the bonding radius. (d) If a free atom reacts to become part of a covalent molecule, its radius changes from nonbonding to bonding and the atom gets smaller.
7.19 (a) 1.37 Å (b) The distance between W atoms will decrease.
7.21 From the sum of the atomic radii, As — I = 2.52 Å. This is very close to the experimental value of 2.55 Å.
7.23 (a) Decrease (b) increase (c) O < Si < Ge < I
7.25 (a) Cs > K > Li (b) Pb > Sn > Si (c) N > O > F
7.27 (a) False (b) true (c) false
7.29 The red sphere is a metal; its size decreases on reaction, characteristic of the change in radius when a metal atom forms a cation. The blue sphere is a nonmetal; its size increases on reaction, characteristic of the change in radius when a nonmetal atom forms an anion.
7.31 (a) An isoelectronic series is a group of atoms or ions that have the same number of electrons and the same electron configuration. (b) Ga3+ : Ar; Zr4+ : Kr; Mn7+ : Ar; I–: Xe; Pb2+: Hg
7.33 (a) Ar (b) Ar (c) There is no neutral atom isoelectronic with Fe2+. Because transition metals fill the s subshell first but also lose s electrons first when they form ions, many transition metal ions do not have isolectronic neutral atoms. (d) No isoelectronic neutral atom; same reason as part (c). (e) No isoelectronic neutral atom; same reason as part (c).
7.35 (a) K+ is smaller. (b) Cl–, Zeff = 7; K+, Zeff = 9 (c) Cl–: Zeff = 5.75; K+, Zeff = 7.75 (d) For isoelectronic ions, as nuclear charge (Z) increases, effective nuclear charge (Zeff) increases and ionic radius decreases.
7.37 (a) Se < Se2– < Te2– (b) Co3+ < Fe3+< Fe2+ (c) Ti4+ < Sc3+ < Ca (d) Be2+ < Na+ < Ne
7.39 Al(g) ![]() Al+(g) + le–; Al+(g)
Al+(g) + le–; Al+(g) ![]() Al2+(g) + le–; Al2–(g)
Al2+(g) + le–; Al2–(g) ![]() Al3+ (g) + le–. The process for the first ionization energy requires the least amount of energy.
Al3+ (g) + le–. The process for the first ionization energy requires the least amount of energy.
7.41 (a) False. Ionization energies are always positive quantities. (b) False. F has a greater first ionization energy than O. (c) True.
7.43 (a) The smaller the atom, the larger its first ionization energy. (b) Of the nonradioactive elements, He has the largest and Cs the smallest first ionization energy.
7.45 (a) Cl (b) Ca (c) K (d) Ge (e) Sn
7.47 (a) Fe2+, [Ar]3d6 (b) Hg2+, [Xe]4f145d10 (c) Mn2+, [Ar]3d5 (d) Pt2+, [Xe]4f145d8 (e) P3–, [Ne]3s23p6
7.49 Ni2+, [Ar]3d8; Pd2+, [Kr]4d8; Pt2+, [Xe]4f145d8
7.51 (a) Positive, endothermic, values for ionization energy and electron affinity mean that energy is required to either remove or add electrons. Valence electrons in Ar experience the largest Zeff of any element in the third row, resulting in a large, positive ionization energy. When an electron is added to Ar, the n = 3 electrons become core electrons that screen the extra electron so effectively that Ar– has a higher energy than an Ar atom and a free electron. This results in a large positive electron affinity. (b) kJ/mol
7.53 Electron affinity of Br: Br(g) + le–![]() Br–(g); [Ar]4s23d104p5
Br–(g); [Ar]4s23d104p5![]() [Ar]4s23d104p6; electron affinity of Kr: Kr(g) + 1 e–
[Ar]4s23d104p6; electron affinity of Kr: Kr(g) + 1 e–![]() Kr–(g); [Ar]4s23d104p6
Kr–(g); [Ar]4s23d104p6![]() [Ar]4s23d104p65s1. Br– adopts the stable electron configuration of Kr; the added electron experiences essentially the same Zeff and stabilization as the other valence electrons and electron affinity is negative. In Kr– ion, the added electron occupies the higher energy 5s orbital. A 5s electron is farther from the nucleus, effectively shielded by the spherical Kr core and not stabilized by the nucleus; electron affinity is positive.
[Ar]4s23d104p65s1. Br– adopts the stable electron configuration of Kr; the added electron experiences essentially the same Zeff and stabilization as the other valence electrons and electron affinity is negative. In Kr– ion, the added electron occupies the higher energy 5s orbital. A 5s electron is farther from the nucleus, effectively shielded by the spherical Kr core and not stabilized by the nucleus; electron affinity is positive.
7.55 (a) Ionization energy (I1) of Ne: Ne(g) ![]() Ne (g) + 1 e– ; [He]2s22p6
Ne (g) + 1 e– ; [He]2s22p6![]() [He]2s22p5; electron affinity (E1) of F: F(g) + 1 e–
[He]2s22p5; electron affinity (E1) of F: F(g) + 1 e–![]() F–(g); [He]2s22 p 5
F–(g); [He]2s22 p 5![]() [He]2s22p 6. (b) I1 of Ne is positive; E1 of F is negative. (c) One process is apparently the reverse of the other, with one important difference. Ne has a greater Z and Zeff, so we expect I1 for Ne to be somewhat greater in magnitude and opposite in sign to E1 for F.
[He]2s22p 6. (b) I1 of Ne is positive; E1 of F is negative. (c) One process is apparently the reverse of the other, with one important difference. Ne has a greater Z and Zeff, so we expect I1 for Ne to be somewhat greater in magnitude and opposite in sign to E1 for F.
7.57 The smaller the first ionization energy of an element, the greater the metallic character of that element.
7.59 Agree. When forming ions, all metals form cations. The only nonmetallic element that forms cations is the metalloid Sb, which is likely to have significant metallic character.
7.61 Ionic: SnO2, Al2O3, Li2O, Fe2O3; molecular: CO2, H2O. Ionic compounds are formed by combining a metal and a nonmetal; molecular compounds are formed by two or more nonmetals.
7.63 (a) An acidic oxide dissolved in water produces an acidic solution; a basic oxide dissolved in water produces a basic solution. (b) Oxides of nonmetals, such as SO3, are acidic; oxides of metals, such as CaO, are basic.
7.65 (a) Dichlorineheptoxide (b) 2 Cl2(g) + 7 O2(g) ![]() 2 Cl2O7(l) (c) While most nonmetal oxides we have seen, such as CO2 or SO2, are gases, a boiling point of 81 °C is expected for a large molecule like Cl2O7. (d) Cl2O7 is an acidic oxide, so it will be more reactive to base, OH–. (e) The oxidation state of Cl in Cl2O7 is +7; the corresponding electron configuration for Cl is [He]2s2p6 or [Ne].
2 Cl2O7(l) (c) While most nonmetal oxides we have seen, such as CO2 or SO2, are gases, a boiling point of 81 °C is expected for a large molecule like Cl2O7. (d) Cl2O7 is an acidic oxide, so it will be more reactive to base, OH–. (e) The oxidation state of Cl in Cl2O7 is +7; the corresponding electron configuration for Cl is [He]2s2p6 or [Ne].
7.67 (a) BaO(s) + H2O(l) ![]() Ba(OH)2(aq) (b) FeO(s) + 2 HClO4(aq)
Ba(OH)2(aq) (b) FeO(s) + 2 HClO4(aq) ![]() Fe(ClO4)2(aq) +H2O(l) (c) SO3(g) + H2O(l)
Fe(ClO4)2(aq) +H2O(l) (c) SO3(g) + H2O(l) ![]() H2SO4(aq) (d) CO2(g) + 2 NaOH(aq)
H2SO4(aq) (d) CO2(g) + 2 NaOH(aq) ![]() Na2CO3(aq) + H2O(l)
Na2CO3(aq) + H2O(l)
7.69 Yes, the reactivity of a metal correlates with its first ionization energy. Since metals lose electrons when they form ions, the less energy required for this process, the more reactive the metal. However, we usually observe reactivity of metals in the solid state and ionization energy is a gas phase property, so there are differences between the two properties.
7.71 (a) Ca is more reactive because it has a lower ionization energy than Mg. (b) K is more reactive because it has a lower ionization energy than Ca.
7.73 (a) 2 K(s) + Cl2(g) ![]() 2 KCl(s) (b) SrO(s) + H2O(l)
2 KCl(s) (b) SrO(s) + H2O(l) ![]() Sr(OH)2(aq) (c) 4 Li(s) + O2(g)
Sr(OH)2(aq) (c) 4 Li(s) + O2(g) ![]() 2 Li2O(s) (d) 2 Na(s) + S(l)
2 Li2O(s) (d) 2 Na(s) + S(l) ![]() Na2S(s)
Na2S(s)
7.75 (a) Both classes of reaction are redox reactions where either hydrogen or the halogen gains electrons and is reduced. The product is an ionic solid, where either hydride ion, H– or a halide ion, X–, is the anion. (b) Ca(s) + F2(g) ![]() CaF2(s); Ca(s) + H2(g)
CaF2(s); Ca(s) + H2(g) ![]() CaH2(s). Both products are ionic solids containing Ca2+ and the corresponding anion in a 1:2 ratio.
CaH2(s). Both products are ionic solids containing Ca2+ and the corresponding anion in a 1:2 ratio.
7.77 (a) Br, [Ar]4s24p5; Cl, [Ne]3s23p5 (b) Br and Cl are in the same group, and both adopt a 1 – ionic charge. (c) The ionization energy of Br is smaller than that of Cl, because the 4p valence electrons in Br are farther from to the nucleus and less tightly held than the 3p electrons of Cl. (d) Both react slowly with water to form HX + HOX (e) The electron affinity of Br is less negative than that of Cl, because the electron added to the 4p orbital in Br is farther from the nucleus and less tightly held than the electron added to the 3p orbital of Cl. (f) The atomic radius of Br is larger than that of Cl, because the 4p valence electrons in Br are farther from the nucleus and less tightly held than the 3p electrons of Cl.
7.79 (a) The term inert was dropped because it no longer described all the Group 8A elements. (b) In the 1960s, scientists discovered that Xe would react with substances having a strong tendency to remove electrons, such as F2. Thus, Xe could not be categorized as an “inert” gas. (c) The group is now called the noble gases.
7.81 (a) 2 O3(g) ![]() 3 O2(g) (b) Xe(g) + F2(g)
3 O2(g) (b) Xe(g) + F2(g) ![]() XeF2(g); Xe(g) + 2 F2(g)
XeF2(g); Xe(g) + 2 F2(g) ![]() XeF4(s); Xe(g) + 3 F2(g)
XeF4(s); Xe(g) + 3 F2(g) ![]() XeF6(s) (c) S(s) + (d) 2 F2(g) + 2 H2O(l)
XeF6(s) (c) S(s) + (d) 2 F2(g) + 2 H2O(l) ![]() 4 HF(aq) + O2(g)
4 HF(aq) + O2(g)
7.83 Up to Z = 82, there are three instances where atomic weights are reversed relative to atomic numbers: Ar and K; Co and Ni; Te and I. In each case the most abundant isotope of the element with the larger atomic number has one more proton but fewer neutrons than the element with the smaller atomic number. The smaller number of neutrons causes the element with the larger Z to have a smaller than expected atomic weight.
7.85 (a) 5+ (b) 4.8+ (c) Shielding is greater for 3p electrons, owing to penetration by 3s electrons, so Zeff for 3p electrons is less than that for 3s electrons. (d) The first electron lost is a 3p electron because it has a smaller Zeff and experiences less attraction for the nucleus than a 3s electron does.
7.88 (a) The estimated distances are a bit longer than the measured distances. This probably shows a systematic bias in either the estimated radii or in the method of obtaining the measured values. (b) The principal quantum number of the outer electrons and thus the average distance of these electrons from the nucleus increase from P(n = 3) to As(n = 4) to Sb(n = 5). This causes the systematic increase in M – H distance.
7.92 (a) 2Sr(s) + O2(g) ![]() 2SrO(s) (b) Based on ionic radii, the length of the side of the cube is 5.16 Å. (c) There are four SrO units in the cube.
2SrO(s) (b) Based on ionic radii, the length of the side of the cube is 5.16 Å. (c) There are four SrO units in the cube.
7.95
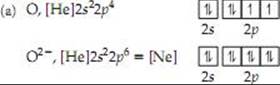
(b) O3–, [Ne]3s1. The third electron would be added to the 3s orbital, which is farther from the nucleus and more strongly shielded by the [Ne] core. The overall attraction of this 3s electron for the oxygen nucleus is not large enough for O3– to be a stable particle.
7.98 (a) For both H and the alkali metals, the added electron will complete an ns subshell, so shielding and repulsion effects will be similar. For the halogens, the electron is added to an np subshell, so the energy change is likely to be quite different. (b) True. The electron configuration of H is 1s1. The single 1s electron experiences no repulsion from other electrons and feels the full unshielded nuclear charge. The outer electrons of all other elements that form compounds are shielded by a spherical inner core of electrons and are less strongly attracted to the nucleus, resulting in larger bonding atomic radii. (c) Both H and the halogens have large ionization energies. The relatively large effective nuclear charge experienced by np electrons of the halogens is similar to the unshielded nuclear charge experienced by the H 1s electron. For the alkali metals, the ns electron being removed is effectively shielded by the core electrons, so ionization energies are low. (d) ionization energy of hydride, H–(g) ![]() H(g) + 1 e– (e) electron affinity of hydrogen, H(g) + 1 e–
H(g) + 1 e– (e) electron affinity of hydrogen, H(g) + 1 e–![]() H–(g). The value for the ionization energy of hydride is equal in magnitude but opposite in sign to the electron affinity of hydrogen.
H–(g). The value for the ionization energy of hydride is equal in magnitude but opposite in sign to the electron affinity of hydrogen.
7.103 Electron configuration [Rn]7s25f 146d107p5; first ionization energy, 805 kJ/mol; electron affinity, –235 kJ/mol; atomic size, 1.65 Å; common oxidation state, –1
7.106 (a) Li, [He]2s1; Zeff ≈ 1+ (b) I1 ≈ 5.45 X 10–19 J/mol ≈ 328 kJ/mol (c) The estimated value of 328 kJ/mol is less than the Table 7.4 value of 520 kJ/mol. Our estimate for Zeff was a lower limit; the [He] core electrons do not perfectly shield the 2s electron from the nuclear charge. (d) Based on the experimental ionization energy, Zeff = 1.26. This value is greater than the estimate from part (a) but agrees well with the “Slater” value of 1.3 and is consistent with the explanation in part (c).
7.108 (a) 9.8902 Å. (b) For Hg, the first ionization energy is 1007 kJ/mol, while the XPS energy of the 4f electron is 10,100 kJ/mol. The energy required to remove a 4f core electron is 10 times the energy required to remove a 6s valence electron. For O, the first ionization energy is 1314 kJ/mol, while the XPS energy of a 1s electron is 51,200 kJ/mol. The energy required to remove a 1s core electron is 40 times that required to remove a 2p valence electron. (c) Hg2+, [Xe]4 f 145d10; valence electrons are 5d. O2–, [He]2s22p6 or [Ne]; valence electrons are 2p (d) Hg2+5d, Zeff = 18.85; Hg2+4f, Zeff = 43.85; O2–4f, Zeff = 3.85.
7.110 (a) Mg3N2 (b) Mg3N2(s) + 3 H2O(l) ![]() 3 MgO(s) + 2 NH3(g); the driving force is the production of NH3(g). (c) 17% Mg3N2 (d) 3 Mg(s) + 2 NH3(g)
3 MgO(s) + 2 NH3(g); the driving force is the production of NH3(g). (c) 17% Mg3N2 (d) 3 Mg(s) + 2 NH3(g) ![]() Mg3N2(s) + 3 H2(g). NH3 is the limiting reactant and 0.46 g H2 is formed. (e) ΔH°rxn = – 368.70 kJ
Mg3N2(s) + 3 H2(g). NH3 is the limiting reactant and 0.46 g H2 is formed. (e) ΔH°rxn = – 368.70 kJ
CHAPTER 8
8.1 (a) Group 4A or 14 (b) Group 2A or 2 (c) Group 5A or 15
8.4 (a) Ru (b) [Kr]5s24d6.
8.7 (a) Moving from left to right along the molecule, the first C needs 2 H atoms, the second needs 1, the third needs none, and the fourth needs 1. (b) In order of increasing bond length: 3 < 1 < 2 (c) In order of increasing bond enthalpy: 2 < 1 < 3
8.9 (a) Valence electrons are those that take part in chemical bonding. This usually means the electrons beyond the core noble-gas configuration of the atom, although it is sometimes only the outer-shell electrons. (b) A nitrogen atom has 5 valence electrons. (c) The atom (Si) has 4 valence electrons.
8.11 Si, 1s22s22p63s23p2. The n = 3 electrons are valence electrons; the others are nonvalence electrons. Valence electrons participate in chemical bonding; the others do not.
8.13
![]()
8.15
![]()
8.17 (a) AlF3 (b) K2S (c) Y2O3 (d) Mg3N2
8.19 (a) Sr2+, [Ar]4s23d104p6 = [Kr], noble-gas configuration (b) Ti2+, [Ar]3d2 (c) Se2–, [Ar]4s23d104p6 = [Kr], noble-gas configuration (d) Ni2+, [Ar]3d8 (e) Br–, [Ar]4s23d104p6 = [Kr], noble-gas configuration (f) Mn3+, [Ar]3d4
8.21 (a) Lattice energy is the energy required to totally separate one mole of solid ionic compound into its gaseous ions. (b) The magnitude of the lattice energy depends on the magnitudes of the charges of the two ions, their radii, and the arrangement of ions in the lattice.
8.23 KF, 808 kJ/mol; CaO, 3414 kJ/mol; ScN, 7547 kJ/mol. The interionic distances in the three compounds are similar. For compounds with similar ionic separations, the lattice energies should be related as the product of the charges of the ions. The lattice energies above are approximately related as 1 : 4 : 9. Slight variations are due to the small differences in ionic separations.
8.25 Since the ionic charges are the same in the two compounds, the K — Br and Cs — Cl separations must be approximately equal.
8.27 The large attractive energy between oppositely charged Ca2+and O2– more than compensates for the energy required to form Ca2+ and O2– from the neutral atoms.
8.29 The lattice energy of RbCl(s) is +692 kJ/mol. This value is smaller than the lattice energy for NaCl because Rb has a larger ionic radius than Na and therefore cannot approach Cl– as closely as Na+ can.
8.31 (a) A covalent bond is the bond formed when two atoms share one or more pairs of electrons. (b) Any simple compound whose component atoms are nonmetals, such as H2, SO2, and CCl4, are molecular and have covalent bonds between atoms. (c) Covalent, because it is a gas at room temperature and below.
8.33
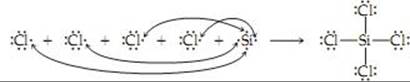
8.35 (a) ![]() (b) A double bond is required because there are not enough electrons to satisfy the octet rule with single bonds and unshared pairs. (c) The greater the number of shared electron pairs between two atoms, the shorter the distance between the atoms. An O Ⅸ O double bond is shorter than an O — O single bond.
(b) A double bond is required because there are not enough electrons to satisfy the octet rule with single bonds and unshared pairs. (c) The greater the number of shared electron pairs between two atoms, the shorter the distance between the atoms. An O Ⅸ O double bond is shorter than an O — O single bond.
8.37 (a) Electronegativity is the ability of an atom in a molecule to attract electrons to itself. (b) The range of electronegativities on the Pauling scale is 0.7-4.0. (c) Fluorine is the most electronegative element. (d) Cesium is the least electronegative element that is not radioactive.
8.39 (a) Mg (b) S (c) C (d) As
8.41 The bonds in (a), (c), and (d) are polar. The more electronegative element in each polar bond is (a) F (c) O (d) I.
8.43 (a) The calculated charge on H and Br is 0.12e. (b) From Sample Exercise 8.5, the calculated charge on H and Cl in HCl is 0.178e. HBr has a smaller dipole moment and longer bond length than HCl; these properties both contribute to the smaller charge separation in HBr.
8.45 (a) SiCl4, molecular, silicon tetrachloride; LaF3, ionic, lanthanum(III) fluoride (b) FeCl2, ionic, iron(II) chloride; ReCl6, molecular (metal in high oxidation state), rhenium hexachloride. (c) PbCl4, molecular (by contrast to the distinctly ionic RbCl), lead tetrachloride; RbCl, ionic, rubidium chloride
8.47
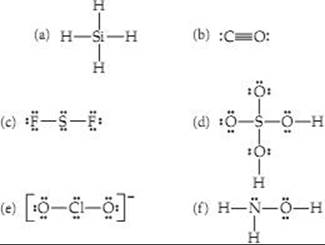
8.49 (a) Formal charge is the charge on each atom in a molecule, assuming all atoms have the same electronegativity. (b) Formal charges are not actual charges. They are a bookkeeping system that assumes perfect covalency, one extreme for the possible electron distribution in a molecule. (c) Oxidation numbers are a bookkeeping system that assumes the more electronegative element holds all electrons in a bond. The true electron distribution is some composite of the two extremes.
8.51 Formal charges are shown on the Lewis structures; oxidation numbers are listed below each structure.
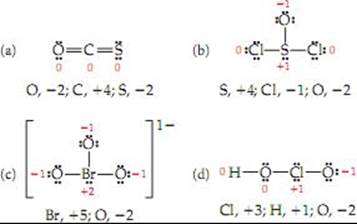
8.53
![]()
(b) O3 is isoelectronic with NO2–; both have 18 valence electrons. (c) Since each N — O bond has partial double-bond character, the N — O bond length in NO2– should be shorter than an N — O single bond.
8.55 The more electron pairs shared by two atoms, the shorter the bond. Thus, the C — O bond lengths vary in the order CO < CO2 < CO32–.
8.57 (a) Two equally valid Lewis structures can be drawn for benzene.
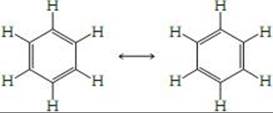
The concept of resonance dictates that the true description of bonding is some hybrid or blend of these two Lewis structures. The most obvious blend of these two resonance structures is a molecule with six equivalent C — C bonds with equal lengths. (b) This model predicts a uniform C — C bond length that is shorter than a single bond but longer than a double bond.
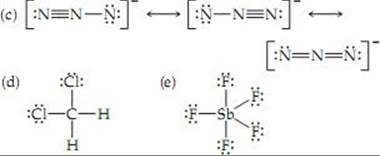
8.59 (a) The octet rule states that atoms will gain, lose, or share electrons until they are surrounded by eight valence electrons. (b) The octet rule applies to atoms in a covalent compound and the individual ions in an ionic compound. In the covalent compound CCl4, the atoms share electrons in order to surround themselves with an octet. In the ionic compound MgCl2, Mg loses 2 e– to become Mg2+ with the electron configuration of Ne. Each Cl– atom gains one electron to form Cr– with the electron configuration of Ar.
8.61 No chlorine oxide will obey the octet rule. Chlorine has seven valence electrons, and oxygen has six. For neutral chlorine oxides, regardless of the number of oxygen atoms in the molecule, the total number of valence electrons will be an (odd + even) sum, which is always an odd number.
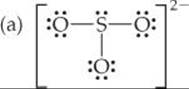
8.63
Other resonance structures that minimize formal charges but violate the octet rule can be drawn. The octet rule versus formal charge debate is ongoing.
![]()
6 electrons around Al
10 electrons around Sb
8.65
![]()
This structure violates the octet rule.
![]()
(c) Formal charges are minimized on the structure that violates the octet rule; this form is probably dominant.
8.67 Three resonance structures for HSO3– are shown here. Because the ion has a 1– charge, the sum of the formal charges of the atoms is –1.
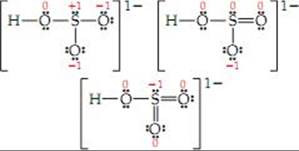
The structure with no double bonds obeys the octet rule for all atoms, but does not lead to minimized formal charges. The structures with one and two double bonds both minimize formal charge but do not obey the octet rule. Of these two, the structure with one double bond is preferred because the formal charge is localized on the more electronegative oxygen atom.
8.69 (a) ΔH = –304 kJ (b) ΔH = –82 kJ (c) ΔH = –467 kJ
8.71 (a) ΔH = –321 kJ (b) ΔH = –103 kJ (c) ΔH = –203 kJ
8.73 (a) –97 kJ; exothermic (b) The ΔH calculated from bond enthalpies (–97 kJ) is slightly more exothermic (more negative) than that obtained using ΔH°f values (–92.38 kJ).
8.75 The average Ti—Cl bond enthalpy is 430 kJ/mol.
8.77 (a) Six (nonradioactive) elements. Yes, they are in the same family, assuming H is placed with the alkali metals. The Lewis symbol represents the number of valence electrons of an element, and all elements in the same family have the same number of valence electrons. By definition of a family, all elements with the same Lewis symbol must be in the same family.
8.81 The charge on M is likely to be 3+. The range of lattice energies for ionic compounds with the general formula MX and a charge of 2+ on the metal is 3–4 × 103 kJ/mol. The lattice energy of 6 × 103 kJ/mol indicates that the charge on M must be greater than 2+.
8.85 (a) B — O. The most polar bond will be formed by the two elements with the greatest difference in electronegativity. (b) Te — I. These elements have the two largest covalent radii among this group. (c) TeI2. The octet rule is be satisfied for all three atoms. (d) P2O3. Each P atom needs to share 3 e – and each O atom 2e– to achieve an octet. And B2O3. Although this is not a purely ionic compound, it can be understood in terms of gaining and losing electrons to achieve a noble-gas configuration. If each B atom were to lose 3 e – and each O atom were to gain 2e–, charge balance and the octet rule would be satisfied.
8.90 (a) +1 (b) –1 (c) +1 (assuming the odd electron is on N) (d) 0 (e) +3
8.95 An experimentally determined molecular structure will reveal bond lengths and angles of the B — A = B molecule. If resonance structures are important, the two B — A bond lengths will be identical. If the molecule features one single and one double bond, the lengths will be significantly different.
8.98 (a) ΔH = 7.85 kJ/g nitroglycerine (b) 4C7H5N3O6(s) ![]() 6N2(g) + 7CO2(g) + 10H2O(g) + 21C(s)
6N2(g) + 7CO2(g) + 10H2O(g) + 21C(s)
8.101 (a) Ti2+, [Ar]3d2; Ca, [Ar]4s2. Yes. The 2 valence electrons in Ti2+ and Ca are in different principal quantum levels and different subshells. (b) In Ca the 4s is lower in energy than the 3d, while in Ti2+ the 3d is lower in energy than the 4s. (c) No. There is only one 4s orbital, so the 2 valence electrons in Ca are paired; there are 5 degenerate 3d orbitals, so the 2 valence electrons in Ti2+ are unpaired.
8.107 (a) Azide ion is N3–. (b) Resonance structures with formal charges are shown.
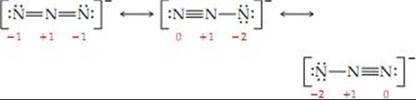
(c) The structure with two double bonds minimizes formal charges and is probably the main contributor. (d) The N — N distances will be equal and have the approximate length of a N — N double bond, 1.24 Å.
8.112 (a) D(Br — Br)(l) = 223.6 kJ; D(Br — Br)(g) = 193 kJ (b) D(C — Cl)(l) = 336.1 kJ; D(C — Cl)(g) = 328kJ (c) D(O — O)(l) = 192.7kJ; D(O — O)(g) = 146kJ (d) Breaking bonds in the liquid requires more energy than breaking bonds in the gas phase. Bond dissociation in the liquid phase can be thought of in two steps, vaporization of the liquid followed by bond dissociation in the gas phase. The greater bond dissociation enthalpy in the liquid phase is due to the contribution from the enthalpy of vaporization.
CHAPTER 9
9.1 Removing an atom from the equatorial plane of the trigonal bipyra-mid in Figure 9.3 creates a seesaw shape.
9.3 (a) 2 electron-domain geometries, linear and trigonal bipyramidal (b) 1 electron-domain geometry, trigonal bipyramidal (c) 1 electron-domain geometry, octahedral (c) 1 electron-domain geometry, octahedral (d) 1 electron domain geometry, octahedral (e) 1 electron domain geometry, octahedral (f) 1 electron-domain geometry, trigonal bipyramidal (This triangular pyramid is an unusual molecular geometry not listed in Table 9.3. It could occur if the equatorial substituents on the trigonal bipyramid were extremely bulky, causing the nonbonding electron pair to occupy an axial position.)
9.5 (a) Zero energy corresponds to two separate, noninteracting Cl atoms. This infinite Cl — Cl distance is beyond the right extreme of the horizontal axis on the diagram. (b) According to the valence bond model, valence orbitals on the approaching atoms overlap, allowing two electrons to mutually occupy space between the two nuclei and be stabilized by two nuclei rather than one. (c) The Cl — Cl distance at the energy minimum on the plot is the Cl — Cl bond length. (d) At interatomic separations shorter than the bond distance, the two nuclei begin to repel each other, increasing the overall energy of the system. (e) The y-coordinate of the minimum point on the plot is a good estimate of the Cl — Cl bond energy or bond strength.
9.6 SiCl4, 109°; PF3, 107°; SF2, 105°. Each molecule has tetrahedral electron domain geometry, but the number of nonbonding electron pairs increases from 0 to 2, respectively. Because nonbonding electron pairs occupy more space than bonding pairs, we expect the bond angles to decrease in the series.
9.9 (a) i, Two s atomic orbitals; ii, two p atomic orbitals overlapping end to end; iii, two p atomic orbitals overlapping side to side (b) i, σ-type MO; ii, σ-type MO; iii, π-type MO (c) i, antibonding; ii, bonding; iii, antibonding (d) i, the nodal plane is between the atom centers, perpendicular to the interatomic axis and equidistant from each atom. ii, there are two nodal planes; both are perpendicular to the interatomic axis. One is left of the left atom and the second is right of the right atom. iii, there are two nodal planes; one is between the atom centers, perpendicular to the interatomic axis and equidistant from each atom. The second contains the interatomic axis and is perpendicular to the first.
9.11 (a) Yes. The stated shape defines the bond angle and the bond length tells the size. (b) No. Atom A could have 2, 3, or 4 nonbonding electron pairs.
9.13 A molecule with tetrahedral molecular geometry has an atom at each vertex of the tetrahedron. A trigonal-pyramidal molecule has one vertex of the tetrahedron occupied by a nonbonding electron pair rather than an atom.
9.15 (a) An electron domain is a region in a molecule where electrons are most likely to be found. (b) Like the balloons in Figure 9.5, each electron domain occupies a finite volume of space, so they also adopt an arrangement where repulsions are minimized.
9.17 (a) The number of electron domains in a molecule or ion is the number of bonds (double and triple bonds count as one domain) plus the number of non-bonding electron pairs. (b) A bonding electron domain is a region between two bonded atoms that contains one or more pairs of bonding electrons. A nonbonding electron domain is localized on a single atom and contains one pair of nonbonding electrons.
9.19 (a) No effect on molecular shape (b) 1 nonbonding pair on P influences molecular shape (c) no effect (d) no effect (e) 1 nonbonding pair on S influences molecular shape
9.21 (a) 2 (b) 1 (c) none (d) 3
9.23 The electron-domain geometry indicated by VSEPR describes the arrangement of all bonding and nonbonding electron domains. The molecular geometry describes just the atomic positions. In H2O there are 4 electron domains around oxygen, so the electron-domain geometry is tetrahedral. Because there are 2 bonding and 2 nonbonding domains, the molecular geometry is bent. We make this distinction because all electron domains must be considered when describing the atomic arrangement and bond angles in a molecule but the molecular geometry or shape is a description of just the atom positions.
9.25 (a) Tetrahedral, tetrahe-dral (b) trigonal bipyramidal, T-shaped (c) octahedral, square pyramidal (d) octahedral, square planar
9.27 (a) Linear, linear (b) tetrahedral, trigonal pyramidal (c) trigonal bipyramidal, seesaw (d) octahedral, octahedral (e) tetrahedral, tetrahedral (f) linear, linear
9.29 (a) i, trigonal planar; ii, tetrahedral; iii, trigonal bipyramidal (b) i, 0; ii, 1; iii, 2 (c) N and P (d) Cl (or Br or I). This T-shaped molecular geometry arises from a trigonal-bipyramidal electron-domain geometry with 2 nonbonding domains. Assuming each F atom has 3 non-bonding domains and forms only single bonds with A, A must have 7 valence electrons and be in or below the third row of the periodic table to produce these electron-domain and molecular geometries.
9.31 (a) 1 – 109°, 2 – 109° (b) 3 – 109°, 4 – 109° (c) 5 – 180° (d) 6 – 120°, 7 – 109°, 8 – 109°
9.33 The two molecules with trigonal-bipyramidal electron-domain geometry, PF5 and SF4, have more than one F — A — F bond angle.
9.35 (a) Although both ions have 4 bonding electron domains, the 6 total domains around Br require octahedral domain geometry and square-planar molecular geometry, while the 4 total domains about B lead to tetrahedral domain and molecular geometry. (b) The less electronegative the central atom, the larger the non-bonding electron domain, and the greater the effect of repulsive forces on adjacent bonding domains. The less electronegative the central atom, the greater the deviation from ideal tetrahedral angles. The angles will vary as H2O > H2S > H2Se.
9.37 A bond dipole is the asymmetric charge distribution between two bonded atoms with unequal electronegativities. A molecular dipole moment is the three-dimensional sum of all the bond dipoles in a molecule.
9.39 (a) Yes. The net dipole moment vector points along the Cl — S — Cl angle bisector. (b) No, BeCl2 does not have a dipole moment.
9.41 (a) In Exercise 9.29, molecules (ii) and (iii) will have nonzero dipole moments. Molecule (i) has no nonbonding electron pairs on A, and the 3 A — F bond dipoles are oriented so that they cancel. Molecules (ii) and (iii) have nonbonding electron pairs on A and their bond dipoles do not cancel. (b) In Exercise 9.30, molecules (i) and (ii) have a zero dipole moment.
9.43 (a) IF (d) PCl3 and (f) IF5 are polar.
9.45
(b) The middle isomer has a zero net dipole moment. (c) C2H3Cl has only one isomer, and it has a dipole moment.
9.47 (a) Orbital overlap occurs when valence atomic orbitals on two adjacent atoms share the same region of space. (b) A chemical bond is a concentration of electron density between the nuclei of two atoms. This concentration can take place because orbitals on the two atoms overlap.
9.49 (a) H — Mg — H, linear electron domain and molecular geometry (b) The linear electron-domain geometry in MgH2 requires sp hybridization.
![]()
9.51
9.53 (a) B, [He]2s22p1. One 2s electron is “promoted” to an empty 2p orbital. The 2s and two 2p orbitals that each contain one electron are hybridized to form three equivalent hybrid orbitals in a trigonal-planar arrangement. (b) sp2 (d) A single 2p orbital is unhybridized. It lies perpendicular to the trigonal plane of the sp2 hybrid orbitals.
9.55 (a) sp2 (b) sp3 (c) sp (d) sp3
9.57 No hybrid orbitals discussed in this chapter form angles of 90° with each other; p atomic orbitals are perpendicular to each other. 109.5°, sp3; 120°, sp2
9.58
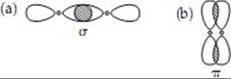
(c) A σ bond is generally stronger than a π bond because there is more extensive orbital overlap. (d) No. Overlap of two s orbitals results in electron density along the internuclear axis, while a π bond has none.

(b) sp3, sp2, sp (c) nonplanar, planar, planar (d) 7 σ, 0 π; 5 σ, 1 π; 3 σ, 2 π (e) The Si analogs would have the same hybridization as the C compounds given in part (b). That Si is in the row below C means it has a larger bonding atomic radius and atomic orbitals than C. The close approach of Si atoms required to form strong, stable π bonds in Si2H4 and Si2H2 is not possible and these Si analogs do not readily form.
9.63 (a) 18 valence electrons (b) 16 valence electrons form σ bonds. (c) 2 valence electrons form π bonds. (d) No valence electrons are nonbonding. (e) The left and central C atoms are sp2 hybridized; the right C atom is sp3 hybridized.
9.65 (a) ~ 109° about the leftmost C, sp3;~ 120° about the right-hand C, sp2 (b) The doubly bonded O can be viewed as sp2, and the other as sp3; the nitrogen is sp3 with approximately 109° bond angles. (c) nine σ bonds, one π bond
9.67 (a) In a localized π bond, the electron density is concentrated between the two atoms forming the bond. In a delocalized π bond, the electron density is spread over all the atoms that contribute p orbitals to the network. (b) The existence of more than one resonance form is a good indication that a molecule will have delocalized π bonding. (c) delocalized
9.69 (a) Linear (b) The two central C atoms each have trigonal planar geometry with ~120° bond angles about them. The C and O atoms lie in a plane with the H atoms free to rotate in and out of this plane. (c) The molecule is planar with ~120° bond angles about the two N atoms.
9.71 (a) Hybrid orbitals are mixtures of atomic orbitals from a single atom and remain localized on that atom. Molecular orbitals are combinations of atomic orbitals from two or more atoms and are delocalized over at least two atoms. (b) Each MO can hold a maximum of two electrons. (c) Antibonding molecular orbitals can have electrons in them.
9.73
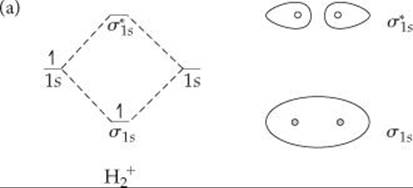
(b) There is one electron in H2+. (c) σ11s (d) BO = ![]() (e) Fall apart. If the single electron in H2+ is excited to the σs*1sorbital, its energy is higher than the energy of an H 1s atomic orbital and H2+ will decompose into a hydrogen atom and a hydrogen ion.
(e) Fall apart. If the single electron in H2+ is excited to the σs*1sorbital, its energy is higher than the energy of an H 1s atomic orbital and H2+ will decompose into a hydrogen atom and a hydrogen ion.
9.75
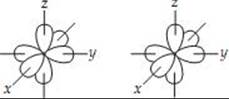
(a) 1 σ bond (b) 2 π bonds (c) 1 σ* and 2 π*
9.77 (a) When comparing the same two bonded atoms, bond order and bond energy are directly related, while bond order and bond length are inversely related. When comparing different bonded nuclei, there are no simple relationships. (b) Be2 is not expected to exist; it has a bond order of zero and is not energetically favored over isolated Be atoms. Be2+ has a bond order of 0.5 and is slightly lower in energy than isolated Be atoms. It will probably exist under special experimental conditions.
9.79 (a, b) Substances with no unpaired electrons are weakly repelled by a magnetic field. This property is called diamagnetism. (c) O22–, Be22+
9.81 (a) B2+, σ2s2σ*2s*2π2p1, increase (b) Li2+, σ1s2σ*1s2σ2s1, increase (c) N2+, σ2s2σ*2s2π2p4σ2p1, increase (d) Ne22+, σ2s2σ*2s2σ2p2π2p4π*2p4, decrease
9.83 CN, σ2s2σ*2s2σ2p2π2p3, bond order = 2.5; CN+, σ2s2σ*2s2σ2p2π2p2, bond order = 2.0; CN–, σ2s2σ*2s2σ2p2π2p4, bond order = 3.0. (a) CN– (b) CN, CN+
9.85 (a) 3s, 3px, 3py, 3pz (b) p3p (c) 2 (d) If the MO diagram for P2 is similar to that of N2, P2 will have no unpaired electrons and be diamagnetic.
9.89 SiF4 is tetrahedral, SF4 is seesaw, XeF4 is square planar. The shapes are different because the number of nonbonding electron domains is different in each molecule, even though all have four bonding electron domains. Bond angles and thus molecular shape are determined by the total number of electron domains.
9.92 (a) 2 σ bonds, 2 π bonds (b) 3 σ bonds, 4 π bonds (c) 3 σ bonds, 1 π bond (d) 4 σ bonds, 1 π bond
9.94 BF3 is trigonal planar, the B — F bond dipoles cancel and the molecule is nonpolar. PF3 has a tetrahedral electron-domain geometry with one position occupied by a nonbonding electron pair. The nonbonding electron pair ensures an asymmetrical electron distribution and the molecule is polar.
9.99

(a) The molecule is nonplanar. (b) Allene has no dipole moment. (c) The bonding in allene would not be described as delocalized. The π electron clouds of the two adjacent C ═ C are mutually perpendicular, so there is no overlap and no delocalization of π electrons.
9.101 (a) All O atoms have sp2 hybridization. (b) The two σ bonds are formed by overlap of sp2 hybrid orbitals, the π bond is formed by overlap of atomic p orbitals, one nonbonded pair is in a p atomic orbital and the other five nonbonded pairs are in sp2 hybrid orbitals. (c) unhybridized patomic orbitals (d) four, two from the π bond and two from the nonbonded pair in the p atomic orbital
9.104 σ2s2σ*2s2π2p4σ2p1π*2p1 (a) Paramagnetic (b) The bond order of N2 in the ground state is 3; in the first excited state it has a bond order of 2. Owing to the reduction in bond order, N2 in the first excited state has a weaker N — N bond.
9.110 (a) 2 SF4(g) + O2(g) ![]() 2 OSF4(g)
2 OSF4(g)
(c) ΔH = –551 kJ, exothermic (d) The electron-domain geometry is trigonal bipyramidal. The O atom can be either equatorial or axial. (e) Since F is more electronegative than O, the structure that minimizes 90° F — S — F angles, the one with O axial, is preferred.
CHAPTER 10
10.1 It would be much easier to drink from a straw on Mars. When a straw is placed in a glass of liquid, the atmosphere exerts equal pressure inside and outside the straw. When we drink through a straw, we withdraw air, thereby reducing the pressure on the liquid inside. If only 0.007 atm is exerted on the liquid in the glass, a very small reduction in pressure inside the straw will cause the liquid to rise.
10.4 (a) As the reaction proceeds at constant temperature and pressure, the number of particles decreases and the container volume decreases. (b) As the reaction proceeds at constant volume and temperature, the number of particles decreases and pressure decreases.
10.7 (a) Pred < Pyellow < Pblue (b) Pred = 0.28atm; Pyellow = 0.42atm; Pblue = 0.70atm
10.10 (a) P(ii) < P(i) = P(iii) (b) PHe(iii) < PHe(ii) < PHe(i) (c) d(ii) < d(i) < d(iii) (d) The average kinetic energies of the particles in the three containers are equal.
10.13 (a) A gas is much less dense than a liquid. (b) A gas is much more compressible than a liquid. (c) All mixtures of gases are homogenous. Similar liquid molecules form homogeneous mixtures, while very dissimilar molecules form heterogeneous mixtures. (d) Both gases and liquids conform to the shape of their container. A gas also adopts the volume of its container, while a liquid maintains its own volume.
10.15 (a) 1.8 × 103 kPa (b) 18 atm (c) 2.6 × 102 lb/in.2
10.17 (a) 10.3 m (b) 2.1 atm
10.19 (a) The tube can have any cross-sectional area. (b) At equilibrium the force of gravity per unit area acting on the mercury column is not equal to the force of gravity per unit area acting on the atmosphere. (c) The column of mercury is held up by the pressure of the atmosphere applied to the exterior pool of mercury. (d) If you took the mercury barometer with you on a trip from the beach to high mountains, the height of the mercury column would decrease with elevation.
10.21 (a) 0.349 atm (b) 265 mm Hg (c) 3.53 × 104 Pa (d) 0.353 bar (e) 5.13 psi
10.23 (a) P = 773.4 torr (b) P = 1.018atm (c) The pressure in Chicago is greater than standard atmospheric pressure, and so it makes sense to classify this weather system as a “high-pressure system.”
10.25 (i) 0.31 atm (ii) 1.88 atm (iii) 0.136 atm
10.27 (a) If V decreases by a factor of 4, P increases by a factor of 4. (b) If T decreases by a factor of 2, P decreases by a factor of 2. (c) If n decreases by a factor of 4, P decreases by a factor of 4.
10.29 (a) If equal volumes of gases at the same temperature and pressure contain equal numbers of molecules and molecules react in the ratios of small whole numbers, it follows that the volumes of reacting gases are in the ratios of small whole numbers. (b) Since the two gases are at the same temperature and pressure, the ratio of the numbers of atoms is the same as the ratio of volumes. There are 1.5 times as many Xe atoms as Ne atoms. (c) Yes. By definition, one mole of an ideal gas contains Avogadro's number of particles. At a given temperature and pressure, equal numbers of particles occupy the same volume, so one mole of an ideal gas will always occupy the same volume at the given temperature and pressure.
10.31 (a) An ideal gas exhibits pressure, volume, and temperature relationships described by the equation PV = nRT. (b) Boyle's law, V = constant/P; Charles's law, V = constant × T; Avogadro's law, V = constant × n. Collect all the equalities: V = (constant × T × n)/P. Call the constant Rand multiply both sides of the equation by P, PV = nRT. (c) PV = nRT; P in at mospheres, V in liters, n in moles, T in kelvins. (d) R = 0.08315 L-bar/mol-K.
10.33 Flask A contains the gas with M = 30 g/mol, and flask B contains the gas with M = 60 g/mol.
10.35
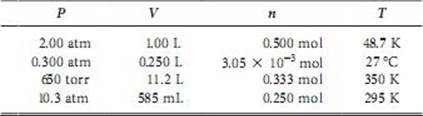
10.37 8.2 × 102 kg He
10.39 (a) 5.15 × 1022 molecules (b) 6.5 kg air
10.41 (a) 91 atm (b) 2.3 × 102 L
10.43 (a) 29.8 g Cl2 (b) 9.42 L (c) 501 K (d) 2.28 atm
10.45 (a) n = 2 × 10–4 mol O2 (b) The roach needs 8 × 10–3 mol O2 in 48 h, approximately 100% of the O2 in the jar.
10.47 (a) 1.32 × 107L (b) 5.1 × 108 mol Hg
10.49 For gas samples at the same conditions, molar mass determines density. Of the three gases listed, (c) Cl2 has the largest molar mass.
10.51 (c) Because the helium atoms are of lower mass than the average air molecule, the helium gas is less dense than air. The balloon thus weighs less than the air displaced by its volume.
10.53 (a) d = 1.77 g/L (b) M = 80.1 g/mol
10.55 M = 89.4 g/mol
10.57 4.1 × 10–9 g Mg
10.59 (a) 21.4 L CO2 (b) 40.7 L O2
10.61 0.402 g Zn
10.63 (a) When the stopcock is opened, the volume occupied by N2(g) increases from 2.0 L to 5.0 L. PN2 = 0.40 atm (b) When the gases mix, the volume of O2(g) increases from 3.0 L to 5.0 L. PO2 = 1.2 atm (c) Pt = 1.6 atm
10.65 (a) PHe = 1.87atm, PNe = 0.807atm, PAr = 0.269atm, (b) Pt = 2.95 atm
10.67 XcO2 = 0.00039
10.69 PCO2 = 0.305 atm, Pt = 1.232 atm
10.71 PN2 = 1.3 atm, PO2 = 0.54 atm, PCO2, = 0.27 atm
10.73 2.5 mole % O2
10.75 Pt = 2.47 atm
10.77 (a) Increase in temperature at constant volume or decrease in volume or increase in pressure (b) decrease in temperature (c) increase in volume, decrease in pressure (d) increase in temperature
10.79 The fact that gases are readily compressible supports the assumption that most of the volume of a gas sample is empty space.
10.81 Average speed is the sum of the speeds of all particles divided by the total number of particles. The root mean square speed is the speed of a molecule with the same kinetic energy as the average kinetic energy of the sample. The root mean square speed is larger for a given gas sample at a fixed temperature, but the difference between the two is small.
10.83 (a) Average kinetic energy of the molecules increases. (b) Root mean square speed of the molecules increases. (c) Strength of an average impact with the container walls increases. (d) Total collisions of molecules with walls per second increases.
10.85 (a) In order of increasing speed and decreasing molar mass: HBr < NF3 < S02 < CO < Ne (b) uNF3 = 324 m/s (c) The most probable speed of an ozone molecule in the stratosphere is 306 m/s.
10.87 Effusion is the escape of gas molecules through a tiny hole. Diffusion is the distribution of a gas throughout space or throughout another substance.
10.89 The order of increasing rate of effusion is 2H37C1 < 1H37C1 < 2H35C1 < 1H37C1
10.91 As4S6
10.93 (a) Non-ideal-gas behavior is observed at very high pressures and low temperatures. (b) The real volumes of gas molecules and attractive intermolecular forces between molecules cause gases to behave nonideally (c) According to the ideal-gas law, the ratio PV/RT should be constant for a given gas sample at all combinations of pressure, volume, and temperature. If this ratio changes with increasing pressure, the gas sample is not behaving ideally.
10.95 Ar (a = 1.34, b = 0.0322) will behave more like an ideal gas than CO2 (a = 3.59, b = 0.427) at high pressures.
10.97 (a) P = 4.89 atm (b) P = 4.69 atm (c) Qualitatively, molecular attractions are more important as the amount of free space decreases and the number of molecular collisions increases. Molecular volume is a larger part of the total volume as the container volume decreases.
10.99 From the value of b for Xe, the nonbonding radius is 2.72 Å. From Figure 7.6, the bonding atomic radius of Xe is 1.30 Å. We expect the bonding radius of an atom to be smaller than its nonbonding radius, but this difference is quite large.
10.101 V = 3.1mm3
10.105 (a) 13.4 mol C3H8(g) (b) 1.47 × 103 molC3H8(l) (c) The ratio of moles liquid to moles gas is 110. Many more molecules and moles of liquid fit in a container of fixed volume because there is much less space between molecules in the liquid phase.
10.108 Pt = 5.3 X 102torr
10.11142.2 g O2
10.115 T2 = 687 °C
10.120 (a) P(ideal) = 177 atm (b) P(van der Waals) = 187.4 atm (c) Under the conditions of this problem (large number of moles of gas), the correction for the real volume of molecules dominates.
10.123 (a) 44.58% C, 6.596% H, 16.44% Cl, 32.38% N (b) C8H14N5C1 (c) Molar mass of the compound is required in order to determine molecular formula when the empirical formula is known.
10.128 (a) 5.02 X 108 L CH3OH(l) (b) CH4(g) + 2 O2(g) ![]() CO2(g) + 2 H2O(l), ΔH° = –890.4 kj; ΔH for combustion of the methane is –1.10 X 1013kJ. CH3OH(/) + 3/2 02(g)
CO2(g) + 2 H2O(l), ΔH° = –890.4 kj; ΔH for combustion of the methane is –1.10 X 1013kJ. CH3OH(/) + 3/2 02(g) ![]() CO2(g) + 2 H2O(Z), ΔH° = —726.6 kj; ΔH for combustion of the methanol is –9.00 X 1012 kj. (c) The enthalpy change upon combustion of 1.00 L of CH4(l) is –2.59 × 104 kJ and for 1.00 L of CH3OH,(l), –1.79 × 104kJ. Clearly CH4(l) has the higher enthalpy of combustion per unit volume.
CO2(g) + 2 H2O(Z), ΔH° = —726.6 kj; ΔH for combustion of the methanol is –9.00 X 1012 kj. (c) The enthalpy change upon combustion of 1.00 L of CH4(l) is –2.59 × 104 kJ and for 1.00 L of CH3OH,(l), –1.79 × 104kJ. Clearly CH4(l) has the higher enthalpy of combustion per unit volume.
CHAPTER 11
11.1 The diagram best describes a liquid. The particles are close together, mostly touching, but there is no regular arrangement or order. This rules out a gaseous sample, where the particles are far apart, and a crystalline solid, which has a regular repeating structure in all three directions.
11.4 (a) In its final state, methane is a gas at 185 °C
11.5 (a) 385 mm Hg (b) 22 °C (c) 47 °C
11.6 The stronger the intermolecular forces, the higher the boiling point of a liquid. Propanol, CH3CH2CH2OH, has hydrogen bonding and the higher boiling point.
11.7 (a) Normal boiling point, 360 K; normal freezing point, 260 K(b)(i) gas (ii) solid (iii) liquid (c) The triple point is approximately 185 K at 0.45 atm.
11.9 (a) Solid < liquid < gas (b) gas < liquid < solid (c) Matter in the gaseous state is most easily compressed because particles are far apart and there is much empty space.
11.11 Ar < CCl4 < Si
11.13 (a) The molar volumes of Cl2 and NH3 are nearly the same because they are both gases. (b) On cooling to 160 K, both compounds condense from the gas phase to the solid-state, so we expect a significant decrease in the molar volume. (c) The molar volumes are 0.0351 L/mol Cl2 and 0.0203 L/mol NH3 (d) Solid-state molar volumes are not as similar as those in the gaseous state, because most of the empty space is gone and molecular characteristics determine properties. Cl2(s) is heavier, has a longer bond distance and weaker inter-molecular forces, so it has a significantly larger molar volume than NH3(s). (e) There is little empty space between molecules in the liquid state, so we expect their molar volumes to be closer to those in the solid state than those in the gaseous state.
11.15 (a) London dispersion forces (b) dipole–dipole and London dispersion forces dipole–dipole forces and in certain cases hydrogen bonding
11.17 (a) SO2, dipole–dipole and London dispersion forces (b) CH3COOH, London dispersion, dipole–dipole, and hydrogen bonding (c) H2Se, dipole–dipole and London dispersion forces (but not hydrogen bonding)
11.19 (a) Polarizability is the ease with which the charge distribution in a molecule can be distorted to produce a transient dipole. (b) Sb is most polarizable because its valence electrons are farthest from the nucleus and least tightly held. (c) in order of increasing polarizability: CH4 < SiH4 < SiCl4 < GeCl4 < GeBr4 (d) The magnitudes of London dispersion forces and thus the boiling points of molecules increase as polarizability increases. The order of increasing boiling points is the order of increasing polarizability given in (c).
11.21 (a) H2S (b) CO2 (c) GeH4
11.23 Both rodlike butane molecules and spherical 2-methylpropane molecules experience dispersion forces. The larger contact surface between butane molecules facilitates stronger forces and produces a higher boiling point.
11.25 (a) A molecule must contain H atoms, bound to either N, O, or F atoms, in order to participate in hydrogen bonding with like molecules. (b) CH3NH2 and CH3OH
11.27 (a) Replacing a hydroxyl hydrogen with a CH3 group eliminates hydrogen bonding in that part of the molecule. This reduces the strength of intermolecular forces and leads to a lower boiling point. (b) CH3OCH2CH2OCH3 is a larger, more polarizable molecule with stronger London dispersion forces and thus a higher boiling point.
11.29

(a) Based on its much higher normal melting point and boiling point, H2O has much stronger intermolecular forces. H2O has hydrogen bonding, while H2S has dipole–dipole forces. (b) H2S is probably a typical compound with less empty space in the ordered solid than the liquid, so that the solid is denser than the liquid. For H2O, maximizing the number of hydrogen bonds to each molecule in the solid requires more empty space than in the liquid, and the solid is less dense. (c) Specific heat is the energy required to raise the temperature of one gram of the substance one degree Celsius. Hydrogen bonding in water is such a strong attractive interaction that the energy required to disrupt it and increase molecular motion is large.
11.31 SO42– has a greater negative charge than BF4–, so ion–ion electrostatic attractions are greater in sulfate salts and they are less likely to form liquids.
11.33 (a) As temperature increases, the number of molecules with sufficient kinetic energy to overcome intermolecular attractive forces increases, and viscosity and surface tension decrease. (b) The same attractive forces that cause surface molecules to be difficult to separate (high surface tension) cause molecules elsewhere in the sample to resist movement relative to each other (high viscosity).
11.35 (a) CHBr3 has a higher molar mass, is more polarizable, and has stronger dispersion forces, so the surface tension is greater. (b) As temperature increases, the viscosity of the oil decreases because the average kinetic energy of the molecules increases. (c) Adhesive forces between polar water and nonpolar car wax are weak, so the large surface tension of water draws the liquid into the shape with the smallest surface area, a sphere. (d) Adhesive forces between nonpolar oil and nonpolar car wax are similar to cohesive forces in oil, so the oil drops spread out on the waxed car hood.
11.37 (a) The three molecules have similar structures and experience the same types of intermolecular forces. As molar mass increases, the strength of dispersion forces increases and the boiling points, surface tension, and viscosities all increase. (b) Ethylene glycol has an —OH group at both ends of the molecule. This greatly increases the possibilities for hydrogen bonding; the overall intermole-cular attractive forces are greater and the viscosity of ethylene glycol is much greater. (c) Water has the highest surface tension but lowest viscosity because it is the smallest molecule in the series. There is no hydrocarbon chain to inhibit their strong attraction to molecules in the interior of the drop, resulting in high surface tension. The absence of an alkyl chain also means the molecules can move around each other easily, resulting in the low viscosity.
11.39 (a) Melting, endothermic (b) evaporation, endothermic (c) deposition, exothermic (d) condensation, exothermic
11.41 Melting does not require separation of molecules, so the energy requirement is smaller than for vaporization, where molecules must be separated.
11.43 2.3 × 103 g H2O
11.45 (a) 39.3 kJ (b) 60 kJ
11.47 (a) The critical pressure is the pressure required to cause liquefaction at the critical temperature. (b) As the force of attraction between molecules increases, the critical temperature of the compound increases. (c) All the gases in Table 11.5 can be liquefied at the temperature of liquid nitrogen, given sufficient pressure.
11.49 (a) No effect (b) no effect (c) Vapor pressure decreases with increasing intermolecular attractive forces because fewer molecules have sufficient kinetic energy to overcome attractive forces and escape to the vapor phase. (d) Vapor pressure increases with increasing temperature because average kinetic energies of molecules increase. (e) Vapor pressure decreases with increasing density because attractive in-termolecular forces increase.
11.51 (a) CBr4 < CHBr3 < CH2Br2 < CH2Cl2 < CH3Cl < CH4. The trend is dominated by dispersion forces even though four of the molecules are polar. The order of increasing volatility is the order of increasing vapor pressure, decreasing molar mass, and decreasing strength of dispersion forces. (b) Boiling point increases as the strength of intermolecular forces increases; this is the order of decreasing volatility and the reverse of the order in part (a). CH4 < CH3Cl < CH2Cl2 < CH2Br2 < CHBr3 < CBr4
11.53 (a) The temperature of the water in the two pans is the same. (b) Vapor pressure does not depend on either volume or surface area of the liquid. At the same temperature, the vapor pressures of water in the two containers are the same.
11.55 (a) Approximately 48 °C (b) approximately 340 torr (c) approximately 17 °C (d) approximately 1000 torr
11.57 (a) The critical point is the temperature and pressure beyond which the gas and liquid phases are indistinguishable. (b) The line that separates the gas and liquid phases ends at the critical point because at conditions beyond the critical temperature and pressure, there is no distinction between gas and liquid. In experimental terms a gas cannot be liquefied at temperatures higher than the critical temperature, regardless of pressure.
11.59 (a) H2O(g) will condense to H2O(s) at approximately 4 torr; at a higher pressure, perhaps 5 atm or so, H2O(s) will melt to form H2O(l). (b) At 100 °C and 0.50 atm, water is in the vapor phase. As it cools, water vapor condenses to the liquid at approximately 82 °C, the temperature where the vapor pressure of liquid water is 0.50 atm. Further cooling results in freezing at approximately 0 °C. The freezing point of water increases with decreasing pressure, so at 0.50 atm the freezing temperature is very slightly above 0 °C.
11.61 (a) 24 K (b) Neon sublimes at pressures less than the triple point pressure, 0.43 atm. (c) No
11.63 (a) Methane on the surface of Titan is likely to exist in both solid and liquid forms. (b) As pressure decreases upon moving away from the surface of Titan, CH4(l) (at –178 °C) will vaporize to CH4(g), and CH4(s) (at temperatures below –180 °C) will sublime to CH4(g).
11.65 In a nematic liquid crystalline phase, molecules are aligned along their long axes, but the molecular ends are not aligned. Molecules are free to translate in all dimensions, but they cannot tumble or rotate out of the molecular plane, or the order of the nematic phase is lost and the sample becomes an ordinary liquid. In an ordinary liquid, molecules are randomly oriented and free to move in any direction.
11.67 The presence of polar groups or nonbonded electron pairs leads to relatively strong dipole–dipole interactions between molecules. These are a significant part of the orienting forces necessary for liquid crystal formation.
11.69 Because order is maintained in at least one dimension, the molecules in a liquid-crystalline phase are not totally free to change orientation. This makes the liquid-crystalline phase more resistant to flow, more viscous, than the isotropic liquid.
11.71 Melting provides kinetic energy sufficient to disrupt molecular alignment in one dimension in the solid, producing a smectic phase with ordering in two dimensions. Additional heating of the smectic phase provides kinetic energy sufficient to disrupt alignment in another dimension, producing a nematic phase with one-dimensional order.
11.73 (a) Decrease (b) increase (c) increase (d) increase (e) increase (f) increase (g) increase
11.77 When a halogen is substituted for H in benzene, molar mass, polarizability and strength of dispersion forces increase; the order of increasing molar mass is the order of increasing boiling points for the first three compounds. C6H5OH experiences hydrogen bonding, the strongest force between neutral molecules, so it has the highest boiling point.
11.82 (a) Evaporation is an endothermic process. The heat required to vaporize sweat is absorbed from your body, helping to keep it cool. (b) The vacuum pump reduces the pressure of the atmosphere above the water until atmospheric pressure equals the vapor pressure of water and the water boils. Boiling is an endothermic process, and the temperature drops if the system is not able to absorb heat from the surroundings fast enough. As the temperature of the water decreases, the water freezes.
11.86 At low Antarctic temperatures, molecules in the liquid crystalline phase have less kinetic energy due to temperature, and the applied voltage may not be sufficient to overcome orienting forces among the ends of molecules. If some or all of the molecules do not rotate when the voltage is applied, the display will not function properly.
11.90
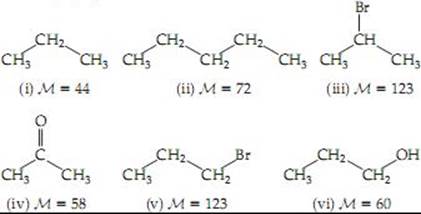
(a) Molar mass: Compounds (i) and (ii) have similar rodlike structures. The longer chain in (ii) leads to greater molar mass, stronger London dispersion forces, and higher heat of vaporization. (b) Molecular shape: Compounds (iii) and (v) have the same chemical formula and molar mass but different molecular shapes. The more rodlike shape of (v) leads to more contact between molecules, stronger dispersion forces, and higher heat of vaporization. (c) Molecular polarity: Compound (iv) has a smaller molar mass than (ii) but a larger heat of vaporization, which must be due to the presence of dipole–dipole forces. (d) Hydrogen bonding interactions: Molecules (v) and (vi) have similar structures. Even though (v) has larger molar mass and dispersion forces, hydrogen bonding causes (vi) to have the higher heat of vaporization.
11.93 P(benzene vapor) = 98.7 torr
CHAPTER 12
12.1
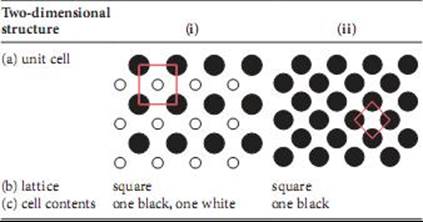
12.3 (a) 1 Re and 3 O atoms per unit cell (b) 3.92 Å (c) 6.46 g/cm3
12.5 We expect linear polymer (a), with ordered regions, to be denser and have a higher melting point than branched polymer (b).
12.7 In molecular solids, relatively weak intermolecular forces bind the molecules in the lattice, so relatively little energy is required to disrupt these forces. In covalent-network solids, covalent bonds join atoms into an extended network. Melting or deforming a covalent-network solid means breaking covalent bonds, which requires a large amount of energy.
12.9 (a) Hydrogen bonding, dipole-dipole forces, London dispersion forces (b) covalent chemical bonds (c) ionic bonds (d) metallic bonds
12.11 (a) Ionic (b) metallic (c) covalent-network (It could also be characterized as ionic with some covalent character to the bonds.) (d) molecular (e) molecular (f) molecular
12.13 Because of its relatively high melting point and properties as a conducting solution, the solid must be ionic.
12.15
12.17
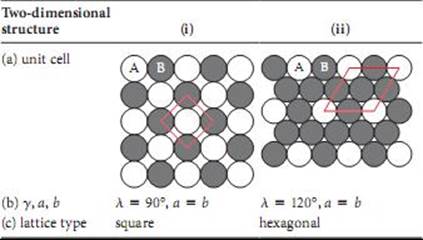
12.19 (a) Orthorhombic (d) tetragonal
12.21 Triclinic, rhombohedral
12.23 There is a minimum of two (metal) atoms in a bodycentered cubic unit cell.
12.25 (a) Primitive hexagonal unit cell (b) NiAs
12.27 Moving left to right in the period, atomic mass and Zeff increase. The increase in Zeff leads to smaller bonding atomic radii and atomic volume. Mass increases, volume decreases, and density increases in the series. The variation in densities reflects shorter metal–metal bond distances and an increase in the extent of metal–metal bonding. The strength of metal–metal bonds in the series is probably the most important factor influencing the increase in density.
12.29 (a) Structure types A and C have equally dense packing and are more densely packed than structure type B. (b) Structure type B is least densely packed.
12.31 (a) The radius of an Ir atom is 1.355 Å. (b) The density of Ir is 22.67 g/cm3
12.33 (a) 4 Al atoms per unit cell (b) coordination number = 12 (c) a = 4.04 Å or 4.04 × 10–8 cm (d) density = 2.71 g/cm3
12.35 An alloy contains atoms of more than one element and has the properties of a metal. In a solution alloy the components are randomly dispersed. In a heterogeneous alloy the components are not evenly dispersed and can be distinguished at a macroscopic level. In an intermetallic compound the components have interacted to form a compound substance, as in Cu3As.
12.37 (a) Interstitial alloy (b) substitutional alloy (c) intermetallic compound
12.39 (a) True (b) false (c) false
12.41 (a) Nickel or palladium, substitutional alloy (b) copper, substitutional alloy (c) indium, intermetallic compound (d) silver, substitutional alloy
12.43 In the electron-sea model, valence electrons move about the metallic lattice, while metal atoms remain more or less fixed in position. Under the influence of an applied potential, the electrons are free to move throughout the structure, giving rise to thermal and electrical conductivity.
12.45
(a) Six AOs require six MOs (b) zero nodes in the lowest energy orbital (c) five nodes in highest energy orbital (d) two nodes in the HOMO (e) three nodes in the LUMO.
12.47 (a) Ag (b) Zn. Ductility decreases as the strength of metal–metal bonding increases, producing a stiffer lattice, less susceptible to distortion.
12.49 Moving from Y to Mo, the number of valence electrons, occupancy of the bonding band, and strength of metallic bonding increase. Stronger metallic bonding requires more energy to break bonds and mobilize atoms, resulting in higher melting points.
12.51 (a) SrTiO3 (b) Each Sr atom is coordinated to twelve O atoms in eight unit cells that contain the Sr atom.
12.53 (a) a = 4.70 Å (b) 2.69 g/cm3
12.55 (a) 7.711 g/cm3 (b) We expect Se2– to have a larger ionic radius than S2–, so HgSe will occupy a larger volume and the unit cell edge will be longer. (c) The density of HgSe is 8.241 g/cm3. The greater mass of Se accounts for the greater density of HgSe.
12.57 (a) Cs+ and I– have the most similar radii and will adopt the CsCl-type structure. The radii of Na+ and I– are somewhat different; NaI will adopt the NaCl-type structure. The radii of Cu+ and I– are very different; CuI has the ZnS-type structure. CsI, 8; NaI, 6; CuI, 4
12.59 (a) 6 (b) 3 (c) 6
12.61 (a) False (b) true
12.63 (a) Ionic solids are much more likely to dissolve in water. (b) Covalent-network solids can become electrical conductors via chemical substitution.
12.65 (a) CdS (b) GaN (c) GaAs
12.67 Ge or Si (Ge is closer to Ga in bonding atomic radius.)
12.69 (a) A 1.1 eV photon corresponds to a wavelength of 1.1 × 10–6 m. (b) According to the figure, Si can absorb a portion of the visible light that comes from the sun.
12.71 λ = 560 nm
12.73 The band gap is approximately 1.85 e V, which corresponds to a wavelength of 672 nm.
12.75 Monomers are small molecules with low molecular mass that are joined together to form polymers. Three monomers mentioned in this chapter are
12.77
If a dicarboxylic acid and a dialcohol are combined, there is the potential for propagation of the polymer chain at both ends of both monomers.
12.79
12.81

12.83 Flexibility of molecular chains causes flexibility of the bulk polymer. Flexibility is enhanced by molecular features that inhibit order, such as branching, and diminished by features that encourage order, such as cross-linking or delocalized π electron density. Cross-linking, the formation of chemical bonds between polymer chains, reduces flexibility of the molecular chains, increases the hardness of the material, and decreases the chemical reactivity of the polymer.
12.85 No. The function of the polymer determines whether high molecular mass and high degree of crystallinity are desirable properties. If the polymer will be used as a flexible wrapping or fiber, rigidity that is due to high molecular mass is an undesirable property.
12.87 If a solid has nanoscale dimensions of 1–10 nm, there may not be enough atoms contributing atomic orbitals to produce continuous energy bands of molecular orbitals.
12.89 (a) False. As particle size decreases, the band gap increases. (b) False. As particle size decreases, wavelength decreases.
12.91 2.47 × 105 Au atoms
12.94 The face-centered structure will have the greater density.
12.98 (a) CsCl, primitive cubic lattice (b) Au, face-centered cubic lattice (c) NaCl, face-centered cubic lattice (d) Po, primitive cubic lattice, rare for metals (e) ZnS, face-centered cubic lattice
12.99 White tin has a structure characteristic of a metal, while gray tin has the diamond structure characteristic of group 4A semiconductors. Metallic white tin has the longer bond distance because the valence electrons are shared with twelve nearest neighbors rather than being localized in four bonds as in gray tin.
12.103
TeflonTM is formed by addition polymerization.
12.105 Diffraction, the phenomenon that enables us to measure interatomic distances in crystals, is most efficient when the wavelength of light is similar to or smaller than the size of the object doing the diffracting. Atom sizes are on the order of 1–10 Å, and the wavelengths of X-rays are also in this range. Visible light, 400–700 nm or 4000–7000 Å, is too long to be diffracted effectively by atoms (electrons) in crystals.
12.107 In a diffraction experiment, we expect a Ge crystal to diffract X-rays at a smaller θ angle than a Si crystal, assuming the X-rays have the same wavelength.
12.109 (a) The bonds in a semiconductor will be weakened by n-type doping. (b) The bonds in a semiconductor will also be weakened by π-type doping.
12.112 (a) 109° (b) 120°
12.113 (a) ΔH = –82 kJ/mol (b) ΔH = –14 kJ/mol (of either reactant) (c) ΔH = 0 kJ
CHAPTER 13
13.1 (a) < (b) < (c)
13.3 The greater the lattice energy of an ionic solid, the more endothermic the dissolving process and the less soluble the salt in water.
13.7 Vitamin B6 is largely water soluble because of its small size and capacity for extensive hydrogen-bonding interactions. Vitamin E is largely fat soluble. The long, rodlike hydrocarbon chain will lead to strong dispersion forces among vitamin E and mostly nonpolar fats.
13.9 (a) Yes, the molarity changes with a change in temperature. Molarity is defined as moles solute per unit volume of solution. A change of temperature changes solution volume and molarity. (b) No, molality does not change with change in temperature. Molality is defined as moles solute per kilogram of solvent. Temperature affects neither mass nor moles.
13.13 If the magnitude of ΔHmix is small relative to the magnitude of ΔHsolute, ΔHsoln will be large and endothermic (energetically unfavorable) and not much solute will dissolve.
13.15 (a) Dispersion (b) hydrogen bonding (c) ion–dipole (d) dipole–dipole
13.17 Very soluble. In order for ΔHsoln to be negative, ΔHmix must have a greater magnitude than (ΔHsolute + ΔHsolvent). The entropy of mixing always encourages solubility. In this case, the enthalpy of the system decreases and the entropy increases, so the ionic compound dissolves.
13.19 (a) ΔHsolute (b) ΔHmix
13.21 (a) Since the solute and solvent experience very similar London dispersion forces, the energy required to separate them individually and the energy released when they are mixed are approximately equal. ΔHsolute + ΔHsolvent ≈ –ΔHmix. Thus, ΔHsoln is nearly zero. (b) Since no strong intermolecular forces prevent the molecules from mixing, they do so spontaneously because of the increase in randomness.
13.23 (a) Supersaturated (b) Add a seed crystal. A seed crystal provides a nucleus of prealigned molecules, so that ordering of the dissolved particles (crystallization) is more facile.
13.25 (a) Unsaturated (b) saturated (c) saturated (d) unsaturated
13.27 The liquids water and glycerol form homogenous mixtures (solutions) regardless of the relative amounts of the two components. The —OH groups of glycerol facilitate strong hydrogen bonding similar to that in water; like dissolves like.
13.29 Toluene, C6H5CH3, is the best solvent for nonpolar solutes. Without polar groups or nonbonding electron pairs, it forms only dispersion interactions with itself and other molecules.
13.31 (a) Dispersion interactions among nonpolar CH3(CH2)16 — chains dominate the properties of stearic acid, causing it to be more soluble in nonpolar CCl4. (b) Dioxane can act as a hydrogen bond acceptor, so it will be more soluble than cyclohexane in water.
13.33 (a) CCl4 is more soluble because dispersion forces among nonpolar CCl4 molecules are similar to dispersion forces in hexane. (b) C6H6 is a nonpolar hydrocarbon and will be more soluble in the similarly nonpolar hexane. (c) The long, rodlike hydrocarbon chain of octanoic acid forms strong dispersion interactions and causes it to be more soluble in hexane.
13.35 (a) A sealed container is required to maintain a partial pressure of CO2(g) greater than 1 atm above the beverage. (b) Since the solubility of gases increases with decreasing temperature, more CO2(g) will remain dissolved in the beverage if it is kept cool.
13.37 SHe = 5.6 × 10–4M, SN2 = 9.0 × 10–4M
13.39 (a) 2.15% Na2SO4 by mass (b) 3.15 ppm Ag
13.41 (a) XCH3OH = 0.0427 (b) 7.35% CH3OH by mass (c) 2.48 m CH3OH
13.43 (a) 1.46 × 10–2M Mg(NO3)2 (b) 1.12 M LiClO4 • 3 H2O (c) 0.350 MHNO3
13.45 (a) 4.70 mC6H6 (b) 0.235 mNaCl
13.47 (a) 43.01% H2SO4 by mass (b) XH2SO4 = 0.122 (c) 7.69 mH2SO4 (d) 5.827 MH2SO4
13.49 (a) XCH3OH = 0.227 (b) 7.16 m CH3OH (c) 4.58 MCH3OH
13.51 (a) 0.150 mol SrBr2 (b) 1.56 × 10–2 mol KCl (c) 4.44 × 10 –2 mol C6H12O6
13.53 (a) Weigh out 1.3 g KBr, dissolve in water, dilute with stirring to 0.75 L. (b) Weigh out 2.62 g KBr, dissolve it in 122.38 g H2O to make exactly 125 g of 0.180 m solution. (c) Dissolve 244 g KBr in water, dilute with stirring to 1.85 L. (d) Weigh 10.1 g KBr, dissolve it in a small amount of water, and dilute to 0.568 L.
13.55 71% HNO3 by mass
13.57 (a) 3.82 mZn (b) 26.8 M Zn
13.59 1.8 × 10–3MCO2
13.61 Freezing point depression, ΔTf = Kf(m); boiling-point elevation, ΔTb = Kb(m); osmotic pressure, π = MRT; vapor pressure lowering, PA = XAPA°
13.63 (a) Sucrose has a greater molar mass than glucose, so the sucrose solution will contain fewer particles and have a higher vapor pressure.
13.65 (a) PH2O = 186.4 torr (b) 78.9 g C3H8O2
13.67 (a) XEth = 0.2812 (b) Psoln = 238 torr (c) XEth in vapor = 0.472
13.69 (a) Because NaCl is a strong electrolyte, one mole of NaCl produces twice as many dissolved particles as one mole of the molecular solute C6H12O6. Boiling-point elevation is directly related to total moles of dissolved particles, so 0.10 mNaCl has the higher boiling point. (b) 0.10mNaCl: ΔTb = 0.101 °C, Tb = 100.1 °C; 0.10 mC6H12O6: ΔTb = 0.051 °C, Tb = 100.1 °C (c) Interactions between ions in solution result in nonideal behavior.
13.71 0.050 mLiBr < 0.120 mglucose < 0.050 m Zn(NO3)2
13.73 (a) Tf = –115.0 °C, Tb = 78.7 °C (b) Tf = –67.3 °C, Tb = 64.2 °C (c) Tf = –0.4°C, Tb = 100.1°C (c) Tf = –0.6°C, Tb = 100.2°C
13.75 167 g C2H6O2
13.77 P = 0.0168atm = 12.7torr
13.79 Experimental molar mass of adrenaline is 1.8 × 102 g. The structure shows a molecular formula of C9H13NO3, with a molar mass of 183 g. The two values agree to two significant figures, the precision of the experiment.
13.81 Molar mass of lysozyme = 1.39 × 104 g
13.83 (a) i = 2.8 (b) The more concentrated the solution, the greater the ion pairing and the smaller the measured value of i.
13.85 (a) In the gaseous state, particles are far apart and intermolecular attractive forces are small. When two gases combine, all terms in Equation 13.1 are essentially zero and the mixture is always homogeneous. (b) To determine whether Faraday's dispersion is a true solution or a colloid, shine a beam of light on it. If light is scattered, the dispersion is a colloid.
13.87 (a) Hydrophobic hydrophilic (c) hydrophobic (d) hydrophobic (but stabilized by adsorbed charges).
13.89 When electrolytes are added to a suspension of proteins, dissolved ions form ion pairs with the protein surface charges, effectively neutralizing them. The protein's capacity for ion–dipole interactions with water is diminished and the colloid separates into a protein layer and a water layer.
13.91 The periphery of the BHT molecule is mostly hydrocarbon-like groups, such as —CH3. The one —OH group is rather buried inside and probably does little to enhance solubility in water. Thus, BHT is more likely to be soluble in the nonpolar hydrocarbon hexane, C6H14, than in polar water.
13.94 (a) kRn = 7.27 × 10 –3 mol/L-atm (b) PRn = 1.1 × 10 –4 atm; SRn = 8.1 × 10 –7M
13.98 (a) 2.69 mLiBr (b) XLiBr = 0.0994 81.1% LiBr by mass
13.100 XH2O = 0.808; 0.0273 mol ions; 0.0136 mol NaCl
13.103 (a) –0.6 °C (b) –0.4°C
13.106 (a) CF4, 1.7 × 10–4m; CClF3, 9 × 10 –4m; CCl2F2, 2.3 × 10–2m; CHClF2, 3.5 × 10 –2m (b) Molality and molarity are numerically similar when kilograms solvent and liters solution are nearly equal. This is true when solutions are dilute and when the density of the solvent is nearly 1 g/mL, as in this exercise. (c) Water is a polar solvent; the solubility of solutes increases as their polarity increases. Nonpolar CF4 has the lowest solubility and the most polar fluorocarbon, CHClF2, has the greatest solubility in H2O. (d) The Henry's law constant for CHClF2 is 3.5 × 10 –2mol/L-atm. This value is greater than the Henry's law constant for N2(g) because N2(g) is nonpolar and of lower molecular mass than CHClF2.
13.109
(b) Lattice energy (U) is inversely related to the distance between ions, so salts with large cations like (CH3)4N+ have smaller lattice energies than salts with simple cations like Na+. Also the —CH3 groups in the large cation are capable of dispersion interactions with nonpolar groups of the solvent molecules, resulting in a more negative solvation energy of the gaseous ions. Overall, for salts with larger cations, lattice energy is smaller (less positive), the solvation energy of the gaseous ions is more negative, and ΔHsoln is less endothermic. These salts are more soluble in polar nonaqueous solvents.
13.112 The freezing point of the LiOH(aq) solution is essentially zero, Tf = –0.00058 °C.
CHAPTER 14
14.1 Vessel 2
14.3 Equation (d)
14.9 (1) Total potential energy of the reactants (2) Ea, activation energy of the reaction (3) ΔE, net energy change for the reaction (4) total potential energy of the products
14.12 (a) NO2 + F2![]() NO2F + F; NO2 + F
NO2F + F; NO2 + F ![]() NO2 + F
NO2 + F ![]() NO2F (b) 2NO2F(c) F (atomic fluorine) is the intermediate (d) rate = k[NO2][F2])
NO2F (b) 2NO2F(c) F (atomic fluorine) is the intermediate (d) rate = k[NO2][F2])
14.16
14.17 (a) Reaction rate is the change in the amount of products or reactants in a given amount of time. (b) Rates depend on concentration of reactants, surface area of reactants, temperature, and presence of catalyst. (c) The stoichiometry of the reaction (mole ratios of reactants and products) must be known to relate rate of disappearance of reactants to rate of appearance of products.
14.19
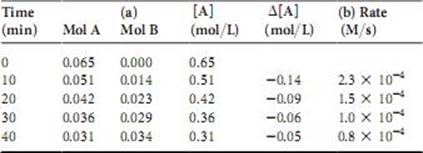
(c) Δ[B]avg/Δ t = 1.3 × 10–4M/s
14.21 (a)
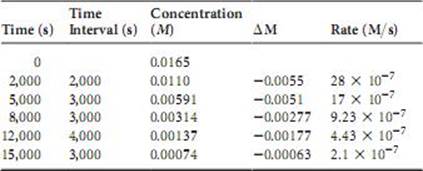
(b) The average rate of reaction is 1.05 × 10–6M/s. (c) From the slopes of the tangents to the graph, the rates are 12 × 10–7M/s at 5000 s, 5.8 × 10–7M/s at 8000 s.
14.23
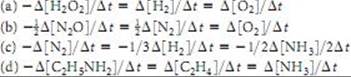
14.25 (a) – Δ[O2]/Δt = 0.24 mol/s; Δ[H2O]/Δt = 0.48 mol/s (b) Ptotal decreases by 28 torr/min.
14.27 (a) If [A] doubles, there is no change in the rate or the rate constant. The overall rate is unchanged because [A] does not appear in the rate law; the rate constant changes only with a change in temperature. (b) The reaction is zero order in A, second order in B, and second order overall. (c) units of k = M–1 s–1
14.29 (a) Rate = k[N2O5] (b) Rate = 1.16 × 10–4M/s (c) When the concentration of N2O5 doubles, the rate doubles. (d) When the concentration of N2O5 is halved, the rate doubles.
14.31 (a, b) k = 1.7 102M–1 s–1 (c) If [OH–] is tripled, the rate triples. (d) If [OH–] and [CH3Br] both triple, the rate increases by a factor of 9.
14.33 (a) Rate = k[OCI–][I–] (b) k = 60 M–1 s–1 (c) Rate = 6.0 × 10–5M/s
14.35 (a) Rate = k[BF3][NH3] (b) The reaction is second order overall. (c) kavg = 3.41 M–1 s–1 (d) 0.170 M/s
14.37 (a) Rate = k[NO]2[Br2] (b) kavg = 1.2 × 104M–2 s–1![]()
14.39 (a) [A]0 is the molar concentration of reactant A at time zero. [A]t is the molar concentration of reactant A at time t. t1/2 is the time required to reduce [A]0 by a factor of 2. k is the rate constant for a particular reaction. (b) A graph of ln[A] versus time yields a straight line for a first-order reaction. (c) On a graph of ln[A] versus time, the rate constant is the (–slope) of the straight line.
14.41 Plot [A] versus time.
14.43 (a) k = 3.0 × 10–6 s–1 (b) t1/2 = 3.2 × 104 s
14.45 (a) P = 30 torr (b) t = 51 s
14.47 Plot (ln PSO2Cl2) versus time, k = –slope = 2.19 × 10–5 s–1
14.49 (a) The plot of 1/[A] versus time is linear, so the reaction is second order in [A]. (b) k = 0.040 M–1 min–1 (c) t1/2 = 38 min
14.51 (a) The plot of I/[NO2] versus time is linear, so the reaction is second order in NO2. (b) k = slope = 10 M–1 s–1 (c) rate at 0.200 M = 0.400 M/s; rate at 0.100 M = 0.100 M/s; rate at 0.050 M = 0.025 M/s
14.53 (a) The energy of the collision and the orientation of the molecules when they collide determine whether a reaction will occur. (b) At a higher temperature, there are more total collisions and each collision is more energetic. (c) The rate constant usually increases with an increase in reaction temperature.
14.55 f = 4.94 × 10–2. At 400 K approximately 1 out of 20 molecules has this kinetic energy.
14.57 (a)
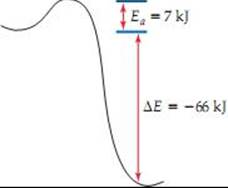
(b) Ea (reverse) = 73 kJ
14.59 (a) False. If you compare two reactions with similar collision factors, the one with the larger activation energy will be slower. (b) False. A reaction that has a small rate constant will have either a small frequency factor, a large activation energy, or both. (c) True.
14.61 Reaction (b) is fastest and reaction (c) is slowest.
14.63 (a) k = 1.1 s–1 (b) k = 13 s–1 (c) The method in parts (a) and (b) assumes that the collision model and thus the Arrhenious equation describe the kinetics of the reactions. That is, activation energy is constant over the temperature range under consideration.
14.65 A plot of ln k versus 1/T has a slope of –5.71 × 103; Ea = –R(slope) = 47.5 kJ/mol.
14.67 The reaction will occur 88 times faster at 50 °C, assuming equal initial concentrations.
14.69 (a) An elementary reaction is a process that occurs in a single event; the order is given by the coefficients in the balanced equation for the reaction. (b) A unimolecular elementary reaction involves only one reactant molecule; a bimolecular elementary reaction involves two reactant molecules. (c) A reaction mechanism is a series of elementary reactions that describes how an overall reaction occurs and explains the experimentally determined rate law.
14.71 A transition state is a high-energy complex formed when one or more reactants collide and distort in a way that can lead to formation of product(s). An intermediate is the product of an early elementary reaction in a multistep reaction mechanism.
14.73 (a) Unimolecular, rate = k[Cl2] (b) bimo- lecular, rate = k[OCI–][H2O] (c) bimolecular, rate = k[NO][Cl2]
14.75 (a) Two intermediates, B and C. (b) three transition states (c) C ![]() D is fastest. (d) endothermic
D is fastest. (d) endothermic
14.77 (a) H2(g) + 2 ICI(g) ![]() I2(g) + 2HCI(g) (b) HI is the intermediate. (c) If the first step is slow, the observed rate law is rate = k[H2][ICI].
I2(g) + 2HCI(g) (b) HI is the intermediate. (c) If the first step is slow, the observed rate law is rate = k[H2][ICI].
14.79 The graph of 1/[NO] versus time is linear with positive slope, indicating that the reaction is second order in [NO]. The rate law obtained by assuming the second step is rate determining is rate = [NO]2[Cl2]. The two-step mechanism is consistent with the data.
14.81 (a) A catalyst is a substance that changes (usually increases) the speed of a chemical reaction without undergoing a permanent chemical change itself. (b) A homogeneous catalyst is in the same phase as the reactants, while a hetereogeneous catalyst is in a different phase. (c) A catalyst has no effect on the overall enthalpy change for a reaction, but it does affect activation energy. It can also affect the frequency factor.
14.83 (a) 270 Pt atoms in a 2.0-nm sphere (b) 200 Pt atoms on the surface of a 2.0-nm sphere (c) 74% Pt atoms on the surface (d) 4300 Pt atoms in a 5.0-nm sphere; 1300 Pt atoms on the surface; 30% Pt atoms on the surface (e) The 2-nm sphere will definitely be more catalytically active because it has a much greater percentage of its atoms on the surface where they can participate in the chemical reaction.
14.85 (a) Multiply the coefficients in the first reaction by 2 and sum. (b) NO2(g) is a catalyst because it is consumed and then reproduced in the reaction sequence. (c) This is a homogeneous catalysis.
14.87 (a) Use of chemically stable supports makes it possible to obtain very large surface areas per unit mass of the precious metal catalyst because the metal can be deposited in a very thin, even monomolecular, layer on the surface of the support. (b) The greater the surface area of the catalyst, the more reaction sites, the greater the rate of the catalyzed reaction.
14.89 To put two D atoms on a single carbon, it is necessary that one of the already existing C — H bonds in ethylene be broken while the molecule is adsorbed, so that the H atom moves off as an adsorbed atom and is replaced by a D atom. This requires a larger activation energy than simply adsorbing C2H4 and adding one D atom to each carbon.
14.91 (a) Living organisms operate efficiently in a very narrow temperature range; the role of enzymes as homogeneous catalysts that speed up desirable reactions, without heating and undesirable side effects, is crucial for biological systems. (b) catalase: 2 H2O2![]() 2 H2O + O2; nitrogenase: N2
2 H2O + O2; nitrogenase: N2![]() 2 NH3 (nitrogen fixation) (c) This model assumes that the rate of the bound substrate being chemically transformed into bound product is slow and rate determining.
2 NH3 (nitrogen fixation) (c) This model assumes that the rate of the bound substrate being chemically transformed into bound product is slow and rate determining.
14.93 Carbonic anyhdrase lowers the activation energy of the reaction by 42 kJ.
14.95 (a) The catalyzed reaction is approximately 10,000,000 times faster at 25 °C. (b) The catalyzed reaction is 180,000 times faster at 125 °C.
14.99 (a) Rate = 4.7 × 10–5M/s (b, c) k = 0.84 M–2 s–1 (d) If the [NO] is increased by a factor of 1.8, the rate would increase by a factor of 3.2.
14.101 The reaction is second order in NO2. If and [NO2]0 = 0.100 M and [NO2]t = 0.025 M, use the integrated form of the second-order rate equation to solve for t = 48 s.
14.105 (a) The half-life of is 241 Am is 4.3 × 102 yr, that of 125I is 63 days (b) 125I decays at a much faster rate. (c) 0.13 mg of each isotope remains after 3 half-lives. (d) The amount of 241 Am remaining after 4 days is 1.00 mg. The amount of 125I remaining after 4 days is 0.957 grams.
14.109 The plot of 1/[C5H6] versus time is linear and the reaction is second order. k = 0.167 M–1 s–1
14.112 (a) When the two elementary reactions are added, N2O2(g) appears on both sides and cancels, resulting in the overall reaction. 2NO(g) + H2(g) ![]() N2O(g) + H2O(g) (b) First reaction, –[NO]/Δt = k[NO]2; second reaction, –[H2]/Δt = k[H2][N2O2] (c) N2O2 is the intermediate. (d) Since [H2] appears in the rate law, the second step must be slow relative to the first.
N2O(g) + H2O(g) (b) First reaction, –[NO]/Δt = k[NO]2; second reaction, –[H2]/Δt = k[H2][N2O2] (c) N2O2 is the intermediate. (d) Since [H2] appears in the rate law, the second step must be slow relative to the first.
14.115 (a) Cl2(g) + CHCl3(g) ![]() HCl(g) + CCl4(g) (b) Cl(g), CCl3(g) (c) reaction 1, unimolecular; reaction 2, bimolecular; reaction 3, bimolecular (d) Reaction 2 is rate determining. (e) Rate = k[CHCl3][Cl2]1/2.
HCl(g) + CCl4(g) (b) Cl(g), CCl3(g) (c) reaction 1, unimolecular; reaction 2, bimolecular; reaction 3, bimolecular (d) Reaction 2 is rate determining. (e) Rate = k[CHCl3][Cl2]1/2.
14.122 (a) k = 8 × 107M–1 s–1
(b) 
(c) NOF is bent with a bond angle of approximately 120°.
(d)![]()
(e) The electron-deficient NO molecule is attracted to electron-rich F2, so the driving force for formation of the transition state is greater than simple random collisions.
CHAPTER 15
15.1 kf > kr (b) The equilibrium constant is greater than 1.
15.7 From the smallest to the largest equilibrium constant, (c) < (b) < (a).
15.11Kc decreases as T increases, so the reaction is exothermic.
15.13 (a) Kp = Kc = 8.1 × 10–3. (b) Since kf < kr, in order for the two rates to be equal, [A] must be greater than [B], and the partial pressure of A is greater than the partial pressure of B.
15.15 (a) Kc = [N2O][NO2]/[NO]3; homogeneous (b) Kc = [CS2][H2]4/[CH4][H2S]2; homogeneous (c) Kc =[CO]4/[Ni(CO)4]; heterogeneous (d) Kc = [H+][OH–]; homogeneous (e) Kc = [Ag+]2/[Zn2+]; heterogeneous (f)Kc = [H+][OH–]; homogeneous (g) Kc = [H+][OH–]; homogeneous
15.17 (a) Mostly reactants (b) mostly products
15.19 No, the equilibrium constant can never be a negative number. The equilibrium constant is a ratio of rate constants (or a ratio of concentrations), which are never negative.
15.21 Kp = 1.0×10–3
15.23 (a) The equilibrium favors NO and Br2 at this temperature. (b) Kc = 77 (c) Kc = 8.8
15.25 (a) Kp = 0.541 (b) Kp = 3.42 (c) Kc = 281
15.27 Kc = 0.14
15.29 Pure solids and liquids are normally excluded from equilibrium-constant expressions because their concentrations, the ratio of moles of a substance to volume occupied by the substance, are constant.
15.31 (a) Kp = PO2 (b) Kc = [Hg(solv)]4[O2(solv)]
15.33 Kc = 10.5
15.35 (a) Kp = 51 (b) Kc = 2.1 × 103
15.37 (a) [H2] = 0.012 M, [N2] = 0.019 M, [H2O] = 0.138 M (b) Kc = 653.7 = 7 × 102
15.39 (a) PCO2 = 3.87 atm, PH2 = 1.82 atm, PCO = 0.23 atm (c) Kp = 0.11
15.41 Kc = 2.0 × 104
15.43 (a) A reaction quotient is the result of a general set of concentrations whereas the equilibrium constant requires equilibrium concentrations. (b) to the right (c) The concentrations used to calculate Q must be equilibrium concentrations.
15.45 (a) Q = 1.1 × 10–8, the reaction will proceed to the left. (b) Q = 5.5 × 10×12, the reaction will proceed to the right. (c) Q = 2.19 × 10–10, the mixture is at equilibrium.
15.47 PCl2 = 5.0 atm
15.49 (a) [Br2] = 0.00767 M, [Br] = 0.00282 M, 0.0451 g Br(g) (b) [H2] = 0.014M,[I2] = 0.00859 M, [HI] = 0.0081 M 21 g HI
15.51 [NO] = 0.002 M, [N2] = [O2] = 0.087 M
15.53 The equilibrium pressure of Br2(g) is 0.416 atm.
15.55 (a) [Ca2+] = [SO42–] = 4.9 × 10–3M (b) A bit more than 1.0 g CaSO4 is needed in order to have some undissolved CaSO4(s) in equilibrium with 1.4 L of saturated solution.
15.57 [IBr] = 0.223 M, [I2] = [Br2] = 0.0133 M
15.59 (a) PCH31 = PHI = 0.422 torr, PCH4 = 104.7 torr, PI2 = 7.54 torr
15.61 (a) Shift equilibrium to the right (b) decrease the value of K (c) shift equilibrium to the left (d) no effect (e) no effect (f) shift equilibrium to the right
15.63 (a) No effect (b) no effect (c) no effect (d) increase equilibrium constant (e) no effect
15.65 (a) ΔH° = –155.7 kJ (b) The reaction is exothermic, so the equilibrium constant will decrease with increasing temperature. (c) Δn does not equal zero, so a change in volume at constant temperature will affect the fraction of products in the equilibrium mixture.
15.67 An increase in pressure favors formation of ozone.
15.71 Kp = 24.7; Kc = 3.67 × 10–3
15.74 (a) PBr2 = 1.61 atm, PNO = 0.628 atm, PNOBr = 0.179 atm; Kc = 0.0643 (b) Pt = 0.968 atm (c) 10.49 g NOBr
15.77At equilibrium, PIBr = 0.21 atm, PI2 = PBr2 = 1.9 × 10–3 atm,
15.80 Kp = 4.33, Kc = 0.0480
15.83 [CO2] = [H2] = 0.264 M, [CO] = [H2O] = 0.236 M
15.87 (a) 26% of the CCl4 is converted to C and Cl2. (b) PCCl4 = 1.47 atm, PCl2 = 1.06 atm
15.91 Q = 8 × 10–6. Q > Kp, so the system is not at equilibrium; it will shift left to attain equilibrium. A catalyst that speeds up the reaction and thereby promotes the attainment of equilibrium would decrease the CO concentration in the exhaust.
15.93 At equilibrium, [H6IO4–] = 0.0015 M
15.97 850 °C, Kp = 14.1; at 950 °C, Kp = 73.8; at 1050 °C, Kp = 2.7 × 102; at 1200 °C, Kp = 1.7 × 103. Because K increases with increasing temperature, the reaction is endothermic.
CHAPTER 16
16.1 (a) HX, the H+ donor, is the Brønsted–Lowry acid. NH3, the H+ acceptor, is the Brønsted–Lowry base. (b) HX, the electron pair acceptor, is the Lewis acid. NH3, the electron pair donor, is the Lewis base.
16.3 (a) HY is a strong acid. There are no neutral HY molecules in solution, only H+ cations and Y– anions. (b) HX has the smallest Ka value. It has most neutral acid molecules and fewest ions. (c) HX has fewest H+ and highest pH.
16.5 (a) True. (b) False. Methyl orange turns yellow at a pH slightly greater than 4, so solution B could be at any pH greater than 4. (c) True.
16.7 (a) Molecule A, NH2OH (hydroxyl amine), acts as a base. Molecule A is an H+ acceptor because of the nonbonded electron pair on the N atom of the amine (— NH2) group, not because it contains an — OH group. (b) Molecule B, HCOOH (formic acid), acts as an acid. The molecule contains a — COOH group where the H atom bonded to O is ionizable and HCOOH is an H+ donor. (c) Molecule C, CH3OH (methanol), is an organic alcohol. The H atom bonded to O is not ionizable, and the — OH group does not dissociate in aqueous solution; it is neither an acid nor a base.
16.9 (a) Molecule (b) is more acidic because its conjugate base is resonance-stabilized and the ionization equilibrium favors the more stable products. (b) Increasing the electronegativity of X increases the strength of both acids. As X becomes more electronegative and attracts more electron density, the O — H bond becomes weaker, more polar, and more likely to be ionized. An electronegative X group also stabilizes the anionic conjugate base, causing the ionization equilibrium to favor products and the value of Ka to increase.
16.11 Solutions of HCl and H2SO4 conduct electricity, taste sour, turn litmus paper red (are acidic), neutralize solutions of bases, and react with active metals to form H2(g). HCl and H2SO4 solutions have these properties in common because both compounds are strong acids. That is, they both ionize completely in H2O to form H+ (aq) and an anion. (HSO4– is not completely ionized, but the first ionization step for H2SO4 is complete.) The presence of ions enables the solutions to conduct electricity; the presence of H+ (aq) in excess of 1 × 10–7M accounts for all other properties listed.
16.13 (a) The Arrhenius definition of an acid is confined to aqueous solution; the Brønsted–Lowry definition applies to any physical state. (b) HCl is the Brønsted–Lowry acid; NH3 is the Brønsted–Lowry base.
16.15 (a) (i) IO3– (ii) NH3 (b) (i) OH– (ii) H3PO4
16.17
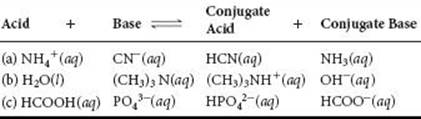
16.19 (a) Acid:
![]()
(b) H2C2O4 is the conjugate acid of HC2O4–. C2O42– is the conjugate base of HC2O4–.
16.21 (a) CH3COO–, weak base; CH3COOH, weak acid (b) HCO3–, weak base; H2CO3, weak acid (c) O2–, strong base; OH–, strong base (d) Cl–, negligible base; HCl, strong acid (e) NH3, weak base; NH4+, weak acid
16.23 (a) HBr. It is one of the seven strong acids. (b) F–. HCl is a stronger acid than HF, so F– is the stronger conjugate base.
16.25 (a) OH–(aq) + OH–(aq), the equilibrium lies to the right. (b) H2S(aq) + CH3COO–(aq), the equilibrium lies to the right. (c) HNO3(aq) + OH–(aq), the equilibrium lies to the left.
16.27 (a) No. In pure water, the only source of H+ is the autoionization reaction, which produces equal concentrations of H+ and OH–. As the temperature of water changes, the value of Kw changes, and the pH at which [H+] = [OH–] changes.
16.29 (a) [H+] = 2.2 × 10–11M, basic (b) [H+] = 1.1 × 10–6M, acidic (c) [H+] = 1.0 × 10–8M, basic
16.31 [H+] = [OH–] = 3.5 × 10–8M
16.33 (a) [H+] changes by a factor of 100. (b) [H+] changes by afactor of 3.2
16.35 (a) [H+] decreases, pH increases (b) The pH is between 3 and 4. By calculation, pH = 3.2; the solution is acidic. (c) pH = 5.2 is between pH 5 and pH 6, closer to pH = 5. A good estimate is 7 × 10–6M H+ and 3 × 10–9M OH–. By calculation, [H+] = 6 × 10–6M and [OH–] = 2 × 10–9M.
16.37
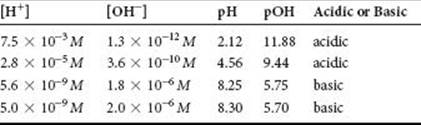
16.39 [H+] = 4.0 × 10–8M, [OH–] = 6.0 × 10–7M, pOH = 6.22
16.41 (a) A strong acid is completely ionized in aqueous solution. (b) [H+] = 0.500 M (c) HCl, HBr, HI
16.43 (a) [H+] = 8.5 × 10–3M, pH = 2.07 (b) [H+] = 0.0419 M, pH = 1.377 (c) [H+] = 0.0250 M, pH = 1.602 (d) [H+] = 0.167 M, pH = 0.778
16.45 (a) [OH–] = 3.0 × 10–3M, pH = 11.48 (b) [OH–] = 0.3758 M, pH = 13.5750 (c) [OH–] = 8.75 × 10–5M, pH = 9.942 (d) [OH–] = 0.17 M, pH = 13.23
16.47 3.2 × 10–3M NaOH
16.49 (a) HBrO2(aq) ![]() H+ (aq) + BrO2– (aq), Ka = [H+][BrO2–]/[HBrO2]; HBrO2(aq) + H2O(l)
H+ (aq) + BrO2– (aq), Ka = [H+][BrO2–]/[HBrO2]; HBrO2(aq) + H2O(l) ![]() H3O+(aq) + BrO2–(aq), Ka = [H3O+][BrO2–]/[HBrO2] (b) C2H5COOH(aq)
H3O+(aq) + BrO2–(aq), Ka = [H3O+][BrO2–]/[HBrO2] (b) C2H5COOH(aq) ![]() H+(aq) + C2H5COO–(aq) Ka = [H+][C2H5COO–]/[C2H5COOH]; C2H5COOH(aq) + H2O(l)
H+(aq) + C2H5COO–(aq) Ka = [H+][C2H5COO–]/[C2H5COOH]; C2H5COOH(aq) + H2O(l) ![]() H3O+(aq) + C2H5COO–(aq), Ka = [H3O+][C2H5COO–]/[C2H5COOH]
H3O+(aq) + C2H5COO–(aq), Ka = [H3O+][C2H5COO–]/[C2H5COOH]
16.51 Ka = 1.4 × 10–4
16.53 [H+] = [ClCH2COO–] = 0.0110 M, [ClCH2COOH] = 0.089 M, Ka = 1.4 × 10–3
16.55 0.089 M CH3COOH
16.57 [H+] = [C6H5COO–] = 1.8 × 10–3M, [C6H5COOH] = 0.048 M
16.59 (a) [H+] = 1.1 × 10–3M, pH = 2.95 (b) [H+] = 1.7 × 10–4M, pH = 3.76 (c) [OH–] = 1.4 × 10–5M, pH = 9.15
16.61 [H+] = 2.0 × 10–2M, pH = 1.71
16.63 (a) [H+] = 2.8 × 10–3M, 0.69% ionization (b) [H+] = 1.4 × 10–3M, 1.4% ionization (c) [H+] = 8.7 × 10–4M, 2.2% ionization
16.65 HX(aq) ![]() H+(aq) + X–(aq); Ka = [H+][X–]/[HX]. Assume that the percent of acid that ionizes is small. Let [H+] = [X–] = y, Ka = y2/[HX]; y = Ka1/2[HX]1/2. Percent ionization = y/[HX] × 100. Substituting for y, percent ionization = 100 Ka1/2[HX]1/2/[HX] or 100 Ka1/2/[HX]1/2. That is, percent ionization varies inversely as the square root of the concentration of HX.
H+(aq) + X–(aq); Ka = [H+][X–]/[HX]. Assume that the percent of acid that ionizes is small. Let [H+] = [X–] = y, Ka = y2/[HX]; y = Ka1/2[HX]1/2. Percent ionization = y/[HX] × 100. Substituting for y, percent ionization = 100 Ka1/2[HX]1/2/[HX] or 100 Ka1/2/[HX]1/2. That is, percent ionization varies inversely as the square root of the concentration of HX.
16.67 [H+] = 5.1 × 10–3M, pH = 2.29, [C6H5O73–] = 1.3 × 10–9M. The approximation that the first ionization is less than 5% of the total acid concentration is not valid; the quadratic equation must be solved. The [H+] produced from the second and third ionizations is small with respect to that present from the first step; the second and third ionizations can be neglected when calculating the [H+] and pH. [C6H5O73–] is much less than [H+].
16.69 (a) HONH3+ (b) When hydroxylamine acts as a base, the nitrogen atom accepts a proton. (c) In hydroxylamine, O and N are the atoms with nonbonding electron pairs; in the neutral molecule both have zero formal charges. Nitrogen is less electronegative than oxygen and more likely to share a lone pair of electrons with an incoming (and electron-deficient) H+. The resulting cation with the formal charge on N is more stable than the one with the +1 formal charge on O.
16.71 (a) (CH3)2NH(aq) + H2O(l) ![]() (CH3)2NH2+(aq) + OH–(aq); Kb = [(CH3)2NH2+][OH–]/[(CH3)2NH] (b) CO32–(aq) + H2O(l)
(CH3)2NH2+(aq) + OH–(aq); Kb = [(CH3)2NH2+][OH–]/[(CH3)2NH] (b) CO32–(aq) + H2O(l) ![]() HCO3–(aq) + OH–(aq); Kb = [HCO3–][OH–]/[(CO32–)] (c) HCOO–(aq) + H2O(l)
HCO3–(aq) + OH–(aq); Kb = [HCO3–][OH–]/[(CO32–)] (c) HCOO–(aq) + H2O(l) ![]() HOOOH(aq) + OH–(aq) Kb = [HCOOH][OH–]/[HCOO–]
HOOOH(aq) + OH–(aq) Kb = [HCOOH][OH–]/[HCOO–]
16.73 From the quadratic formula, [OH–] = 6.6 × 10–3M, pH = 11.82.
16.75 (a) [C10H15ON] = 0.033 M, [C10H15ONH+] = [OH–] = 2.1 × 10–3M (b) Kb = 1.4 × 10–4
16.77 (a) For a conjugate acid/conjugate base pair such as C6H5OH/C6H5O–, Kb for the conjugate base can always be calculated from for the conjugate acid, so a separate list of Kb values is not necessary. (b) Kb = 7.7 × 10–5 (c) Phenolate is a stronger base than NH3.
16.79 (a) Acetic acid is stronger. (b) Hypochlorite ion is the stronger base. (c) For CH3COO–, Kb = 5.6 × 10–10; for CIO–, Kb = 3.3 × 10–7.
16.81 (a) [OH–] = 6.3 × 10–4M, pH = 10.80 (b) [OH–] = 9.2 × 10–5M, pH = 9.96 (c) [OH–] = 3.3 × 10–6M, pH = 8.52
16.83 (a) Acidic (b) acidic (c) basic (d) neutral (e) acidic
16.85 Kb for the anion of the unknown salt is 1.4 × 10–11; Kb for the conjugate acid is 7.1 × 10–4. The conjugate acid is HF and the salt is NaF.
16.87 (a) As the electronegativity of the central atom (X) increases, the strength of the oxyacid increases. (b) As the number of nonprotonated oxygen atoms in the molecule increases, the strength of the oxyacid increases.
16.89 (a) HNO3 is a stronger acid because it has one more nonprotonated oxygen atom and thus a higher oxidation number on N. (b) For binary hydrides, acid strength increases going down a family, so H2S is a stronger acid than H2O. (c) H2SO4 is a stronger acid because H+ is much more tightly held by the anion HSO4–. (d) For oxyacids, the greater the electronegativity of the central atom, the stronger the acid, so H2SO4 is the stronger acid. (e) CCl3COOH is stronger because the electronegative Cl atoms withdraw electron density from other parts of the molecule, which weakens the O — H bond and stabilizes the anionic conjugate base. Both effects favor increased ionization and acid strength.
16.91 (a) BrO– (b) BrO– (c) HPO42–
16.93 (a) True (b) False. In a series of acids that have the same central atom, acid strength increases with the number of nonprotonated oxygen atoms bonded to the central atom. (c) False. H2Te is a stronger acid than H2S because the H — Te bond is longer, weaker, and more easily ionized than the H — S bond.
16.95 Yes. The Arrhenius definition of a base, an OH–(aq) donor, is most restrictive; the Brønsted definition, an H+ acceptor, is more general; and the Lewis definition, an electron-pair donor, is most general. Any substance that fits the narrow Arrhenius definition will fit the broader Brønsted and Lewis definitions.
16.97 (a) Acid, Fe(ClO4)3 or Fe3+; base, H2O (b) Acid, H2O; base, CN– (c) Acid, BF3; base, (CH3)3N (d) Acid, HIO; base, NH2–
16.99 (a) Cu2+, higher cation charge (b) Fe3+, higher cation charge (c) Al3+, smaller cation radius, same charge
16.101 (C2H5)3N is a stronger base than NH3 by virture of its smaller pKb.
16.104 K = 3.3 × 107
16.107 (a) For solutions with equal concentrations, the weaker acid will have a lower [H+] and higher pH. (b) The acid with Ka = 8 × 10–5 is the weaker acid, so it has the higher pH. (c) The base with pKb = 4.5 is the stronger base, has the greater [OH–] and smaller [H+], so higher pH.
16.109 Ka = 1.4 × 10–5
16.115 6.0 × 1013 H+ ions
16.118 (a) To the precision of the reported data, the pH of rainwater 40 years ago was 5.4, no different from the pH today. With extra significant figures, [H+] = 3.61 × 10–6M, pH = 5.443 (b) A 20.0-L bucket of today's rainwater contains 0.02 L (with extra significant figures, 0.0200 L) of dissolved CO2.
16.119 (a) 
The electron-domain geometry and molecular structure are trigonal planar. (b) The Al atom is electron deficient. It acts like a Lewis acid in order to complete its octet.
(c) 
(d) The Lewis theory is most appropriate. H+ and AlCl3 are both electron pair acceptors.
16.121 Rx 1, ΔH = 104 kJ; Rx 2, ΔH = – 32kJ. Reaction 2 is exothermic while reaction 1 is endothesmic. For binary acids with heavy atoms (X) in the same family, the longer and weaker the H — X bond, the stronger the acid (and the more exothermic the ionization reaction).
16.124 (a) K(i) = 5.6 × 103, K(ii) = 10 (b) Both (i) and (ii) have K > 1, so both could be written with a single arrow.
CHAPTER 17
17.1 The middle box has the highest pH. For equal amounts of acid HX, the greater the amount of conjugate base X–, the smaller the amount of H+ and the higher the pH.
17.4 (a) Drawing 3 (b) Drawing 1 (c) Drawing 2
17.7 (a) The red curve corresponds to the more concentrated acid solution. (b) On the titration curve of a weak acid, pH = pKa at the volume halfway to the equivalence point. At this volume, the red curve has the smaller pKa and the larger Ka.
17.10 (a) Q = 4.67 × 10–6; Q < Ksp and the solution is not saturated. (b) Ca(OH)2 precipitate forms in beaker (iii).
17.13 (a) The extent of ionization of a weak electrolyte is decreased when a strong electrolyte containing an ion in common with the weak electrolyte is added to it. (b) NaNO2
17.15 (a) [H+] = 1.8 × 10–5M, pH = 4.73 (b) [OH–] = 4.8 × 10–5M, pH = 9.68 (c) [H+] = 1.4 × 10–5M, pH = 4.87
17.17 (a) 4.5% ionization (b) 0.018% ionization
17.19 In a mixture of CH3COOH and CH3COONa, CH3COOH reacts with added base and CH3COO– combines with added acid, leaving [H+] relatively unchanged. Although HCl and Cl– are a conjugate acid–base pair, Cl– has no tendency to combine with added acid to form undissociated HCl. Any added acid simply increases [H+] in an HCl — NaCl mixture.
17.21 (a) pH = 3.82 (b) pH = 3.96
17.23 (a) pH = 5.26
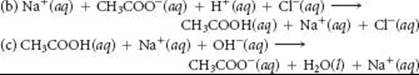
17.25 (a) pH = 1.58 (b) 36 g NaF
17.27 (a) pH = 4.86 (b) pH = 5.0 (c) pH = 4.71
17.29 (a) [HCO3–]/[H2CO3] = 11 (b) [HCO3–]/[H2CO3] = 5.4
17.31 360 mL of 0.10 M HCOONa, 640 mL of 0.10 M HCOOH
17.33 (a) Curve B (b) pH at the approximate equivalence point of curve A = 8.0, pH at the approximate equivalence point of curve B = 7.0 (c) For equal volumes of A and B, the concentration of acid B is greater, since it requires a larger volume of base to reach the equivalence point.
17.35 (a) False (b) true (c) true
17.37 (a) Above pH 7 (b) below pH 7 (c) at pH 7
17.39 The second color change of Thymol blue is in the correct pH range to show the equivalence point of the titration of a weak acid with a strong base.
17.41 (a) 42.4 mL NaOH soln (b) 35.0 mL NaOH soln (c) 29.8 mL NaOH soln
17.43 (a) pH = 1.54 (b) pH = 3.30 (c) pH = 7.00 (d) pH = 10.69 (e) pH = 12.74
17.45 (a) pH = 2.78 (b) pH = 4.74 (c) pH = 6.58 (d) pH = 8.81 (e) pH = 11.03 (f) pH = 12.42
17.47 (a) pH = 7.00 (b) [HONH3+] = 0.100 M, pH = 3.52 (c) [C6H5NH3+] = 0.100 M, pH = 2.82
17.49 (a) The concentration of undissolved solid does not appear in the solubility product expression because it is constant. (b) Ksp = [Ag+][I–]; Ksp = [Sr2+][SO42–]; Ksp = [Fe2+] [OH–]2; Ksp = [Hg22+][Br–]2
17.51 (a) Ksp = 7.63 × 10–9 (b) Ksp = 2.7 × 10–9 (c) 5.3 × 10–4 molBa(IO3)2/L
17.53 Ksp = 2.3 × 10–9
17.55 (a) 7.1 × 10–7 mol AgBr/L (b) 1.7 × 10–11 mol AgBr/L (c) 5.0 × 10–12 mol AgBr/L
17.57 (a) The amount of CaF2(s) on the bottom of the beaker increases. (b) The [Ca2+] in solution increases. (c) The [F–] in solution decreases.
17.59 (a) 1.4 × 103 gMn(OH)2/L (b) 0.014 g/L (c) 3.6 × 10–7 g/L
17.61 More soluble in acid: (a) ZnCO3 (b) ZnS (d) AgCN (e) Ba3(PO4)2
17.63 [Ni2+] = 1 × 10–8M
17.65 (a) 9.1 × 10–9 mol AgI/L pure water (b) K = Ksp × Kf = 8 × 104 (c) 0.0500 mol AgI/L 0.100 M NaCN
17.67 (a) Q < Ksp; no Ca(OH)2 precipitates (b) Q < Ksp; no Ag2SO4 precipitates
17.69 pH = 11.5
17.71 AgI will precipitate first, at [I–] = 4.2 × 10–13M.
17.73 AgCl will precipitate first.
17.75 The first two experiments eliminate group 1 and 2 ions (Figure 17.23). The absence of insoluble phosphate precipitates in the filtrate from the third experiment rules out group 4 ions. The ions that might be in the sample are those from group 3, Al3+, Fe3+, Cr3+, Zn2+, Ni2+, Mn2+, or Co2+, and from group 5, NH4+, Na+, or K+.
17.77 (a) Make the solution acidic with 0.2 M HCl; saturate with H2S. CdS will precipitate; ZnS will not. (b) Add excess base; Fe(OH3)(s) precipitates, but Cr3+ forms the soluble complex Cr(OH)4–. (c) Add (NH4)2HPO4; Mg2+ precipitates as MgNH4PO4; K+ remains soluble. (d) Add 6 MHCl; precipitate as Ag+ as AgCl(s); Mn2+ remains soluble.
17.79 (a) Base is required to increase [PO43–] so that the solubility product of the metal phosphates of interest is exceeded and the phosphate salts precipitate. (b) Ksp for the cations in group 3 is much larger, and so to exceed Ksp, a higher [S2–] is required. (c) They should all redissolve in strongly acidic solution.
17.81 pOH = pKb + log{|BH–|/|B|}
17.83 (a) pH = 3.171 (b) pH = 2.938 (c) pH = 12.862
17.86 (a) pH of buffer A = pH of buffer B = 3.74. For buffers containing the same conjugate acid and base components, the pH is determined by the ratio of concentrations of conjugate acid and base. Buffers A and B have the same ratio of concentrations, so their pH values are equal. (b) Buffer capacity is determined by the absolute amount of buffer components available to absorb strong acid or strong base. Buffer A has the greater capacity because it contains the greater absolute concentrations of HCOOH and HCOO–. (c) Buffer A: pH = 3.74, ΔpH = 0.00; buffer B: pH = 3.66, ΔpH = –0.12 (d) Buffer A: pH = 3.74, ΔpH = 0.00; buffer B: pH = 2.74, ΔpH = –1.00 (e) The results of parts (c) and (d) are quantitative confirmation that buffer A has a significantly greater capacity than buffer B.
17.88 (a) molar mass = 82.2 g/mol (b) Ka = 3.8 × 10–7
17.90 At the halfway point, molHA = molA– and [HA] = [A–].
![]()
log(1) = 0 and pH = pKa of the weak acid being titrated.
17.92 pH = 7.75
17.93 1.6 L of 1.0 M NaOH
17.96 (a) CdS (b) BaCrO4 (c) NiCo3 (d) Ag2SO4
17.100 The solubility of Mg(OH)2 in 0.50 M NH4Cl is 0.11 mol/L
17.101 [KMnO4] = [MnO4–] = 0.11 M
17.104 [OH–] = 1.7 × 10–11M, pH of the buffer = 3.22
17.107 (a) The molar solubility of Cd(OH)2 is 1.8 × 10–5 mol/L. (b) The initial concentration of NaBr required to increase the molar solubility of Cd(OH)2 to 1.0 × 10–3 mol/L is 2 M.
17.108 (a) H+(aq) + HCOO–(aq) ![]() HCOOH(aq) (b) K = 5.6 × 103 (c) [Na+] = [Cl–] = 0.075 M, [H+] = [HCOO–] = 3.7 × 10–3M, [HCOOH] = 0.071 M
HCOOH(aq) (b) K = 5.6 × 103 (c) [Na+] = [Cl–] = 0.075 M, [H+] = [HCOO–] = 3.7 × 10–3M, [HCOOH] = 0.071 M
17.114 [Sr2+] = [SO42–] = 5.7 × 10–4M, Ksp = 3.2 × 10–7
CHAPTER 18
18.1 (a) A greater volume than 22.4 L (b) The gas will occupy more volume at 85 km than at 50 km. (c) We expect gases to behave most ideally in the thermosphere, around the stratopause and in the troposphere at low altitude.
18.6 Salt water contains high concentrations of dissolved salts and solids. It includes the world ocean (97.2% of all water, approximately 35,000 ppm of dissolved salts) and brackish or salty water (0.1% of all water). Freshwater (0.6% of all water on earth) refers to natural waters that have low concentrations (less than 500 ppm) of dissolved salts and solids. It includes the waters of lakes, rivers, ponds, and streams. Groundwater is freshwater that is under the soil. It resides in aquifers, porous rock that holds water, and composes 20% of the world's freshwater.
18.9 The basic goals of green chemistry are to minimize or eliminate solvents and waste, generate nontoxic waste, be energy efficient, employ renewable starting materials, and take advantage of catalysts that enable the use of safe and common reagents.
18.11 (a) Its temperature profile (b) troposphere, 0 to 12 km; stratosphere, 12 to 50 km; mesosphere, 50 to 85 km; thermosphere, 85 to 110 km
18.13 (a) The partial pressure of O3 is 3.0 × 10–7 atm (2.2 × 10–4 torr). (b) 7.3 × 1015 O3 molecules/1.0 L air
18.15 8.6 × 1016 CO molecules/1.0 L air
18.17 (a) 570 nm (b) visible electromagnetic radiation
18.19 (a) Photodissociation is cleavage of a bond such that two neutral species are produced. Photoionization is absorption of a photon with sufficient energy to eject an electron, producing an ion and the ejected electron. (b) Photoionization of O2 requires 1205 kJ/mol. Photodissociation requires only 495 kJ/mol. At lower elevations, high-energy short-wavelength solar radiation has already been absorbed. Below 90 km, the increased concentration of O2 and the availability of longer-wavelength radiation cause the photodissociation process to dominate.
18.21 Ozone depletion reactions, which involve only O3, O2, or O (oxidation state = 0), do not involve a change in oxidation state for oxygen atoms. Reactions involving ClO and one of the oxygen species with a zero oxidation state do involve a change in the oxidation state of oxygen atoms.
18.23 (a) A chloro-fluorocarbon is a compound that contains chlorine, fluorine, and carbon, while a hydrofluorocarbon is a compound that contains hydrogen, fluorine, and carbon. An HFC contains hydrogen in place of the chlorine present in a CFC. (b) HFCs are potentially less harmful than CFCs because their photodissociation does not produce Cl atoms, which catalyze the destruction of ozone.
18.25 (a) The C — F bond requires more energy for dissociation than the C — Cl bond and is not readily cleaved by the available wavelengths of UV light. (b) Chlorine is present as chlorine atoms and chlorine oxide molecules, Cl and ClO, respectively.
18.27 (a) Methane, CH4, arises from decomposition of organic matter by certain microorganisms; it also escapes from underground gas deposits. (b) SO2 is released in volcanic gases and also is produced by bacterial action on decomposing vegetable and animal matter. (c) Nitric oxide, NO, results from oxidation of decomposing organic matter and is formed in lightning flashes.
18.29 (a) H2SO4(aq) + CaCO3(s) ![]() CaSO4(s) + H2O(l) + CO2(g) (b) The CaSO4(s) would be much less reactive with acidic solution, since it would require a strongly acidic solution to shift the relevant equilibrium to the right: CaSO4(s) + 2H+(aq)
CaSO4(s) + H2O(l) + CO2(g) (b) The CaSO4(s) would be much less reactive with acidic solution, since it would require a strongly acidic solution to shift the relevant equilibrium to the right: CaSO4(s) + 2H+(aq) ![]() Ca2+(aq) + 2HSO4–(aq). CaSO4would protect CaC03 from attack by acid rain, but it would not provide the structural strength of limestone.
Ca2+(aq) + 2HSO4–(aq). CaSO4would protect CaC03 from attack by acid rain, but it would not provide the structural strength of limestone.
18.31 (a) Ultraviolet (b) 357 kJ/mol (c) The average C — H bond energy from Table 8.4 is 413 kJ/mol. The C — H bond energy in CH2O, 357 kJ/mol, is less than the “average” C — H bond energy.
(d) ![]()
18.33 Incoming and outgoing energies are in different regions of the electromagnetic spectrum. CO2 is transparent to incoming visible radiation but absorbs outgoing infrared radiation.
18.35 0.099 M Na+
18.37 (a) 3.22 × 103 gH2O (b) The final temperature is 43.4 °C.
18.39 4.361 × 105 g CaO
18.41 (a) Groundwater is freshwater (less than 500 ppm total salt content) that is under the soil; it composes 20% of the world's freshwater. (b) An aquifer is a layer of porous rock that holds groundwater.
18.43 The minimum pressure required to initiate reverse osmosis is greater than 5.1 atm.
18.45 (a) CO2(g), HCO3–, H2O(l), SO42–, NO3–, HPO42–, H2PO4– (b) CH4(g), H2S(g), NH3(g), PH3(g)
18.47 25.1 g O2
18.49 Mg2+(aq) + Ca(OH)2(s) ![]() Mg(OH)2(s) + Ca2+(aq)
Mg(OH)2(s) + Ca2+(aq)
18.51 0.42 mol Ca(OH)2, 0.18 mol Na2CO3
18.53 4 FeSO4(aq) + O2(aq) + 2H2O(l) ![]() 4Fe3+(aq) + 4OH–(aq) + 4SO42–(aq); Fe3+(aq) + 3HCO3–(aq)
4Fe3+(aq) + 4OH–(aq) + 4SO42–(aq); Fe3+(aq) + 3HCO3–(aq) ![]() Fe(OH)3(s) + 3CO2(g)
Fe(OH)3(s) + 3CO2(g)
18.55 (a) Trihalomethanes are the by-products of water chlorination; they contain one central carbon atom bound to one hydrogen and three halogen atoms.
(b) 
18.57 The fewer steps in a process, the less waste is generated. Processes with fewer steps require less energy at the site of the process and for subsequent cleanup or disposal of waste.
18.59 (a) H2O (b) It is better to prevent waste than to treat it. Atom economy. Less hazardous chemical synthesis and inherently safer for accident prevention. Catalysis and design for energy efficiency. Raw materials should be renewable.
18.61 (a) Water as a solvent, by criteria 5, 7, and 12. (b) Reaction temperature of 500 K, by criteria 6, 12, and 1. (c) Sodium chloride as a by-product, according to criteria 1, 3, and 12.
18.66 Multiply Equation 18.7 by a factor of 2; then add it to Equation 18.9. 2 Cl(g) and 2 ClO(g) cancel from each side of the resulting equation to produce Equation 18.10.
18.69 Although HFCs have long lifetimes in the stratosphere, it is infrequent that light with energy sufficient to dissociate a C — F bond will reach an HFC molecule. F atoms, the bad actors in ozone destruction, are much less likely than Cl atoms to be produced by photodissociation in the stratosphere.
18.71 The formation of NO(g) is endothermic, so K increases with increasing temperature. The oxidation of NO(g) to NO2(g) is exothermic, so the value of K decreases with increasing temperature.
18.75 7.1 × 108m2
18.77 (a) CO32– is a relatively strong Brønsted–Lowry base and produces OH– in aqueous solution. If [OH–(aq)] is sufficient for the reaction quotient to exceed Ksp for Mg(OH)2, the solid will precipitate. (b) At these ion concentrations, Q > Ksp and Mg(OH)2 will precipitate.
18.81 (a) 2.5 × 10 ton CO2, 4.2 × 105 ton SO2(b) 4.3 × 105 ton CaSO3
18.84 (a)
![]()
(b) 258 nm (c) The overall reaction is O3(g) + O(g) ![]() 2 O2(g). OH(g) is the catalyst in the overall reaction because it is consumed and then reproduced.
2 O2(g). OH(g) is the catalyst in the overall reaction because it is consumed and then reproduced.
18.86 The enthalpy change for the first step is –141 kJ, for the second step, –249 kJ, for the overall reaction, –390kJ.
18.90 (a) Rate = k[O3][H] (b) kavg 1.13 × 1044M–1s–1
18.95 (a) Process (i) is greener because it involves neither the toxic reactant phosgene nor the by-product HCl. (b) Reaction (i): C in CO2 is linear with sp hybridization; C in R — N ═ C ═ O is linear with sp hybridization; C in the urethane monomer is trigonal planar with sp2 hybridization. Reaction (ii): C in COCl2 is linear with sp2 hybridization; C in R — N ═ C ═ O is linear with sp hybridization; C in the urethane monomer is trigonal planar with sp2 hybridization. (c) The greenest way to promote formation of the isocyanate is to remove by–product, either water or HCl, from the reaction mixture.
CHAPTER 19
19.1 (a)

(b) ΔH = 0 for mixing ideal gases. ΔS is positive because the disorder of the system increases. (c) The process is spontaneous and therefore irreversible. (d) Since ΔH = 0, the process does not affect the entropy of the surroundings.
19.4 ΔS is positive.
19.7 (a) At 300 K, ΔG = 0, and the system is at equilibrium. (b) The reaction is spontaneous at temperatures above 300 K.
19.10 (a) The minimum in the plot is the equilibrium position of the reaction. (b) The quantity x is ΔG°.
19.11 Spontaneous: a, b, c, d; nonspontaneous: e
19.13 (a) NH4NO3(s) dissolves in water, as in a chemical cold pack. Naphthalene (moth balls) sublimes at room temperature. (b) Melting of a solid is spontaneous above its melting point but nonspontaneous below its melting point.
19.15 (a) Endothermic (b) above 100 °C (c) below 100 °C (d) at 100 °C
19.17 (a) For a reversible process, the forward and reverse changes occur by the same path. In a reversible process, both the system and the surroundings are restored to their original condition by exactly reversing the change. A reversible change produces the maximum amount of work. (b) There is no net change in the surroundings. (c) The vaporization of water to steam is reversible if it occurs at the boiling temperature of water for a specified external (atmospheric) pressure and if the required heat is added infinitely slowly. (d) No. Natural processes are spontaneous in the direction they occur and nonspontaneous in the opposite direction. By definition they are irreversible.
19.19 (a) If the ideal gas is contained in a closed system at constant volume, a decrease in external temperature leads to a decrease in both temperature and pressure of the gas. (b) If the ideal gas is contained in a closed system at constant pressure, a decrease in external temperature leads to a decrease in both temperature and volume of the gas. (c) No. ΔE is a state function. ΔE = q + w; q and w are not state functions. Their values do depend on path, but their sum, ΔE, does not.
19.21 (a) An ice cube can melt reversibly at the conditions of temperature and pressure where the solid and liquid are in equilibrium. (b) We know that melting is a process that increases the energy of the system even though there is no change in temperature. ΔE is not zero for the process.
19.23 (a) At constant temperature, ΔS = qrev/T, where qrev is the heat that would be transferred if the process were reversible. (b) No. ΔS is a state function, so it is independent of path.
19.25 (a) Entropy increases. (b) 89.2 J/K
19.27 (a) For a spontaneous process, the entropy of the universe increases; for a reversible process, the entropy of the universe does not change. (b) For a reversible process, if the entropy of the system increases, the entropy of the surroundings must decrease by the same amount. (c) For a spontaneous process, the entropy of the universe must increase, so the entropy of the surroundings must decrease by less than 42 J/K.
19.29 (a) Positive ΔS (b) ΔS = 1.02 J/K (c) Temperature need not be specified to calculate ΔS, as long as the expansion is isothermal.
19.31 (a) Yes, the expansion is spontaneous. (b) As the ideal gas expands into the vacuum, there is nothing for it to “push back,” so no work is done. Mathematically, w = –PextΔV. Since the gas expands into a vacuum, Pext = 0 and w = 0. (c) The “driving force” for the expansion of the gas is the increase in entropy.
19.33 (a) An increase in temperature produces more available microstates for a system. (b) A decrease in volume produces fewer available microstates for a system. (c) Going from liquid to gas, the number of available microstates increases.
19.35 (a) ΔS is positive. (b) S of the system clearly increases in 19.11 (b) and (e); it clearly decreases in 19.9 (c). The entropy change is difficult to judge in 19.9 (a) and definition of the system in (d) is problematic.
19.37 S increases in (a) and (c); S decreases in (b).
19.39 (a) The entropy of a pure crystalline substance at absolute zero is zero. (b) In translational motion the entire molecule moves in a single direction; in rotational motion the molecule rotates or spins around a fixed axis. In vibrational motion the bonds within a molecule stretch and bend, but the average position of the atoms does not change.
19.41 (a) Ar(g) (b) He(g) at 1.5 atm (c) 1 mol of Ne(g) in 15.0 L (d) CO2(g)
19.43 (a) ΔS < 0 (b) ΔS > 0 (c) ΔS < 0 (d) ΔS ≈ 0
19.45 (a)
(b) Boiling water, at 100°C, has a much larger entropy change than melting ice at 0 °C.
19.47 (a) C2H6(g) (b) CO2(g)
19.49 (a) Sc(s), 34.6 J/mol-K; Sc(g), 174.7 J/mol-K. In general, the gas phase of a substance has a larger S° than the solid phase because of the greater volume and motional freedom of the molecules. (b) NH3(g), 192.5 J/mol-K; NH3(aq), 111.3 J/mol-K. Molecules in the gas phase have more motional freedom than molecules in solution. (c) 1 mol of P4(g), 280 J/K; 2 mol of P2(g), 2(218.1) = 436.2 J/K. More particles have a greater motional energy (more available microstates). (d) C (diamond), 2.43 J/mol-K; C (graphite), 5.69 J/mol-K. The internal entropy in graphite is greater because there is translational freedom among planar sheets of C atoms, while there is very little freedom within the covalent-network diamond lattice.
19.51 For elements with similar structures, the heavier the atoms, the lower the vibrational frequencies at a given temperature. This means that more vibrations can be accessed at a particular temperature, resulting in greater absolute entropy for the heavier elements.
19.53 (a) ΔS° = –120.5 J/K. ΔS° is negative because there are fewer moles of gas in the products. (b) ΔS° = +176.6 J/K. ΔS° is positive because there are more moles of gas in the products. (c) ΔS° = +152.39 J/K. ΔS° is positive because the product contains more total particles and more moles of gas. (d) ΔS° = +92.3 J/K. ΔS° is positive because there are more moles of gas in the products.
19.55 (a) ΔG = ΔH – TΔS (b) If ΔG is positive, the process is nonspontaneous, but the reverse process is spontaneous. (c) There is no relationship between ΔG and rate of reaction.
19.57(a) Exothermic (b) ΔS° is negative; the reaction leads to a decrease in disorder. (c) ΔG° = –9.9 kJ (d) If all reactants and products are present in their standard states, the reaction is spontaneous in the forward direction at this temperature.
19.59 (a) ΔH° = –537.22 kJ, ΔS° = 13.7 J/K, ΔG° = –541.40 kJ, ΔG° = ΔH° – TΔS ° = –541.31 kJ (b) ΔH° = –106.7kJ, ΔS° = –142.2 kJ, ΔG° = –64.0 kJ, ΔG° = ΔH° – TΔS ° = –64.3 kJ (c) ΔH° = –508.3 kJ, ΔS° = –178 kJ, ΔG° = –465.8 kJ, ΔG° = ΔH° – TΔS ° = –455.1 kJ. The discrepancy in ΔG° values is due to experimental uncertainties in the tabulated thermodynamic data. (d) ΔH° = –165.9 kJ, ΔS° = 1.4 kJ, ΔG° = –166.2 kJ, ΔG° = ΔH° – TΔS ° = –166.3 kJ
19.61 (a) ΔG° = –140.0 kJ, spontaneous (b) ΔG° = +104.70 kJ, nonspontaneous (c) ΔG° = +146 kJ, nonspontaneous (d) ΔG° = –156.7 kJ, spontaneous
19.63 (a) 2C8H18(l) + 25O2(g) ![]() 16 CO2(g) + 18 H2O(l) (b) Because ΔS° is positive, ΔG° is more negative than ΔH°.
16 CO2(g) + 18 H2O(l) (b) Because ΔS° is positive, ΔG° is more negative than ΔH°.
19.65 (a) The forward reaction is spontaneous at low temperatures but becomes nonspontaneous at higher temperatures. (b) The reaction is nonspontaneous in the forward direction at all temperatures. (c) The forward reaction is nonspontaneous at low temperatures but becomes spontaneous at higher temperatures.
19.67 ΔS > 60.8J/K
19.69 (a) T = 330K (b) nonspontaneous
19.71 (a) ΔH° = 155.7 kJ, ΔS° = 171.4 kJ. Since ΔS° is positive, ΔG° becomes more negative with increasing temperature. (b) ΔG° = 19 kJ. The reaction is not spontaneous under standard conditions at 800 K (c) ΔG° = –15.7 kJ. The reaction is spontaneous under standard conditions at 1000 K.
19.73 (a) Tb = 79 °C (b) From the Handbook of Chemistry and Physics, 74th Edition, Tb = 80.1 °C. The values are remarkably close; the small difference is due to deviation from ideal behavior by C6H6(g) and experimental uncertainty in the boiling point measurement and the thermodynamic data.
19.75 (a) ![]() (b) –1299.5 kJ of heat produced/mol C2H2 burned (c) wmax = –1235.1 kJ/mol C2H2
(b) –1299.5 kJ of heat produced/mol C2H2 burned (c) wmax = –1235.1 kJ/mol C2H2
19.77 (a) ΔG becomes more negative. (b) ΔG becomes more positive. (c) ΔG becomes more positive.
19.79 (a) ΔG° = –5.40 kJ (b) ΔG = 0.30 kJ
19.81 (a) ΔG° = –16.77 kJ, K = 870 (b) ΔG° = 8.0 kJ, K = 0.039 (c) ΔG° = –497.9 kJ, K = 2 × 1087
19.83 ΔH° = 269.3 kJ, ΔS° = 0.1719 kJ/K (a) PCO2 = 6.0 × 10–39atm (b) PCO2 = 1.6 × 10–4atm
19.85 (a) HNO2(aq) ![]() H+(aq) + NO2–(aq) (b) ΔG° = 19.1kJ (c) ΔG = 0 at equilibrium (d) ΔG = –2.7 kJ
H+(aq) + NO2–(aq) (b) ΔG° = 19.1kJ (c) ΔG = 0 at equilibrium (d) ΔG = –2.7 kJ
19.87 (a) The thermodynamic quantities T, E, and S are state functions. (b) The quantities q and w depend on the path taken. (c) There is only one reversible path between states. (d) ΔE = qrev + wmax, ΔS = qrev/T.
19.91 (a) 16 arrangements (b) 1 arrangement (c) The gas will spontaneously adopt the state with the most possible arrangements for the molecules, the state with maximum disorder.
19.96 (a) For all three compounds listed, there are fewer moles of gaseous products than reactants in the formation reaction, so we expect ![]() to be negative. If
to be negative. If ![]() =
= ![]() –
– ![]() and
and ![]() is negative, –
is negative, – ![]() is positive and
is positive and ![]() is more positive than
is more positive than ![]() . (b) In this reaction, there re more moles of gas in products,
. (b) In this reaction, there re more moles of gas in products, ![]() is positive, –
is positive, –![]() is negative and
is negative and ![]() is more negative than
is more negative than ![]() .
.
19.100 (a) K = 4 × 1015 (b) An increase in temperature will decrease the mole fraction of CH3COOH at equilibrium. Elevated temperatures must be used to increase the speed of the reaction. (c) K = 1 at 836 K or 563 °C.
19.104 (a) ΔG = 8.77 kJ (b) wmin = 8.77 kJ. In practice, a larger than minimum amount of work is required.
19.108 (a) Acetone, ![]() dimethyl ether,
dimethyl ether, ![]() ethanol,
ethanol, ![]() octane,
octane, ![]() pyridine,
pyridine, ![]() Ethanol does not obey Troutons rule. (b) Hydrogen bonding (in ethanol and other liquids) leads to more ordering in the liquid state and a greater than usual increase in entropy upon vaporization. Liquids that experience hydrogen bonding are probably exceptions to Troutons rule. (c) Owing to strong hydrogen bonding interactions, water probably does not obey Troutons rule.
Ethanol does not obey Troutons rule. (b) Hydrogen bonding (in ethanol and other liquids) leads to more ordering in the liquid state and a greater than usual increase in entropy upon vaporization. Liquids that experience hydrogen bonding are probably exceptions to Troutons rule. (c) Owing to strong hydrogen bonding interactions, water probably does not obey Troutons rule. ![]() (d) ΔHvap for C6H5Cl ≈ 36 kJ/mol
(d) ΔHvap for C6H5Cl ≈ 36 kJ/mol
19.113 (a) For any given total pressure, the condition of equal moles of the two gases can be achieved at some temperature. For individual gas pressures of 1 atm and a total pressure of 2 atm, the mixture is at equilibrium at 328.5 K or 55.5 °C. (b) 333.0 K or 60 °C (c) 374.2 K or 101.2 °C (d) The reaction is endothermic, so an increase in the value of K as calculated in parts (a)–(c) should be accompanied by an increase in T.
CHAPTER 20
20.1 In a Brønsted–Lowry acid-base reaction, H+ is transferred from the acid to the base. In a redox reaction, one or more electrons are transferred from the reductant to the oxidant. The greater the tendency of an acid to donate H+, the lesser the tendency of its conjugate base to accept H+. The stronger the acid, the weaker its conjugate base. Similarly, the greater the tendency of a reduced species to donate electrons, the lesser the tendency of the corresponding oxidized species to accept electrons. The stronger the reducing agent, the weaker the corresponding oxidizing agent.
20.4 (a) Add 1 M A2+ (aq) to the beaker with the A(s) electrode. Add 1 M B2+(aq) to the beaker with the B(s) electrode. Add a salt bridge to enable the flow of ions from one compartment to the other. (b) The A electrode functions as the cathode. (c) Electrons flow through the external circuit from the anode to the cathode, from B to A in this cell. ![]() .
.
20.7 (a) The sign of ΔG° is positive. (b) The equilibrium constant is less than one. (c) No. An electrochemical cell based on this reaction cannot accomplish work on its surroundings.
20.9 (a) Line 1 ![]() .
.
20.13 (a) Oxidation is the loss of electrons. (b) Electrons appear on the products' side (right side). (c) The oxidant is the reactant that is reduced. (d) An oxidizing agent is the substance that promotes oxidation; it is the oxidant.
20.15 (a) True (b) false (c) true
20.17 (a) I, +5 to 0; C, +2 to +4 (b) Hg, +2 to 0; N, – 2 to 0 (c) N, +5 to +2; S, – 2 to 0 (d) Cl, +4 to +3; O, –1 to 0
20.19 (a) TiCl4(g) + 2 Mg(l) ![]() Ti(s) + 2 MgCl2(l) (b) Mg(l) is oxidized; TiCl4(g) is reduced. (c) Mg(l) is the reductant; TiCl4(g) is the oxidant.
Ti(s) + 2 MgCl2(l) (b) Mg(l) is oxidized; TiCl4(g) is reduced. (c) Mg(l) is the reductant; TiCl4(g) is the oxidant.
20.21 (a) Sn2+(aq) ![]() Sn4+ (aq) + 2e–, oxidation (b) TiO2 (s) + 4 H+ (aq) + 2e
Sn4+ (aq) + 2e–, oxidation (b) TiO2 (s) + 4 H+ (aq) + 2e ![]() Ti2+(aq) + 2 H2O(l), reduction (c) ClO3–(aq) + 6 H+ (aq) + 6e–
Ti2+(aq) + 2 H2O(l), reduction (c) ClO3–(aq) + 6 H+ (aq) + 6e–![]() Cl– (aq) + 3 H2O(l), reduction (d) N2(g) + 8 H+ (aq) + 6e–
Cl– (aq) + 3 H2O(l), reduction (d) N2(g) + 8 H+ (aq) + 6e–![]() 2 NH4+ (aq), reduction (e) 4 OH– (aq)
2 NH4+ (aq), reduction (e) 4 OH– (aq) ![]() O2(g) + 2 H2O(l) + 4e–, oxidation (f) SO32–(aq) + 2 OH–(aq)
O2(g) + 2 H2O(l) + 4e–, oxidation (f) SO32–(aq) + 2 OH–(aq) ![]() SO42–(aq) + H2O(l) + 2e–, oxidation (g) N2(g) + 6 H2O(l) + 6e– 2 NH3(g) + 6 OH–(aq), reducation
SO42–(aq) + H2O(l) + 2e–, oxidation (g) N2(g) + 6 H2O(l) + 6e– 2 NH3(g) + 6 OH–(aq), reducation
20.23 (a) Cr2O72–(aq) + I–(aq) + 8 H+(aq) ![]() 2 Cr3+(aq) + IO3–(aq) + 4 H2O(l); oxidizing agent, Cr2O72– reducing agent, I– (b) 4MnO4–(aq) + 5 CH3OH(aq) + 12 H+ (aq) 4Mn2+ (aq) + 5 HCO2H(aq) + 12 H2O(aq); oxidizing agent, MnO4–; reducing agent, CH3OH (c) I2(s) + 5 OCl–(aq) + H2O(l)
2 Cr3+(aq) + IO3–(aq) + 4 H2O(l); oxidizing agent, Cr2O72– reducing agent, I– (b) 4MnO4–(aq) + 5 CH3OH(aq) + 12 H+ (aq) 4Mn2+ (aq) + 5 HCO2H(aq) + 12 H2O(aq); oxidizing agent, MnO4–; reducing agent, CH3OH (c) I2(s) + 5 OCl–(aq) + H2O(l) ![]() 2 IO3–(aq) + 5 Cl–(aq) + 2 H+(aq); oxidizing agent, OCl–; reducing agent, l2 (d) As2O3(s) + 2 NO3–(aq) + 2 H2O(l) + 2 H+ (aq)
2 IO3–(aq) + 5 Cl–(aq) + 2 H+(aq); oxidizing agent, OCl–; reducing agent, l2 (d) As2O3(s) + 2 NO3–(aq) + 2 H2O(l) + 2 H+ (aq) ![]() 2 H3AsO4(aq) + N2O3(aq); oxidizing agent, NO3–; reducing agent, As2O3 (e) 2 MnO4–(aq) + Br–(aq) + H2O(l)
2 H3AsO4(aq) + N2O3(aq); oxidizing agent, NO3–; reducing agent, As2O3 (e) 2 MnO4–(aq) + Br–(aq) + H2O(l) ![]() 2 MnO2(s) + BrO3–(aq) + 2 OH–(aq); oxidizing agent, MnO4–; reducing agent, Br– (f) Pb(OH)42–(aq) + ClO–(aq)
2 MnO2(s) + BrO3–(aq) + 2 OH–(aq); oxidizing agent, MnO4–; reducing agent, Br– (f) Pb(OH)42–(aq) + ClO–(aq) ![]() PbO2(s) + Cl–(aq) + 2 OH–(aq) + H2O(l); oxidizing agent, ClO–; reducing agent, Pb(OH)42–
PbO2(s) + Cl–(aq) + 2 OH–(aq) + H2O(l); oxidizing agent, ClO–; reducing agent, Pb(OH)42–
20.25 (a) The reaction Cu2+(aq) + Zn(s) ![]() Cu(s) + Zn2+(aq) is occurring in both figures. In Figure 20.3 the reactants are in contact, while in Figure 20.4 the oxidation half–reaction and reduction halfreaction are occurring in separate compartments. In Figure 20.3 the flow of electrons cannot be isolated or utilized; in Figure 20.4 electrical current is isolated and flows through the voltmeter. (b) Na+ cations are drawn into the cathode compartment to maintain charge balance as Cu2+ ions are removed.
Cu(s) + Zn2+(aq) is occurring in both figures. In Figure 20.3 the reactants are in contact, while in Figure 20.4 the oxidation half–reaction and reduction halfreaction are occurring in separate compartments. In Figure 20.3 the flow of electrons cannot be isolated or utilized; in Figure 20.4 electrical current is isolated and flows through the voltmeter. (b) Na+ cations are drawn into the cathode compartment to maintain charge balance as Cu2+ ions are removed.
20.27 (a) Fe(s) is oxidized, Ag+(aq) is reduced (b) Ag+ (aq) + e–![]() Ag(s); Fe(s)
Ag(s); Fe(s) ![]() Fe2+(aq) + 2e– (c) Fe(s) is the anode, Ag(s) is the cathode. (d) Fe(s) is negative; Ag(s) is positive. (e) Electrons flow from the Fe electrode (–) toward the Ag electrode (+). (f) Cations migrate toward the Ag(s) cathode; anions migrate toward the Fe(s) anode.
Fe2+(aq) + 2e– (c) Fe(s) is the anode, Ag(s) is the cathode. (d) Fe(s) is negative; Ag(s) is positive. (e) Electrons flow from the Fe electrode (–) toward the Ag electrode (+). (f) Cations migrate toward the Ag(s) cathode; anions migrate toward the Fe(s) anode.
20.29 Electromotive force, emf, is the potential energy difference between an electron at the anode and an electron at the cathode of a voltaic cell. (b) One volt is the potential energy difference required to impart 1 J of energy to a charge of 1 coulomb. (c) Cell potential, Ecell, is the emf of an electrochemical cell.
20.31 (a) 2 H+(aq) + 2e–![]() H2(g) (b) A standard hydrogen electrode, SHE, has components that are at standard conditions, 1 M H+ (aq) and H2(g) at 1 atm. (c) The platinum foil in a SHE serves as an inert electron carrier and a solid reaction surface.
H2(g) (b) A standard hydrogen electrode, SHE, has components that are at standard conditions, 1 M H+ (aq) and H2(g) at 1 atm. (c) The platinum foil in a SHE serves as an inert electron carrier and a solid reaction surface.
20.33 (a) A standard reduction potential is the relative potential of a reduction halfreaction measured at standard conditions. (b) E°red = 0V
20.35 (a) Cr2+(aq) ![]() Cr3+(aq) + e–; Tl3+(aq) + 2e–
Cr3+(aq) + e–; Tl3+(aq) + 2e–![]() Tl+(aq) (b) E°red = 0.78 V
Tl+(aq) (b) E°red = 0.78 V
(c)
20.37 (a) E° = 0.823 V (b) E° = 1.89 V (c) E° = 1.211 V (d) E° = 0.62 V
20.39 (a) 3 Ag+(aq)+Cr(s) ![]() 3 Ag(s) + Cr3+(aq), E° = 1.54 V (b) Two of the combinations have essentially equal E° values: 2 Ag+(aq) + Cu(s)
3 Ag(s) + Cr3+(aq), E° = 1.54 V (b) Two of the combinations have essentially equal E° values: 2 Ag+(aq) + Cu(s) ![]() 2 Ag(s) + Cu2+(aq), E° = 0.462 V; 3 Ni2+(aq) + 2 Cr(s)
2 Ag(s) + Cu2+(aq), E° = 0.462 V; 3 Ni2+(aq) + 2 Cr(s) ![]() 3 Ni(s) + 2 Cr3+(aq), E° = 0.46 V
3 Ni(s) + 2 Cr3+(aq), E° = 0.46 V
20.41 (a) Anode, Sn(s); cathode, Cu(s). (b) The copper electrode gains mass as Cu is plated out, and the tin electrode loses mass as Sn is oxidized. (c) Cu2+(aq) + Sn(s) ![]() Cu(s) + Sn2+(aq). (d) E° = 0.473 V.
Cu(s) + Sn2+(aq). (d) E° = 0.473 V.
20.43 (a) Mg(s) (b) Ca(s) (c) H2(g) (d) BrO3–(aq)
20.45 (a) Cl2(aq), strong oxidant (b) MnO4–(aq), acidic, strong oxidant (c) Ba(s) strong reductant (d) Zn(s), reductant
20.47 (a) Cu2+ (aq) < O2(g) < Cr2O72– (aq) < Cl2(g) < H2O2(aq) (b) H2O2(aq) < I–(aq) < Sn2+(aq) < Zn(s) < Al(s)
20.49 Al and H2C2O4
20.51 (a) 2 Fe2+(aq) + S2O62–(aq) + 4 H+(aq) ![]() 2 Fe3+(aq) + 2 H2SO3(aq); 2 Fe2+ (aq) + N2O(aq) + 2 H+ (aq)
2 Fe3+(aq) + 2 H2SO3(aq); 2 Fe2+ (aq) + N2O(aq) + 2 H+ (aq) ![]() 2 Fe3+(aq) + N2(g) + H2O(l); Fe2+(aq) + VO2+(aq) + 2 H+(aq)
2 Fe3+(aq) + N2(g) + H2O(l); Fe2+(aq) + VO2+(aq) + 2 H+(aq) ![]() Fe3+(aq) + VO2+(aq) + H2O(l) (b) E° = –0.17 V, ΔG° = 33kJ; E° = –2.54 V, ΔG° = 4.90 × 102 kJ; E° = 0.23 V, ΔG° = –22kJ (c) K = 1.8 × 10–6 = 10–6; K = 1.2 × 10–86 = 10–86; K = 7.8 × 103 = 8 × 103
Fe3+(aq) + VO2+(aq) + H2O(l) (b) E° = –0.17 V, ΔG° = 33kJ; E° = –2.54 V, ΔG° = 4.90 × 102 kJ; E° = 0.23 V, ΔG° = –22kJ (c) K = 1.8 × 10–6 = 10–6; K = 1.2 × 10–86 = 10–86; K = 7.8 × 103 = 8 × 103
20.53 ΔG° = 21.8kJ, ![]() = –0.113 V
= –0.113 V
20.55 (a) E° = 0.16V, K = 2.54 × 105 = 3 × 105 (b) E° = 0.277 V, K = 2.3 × 109 (c) E° = 0.45 V, K = 1.5 × 1075 = 1075
20.57 (a) K = 9.8 × 102 (b) K = 9.5 × 105 (c) K = 9.3 × 108
20.59 (a) wmax = –130 kJ/mol Sn
20.61 (a) The Nernst equation is applicable when the components of an electrochemical cell are at nonstandard conditions. (b) Q = 1 (c) Q decreases and E increases
20.63 (a) E decreases (b) E decreases (c) E decreases (d) no effect
20.65 (a) E° = 0.48 V (b) E = 0.53 V (c) E = 0.46 V
20.67 (a) E° = 0.46 V (b) E = 0.37 V
20.69 (a) The compartment with [Zn2+] = 1.00 × 10–2M is the anode. (b) E° = 0 (c) E = 0.0668 V (d) In the anode compartment [Zn2+] increases; in the cathode compartment [Zn2+] decreases
20.71 E° = 0.763V, pH = 1.6
20.73 (a) The emf of a battery decreases as it is used The concentrations of products increase and the concentrations of reactants decrease, causing Q to increase and Ecell to decrease. (b) A D-size battery contains more reactants than a AA, enabling the D to provide power for a longer time.
20.75 (a) 464 g PbO2 (b) 3.74 × 105 C of charge transferred
20.77 (a) The anode (b) E° = 0.50 V (c) The emf of the battery, 3.5 V, is exactly the standard cell potential calculated in part (b). (d) At ambient conditions, E ≈ E°, so log Q ≈ 1. Assuming that the value of E° is relatively constant with temperature, the value of the second term in the Nernst equation is approximately zero at 37 °C, and E ≈ 3.5 V.
20.79 (a) The cell emf will have a smaller value. (b) NiMH batteries use an alloy such as ZrNi2 as the anode material. This eliminates the use and disposal problems associated with Cd, a toxic heavy metal.
20.81 The main advantage of a fuel cell is that fuel is continuously supplied, so that it can produce electrical current for a time limited only by the amount of available fuel. For the hydrogen-oxygen fuel cell, this is also a disadvantage because volatile and explosive hydrogen must be acquired and stored. Alkaline batteries are convenient, but they have a short lifetime, and the disposal of their zinc and manganese solids is more problematic than disposal of water produced by the hydrogenoxygen fuel cell.
20.83 (a) anode: Fe(s) ![]() Fe2+(aq) + 2e–; cathode: O2(g) + 4 H+(aq) + 4e–
Fe2+(aq) + 2e–; cathode: O2(g) + 4 H+(aq) + 4e–![]() 2 H2O(l) (b) 2 Fe2+(aq) + 3 H2O(l) + 3 H2O(l)
2 H2O(l) (b) 2 Fe2+(aq) + 3 H2O(l) + 3 H2O(l) ![]() Fe2O3 • 3 H2O(s) + 6 H+ (aq) + 2e– ; O2(g) + 4 H+(aq) + 4e–
Fe2O3 • 3 H2O(s) + 6 H+ (aq) + 2e– ; O2(g) + 4 H+(aq) + 4e–![]() 2 H2O(l)
2 H2O(l)
20.85 (a) Mg is called a “sacrificial anode” because it has a more negative ![]() than the pipe metal and is preferentially oxidized when the two are coupled. It is sacrificed to preserve the pipe. (b)
than the pipe metal and is preferentially oxidized when the two are coupled. It is sacrificed to preserve the pipe. (b) ![]() for Mg2+ is –2.37 V, more negative than most metals present in pipes, including Fe and Zn.
for Mg2+ is –2.37 V, more negative than most metals present in pipes, including Fe and Zn.
20.87 Under acidic conditions, air (O2) oxidation of Zn(s), 1.99 V; Fe(s), 1.67 V; and Cu(s), 0.893 V are all spontaneous. When the three metals are in contact, Zn will act as a sacrificial anode for both Fe and Cu, but after the Zn is depleted, Fe will be oxidized (corroded).
20.89 (a) Electrolysis is an electrochemical process driven by an outside energy source. (b) By definition, electrolysis reactions are nonspontaneous. (c) 2 Cl–(l) ![]() Cl2(g) + 2e– (d) When an aqueous solution of NaCl undergoes electrolysis, sodium metal is not formed because H2O is preferentially reduced to form H2(g).
Cl2(g) + 2e– (d) When an aqueous solution of NaCl undergoes electrolysis, sodium metal is not formed because H2O is preferentially reduced to form H2(g).
20.91 (a) 236 g Cr(s) (b) 2.51 A
20.93 (a) 4.0 × 105 g Li (b) The minimum voltage required to drive the electrolysis is + 4.41V.
20.95 Gold is less active than copper and thus more difficult to oxidize. When crude copper is refined by electrolysis, Cu is oxidized from the crude anode, but any metallic gold present in the crude copper is not oxidized, so it accumulates near the anode, available for collection.
20.97(a) 2 Ni+(aq) ![]() Ni(s) + Ni2+(aq) (b) 3 MnO42–(aq) + 4 H+ (aq)
Ni(s) + Ni2+(aq) (b) 3 MnO42–(aq) + 4 H+ (aq) ![]() 2 MnO4 (aq) + MnO2(s) + 2 H2O(l) (c) 3 H2SO3(aq)
2 MnO4 (aq) + MnO2(s) + 2 H2O(l) (c) 3 H2SO3(aq) ![]() S(s) + 2 HSO4–(aq) + 2 H+(aq) + H2O(l) (d) Cl2(aq) + 2 OH–(aq)
S(s) + 2 HSO4–(aq) + 2 H+(aq) + H2O(l) (d) Cl2(aq) + 2 OH–(aq) ![]() Cl–(aq) + ClO–(aq) + H2O(l)
Cl–(aq) + ClO–(aq) + H2O(l)
20.100 (a) E° = 0.627 V, spontaneous (b) E° = –0.82 V, nonspontaneous (c) E° = 0.93 V, spontaneous (d) E° = 0.183 V, spontaneous
20.104 K = 1.6 × 106
20.107 The ship's hull should be made negative. The ship, as a negatively charged “electrode,” becomes the site of reduction, rather than oxidation, in an electrolytic process.
20.110 3.0 × 104 kWh required
20.112 (a) H2 is being oxidized and N2 is being reduced. (b) K = 6.9 × 105 (c) E° = 0.05755 V
20.115 (a) E° = 0.028 V (b) cathode: Ag+(aq) + e–![]() Ag(s); anode: Fe2+(aq)
Ag(s); anode: Fe2+(aq) ![]() Fe3+(aq) + e– (c) ΔS° = 148.5 J. Since ΔS° is positive, ΔG° will become more negative and E° will become more positive as temperature is increased.
Fe3+(aq) + e– (c) ΔS° = 148.5 J. Since ΔS° is positive, ΔG° will become more negative and E° will become more positive as temperature is increased.
20.118 Ksp for AgSCN is 1.0 × 10–12
CHAPTER 21
21.1 (a) 24Ne; outside; reduce neutron-to-proton ratio via β decay (b) 32Cl; outside; increase neutron-to-proton ratio via positron emission or orbital electron capture (c) 108Sn; outside; increase neutron-to-proton ratio via positron emission or orbital electron capture (d) 216Po; outside; nuclei with Z ≥ 84 usually decay via α emission.
21.4 (a) 7 min (b) 0.1 min–1 (c) 30% (3/10) of the sample remains after 12 min. (d) ![]()
21.5 (a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
21.7 (a) 25 protons, 30 neutrons (b) 80 protons, 121 neutrons (c) 19 protons, 20 neutrons
21.9 (a) ![]()
21.11 (a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
21.13 (a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
21.15 7 alpha emissions, 4 beta emissions
21.17 (a) Positron emission (for low atomic numbers, positron emission is more common than electron capture) (b) beta emission (c) beta emission (d) beta emission
21.19 (a) Stable: ![]() 20 neutrons is a magic number (b) stable:
20 neutrons is a magic number (b) stable: ![]() 126 neutrons is a magic number (c) stable:
126 neutrons is a magic number (c) stable: ![]() even proton, even neutron more likely to be stable;
even proton, even neutron more likely to be stable; ![]() has high neutron-to-proton ratio
has high neutron-to-proton ratio
21.21 ![]()
21.23 The alpha particle, ![]() has a magic number of both protons and neutrons, while the proton is an odd proton, even neutron particle. Alpha is a very stable emitted particle, which makes alpha emission a favorable process. The proton is not a stable emitted particle, and its formation does not encourage proton emission as a process.
has a magic number of both protons and neutrons, while the proton is an odd proton, even neutron particle. Alpha is a very stable emitted particle, which makes alpha emission a favorable process. The proton is not a stable emitted particle, and its formation does not encourage proton emission as a process.
21.25 Protons and alpha particles are positively charged and must be moving very fast to overcome electrostatic forces that would repel them from the target nucleus. Neutrons are electrically neutral and not repelled by the nucleus.
21.27 (a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
21.29 (a) ![]() (b)
(b) ![]() (c)
(c) ![]()
21.31 (a) True. The decay rate constant and half-life are inversely related. (b) False. If X is not radioactive, its half-life is essentially infinity. (c) True. Changes in the amount of A would be substantial and measurable over the 40-year time frame, while changes in the amount of X would be very small and difficult to detect.
21.33 When the watch is 50 years old, only 6% of the tritium remains. The dial will be dimmed by 94%.
21.35 The source must be replaced after 2.18 yr or 26.2 months; this corresponds to August 2012.
21.37 (a) 1.1 × 1011 alpha particles emitted in 5.0 min (b) 9.9 mCi
21.39 k = 1.21 × 10–4 yr–1; t = 4.3 × 103 yr
21.41 k = 5.46 × 10–10 yr–1; t = 3.0 × 109 yr
21.43 The energy released when one mole of Fe2O3 reacts is 8.515 × 103 J. The energy released when one mole of ![]() is formed from protons and neutrons is 2.73 × 1012J. This is 3 × 108 or 300 million times as much energy as the thermite reaction.
is formed from protons and neutrons is 2.73 × 1012J. This is 3 × 108 or 300 million times as much energy as the thermite reaction.
21.45 Δm = 0.2414960 amu, ΔE = 3.604129 × 10–11 J/27 Al nucleus required, 8.044234 × 1013 J/100 27 g Al
21.47 (a) Nuclear mass: 2H, 2.013553 amu; 4He, 4.001505 amu; 6Li, 6.0134771 amu (b) nuclear binding energy: 2H, 3.564 × 10–13J; 4He, 4.5336 × 10–12J; 6Li, 5.12602 10–12 J (c) binding energy/nucleon; 2H, 1.782 × 10–13 J/nucleon; 4He, 1.1334 × 10–12 J/nucleon; 6Li, 8.54337 × 10–13J/nucleon. This trend in binding energy/nucleon agrees with the curve in Figure 21.12. The anomalously high calculated value for 4He is also apparent on the figure.
21.49 (a) 1.71 × 105 kg/d (b) 2.1 × 108 g 235U
21.51 (a) 59Co; it has the largest binding energy per nucleon, and binding energy gives rise to mass defect.
21.53 (a) Nal is a good source of iodine because iodine is a large percentage of its mass; it is completely dissociated into ions in aqueous solution, and iodine in the form of I–(aq) is mobile and immediately available for biouptake. (b) A Geiger counter placed near the thyroid immediately after ingestion will register background, then gradually increase in signal until the concentration of iodine in the thyroid reaches a maximum. Over time, iodine-131 decays, and the signal decreases. (c) The radioactive iodine will decay to 0.01% of the original amount in approximately 82 days.
21.55 235U
21.57 The control rods in a nuclear reactor regulate the flux of neutrons to keep the reaction chain self-sustaining and also prevent the reactor core from overheating. They are composed of materials such as boron or cadmium that absorb neutrons.
21.59 (a) ![]() (b)
(b) ![]()
21.61 (a) Δm = 0.006627 g/mol; ΔE = 5.956 × 1011J = 5.956 × 108kJ/mol ![]() (b) The extremely high temperature is required to overcome electrostatic charge repulsions between the nuclei so that they can come together to react.
(b) The extremely high temperature is required to overcome electrostatic charge repulsions between the nuclei so that they can come together to react.
21.63 (a) Boiling water reactor (b) fast breeder reactor (c) gas-cooled reactor
21.65 Hydrogen abstraction: RCOOH + •OH ![]() RCOO• + H2O; deprotonation: RCOOH + OH–
RCOO• + H2O; deprotonation: RCOOH + OH–![]() RCOO– + H2O. Hydroxyl radical is more toxic to living systems because it produces other radicals when it reacts with molecules in the organism. Hydroxide ion, OH–, on the other hand, will be readily neutralized in the buffered cell environment. The acid-base reactions of OH– are usually much less disruptive to the organism than the chain of redox reactions initiated by •OH radical.
RCOO– + H2O. Hydroxyl radical is more toxic to living systems because it produces other radicals when it reacts with molecules in the organism. Hydroxide ion, OH–, on the other hand, will be readily neutralized in the buffered cell environment. The acid-base reactions of OH– are usually much less disruptive to the organism than the chain of redox reactions initiated by •OH radical.
21.67 (a) 5.3 × 108 dis/s, 5.3 × 108 Bq (b) 6.1 × 102 mrad, 6.1 × 10–3 Gy (c) 5.8 × 103 mrem, 5.8 × 10–2 Sv
21.69 ![]()
21.70 (a) ![]() (b) 35Cl and 37Cl both have an odd number of protons but an even number of neutrons. 36Cl has an odd number of protons and neutrons, so it is less stable than the other two isotopes.
(b) 35Cl and 37Cl both have an odd number of protons but an even number of neutrons. 36Cl has an odd number of protons and neutrons, so it is less stable than the other two isotopes.
21.73 (a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
21.77 The C — OH bond of the acid and the O — H bond of the alcohol break in this reaction. Initially, 18O is present in the C — 18OH group of the alcohol. In order for 18O to end up in the ester, the 18O — H bond of the alcohol must break. This requires that the C — OH bond in the acid also breaks. The unlabeled O from the acid ends up in the H2O product.
21.79 7Be, 8.612 × 10–13 J/nucleon; 9Be, 1.035 × 10–12 J/nucleon; 10Be: 1.042 × 10–12 J/nucleon. The binding energies/nucleon for 9Be and 10Be are very similar; that for 10Be is slightly higher.
21.85 1.4 × 104 kg C8H18
CHAPTER 22
22.1 (a) C2H4, the structure on the left, is the stable compound. Carbon can form strong multiple bonds to satisfy the octet rule, while silicon cannot. (b) The geometry about the central atoms in C2H4 is trigonal planar.
22.3 Molecules (b) and (d) will have the seesaw structure shown in the figure.
22.6 (c) Density, the ratio of mass to volume, increases going down the family; only this trend is consistent with the data in the figure. Other properties do not match the trend because (a) electronegativity and (b) first ionization energy both decrease rather than increase going down the family. Trends for both (d) X — X single bond enthalpy and (e) electron affinity are somewhat erratic, with the trends decreasing from S to Po, and anomalous values for the properties of O, probably owing to its small covalent radius.
22.9 The compound on the left, with the strained three-membered ring, will be the most generally reactive. The larger the deviation from ideal bond angles, the more strain in the molecule and the more generally reactive it is.
22.11 Metals: (b) Sr, (c) Mn, (e) Na; nonmetals: (a) P, (d) Se, (f) Kr; metalloids: none.
22.13 (a) O (b) Br (c) Ba (d) O (e) Co (f) Br
22.15 (a) N is too small a central atom to fit five fluorine atoms, and it does not have available d orbitals, which can help accommodate more than eight electrons. (b) Si does not readily form p bonds, which are necessary to satisfy the octet rule for both atoms in the molecule. (c) As has a lower electronegativity than N; that is, it more readily gives up electrons to an acceptor and is more easily oxidized.
22.17 (a) NaOCH3(s) + H2O(l) ![]() NaOH(aq) + CH3OH(aq) (b) CuO(s) + 2HNO3(aq)
NaOH(aq) + CH3OH(aq) (b) CuO(s) + 2HNO3(aq) ![]() Cu(NO3)2(aq) + H2O(l) (c) WO3(s) + 3H2(g)
Cu(NO3)2(aq) + H2O(l) (c) WO3(s) + 3H2(g) ![]() W(s) + 3H2O(g) (d) 4NH2OH(l) + O2(g)
W(s) + 3H2O(g) (d) 4NH2OH(l) + O2(g) ![]() 6H2O(l) + 2N2(g) (e) Al4C3(s) + 12H2O(l)
6H2O(l) + 2N2(g) (e) Al4C3(s) + 12H2O(l) ![]() 4Al(OH)3(s) + 3CH4(g)
4Al(OH)3(s) + 3CH4(g)
22.19(a) ![]() protium;
protium; ![]() , deuterium;
, deuterium; ![]() tritium (b) in order of decreasing natural abundance: protium > deuterium > tritium (c) Tritium is radioactive. (d)
tritium (b) in order of decreasing natural abundance: protium > deuterium > tritium (c) Tritium is radioactive. (d) ![]()
22.21 Like other elements in group 1A, hydrogen has only one valence electron and its most common oxidation number is +1.
22.23 (a) Mg(s) + 2 H+(aq) ![]() Mg2+(aq) + H2(g) (b) C(s) + H2O(g)
Mg2+(aq) + H2(g) (b) C(s) + H2O(g) ![]() CO(g) + 3H2(g) (c) CH4(g) + H2O(g)
CO(g) + 3H2(g) (c) CH4(g) + H2O(g) ![]() CO(g) + 3H2(g)
CO(g) + 3H2(g)
22.25 (a) NaH(s) + H2O(l) ![]() NaOH(aq) + H2(g) (b) Fe(s) + H2SO4(aq)
NaOH(aq) + H2(g) (b) Fe(s) + H2SO4(aq) ![]() Fe2+ (aq) + H2(g) + SO42– (aq) (c) H2(g) + Br2(g)
Fe2+ (aq) + H2(g) + SO42– (aq) (c) H2(g) + Br2(g) ![]() 2 HBr(g) (d) 2 Na(l) + H2(g)
2 HBr(g) (d) 2 Na(l) + H2(g) ![]() 2 NaH(s) (e) PbO(s) + H2(g)
2 NaH(s) (e) PbO(s) + H2(g) ![]() Pb(s) + H2O(g)
Pb(s) + H2O(g)
22.27 (a) Ionic (b) molecular (c) metallic
22.29 Vehicle fuels produce energy via combustion reactions. The combustion of hydrogen is very exothermic and its only product, H2O, is a nonpollutant.
22.31 Xenon has a lower ionization energy than argon; because the valence electrons are not as strongly attracted to the nucleus, they are more readily promoted to a state in which the atom can form bonds with fluorine. Also, Xe is larger and can more easily accommodate an expanded octet of electrons.
22.33 (a) Ca(OBr)2, Br, +1 (b) HBrO3, Br, +5 (c) XeO3, Xe, +6 (d) ClO4– Cl, +7 (e) HIO2, I, +3 (f) IF5; I, +5; F, –1
22.35 (a) iron(III) chlorate, Cl, +5 (b) chlorous acid, Cl, +3 (c) xenon hexafluoride, F, –1 (d) bromine pentafluoride; Br, + 5; F, –1 (e) xenon oxide tetrafluoride, F, –1 (f) iodic acid, I, +5
22.37 (a) van der Waals intermolecular attractive forces increase with increasing number of electrons in the atoms. (b) F2 reacts with water: F2(g) + H2O(l) ![]() 2 HF(g) + O2(g). That is, fluorine is too strong an oxidizing agent to exist in water. (c) HF has extensive hydrogen bonding. (d) Oxidizing power is related to electronegativity. Electronegativity and oxidizing power decrease in the order given.
2 HF(g) + O2(g). That is, fluorine is too strong an oxidizing agent to exist in water. (c) HF has extensive hydrogen bonding. (d) Oxidizing power is related to electronegativity. Electronegativity and oxidizing power decrease in the order given.
22.39(a) 2 HgO(s) ![]() 2 Hg(l) + O2(g) (b) 2 Cu(NO3)2(s)
2 Hg(l) + O2(g) (b) 2 Cu(NO3)2(s) ![]() 2 CuO(s) + 4NO2(g) + O2(g) (c) PbS(s) + 4 O3(g)
2 CuO(s) + 4NO2(g) + O2(g) (c) PbS(s) + 4 O3(g) ![]() PbSO4(s) + 4 O2(g) (d) 2 ZnS(s) + 3 O2(g)
PbSO4(s) + 4 O2(g) (d) 2 ZnS(s) + 3 O2(g) ![]() 2 ZnO(s) + 2 SO2(g) (e) 2 K2O2(s) + 2 CO2(g)
2 ZnO(s) + 2 SO2(g) (e) 2 K2O2(s) + 2 CO2(g) ![]() 2 K2CO3(s) + O2(g) (f) 3O2(g)
2 K2CO3(s) + O2(g) (f) 3O2(g) ![]() 2O3(g)
2O3(g)
22.41 (a) acidic (b) acidic (c) amphoteric (d) basic
22.43 (a) H2SeO3, Se, +4 (b) KHSO3, S, +4 (c) H2Te, Te, –2 (d) CS2, S, –2 (e) CaSO4, S, +6 (f) CdS, S, –2 (g) ZnTe, Te, –2
22.45 (a) 2 Fe3+(aq) + H2S(aq) ![]() 2 Fe2+(aq) + S(s) + 2 H+(aq) (b) Br2(l) + H2S(aq)
2 Fe2+(aq) + S(s) + 2 H+(aq) (b) Br2(l) + H2S(aq) ![]() 2 Br–(aq) + S(s) + 2 H+(aq) (c) 2 MnO4–(aq) + 6 H+ (aq) + 5 H2S(aq)
2 Br–(aq) + S(s) + 2 H+(aq) (c) 2 MnO4–(aq) + 6 H+ (aq) + 5 H2S(aq) ![]() 2 Mn2+ (aq) + 5 S(s) + 8 H2O(l) (d) 2 NO3–(aq) + H2S(aq) + 2 H+(aq)
2 Mn2+ (aq) + 5 S(s) + 8 H2O(l) (d) 2 NO3–(aq) + H2S(aq) + 2 H+(aq) ![]() 2 NO2(aq) + S(s) + 2 H2O(l)
2 NO2(aq) + S(s) + 2 H2O(l)
22.47
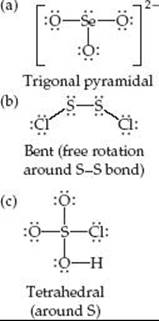
22.49 (a) SO2(s) + H2O(l) ![]() H2SO3(aq)
H2SO3(aq) ![]() H+ (aq) + HSO3– (aq) (b) ZnS(s) + 2 HCl(aq)
H+ (aq) + HSO3– (aq) (b) ZnS(s) + 2 HCl(aq) ![]() ZnCl2(aq) + H2S(g) (c) 8 SO32–(aq) + S8(s)
ZnCl2(aq) + H2S(g) (c) 8 SO32–(aq) + S8(s) ![]() 8 S2O32–(aq) (d) SO3(aq) + H2SO4(l)
8 S2O32–(aq) (d) SO3(aq) + H2SO4(l) ![]() H2S2O7(l)
H2S2O7(l)
22.51 (a) NaNO2, +3 (b) NH3, –3 (c) N2O,+1 (d) NaCN, –3 (e) HNO3, + 5 (f) NO2, +4 (g) N2, 0 (h) BN, –3
22.53 (a) ![]()
The molecule is bent around the central oxygen and nitrogen atoms; the four atoms need not be coplanar. The right-most form does not minimize formal charges and is less important in the actual bonding model. The oxidation state of N is +3.
(b)
![]()
The molecule is linear. The oxidation state of N is –1/3.
(c)
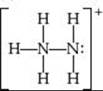
The geometry is tetrahedral around the left nitrogen, trigonal pyramidal around the right. The oxidation state of N is – 2.
(d)
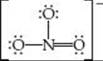
The ion is trigonal planar; it has three equivalent resonance forms. The oxidation state of N is +5.
22.55 (a) Mg3N2(s) + 6 H2O(l) ![]() 3 Mg(OH)2(s) + 2 NH3(aq) (b) 2 NO(g) + O2(g)
3 Mg(OH)2(s) + 2 NH3(aq) (b) 2 NO(g) + O2(g) ![]() 2 NO2(g), redox reaction (c) N2O5(g) + H2O(l)
2 NO2(g), redox reaction (c) N2O5(g) + H2O(l) ![]() 2 H+ (aq) + 2 NO3–(aq) (d) NH3(aq) + H+(aq)
2 H+ (aq) + 2 NO3–(aq) (d) NH3(aq) + H+(aq) ![]() NH4+(aq) (e) N2H4(l) + O2(g)
NH4+(aq) (e) N2H4(l) + O2(g) ![]() N2(g) + 2 H2O(g), redox reaction
N2(g) + 2 H2O(g), redox reaction
22.57 (a) HNO2(aq) + H2O(l) ![]() NO3–(aq) + 2e– (b) N2(g) + H2O(l)
NO3–(aq) + 2e– (b) N2(g) + H2O(l) ![]() N2O(aq) + 2 H+(aq) + 2e–
N2O(aq) + 2 H+(aq) + 2e–
22.59 (a) H3PO3, +3 (b) H4P2O7, +5 (c) SbCl3, +3 (d) Mg3As2, +5 (e) P2O5, +5 (f) Na3PO4, +5
22.61 (a) Phosphorus is a larger atom than nitrogen, and P has energetically available 3d orbitals, which participate in the bonding, but nitrogen does not. (b) Only one of the three hydrogens in H3PO2 is bonded to oxygen. The other two are bonded directly to phosphorus and are not easily ionized. (c) PH3 is a weaker base than H2O so any attempt to add H+ to PH3 in the presence of H2O causes protonation of H2O. (d) The P4 molecules in white phosphorus have more severely strained bond angles than the chains in red phosphorus, causing white phosphorus to be more reactive.
22.63 (a) 2 Ca3PO4(s) + 6 SiO2(s) + 10 C(s) ![]() P4(g) + 6 CaSiO3(l) +10 CO(g) (b) PBr3(l) + 3 H2O(l)
P4(g) + 6 CaSiO3(l) +10 CO(g) (b) PBr3(l) + 3 H2O(l) ![]() H3PO3(aq) + 3 HBr(aq) (c) 4PBr3(g) + 6H2(g)
H3PO3(aq) + 3 HBr(aq) (c) 4PBr3(g) + 6H2(g) ![]() P4(g) + 12HBr(g)
P4(g) + 12HBr(g)
22.65 (a) HCN (b) Ni(CO)4 (c) Ba(HCO3)2 (d) CaC2 (e) K2CO3
22.67 (a) ZnCO3(s) ![]() ZnO(s) + CO2(g) (b) BaC2(s) + 2 H2O(l)
ZnO(s) + CO2(g) (b) BaC2(s) + 2 H2O(l) ![]() Ba2+ (aq) + 2 OH– (aq) + C2H2(g) (c) 2 C2H2(g) + 5 O2(g)
Ba2+ (aq) + 2 OH– (aq) + C2H2(g) (c) 2 C2H2(g) + 5 O2(g) ![]() 4 CO2(g) + 2 H2O(g) (d) CS2(g) + 3 O2(g)
4 CO2(g) + 2 H2O(g) (d) CS2(g) + 3 O2(g) ![]() CO2(g) + 2 SO2(g) (e) Ca(CN)2(s) + 2 HBr(aq)
CO2(g) + 2 SO2(g) (e) Ca(CN)2(s) + 2 HBr(aq) ![]() CaBr2(aq) + 2 HCN(aq)
CaBr2(aq) + 2 HCN(aq)
22.69 (a) 2 CH4(g) + 2NH3(g) + 3O2(g) ![]() 2 HCN(g) + 6 H2O(g) (b) NaHCO3(s) + H+ (aq)
2 HCN(g) + 6 H2O(g) (b) NaHCO3(s) + H+ (aq) ![]() CO2(g) + H2O(l) + Na+ (aq) (c) 2 BaCO3(s) + O2(g) + 2 SO2(g)
CO2(g) + H2O(l) + Na+ (aq) (c) 2 BaCO3(s) + O2(g) + 2 SO2(g) ![]() 2 BaSO4(s) + 2 CO2(g)
2 BaSO4(s) + 2 CO2(g)
22.71 (a) H3BO3, +3 (b) SiBr4, +4 (c) PbCl2, +2 (d) Na2B4O7 • 10 H2O, +3 (e) B2O3, +3 (f) GeO2, +4
22.73 (a) Tin (b) carbon, silicon, and germanium (c) silicon
22.75 (a) Tetrahedral (b) Metasilicic acid will probably adopt the single-strand silicate chain structure shown in Figure 22.34(b). The Si to O ratio is correct and there are two terminal O atoms per Si that can accommodate the two H atoms associated with each Si atom of the acid.
22.77 (a) Diborane has bridging H atoms linking the two B atoms. The structure of ethane has the C atoms bound directly, with no bridging atoms. (b) B2H6 is an electron-deficient molecule. The 6 valence electron pairs are all involved in B — H sigma bonding, so the only way to satisfy the octet rule at B is to have the bridging H atoms shown in Figure 22.36. (c) The term hydridic indicates that the H atoms in B2H6 have more than the usual amount of electron density for a covalently bound H atom.
22.81 (a) SO2(g) + H2O(l) ![]() H2SO3(aq)
H2SO3(aq)
(b) Cl2O7(g) + H2O(l) ![]() 2HClO4(aq)
2HClO4(aq)
(c) Na2O2(s) + 2H2O(l) ![]() H2O2(aq) + 2NaOH(aq)
H2O2(aq) + 2NaOH(aq)
(d) BaC2(s) + 2H2O(l) ![]() Ba2+ (aq) + 2OH– (aq) + C2H2(g)
Ba2+ (aq) + 2OH– (aq) + C2H2(g)
(e) 2RbO2(s) + 2H2O(l) ![]() 2Rb+ (aq) + 2OH– (aq) + O2(g) + H2O2(aq)
2Rb+ (aq) + 2OH– (aq) + O2(g) + H2O2(aq)
(f) Mg3N2(s) + 6H2O(l) ![]() 3Mg(OH)2(s) + 2NH3(g)
3Mg(OH)2(s) + 2NH3(g)
(g) NaH(s) + H2O(l) ![]() NaOH(aq) + H2(g)
NaOH(aq) + H2(g)
22.85 (a) PO43–, + 5; NO3–, +5, (b) The Lewis structure for NO43– would be:
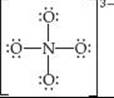
The formal charge on N is +1 and on each O atom is – 1. The four electronegative oxygen atoms withdraw electron density, leaving the nitrogen deficient. Since N can form a maximum of four bonds, it cannot form a π bond with one or more of the O atoms to regain electron density, as the P atom in PO43– does. Also, the short N — O distance would lead to a tight tetrahedron of O atoms subject to steric repulsion.
22.89 (a) 1.94 × 103 g H2 (b) 2.16 × 104 L H2 (c) 2.76 × 105 kJ
22.91 (a) –285.83 kJ/mol H2; –890.4 kJ/mol CH4 (b) –141.79 kJ/g H2; –55.50 kJ/g CH4 (c) 1.276 × 104kJ/m3 H2; 3.975 × 104kJ/m3CH4
22.95 (a) SO2(g) + 2 H2S(aq) ![]() 3 S(s) + 2 H2O(l) or 8 SO2(g) + 16 H2S(aq)
3 S(s) + 2 H2O(l) or 8 SO2(g) + 16 H2S(aq) ![]() 3 S8(s) + 16 H2O(l) (b) 4.0 × 103 mol = 9.7 × 104 LH2S (c) 1.9 × 105 g S produced
3 S8(s) + 16 H2O(l) (b) 4.0 × 103 mol = 9.7 × 104 LH2S (c) 1.9 × 105 g S produced
22.97 The average bond enthalpies are H — O, 463 kJ; H — S, 367 kJ; H — Se, 316 kJ; H — Te, 266 kJ. The H — X bond enthalpy decreases steadily in the series. The origin of this effect is probably the increasing size of the orbital from X with which the hydrogen 1s orbital must overlap.
22.101 Dimethylhydrazine produces 0.0369 mol gas per gram of reactants, while methylhydrazine produces 0.0388 mol gas per gram of reactants. Methylhydrazine has marginally greater thrust.
22.103(a) 3B2H6(g) + 6NH3(g) ![]() 2(BH)3(NH)3(l) + 12H2(g); 3LiBH4(s) + 3NH4Cl(s)
2(BH)3(NH)3(l) + 12H2(g); 3LiBH4(s) + 3NH4Cl(s) ![]() 2(BH)3(NH)3(l) + 9H2(g) + 3LiCl(s)
2(BH)3(NH)3(l) + 9H2(g) + 3LiCl(s)
(b)
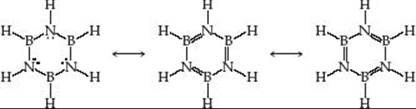
(c) 2.40 g (BH)3(NH)3
CHAPTER 23
23.2 (a)
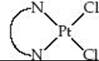
(b) Coordination number = 4, coordination geometry = square planar (c) oxidation state = +2
23.4 aminotrichloroplatinate(II)
23.6 Molecules (1), (3), and (4) are chiral because their mirror images are not superimposible on the original molecules.
23.8 (a) diagram (4) (b) diagram (1) (c) diagram (3) (d) diagram (2)
23.11 The lanthanide contraction is the name given to the decrease in atomic size due to the build-up in effective nuclear charge as we move through the lanthanides (elements 58-71) and beyond them. This effect offsets the expected increase in atomic size, decrease in ionization energy, and increase in electron affinity going from period 5 to period 6 transition elements. This causes the chemical properties of period 5 and period 6 elements in the same family to be even more similar than we would expect.
23.13 (a) All transition metal atoms have two s-electrons in their valence shell. Loss of these s-electrons leads to the +2 oxidation state common for most of the transition metals.
23.15 (a) Ti3+, [Ar]3d1 (b) Ru2+, [Kr]4d6 (c) Au3+, [Xe]4f145d8 (d) Mn4+, [Ar]3d3
23.17 (a) The unpaired electrons in a paramagnetic material cause it to be weakly attracted into a magnetic field. A diamagnetic material, where all electrons are paired, is very weakly repelled by a magnetic field.
23.19 The diagram shows a material with misaligned spins that become aligned in the direction of an applied magnetic field. This is a paramagnetic material.
23.21 (a) In Werner's theory, primary valence is the charge of the metal cation at the center of the complex. Secondary valence is the number of atoms bound or coordinated to the central metal ion. The modern terms for these concepts are oxidation state and coordination number, respectively. (b) Ligands are the Lewis base in metal-ligand interactions. As such, they must possess at least one unshared electron pair. NH3 has an unshared electron pair but BH3, with less than 8 electrons about B, has no unshared electron pair and cannot act as a ligand.
23.23 (a) +2 (b) 6 (c) 2 mol AgBr(s) will precipitate per mole of complex.
23.25 (a) Coordination number = 4, oxidation number = +2; 4 Cl– (b) 5, +4; 4 Cl–, 1 O2– (c) 6, +3; 4 N, 2 Cl– (d) 5, +2; 5 C (e) 6, +3; 6 O (f) 4, +2; 4 N
23.27 (a) A monodentate ligand binds to a metal via one atom, a bidentate ligand binds through two atoms. (b) Three bidentate ligands fill the coordination sphere of a six-coordinate complex. (c) A tridentate ligand has at least three atoms with unshared electron pairs in the correct orientation to simultaneously bind one or more metal ions.
23.29 (a) Ortho-phenanthroline, o-phen, is bidentate (b) oxalate, C2O42–, is bidentate (c) ethylenediaminetetraacetate, EDTA, is pentadentate (d) ethylenediamine, en, is bidentate.
23.31 (a) The term chelate effect refers to the special stability associated with formation of a metal complex containing a polydentate (chelate) ligand relative to a complex containing only monodentate ligands. (b) The increase in entropy, +ΔS, associated with the substitution of a chelating ligand for two or more monodentate ligands generally gives rise to the chelate effect. Chemical reactions with + ΔS tend to be spontaneous, have negative ΔG and large values of K. (c) Polydentate ligands are used as sequestering agents to bind metal ions and prevent them from undergoing unwanted chemical reactions without removing them from solution.
23.33 The ligand is not typically a chelate. The entire molecule is planar and the benzene rings on either side of the two N atoms inhibit their approach in the correct orientation for chelation.
23.35 (a) [Cr(NH3)6](NO3)3 (b) [Co(NH3)4CO3]2SO4 (c) [Pt(en)2Cl2]Br2 (d) K[V(H2O)2Br4] (e) [Zn(en)2][Hgl4]
23.37 (a) tetraamminedichlororhodium(III) chloride (b) potassium hexachlorotitanate(IV) (c) tetrachlorooxomolybdenum(VI) (d) tetraaqua(oxalato) platinum (IV) bromide
23.39
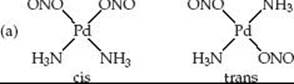
(b) [Pd(NH3)2(ONO)2], [Pd(NH3)2(NO2)2]
(c)
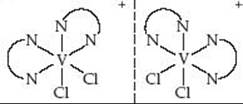
(d) [Co(NH3)4Br2]Cl, [Co(NH3)4BrCl]Br
23.41 Yes. No structural or stereoisomers are possible for a tetrahedral complex of the form MA2B2. The complex must be square planar with cis and trans geometric isomers.
23.43 (a) One isomer (b) trans and cis isomers with 180° and 90° Cl — Ir — Cl angles, respectively (c) trans and cis isomers with 180° and 90° Cl — Fe — Cl angles, respectively. The cis isomer is optically active.
23.45 (a) We cannot see the light with 300 nm wavelength, but we can see the 500 nm light. (b) Complementary colors are opposite each other on an artist's color wheel. (c) A colored metal complex absorbs visible light of its complementary color. (d) 196 kJ/mol
23.47 No. All 6 d-electrons in a low-spin octahedral Fe(II) complex will pair and occupy the low-energy dxy, dxz, and dyz orbitals. With no unpaired electrons, the complex cannot be paramagnetic.
23.49 Most of the attraction between a metal ion and a ligand is electrostatic. Whether the interaction is ion-ion or ion-dipole, the ligand is strongly attracted to the metal center and can be modeled as a point negative charge.
23.51 (a)
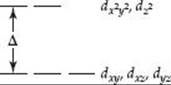
(b) The magnitude of Δ and the energy of the d-d transition for a d1 complex are equal. (c) Δ = 220 kJ/mol
23.53 A yellow color is due to absorption of light around 400 to 430 nm, a blue color to absorption near 620 nm. The shorter wavelength corresponds to a higher-energy electron transition and larger Δ value. Cyanide is a stronger-field ligand, and its complexes are expected to have larger Δ values than aqua complexes.
23.55 (a) Ti3+, d1 (b) Co3+, d6 (c) Ru3+, d5 (d) Mo5+, d1, (e) Re3+, d4
23.57 Yes. A weak-field ligand leads to a small Δ value and a small d-orbital splitting energy. If the splitting energy of a complex is smaller than the energy required to pair electrons in an orbital, the complex is high spin.
23.59 (a) Mn, [Ar]4s23d5; Mn2+, [Ar]3d5; 1 unpaired electron (b) Ru, [Kr]5s14d7; Ru2+, [Kr]4d6; 0 unpaired electrons (c) Rh, [Kr]5s14d8; Rh2+, [Kr]4d7; 1 unpaired electron
23.61 All complexes in this exercise are six-coordinate octahedral.
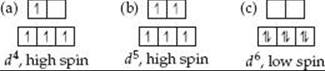
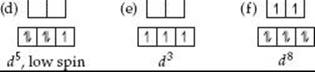
23.63
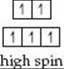
23.67 [Pt(NH3)6]Cl4; [Pt(NH3)4Cl2]Cl2; [Pt(NH3)3Cl3]Cl; [Pt(NH3)2Cl4]; K[Pt(NH3Cl5]
23.71 (a)
Both dmpe and en are bidentate ligands, binding through P and N, respectively. Because phosphorus is less electronegative than N, dmpe is a stronger electron pair donor and Lewis base than en. Dmpe creates a stronger ligand field and is higher on the spectrochemical series. Structurally, dmpe occupies a larger volume than en. M–P bonds are longer than M — N bonds and the two –CH3 groups on each P atom in dmpe create more steric hindrance than the H atoms on N in en. (b) The oxidation state of Mo is zero. (c) The symbol ![]() represents the bidentate dmpe ligand.
represents the bidentate dmpe ligand.
23.74 (a) Hemoglobin is the iron-containing protein that transports O2 in human blood. (b) Chlorophylls are magnesium-containing porphyrins in plants. They are the key components in the conversion of solar energy into chemical energy that can be used by living organisms. (c) Siderophores are iron-binding compounds or ligands produced by a microorganism. They compete on a molecular level for iron in the medium outside the organism and carry needed iron into the cells of the organism.
23.76 (a) Pentacarbonyliron(0) (b) The oxidation state of iron must be zero. (c) Two. One isomer has CN in an axial position and the other has it in an equatorial position.
23.78 (a)
(b) Visible light with λ = hc/Δ is absorbed by the complex, promoting one of the d electrons into a higher-energy d-orbital. The remaining wavelengths are reflected or transmitted; the combination of these wavelengths is the color we see. (c) [V(H2O)6]3+ will absorb light with higher energy because it has a larger Δ than [VF6]3–. H2O is in the middle of the spectrochemical series and causes a larger Δ than F–, a weak-field ligand.
23.80 [Co(NH3)6]3+, yellow; [Co(H2O)6]2+, pink; [CoCl4]2–, blue
23.85 (a)
(b) sodium dicarbonyltetracyanoferrate(II) (c) +2, 6 d-electrons (d) We expect the complex to be low spin. Cyanide (and carbonyl) are high on the spectrochemical series, which means the complex will have a large Δ splitting, characteristic of low-spin complexes.
23.91 (a) Yes, the oxidation state of Co is +3 in both complexes. (b) Compound A has SO42– outside the coordination sphere and coordinated Br–, so it forms a precipitate with BaCl2(aq) but not AgNO3(aq). Compound B has Br– outside the coordination sphere and coordinated SO42–, so it forms a precipitate with AgNO3(aq) but not BaCl2(aq). (c) Compounds A and B are coordination sphere isomers. (d) Both compounds are strong electrolytes.
23.94 The chemical formula is [Pd(NC5H5)2Br2]. This is an electrically neutral square-planar complex of Pd(II), a nonelectrolyte whose solutions do not conduct electricity. Because the dipole moment is zero, it must be the trans isomer.
23.96 47.3 mg Mg2+/L, 53.4 mg Ca2+/L
23.99 ΔE = 3.02 × 10–19 J/photon, λ = 657 nm. The complex will absorb in the visible around 660 nm and appear blue-green.
CHAPTER 24
24.1 Molecules (c) and (d) are the same molecule.
24.4 Compound (b), which has hydrogen bonding, has the highest boiling point.
24.7 (a) sp3 (b) sp2 (c) sp2 (d) sp
24.9 Numbering from the right on the condensed structural formula, C1 has trigonal-planar electrondomain geometry, 120° bond angles, and sp2 hybridization; C2 and C5 have tetrahedral electron-domain geometry, 109° bond angles, and sp3 hybridization; C3 and C4 have linear electron-domain geometry, 180° bond angles, and sp hybridization.
24.11 NH3 and CO are not typical organic molecules. NH3 contains no carbon atoms. Carbon monoxide contains a C atom that does not form four bonds.
24.13 (a) A straight-chain alkane has all carbon atoms connected in a continuous chain. A carbon atom is bound to no more than two other carbon atoms and forms only σ bonds. A branched-chain hydrocarbon has a branch; at least one carbon atom is bound to three or more carbon atoms. (b) An alkane is a complete molecule composed of carbon and hydrogen in which all bonds are σ bonds. An alkyl group is a substituent formed by removing a hydrogen atom from an alkane.
24.15 (a) 2-methylhexane (b) 4-ethyl-2, 4-dimethyldecane (c) CH3CH2CH2CH2CH2CH(CH3)2 (d) CH3CH2CH2CH2CH(CH2CH3) CH(CH3) CH(CH3)2
(e)
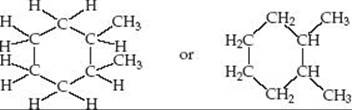
24.17 (a) 2, 3-dimethylheptane (b) CH3CH2CH2C(CH3)3
(c)
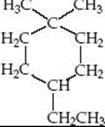
(d) 2, 2, 5-trimethylhexane (e) methylcyclobutane
24.19 65
24.21 (a) Alkanes are said to be saturated because they cannot undergo addition reactions, such as those characteristic of carbon-carbon double bonds. (b) No. The compound C4H6 does not contain the maximum possible number of hydrogen atoms and is unsaturated.
24.23 (a) C5H12 (b) C5H10 (c) C5H10 (d) C5H8; saturated: (a), (b); unsaturated: (c), (d)
24.25 One possible structure is ![]()
24.27 There are at least 46 structural isomers with the formula C6H10. A few of them are
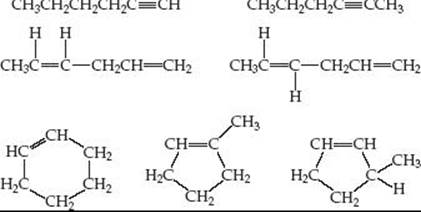
24.29
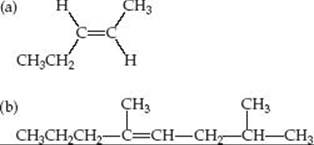
(c) cis-6-methyl-3-octene (d) para-dibromobenzene (e) 4, 4-dimethyl-1-hexyne
24.31 Geometric isomerism in alkenes is the result of restricted rotation about the double bond. In alkanes bonding sites are interchangeable by free rotation about the C — C single bonds. In alkynes there is only one additional bonding site on a triply bound carbon, so no isomerism results.
24.33 (a) No
(b)
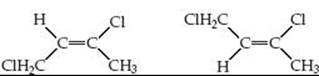
(c) no (d) no
24.35 (a) An addition reaction is the addition of some reagent to the two atoms that form a multiple bond. In a substitution reaction one atom or group of atoms replaces another atom. Alkenes typically undergo addition, while aromatic hydrocarbons usually undergo substitution.
(b)
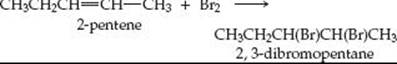
(c)
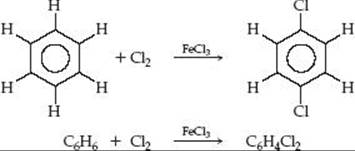
24.37 (a) The 60° C — C — C angles in the cyclopropane ring cause strain that provides a driving force for reactions that result in ring opening. There is no comparable strain in the five-or six-membered rings. (b) C2H4(g) + HBr(g) ![]() CH3CH2Br(l); C6H6(l) + CH3CH2Br(l)
CH3CH2Br(l); C6H6(l) + CH3CH2Br(l) ![]() C6H5CH2CH3(l) + HBr(g)
C6H5CH2CH3(l) + HBr(g)
24.39 Not necessarily. That the two rate laws are first order in both reactants and second order overall indicates that the activated complex in the rate-determining step in each mechanism is bimolecular and contains one molecule of each reactant. This is usually an indication that the mechanisms are the same, but it does not rule out the possibility of different fast steps or a different order of elementary steps.
24.41 ΔHcomb/mol CH2 for cyclopropane = 696.3 kJ, for cyclopentane = 663.4 kJ. ΔHcomb/CH2 group for cyclopropane is greater because C3H6 contains a strained ring. When combustion occurs, the strain is relieved and the stored energy is released.
24.43 (a) Alcohol (b) amine, alkene (c) ether (d) ketone, alkene (e) aldehyde (f) carboxylic acid, alkyne
24.45 (a) Propionaldehyde (or propanal):
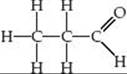
(b) ethylmethyl ether:
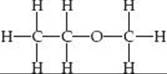
24.47 (a)
![]()
(b)
![]()
(c)
24.49
24.51
24.53 The presence of both —OH and — C ═ O groups in pure acetic acid leads us to conclude that it will be a strongly hydrogenbonded substance. That the melting and boiling points of pure acetic acid are both higher than those of water, a substance we know to be strongly hydrogen-bonded, supports this conclusion.
24.55 (a) CH3CH2CH2CH(OH) CH3 (b) CH3CH(OH) CH2OH
(c)
![]()
(d)
(e) CH3OCH2CH3
24.57
24.59 (a) An α -amino acid contains an NH2 group attached to the carbon adjacent to the carboxcylic acid function. (b) In protein formation, amino acids undergo a condensation reaction between the amino group of one molecule and the carboxylic acid group of another to form the amide linkage. (c) The bond that links amino acids in proteins is called the peptide bond.
24.61
24.63 (a)
(b) Three tripeptides ar possible: Gly-Gly-His, GGH; Gly-His-Gly, GHG; His-Gly-Gly, HGG
24.65 The primary structure of a protein refers to the sequence of amino acids in the chain. The secondary structure is the configuration (helical, folded, open) of the protein chain. The tertiary structure is the overall shape of the protein determined by the way the segments fold together. (b) X-ray crystallography is the primary and preferred technique for determining protein structure.
24.67 (a) Carbohydrates, or sugars, are polyhydroxyaldehydes or ketones composed of carbon, hydrogen, and oxygen. They are derived primarily from plants and are a major food source for animals. (b) A monosaccharide is a simple sugar molecule that cannot be decomposed into smaller sugar molecules by hydrolysis. (c) A disaccharide is a carbohydrate composed of two simple sugar units. Hydrolysis breaks a disaccharide into two monosaccharides. (d) A polysaccharide is a polymer composed of many simple sugar units.
24.69 The empirical formula of cellulose is C6H10O5. As in glycogen, the six-membered ring form of glucose forms the monomer unit that is the basis of the polymer cellulose. In cellulose, glucose monomer units are joined by β linkages.
24.71 (a) In the linear form of mannose, the aldehydic carbon is C1. Carbon atoms 2, 3, 4, and 5 are chiral because they each carry four different groups. (b) Both the α (left) and β (right) forms are possible.
24.73 Two important kinds of lipids are fats and fatty acids. Structurally, fatty acids are carboxylic acids with a hydrocarbon chain of more than four carbon atoms (typically 16–20 carbon atoms). Fats are esters formed by condensation of an alcohol, often glycerol, and a fatty acid. Phospholipids are glycerol esters formed from one phosphoric acid [RPO(OH)2] and two fatty acid (RCOOH) molecules. At body pH, the phosphate group is depronated and has a negative charge. The long, nonpolar hydrocarbon chains do not readily mix with water, but they do interact with the nonpolar chains of other phospholipid molecules to form the inside of a bilayer. The charged phosphate heads interact with polar water molecules on the outsides of the bilayer.
24.75 Purines, with the larger electron cloud and molar mass, will have larger dispersion forces than pyrimidines in aqueous solution.
24.77 5′ – TACG – 3′
24.79 The complimentary strand for 5′ – GCATTGGC–3′ is 3′ – CGTAACCG – 5′.
24.81
24.83
Cyclopentene does not show cis-trans isomerism because the existence of the ring demands that the C — C bonds be cis to one another.
24.86 (a) Aldehyde, trans-alkene, cis-alkene (b) ether, alcohol, alkene, amine (two of these, one aliphatic and one aromatic) (c) ketone (two of these), amine (two of these) (d) amide, alcohol (aromatic)
24.88 In a carboxylic acid, the electronegative carbonyl oxygen withdraws electron density from the O — H bond, rendering the bond more polar and the H more ionizable. And carboxylate anion is stabilized by resonance and encourages ionization of the carboxylic acid. In an alcohol no electronegative atoms are bound to the carbon that holds the — OH group, and the H is tightly bound to the O.
24.92 Glu-Cys-Gly is the only possible order. Glutamic acid has two carboxyl groups that can form a peptide bond with cysteine, so there are two possible structures for glutathione.
24.95 In both cases, stronger intermolecular forces lead to the higher boiling point. Ethanol contains O — H bonds, which form strong intermolecular hydrogen bonds, while dimethyl ether experiences only weak dipole–dipole and dispersion forces. The heavier and polar CH2F2 experiences dipole–dipole and stronger dispersion forces, while CH4 experiences only weaker dispersion forces.
24.97