CHEMISTRY THE CENTRAL SCIENCE
10 GASES
10.3 THE GAS LAWS
Four variables are needed to define the physical condition, or state, of a gas: temperature, pressure, volume, and amount of gas, usually expressed as number of moles. The equations that express the relationships among these four variables are known as the gas laws. Because volume is easily measured, the first gas laws to be studied expressed the effect of one of the variables on volume, with the remaining two variables held constant.
CHEMISTRY AND LIFE
BLOOD PRESSURE
When your blood pressure is measured, two values are reported, such as 120/80 (120 over 80). The first measurement is systolic pressure, the maximum pressure when the heart is pumping. The second is diastolic pressure, the pressure when the heart is in the resting part of its pumping cycle. The units associated with these pressure measurements are torr.
Blood pressure is measured using a pressure gauge attached to a closed, air-filled cuff applied like a tourniquet to the arm (
FIGURE 10.4). The pressure gauge may be a mercury manometer or related device. A small pump is used to increase the pressure in the cuff until it is above the systolic pressure and therefore prevents blood from flowing. The pressure inside the cuff is slowly reduced until blood just begins to pulse through the artery, and the person measuring the pressure hears, through a stethoscope, a characteristic sound. At this point the pressure in the cuff equals the pressure that the blood exerts inside the artery. Reading the gauge gives the systolic pressure. The pressure in the cuff is then reduced further until the blood flows freely, indicated by another characteristic sound. The pressure at this point is the diastolic pressure.
Hypertension is abnormally high blood pressure. The usual criterion is a blood pressure greater than 140/90, although recent studies suggest that health risks increase for systolic readings above 120. Hypertension significantly increases the workload on the heart and places a stress on the walls of the blood vessels throughout the body. These effects increase the risk of aneurysms, heart attacks, and strokes.
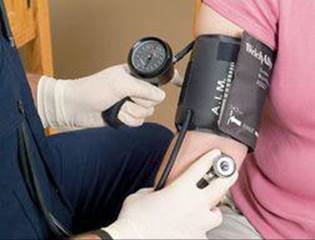
FIGURE 10.4 Measuring blood pressure.
GO FIGURE
Does atmospheric pressure increase or decrease as altitude increases? (Neglect changes in temperature.)
FIGURE 10.5 As a balloon rises in the atmosphere, its volume increases.
The Pressure–Volume Relationship: Boyle's Law
An inflated weather balloon released at Earth's surface expands as it rises (
FIGURE 10.5) because the pressure of the atmosphere decreases with increasing elevation. Thus, for our first pressure-volume relationship we can use our experience with balloons to say that gas volume increases as the pressure exerted on the gas decreases.
British chemist Robert Boyle (1627–1691) first investigated the relationship between the pressure of a gas and its volume, using a J-shaped tube like that shown in 
FIGURE 10.6. In the tube on the left, a quantity of gas is trapped above a column of mercury. Boyle then changed the pressure on the gas by adding mercury to the tube. He found that the volume of the gas decreased as the pressure increased. For example, doubling the pressure caused the gas volume to decrease to half its original value.
GO FIGURE
What is the total pressure on the gas after the 760 mm Hg has been added?
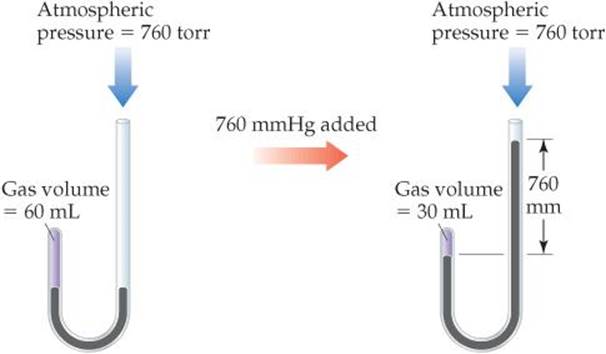
FIGURE 10.6 Boyle's experiment relating pressure and volume for a gas.
GO FIGURE
What would a plot of P versus 1/V look like for a fixed quantity of gas at a fixed temperature?
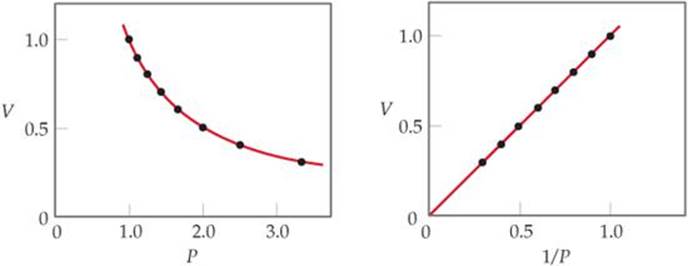
FIGURE 10.7 Boyle's Law. For a fixed quantity of gas at constant temperature, the volume of the gas is inversely proportional to its pressure.
Boyle's law, which summarizes these observations, states that the volume of a fixed quantity of gas maintained at constant temperature is inversely proportional to the pressure. When two measurements are inversely proportional, one gets smaller as the other gets larger. Boyle's law can be expressed mathematically as
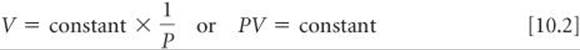
The value of the constant depends on temperature and on the amount of gas in the sample.
The graph of V versus P in FIGURE 10.7 shows the curve obtained for a given quantity of gas at a fixed temperature. A linear relationship is obtained when V is plotted versus 1/P as shown on the right in Figure 10.7.
Boyle's law occupies a special place in the history of science because Boyle was the first to carry out experiments in which one variable was systematically changed to determine the effect on another variable. The data from the experiments were then employed to establish an empirical relationship—a “law.”
We apply Boyle's law every time we breathe. The rib cage, which can expand and contract, and the diaphragm, a muscle beneath the lungs, govern the volume of the lungs. Inhalation occurs when the rib cage expands and the diaphragm moves downward. Both actions increase the volume of the lungs, thus decreasing the gas pressure inside the lungs. Atmospheric pressure then forces air into the lungs until the pressure in the lungs equals atmospheric pressure. Exhalation reverses the process—the rib cage contracts and the diaphragm moves up, decreasing the volume of the lungs. Air is forced out of the lungs by the resulting increase in pressure.
GIVE IT SOME THOUGHT
What happens to the pressure of a gas if you double its volume while its temperature is held constant?
The Temperature–Volume Relationship: Charles's Law
As 
FIGURE 10.8 illustrates, the volume of an inflated balloon increases when the temperature of the gas inside the balloon increases and decreases when the temperature of the gas decreases.
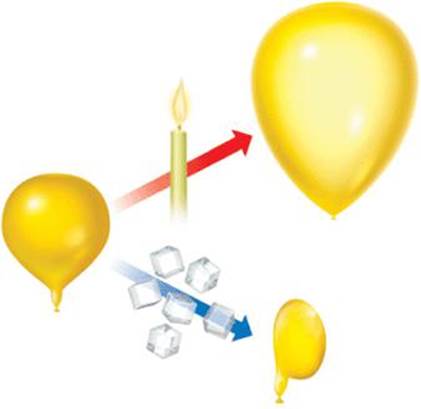
FIGURE 10.8 The effect of temperature on volume.
The relationship between gas volume and temperature—volume increases as temperature increases and decreases as temperature decreases—was discovered in 1787 by French scientist Jacques Charles (1746–1823). Some typical volume-temperature data are shown in FIGURE 10.9. Notice that the extrapolated (dashed) line passes through –273 °C. Note also that the gas is predicted to have zero volume at this temperature. This condition is never realized, however, because all gases liquefy or solidify before reaching this temperature.
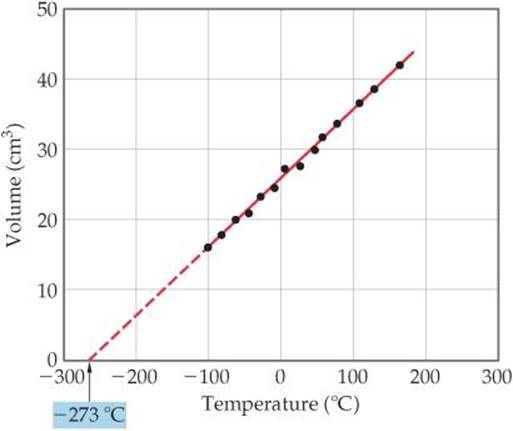
FIGURE 10.9 Charles's Law. For a fixed quantity of gas at constant pressure, the volume of the gas is proportional to its temperature.
In 1848 William Thomson (1824–1907), a British physicist whose title was Lord Kelvin, proposed an absolute-temperature scale, now known as the Kelvin scale. On this scale 0 K, called absolute zero, equals -273.15 °C. 
(Section 1.4) In terms of the Kelvin scale, Charles's lawstates: The volume of a fixed amount of gas maintained at constant pressure is directly proportional to its absolute temperature. Thus, doubling the absolute temperature causes the gas volume to double. Mathematically, Charles's law takes the form
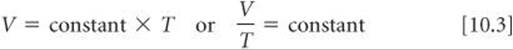
with the value of the constant depending on the pressure and on the amount of gas.
GIVE IT SOME THOUGHT
Does the volume of a fixed quantity of gas decrease to half its original value when the temperature is lowered from 100 °C to 50 °C?
The Quantity–Volume Relationship: Avogadro's Law
The relationship between the quantity of a gas and its volume follows from the work of Joseph Louis Gay-Lussac (1778–1823) and Amedeo Avogadro (1776–1856).
Gay-Lussac was one of those extraordinary figures in the history of science who could truly be called an adventurer. In 1804 he ascended to 23,000 ft in a hot-air balloon—an exploit that held the altitude record for several decades. To better control the balloon, Gay-Lussac studied the properties of gases. In 1808 he observed the law of combining volumes: At a given pressure and temperature, the volumes of gases that react with one another are in the ratios of small whole numbers. For example, two volumes of hydrogen gas react with one volume of oxygen gas to form two volumes of water vapor. (Section 3.1)
Three years later Amedeo Avogadro interpreted Gay-Lussac's observation by proposing what is now known as Avogadro's hypothesis : Equal volumes of gases at the same temperature and pressure contain equal numbers of molecules. For example, 22.4 L of any gas at 0 °C and 1 atm contain 6.02 × 1023 gas molecules (that is, 1 mol), as depicted in FIGURE 10.10.
GO FIGURE
How many moles of gas are in each vessel?
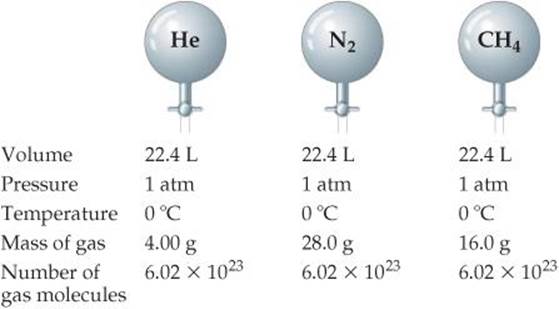
FIGURE 10.10 Avogadro's hypothesis. At the same volume, pressure, and temperature, samples of different gases have the same number of molecules but different masses.
Avogadro's law follows from Avogadro's hypothesis: The volume of a gas maintained at constant temperature and pressure is directly proportional to the number of moles of the gas. That is,
where n is number of moles. Thus, for instance, doubling the number of moles of gas causes the volume to double if T and P remain constant.
SAMPLE EXERCISE 10.3 Evaluating the Effects of Changes in P, V, n, and T on a Gas
Suppose we have a gas confined to a cylinder with a movable piston. (Sections 5.2, 5.3) Consider the following changes (assuming no leaks): (a) Heat the gas from 298 K to 360 K at constant pressure. (b) Reduce the volume from 1 L to 0.5 L at constant temperature. (c) Inject additional gas, keeping temperature and volume constant. Indicate how each change affects the average distance between molecules, the pressure of the gas, and the number of moles of gas in the cylinder.
SOLUTION
Analyze We need to think how each change affects (1) the distance between molecules, (2) the pressure of the gas, and (3) the number of moles of gas in the cylinder.
Plan We will use the gas laws and the general properties of gases to analyze each situation.
Solve
(a) Heating the gas while maintaining constant pressure will cause the piston to move and the volume to increase (Charles's law). Thus, the distance between molecules will increase. At constant pressure, obviously, the pressure will not change. The total number of moles of gas remains the same.
(b) Compressing the gas into a smaller volume does not change the total number of gas molecules; thus, the total number of moles remains the same. The average distance between molecules, however, must decrease because of the smaller volume. The reduction in volume causes the pressure to increase (Boyle's law).
(c) Injecting more gas into the cylinder while keeping the volume and temperature constant results in more molecules and, thus, an increase in the number of moles of gas in the cylinder. The average distance between molecules must decrease because their number per unit volume increases. Avogadro's law tells us that the volume of the cylinder should have increased when we added more gas, but here the volume is fixed. Boyle's law comes to our aid: If the volume is low, then pressure is high. Therefore, we expect that the pressure will increase in the cylinder if we inject more gas, keeping volume and temperature constant.
PRACTICE EXERCISE
Recall that density is mass per volume. (Section 1.4) What happens to the density of a gas as (a) the gas is heated in a constant-volume container; (b) the gas is compressed at constant temperature; (c) additional gas is added to a constant-volume container?
Answers: (a) no change, (b) increases, (c) increases