CONCEPTS IN BIOLOGY

PART II. CORNERSTONES: CHEMISTRY, CELLS, AND METABOLISM

2. The Basics of Life

2.9. Acids, Bases, and Salts

Acids, bases, and salts are three classes of biologically important compounds (table 2.3). Their characteristics are determined by the nature of their chemical bonds. Acids are ionic compounds that release hydrogen ions in solution. A hydrogen atom without its electron is a proton. You can think of an acid, then, as a substance able to donate a proton to a solution. Acids have a sour taste, such as that of citrus fruits. However, tasting chemicals to see if they are acids can be very hazardous, because many are highly corrosive. An example of a common acid is the phosphoric acid—H₃PO₄—in cola soft drinks. It is a dilute solution of this acid that gives cola drinks their typical flavor. Hydrochloric acid is another example:

Acids are ionically bonded molecules, which when placed in water dissociate, releasing hydrogen (H⁺) ions.

TABLE 2.3. Some Common Acids, Bases, and Salts

A base is the opposite of an acid, in that it is an ionic compound, which, when dissolved in water, removes hydrogen ions from solution. Bases, or alkaline substances, have a slippery feel on the skin. They have a caustic action on living tissue by converting the fats in living tissue into a water-soluble substance. A similar reaction is used to make soap by mixing a strong base with fat. This chemical reaction gives soap its slippery feeling. Bases are also used in alkaline batteries. Weak bases have a bitter taste—for example, the taste of broccoli, turnip, and cabbage. Many kinds of bases release a group of hydrogen ions known as a hydroxide ions, or an OH^- group. This group is composed of an oxygen atom and a hydrogen atom bonded together, but with an additional electron. The hydroxide ion is negatively charged; therefore, it will remove positively charged hydrogen ions from solution. A very strong base used in oven cleaners is sodium hydroxide, NaOH. Notice that ions that are free in solution are always written with the type and number of their electrical charge as a superscript.

Basic (alkaline) substances are ionically bonded molecules, which when placed in water dissociate, releasing hydroxide (OH^-) ions.

Acids and bases are also spoken of as being strong or weak (Outlooks 2.2). Strong acids (e.g., hydrochloric acid) are those that dissociate nearly all of their hydrogens when in solution. Weak acids (e.g., phosphoric acid) dissociate only a small percentage of their hydrogens. Strong bases dissociate nearly all of their hydroxides (NaOH); weak bases, only a small percentage. The weak base sodium bicarbonate, NaHCO₃, will react with acids in the following manner:

Notice that sodium bicarbonate does not contain a hydroxide ion but it is still a base, because it removes hydrogen ions from solution.

The degree to which a solution is acidic or basic is represented by a quantity known as pH. The pH scale is a measure of hydrogen ion concentration (figure 2.15). A pH of 7 indicates that the solution is neutral and has an equal number of H⁺ ions and OH^- ions to balance each other. As the pH number gets smaller, the number of hydrogen ions in the solution increases. A number higher than 7 indicates that the solution has more OH^- than H⁺. Pure water has a pH of 7. As the pH number gets larger, the number of hydroxide ions increases.

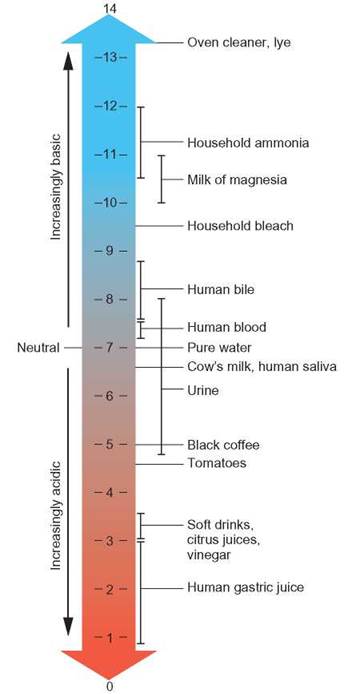
FIGURE 2.15. The pH Scale

The concentration of acid (proton donor or electron acceptor) is greatest when the pH number is lowest. As the pH number increases, the concentration of base (proton acceptor or electron donor) increases. At a pH of 7, the concentrations of H⁺ and OH^- are equal. As the pH number gets smaller, the solution becomes more acidic. As the pH number gets larger, the solution becomes more basic, or alkaline.

It is important to note that the pH scale is logarithmic—that is, a change in one pH number is actually a 10-fold change in real numbers of OH^- or H⁺. For example, there is 10 times more H⁺

When water dissociates, it releases both hydrogen (H⁺) and hydroxide (OH^-) ions. It is neither a base nor an acid. Its pH is 7, neutral.

in a solution of pH 5 than in a solution of pH 6 and 100 times more H⁺ in a solution of pH 4 than in a solution of pH 6.

Salts are ionic compounds that do not release either H⁺ or OH^- when dissolved in water; thus, they are neither acids nor bases. However, they are generally the result of the reaction between an acid and a base in a solution. For example, when an acid, such as HCl, is mixed with NaOH in water, the H⁺ and the OH^- combine with each other to form pure water, H₂O. The remaining ions (Na⁺ and Cl^-) join to form the salt NaCl:

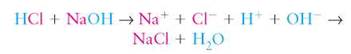
The chemical reaction that occurs when acids and bases react with each other is called neutralization. The acid no longer acts as an acid (it has been neutralized) and the base no longer acts as a base.

As you can see from figure 2.15, not all acids or bases produce the same pH. Some compounds release hydrogen ions very easily, cause low pHs, and are called strong acids. Hydrochloric acid (HCl) and sulfuric acid (H₂SO₄) are strong acids (figure 2.16a). Many other compounds give up their hydrogen ions grudgingly and therefore do not change pH very much. They are known as weak acids. Carbonic acid (H₂CO₃) and many organic acids found in living things are weak acids. Similarly, there are strong bases, such as sodium hydroxide (NaOH) and weak bases, such as sodium bicarbonate—Na⁺(HCO₃)^-.

FIGURE 2.16. Strong Acid and Strong Base

(a) Hydrochloric acid (HCl) has the common name of muriatic acid. It is a strong acid used in low concentrations to clean swimming pools and brick surfaces. It is important that you wear protective equipment when working with a solution of muriatic acid. (b) Liquid-Plumr^® is a good example of a drain cleaner with a strong base. The active ingredient is NaOH.

OUTLOOKS 2.2

Maintaining Your pH—How Buffers Work

Acids, bases, and salts are called electrolytes, because, when these compounds are dissolved in water, the solution of ions allows an electrical current to pass through it. Salts provide a variety of ions essential to the human body. Small changes in the levels of some ions can have major effects on the functioning of the body. The respiratory system and kidneys regulate many of the body's ions. Because many kinds of chemical activities are sensitive to changes in the pH of the surroundings, it is important to regulate the pH of the blood and other body fluids within very narrow ranges. Normal blood pH is about 7.4. Although the respiratory system and kidneys are involved in regulating the pH of the blood, there are several systems in the blood that prevent wide fluctuations in pH.

Buffers are mixtures of weak acids and the salts of weak acids that tend to maintain constant pH, because the mixture can either accept or release hydrogen ions (H⁺). The weak acid can release hydrogen ions (H⁺) if a base is added to the solution, and the negatively charged ion of the salt can accept hydrogen ions (H⁺) if an acid is added to the solution.

One example of a buffer system in the body is a phosphate buffer system, which consists of the weak acid dihydrogen phosphate (H₂PO₄^-) and the salt of the weak acid monohydrogen phosphate (HPO₄^-).

(The two arrows indicate that this is in balance, with equal reactions in both directions.) The addition of an acid to the mixture causes the equilibrium to shift to the left.

Notice that the arrow pointing to the right is shorter than the arrow pointing to the left. This indicates that H+ is combining with HPO₄^- and additional H₂PO₄^- is being formed. This removes the additional hydrogen ions from solution and ties them up in the H₂PO₄^-, so that the amount of free hydrogen ions in the solution remains constant.

Similarly, if a base is added to the mixture, the equilibrium shifts to the right, additional hydrogen ions are released to tie up the hydroxyl ions, and the pH remains unchanged.

Seawater is a buffer solution that maintains a pH of about 8.2. Buffers are also added to medicines and to foods. Many lemon-lime carbonated beverages, for example, contain citric acid and sodium citrate (salt of the weak acid), which forms a buffer in the acid range. The beverage label may say that these chemicals are to impart and regulate "tartness." In this case, the tart taste comes from the citric acid, and the addition of sodium citrate makes it a buffered solution.

2.9. CONCEPT REVIEW

24. What does it mean if a solution has a pH of 3, 12, 2, 7, or 9?

25. If the pH of a solution changes from 8 to 9, what happens to the hydroxide ion concentration?

Summary

The study of life involves learning about the structure and function of organisms. All organisms display the chemical and physical properties typical of all matter and energy. The two kinds of energy used by organisms are potential and kinetic. The kinetic molecular theory states that all matter is made up of tiny particles, which are in constant motion.

Energy can be neither created nor destroyed, but it can be converted from one form to another. Potential energy and kinetic energy can be interconverted. The amount of kinetic energy that the molecules of various substances contain determines whether they are solids, liquids, or gases. Temperature is a measure of the average kinetic energy of the molecules making up a substance. Heat is the total internal kinetic energy of molecules. The random motion of molecules, which is due to their kinetic energy, results in their being distributed throughout available space, forming mixtures.

There are many kinds of atoms, whose symbols and traits are described by the periodic table of the elements. These atoms differ from one another by the number of protons and electrons they contain. Each is given an atomic number, based on the number of protons in the nucleus, and an atomic weight, an average of all the isotopes of a particular element. The mass number is the sum of the number of protons and neutrons in the nucleus of an atom.

All matter is composed of atoms, which are composed of an atomic nucleus and electrons. The atomic nucleus can contain protons and neutrons, whereas the electrons encircle the nucleus at different energy levels. Atoms tend to seek their most stable configuration and follow the octet rule, which states that they all seek a filled outermost energy level.

Atoms may be combined by chemical reactions into larger units called molecules. There are many kinds of molecules. Two kinds of chemical bonds allow molecules to form—ionic bonds and covalent bonds. A third bond, the hydrogen bond, is a weaker bond that holds molecules together and may help large molecules maintain a specific shape. Molecules are described by their chemical formulas, which state the number and kinds of components of which they are composed.

An ion is an atom that is electrically unbalanced. Ions interact to form ionic compounds, such as acids, bases, and salts. Compounds that release hydrogen ions when mixed in water are called acids; those that remove hydrogen ions are called bases. A measure of the hydrogen ions present in a solution is the pH of the solution.

Water is one of the most important compounds required by all organisms. This polar molecule has many unique properties, which allow organisms to survive and reproduce. Without water, life as we know it on Earth would not be possible.

How atoms achieve stability is the nature of chemical reactions. Five of the most important chemical reactions that occur in organisms are (1) oxidation-reduction, (2) dehydration synthesis, (3) hydrolysis, (4) phosphorylation, and (5) acid-base reactions.

Acids, bases, and salts are three classes of biologically important molecules. The hydrogen ion releasing or acquiring properties of acids and bases make them valuable in all organisms.

Salts are a source of many essential ions. Although acids and bases may be potentially harmful, buffer systems help in maintain pH levels.

Basic Review

1. _____ is the total internal kinetic energy of molecules.

2. The atomic weight of the element sodium is

a. 22.989.

b. 11.

c. 10.252.

d. 11 + 22.989.

3. Which is not a pure substance?

a. the compound sugar

b. the element oxygen

c. a mixture of milk and honey

d. the compound table salt

4. When a covalent bond forms between two kinds of atoms that are the same, the result is known as a

a. mixture.

b. crystal.

c. dehydration chemical reaction.

d. diatomic molecule.

5. In this kind of chemical reaction, two molecules interact, resulting in the formation of a molecule of water and a new, larger end product.

a. hydrolysis

b. dehydration synthesis

c. phosphorylation

d. acid-base reaction

6. Which of the following is an acid?

a. HCl

b. NaOH

c. KOH

d. CaCO₃

7. Salts are compounds that do not release either _____ or _____ ions when dissolved in water.

8. This intramolecular force under the right conditions can result in a molecule that is coiled or twisted into a complex, three-dimensional shape.

a. covalent bond

b. ionic bond

c. hydrogen bond

d. cement bond

9. A triple covalent bond is represented by which of the following?

a. a single, fat, straight line

b. a single, thin, straight line

c. three separate, thin lines

d. three thin, curved lines

10. Electron clouds, or routes, traveled by electrons are sometimes drawn as spherical or _____ shapes.

11. Atoms of the same element differ from ions of that element because

a. they have different numbers of electrons.

b. their proton numbers are not the same.

c. their neutrons numbers are not the same.

d. there is no difference between an atom and an ion of the same element.

12. When someone uses the expression “you’re full of hot air,” he is referring to which phase of matter?

a. solid

b. liquid

c. gas

d. hydrogen

13. When a person is “running a fever,” she is experiencing an increase in her body’s _____.

14. Ions that are bonded together and form a threedimensional structure are called a _____.

15. A bottle of soda or pop is best described as

a. a heterogeneous mixture.

b. a compound.

c. a homogeneous mixture.

d. a pure substance.

Answers

1. Heat 2. a 3. c 4. d 5. b 6. a 7. H⁺, OH^- 8. C 9. c 10. hourglass 11. a 12. c 13. temperature 14. crystal 15. C

Thinking Critically

Chemicals Around the House

Sodium bicarbonate (NaHCO₃) is a common household chemical known as baking soda, bicarbonate of soda, or bicarb. It has many uses and is a component of many products, including toothpaste and antacids, swimming pool chemicals, and headache remedies. When baking soda comes in contact with hydrochloric acid, the following reaction occurs:

What happens to the atoms in this reaction? In your description, include changes in chemical bonds, pH, and kinetic energy. Why is baking soda such an effective chemical in the previously mentioned products? Try this at home: Place a pinch of sodium bicarbonate (NaHCO₃) on a plate. Add two drops of vinegar. Observe the reaction. Based on the previous reaction, can you explain chemically what has happened?