Biology For Dummies
Part I Biology Basics
Chapter 4
The Living Cell
In This Chapter
Finding out what makes cells the basic units of life
Taking a look at the structure of prokaryotic and eukaryotic cells
Discovering how enzymes accelerate reactions
Every living thing has cells. The smallest creatures have only one, yet they’re as alive as you are. What exactly is a cell? In plain and simple terms, it’s the smallest living piece of an organism — including you. Without cells, you’d be a disorganized blob of chemicals that’d just ooze out into the environment. And that is why the cell is the fundamental unit of life.
You get to explore the purpose and structure of cells in this chapter. And because cells rely on chemical reactions to make things happen, you also find out all about enzymes, which are proteins that help speed up the pace of chemical reactions.
An Overview of Cells
Cells are sacs of fluid that are reinforced by proteins and surrounded by membranes. Inside the fluid float chemicals and organelles, structures inside cells that are used during metabolic processes. (Yes, an organism contains parts that are smaller than a cell, but these structures can’t perform all the functions of life on their own, so they aren’t considered to be alive.)
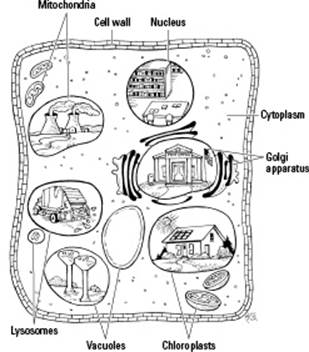
 A cell is the smallest part of an organism that retains characteristics of the entire organism. For example, a cell can take in fuel, convert it to energy, and eliminate wastes, just like the organism as a whole can. Because cells can perform all the functions of life (as shown in Figure 4-1), the cell is the smallest unit of life.
A cell is the smallest part of an organism that retains characteristics of the entire organism. For example, a cell can take in fuel, convert it to energy, and eliminate wastes, just like the organism as a whole can. Because cells can perform all the functions of life (as shown in Figure 4-1), the cell is the smallest unit of life.
Figure 4-1: Cells perform all the functions of life.
Cells can be categorized in different ways, according to structure or function, or in terms of their evolutionary relationships. In terms of structure, scientists categorize cells based on their internal organization:
Prokaryotes don’t have a “true” nucleus in their cells. Nor do they have organelles. Bacteria and archaea are all prokaryotes.
Eukaryotes have a nucleus in their cells that houses their genetic material. They also have organelles. Plants, animals, algae, and fungi are all eukaryotes.
Viruses versus bacteria
Viruses (like those that cause the flu, a cold, or AIDS) aren’t made of cells. Although viruses make you sick, just like bacteria do, viruses and bacteria are actually quite different. Viruses are simpler than bacteria and are made of just a few molecules. In fact, viruses have so few parts that they can’t even grow and divide by themselves (so they’re not considered to be alive). Viruses can only reproduce if they take over a host cell and steal its energy and materials (head to Chapter 17 for the details of how viruses attack cells).
Peeking at Prokaryotes
Prokaryotes include cells you’ve probably heard of, such as the bacteria E. coli and Streptococcus (which causes strep throat), the blue-green algae that occasionally cause lake closures, and the live cultures of bacteria in yogurt, as well as some cells you may never have heard of, called archaeans (see Chapter 10 for more on archaeans).
Whether you’ve heard of a specific prokaryote or not, you’re likely well aware that bacteria have a pretty bad rap. They seem to make the papers only when they’re causing problems, such as disease. Behind the scenes, though, bacteria are quietly performing many beneficial tasks for people and the rest of life on planet Earth. Why, if bacteria could get some good headlines, those headlines might read a little something like this:
Bacteria are used in human food production! Yogurt and cheese are quite tasty, humans say.
Bacteria can clean up our messes! Oil-eating bacteria help save beaches, and other bacteria help clean up our sewage.
Normal body bacteria help prevent disease! Bacteria living on the body can prevent disease-causing bacteria from moving in.
Bacteria are nature’s recyclers! Bacteria release nutrients from dead matter during decomposition.
Bacteria help plants grow! Nitrogen-fixing bacteria can pull nitrogen out of the air and convert it to a form that plants can use.
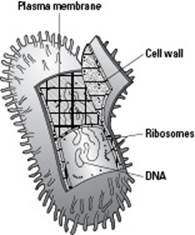
The cells of prokaryotes are fairly simple in terms of structure because they don’t have internal membranes or organelles like eukaryotic cells do (we cover all the structures present in eukaryotic cells later in this chapter). The majority of prokaryotic cells (like the one in Figure 4-2) share these characteristics:
A plasma membrane forms a barrier around the cell, and a rigid cell wall outside the plasma membrane provides additional support to the cell.
DNA, the genetic material of prokaryotes, is located in the cytoplasm, in an area called the nucleoid.
Ribosomes make proteins in the cytoplasm.
Prokaryotes break down food using cellular respiration (which requires oxygen, as explained in Chapter 5) and another type of metabolism called fermentation (which doesn’t require oxygen).
Figure 4-2: A prokaryotic cell.
Examining the Structure of Eukaryotic Cells
The living things you’re probably most familiar with — humans, animals, plants, mushrooms, and molds — are all eukaryotes, but they’re not the only members of the eukaryote family. Eukaryotes also include many inhabitants of the microbial world, such as algae, amoebas, and plankton.
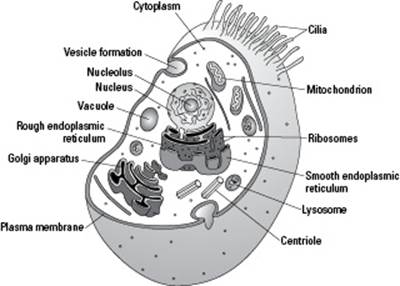
Eukaryotes have the following characteristics (see Figures 4-3 and 4-4 for diagrams of eukaryotic cells):
A nucleus that stores their genetic information.
A plasma membrane that encloses the cell and separates it from its environment.
Internal membranes, such as the endoplasmic reticulum and the Golgi apparatus, that create specialized compartments inside the cells.
A cytoskeleton made of proteins that reinforces the cells and controls cellular movements.
Organelles called mitochondria that combine oxygen and food to transfer the energy from food to a form that cells can use.
Organelles called chloroplasts, which use energy from sunlight plus water and carbon dioxide to make food. (Chloroplasts are found only in the cells of plants and algae.)
A rigid cell wall outside of their plasma membrane. (This is found only in the cells of plants, algae, and fungi; animal cells just have a plasma membrane, which is soft.)
Figure 4-3:Structures in a typical plant cell.
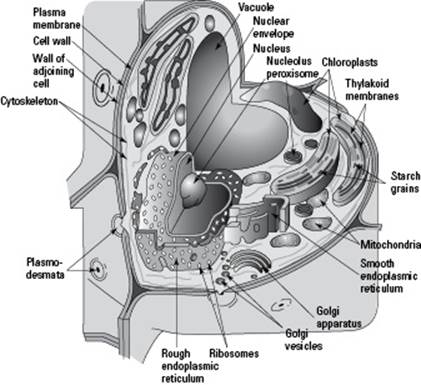
Figure 4-4:Structures in a typical animal cell.
Cells and the Organelles: Not a Motown Doo-wop Group
Your body is made of organs, which are made of tissues, which are made of cells. Just like you have organs that perform specific functions for your body, cells have organelles that perform specific functions for the cell. Some organelles are responsible for metabolizing food; others are responsible for making the structures the cell needs to function.
The sections that follow highlight the organelles found in eukaryotic cells and get you acquainted with their specific functions.
 Plant and animal cells are very similar, but they have a few significant differences in their organelles. Plant cells have chloroplasts, large central vacuoles, and cell walls; animal cells don’t. What animal cells do have that plant cells don’t are centrioles, small structures that are part of the cytoskeleton and appear during animal cell division.
Plant and animal cells are very similar, but they have a few significant differences in their organelles. Plant cells have chloroplasts, large central vacuoles, and cell walls; animal cells don’t. What animal cells do have that plant cells don’t are centrioles, small structures that are part of the cytoskeleton and appear during animal cell division.
Holding it all together: The plasma membrane
The membrane that encloses and defines all cells as separate from their environment is called the plasma membrane, or the cell membrane. The job of the plasma membrane is to separate the chemical reactions occurring inside the cell from the chemicals outside the cell.
 Thinking of the plasma membrane as an international border controlling what enters and leaves a particular country is a good way of remembering the plasma membrane’s function.
Thinking of the plasma membrane as an international border controlling what enters and leaves a particular country is a good way of remembering the plasma membrane’s function.
The fluid inside a cell, called the cytoplasm, contains all the organelles and is very different from the fluid found outside the cell. (Cyto means “cell,” and plasm means “shape.” So, cytoplasm literally means “cell shape,” which is fitting because the plasma membrane is what defines cell shape.)
Animal cells are supported by a fluid protein-and-carbohydrate matrix called the extracellular matrix. (Extra means “outside,” so extracellular literally means “outside the cell.”) Plant cells are supported by a more solid structure, called a cell wall, that’s made of the carbohydrate cellulose.
The next sections explain the structure of the plasma membrane in detail and describe how materials move through it in order to keep the cell healthy and allow it to do its job.
Deciphering the fluid-mosaic model
Plasma membranes are made of several different components, much like a mosaic work of art. Because membranes are a mosaic, and because they’re flexible and fluid, scientists call the description of membrane structure the fluid-mosaic model. We’ve drawn the model for you in Figure 4-5 to help you visualize all the parts that make up a plasma membrane.
Moving from the left of Figure 4-5 to the right, notice the phospholipid bilayer. This serves as the foundation of the plasma membrane. Phospholipids are a special kind of lipid (see Chapter 3 for more on lipids); they have water-attracting and water-repelling parts. At body temperature, phospholipids have the consistency of thick vegetable oil, which allows plasma membranes to be flexible and fluid. Each phospholipid molecule has a hydrophilic head that’s attracted to water and a hydrophobic tail that repels water. (Hydro means “water,” phile means “love,” andphobia means “fear,” so hydrophilic literally means “water-loving” and hydrophobic literally means “water-fearing.”)
Figure 4-5: The fluid-mosaic model of plasma membranes.
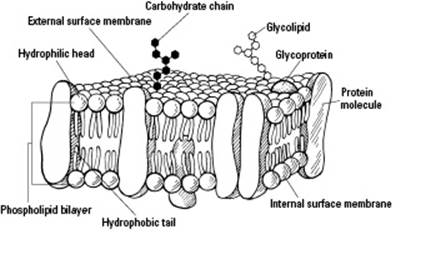
 In each cell, the hydrophilic heads point toward the watery environments outside and inside the cell, sandwiching the hydrophobic tails between them to form the phospholipid bilayer (see Figure 4-5). Because cells reside in a watery solution (the extracellular matrix), and because they contain a watery solution inside of them (cytoplasm), the plasma membrane forms a sphere around each cell so that the water-attracting heads are in contact with the fluid, and the water-repelling tails are protected on the inside.
In each cell, the hydrophilic heads point toward the watery environments outside and inside the cell, sandwiching the hydrophobic tails between them to form the phospholipid bilayer (see Figure 4-5). Because cells reside in a watery solution (the extracellular matrix), and because they contain a watery solution inside of them (cytoplasm), the plasma membrane forms a sphere around each cell so that the water-attracting heads are in contact with the fluid, and the water-repelling tails are protected on the inside.
In addition to phospholipids, proteins are a major component of plasma membranes. The proteins are embedded in the phospholipid bilayer, but they can drift in the membrane like ships sailing through an oily ocean.
Cholesterol and carbohydrates are minor components of plasma membranes, but they play fairly significant roles.
Cholesterol makes the membrane more stable and prevents it from solidifying when your body temperature is low. (It keeps you from literally freezing when you’re “freezing.”)
Carbohydrate chains attach to the outer surface of the plasma membrane on each cell. When carbohydrates attach to the phospholipids, they form glycolipids (and when they attach to the proteins, they form glycoproteins). Your DNA determines which specific carbohydrates attach to your cells, affecting characteristics such as your blood type.
Transporting materials through the plasma membrane
Cells are busy places. They manufacture materials that need to be shipped out, and they need to take up materials such as food and signals. These important exchanges take place at the plasma membrane.
Whether or not a molecule can cross a plasma membrane depends upon its structure and the cell. Small, hydrophobic molecules such as oxygen and carbon dioxide are compatible with the hydrophobic tails of the phosopholipid bilayer, so they can easily scoot across membranes. Hydrophilic molecules such as ions can’t get through the tails by themselves, so they need help to cross. Larger molecules (think food and hormones) also need help, which comes in the form of transport proteins.
Some of these proteins help form openings called channels in the membrane. Small molecules such as hormones and ions may be allowed to pass through these channel proteins. Other proteins, called carrier proteins, pick up molecules on one side of a membrane and then drop them off on the other side. Other proteins in the membrane act as receptors that detect the presence of molecules the cell needs. When these molecules bind to receptors, the cell allows the molecules to cross the plasma membrane with the help of transport proteins.
 Because the plasma membrane is choosy about what substances can pass through it, it’s said to be selectively permeable. (Permeability describes the ease with which substances can pass through a border, such as a cell membrane. Permeable means that most substances can easily pass through. Impermeable means substances can’t pass through. Selectively permeable and semipermeable mean that only certain substances are able to pass through.)
Because the plasma membrane is choosy about what substances can pass through it, it’s said to be selectively permeable. (Permeability describes the ease with which substances can pass through a border, such as a cell membrane. Permeable means that most substances can easily pass through. Impermeable means substances can’t pass through. Selectively permeable and semipermeable mean that only certain substances are able to pass through.)
Materials can pass through the plasma membrane either passively or actively, as you discover in the following sections.
Passively moving along
Passive transport requires no energy on the part of the cell. Molecules can move passively across membranes in one of two ways. In both cases, the molecules are moving from where they’re more concentrated to where they’re less concentrated. (In other words, they spread themselves out randomly until they’re evenly distributed.) Here are the two methods of passive transport:
Diffusion: The movement of molecules other than water from an area where they’re highly concentrated to an area where they’re less concentrated is diffusion. To go from a high concentration to a low concentration, the molecules need only diffuse (spread themselves) across the membrane, separating the areas of concentration.
Osmosis: The diffusion of water across a membrane is osmosis. It works the same way as diffusion, but it can be a little confusing because the movement of water is affected by the concentration of substances called solutes that are dissolved in the water. Basically, water moves from areas where it’s more concentrated (more pure) to areas where it’s less concentrated (where it has more solutes).
 Try thinking about osmosis in terms of the solutes: Water moves toward the area with the greatest concentration of solutes. For example, the blood in your body contains a certain amount of salt. If the concentration of salt in your blood suddenly rises, water moves out of the blood cells, and your blood cells shrivel up. On the other hand, if too much fluid is in the bloodstream, the blood cells have too many molecules of salt in comparison, so they take in water. If they need to take in too much water to bring everything back into balance, they can swell and burst.
Try thinking about osmosis in terms of the solutes: Water moves toward the area with the greatest concentration of solutes. For example, the blood in your body contains a certain amount of salt. If the concentration of salt in your blood suddenly rises, water moves out of the blood cells, and your blood cells shrivel up. On the other hand, if too much fluid is in the bloodstream, the blood cells have too many molecules of salt in comparison, so they take in water. If they need to take in too much water to bring everything back into balance, they can swell and burst.
 The relative concentration of solutes on either side of a membrane is compared in terms of the tonicity of the solutions. If a solution is isotonic, the concentrations of the substances (solutes) and water (solvent) on both sides of the membrane are equal. If one solution is hypotonic,it has a lower concentration of substances (and more water) in it when compared to another solution. If a solution is hypertonic, it has a higher concentration of substances in it (and less water) when compared to another solution.
The relative concentration of solutes on either side of a membrane is compared in terms of the tonicity of the solutions. If a solution is isotonic, the concentrations of the substances (solutes) and water (solvent) on both sides of the membrane are equal. If one solution is hypotonic,it has a lower concentration of substances (and more water) in it when compared to another solution. If a solution is hypertonic, it has a higher concentration of substances in it (and less water) when compared to another solution.
Actively helping molecules across
Active transport requires some energy from the cell to move molecules that can’t cross the phospholipid bilayer on their own from where they’re less concentrated to where they’re more concentrated. Carrier proteins, called active transport proteins or pumps, use energy stored in the cell to concentrate molecules inside or outside of the cell.
 Active transport is a little like having to pay to take the Staten Island Ferry. The ferry is the carrier protein, and you’re the big molecule that needs help getting from the bloodstream (New York Bay) to the inside of the cell (New York City). The fee that you pay is equivalent to the energy molecules expended by the cell.
Active transport is a little like having to pay to take the Staten Island Ferry. The ferry is the carrier protein, and you’re the big molecule that needs help getting from the bloodstream (New York Bay) to the inside of the cell (New York City). The fee that you pay is equivalent to the energy molecules expended by the cell.
Diffusion at work in your lungs
In the human body, one place that diffusion occurs is in the lungs. You breathe in air, and oxygen gets into the tiniest air sacs of the lungs, called the alveoli. Surrounding the alveoli are the tiniest blood vessels — the pulmonary capillaries. The pulmonary capillaries contain the lowest concentration of oxygen in the body because by the time blood gets to them, most of the oxygen has been used up by other organs and tissues. This means the alveoli have a higher concentration of oxygen than the pulmonary capillaries. Oxygen from the alveoli of the lungs diffuses across the membrane between the air sac and the capillary, getting into the bloodstream so it can travel around the body.
Supporting the cell: The cytoskeleton
Much like your skeleton reinforces the structure of your body, the cytoskeleton of a cell reinforces that cell’s structure. However, it provides that reinforcement in the form of protein cables rather than bones. The proteins of the cytoskeleton reinforce the plasma membrane and the nuclear envelope (covered in the next section). They also run through the cell like railroad tracks, helping vesicles and organelles circulate around the cell.
 Think of the cytoskeleton as a cell’s scaffolding and railroad tracks because it reinforces the cell and allows things to move around within it.
Think of the cytoskeleton as a cell’s scaffolding and railroad tracks because it reinforces the cell and allows things to move around within it.
 Some cells have whiplike projections that help them swim or move fluids. If the projections are short, like those shown in Figure 4-4, the structures are called cilia. If the projections are long, they’re called flagella. Both cilia and flagella contain cytoskeletal proteins. The proteins flex back and forth, making the cilia and flagella beat like little whips. Cells with cilia exist in your respiratory tract, where they wiggle their cilia to move mucus so you can cough it out; they’re also found in your digestive tract, where they help move food along. Flagella are present on human sperm cells; they’re what allow sperm to swim rapidly toward an egg during sexual reproduction.
Some cells have whiplike projections that help them swim or move fluids. If the projections are short, like those shown in Figure 4-4, the structures are called cilia. If the projections are long, they’re called flagella. Both cilia and flagella contain cytoskeletal proteins. The proteins flex back and forth, making the cilia and flagella beat like little whips. Cells with cilia exist in your respiratory tract, where they wiggle their cilia to move mucus so you can cough it out; they’re also found in your digestive tract, where they help move food along. Flagella are present on human sperm cells; they’re what allow sperm to swim rapidly toward an egg during sexual reproduction.
Controlling the show: The nucleus
Every cell of every living thing contains genetic material called DNA (which is short for deoxyribonucleic acid, as explained in Chapter 3). In eukaryotic cells, DNA is contained within a chamber called a nucleus that’s separated from the cytoplasm by a membrane called the nuclear envelope (also known as the nuclear membrane). In the nucleus of cells that aren’t multiplying, the DNA is wound around proteins and loosely spread out in the nucleus. When DNA is in this form, it’s called chromatin. However, right before a cell divides, the chromatin coils up tightly into chromosomes. Human cells have 46 chromosomes, each one of which is a separate piece of DNA.
 DNA contains the instructions for building molecules, mostly proteins, that do the work of the cell. Cell function depends upon the action of these proteins, and organism function depends on cell function. So, ultimately, organism function depends upon the instructions in the DNA.
DNA contains the instructions for building molecules, mostly proteins, that do the work of the cell. Cell function depends upon the action of these proteins, and organism function depends on cell function. So, ultimately, organism function depends upon the instructions in the DNA.
 Consider the nucleus the library of the cell because it holds lots of information. The chromosomes are the library’s books, full of instructions for building cells.
Consider the nucleus the library of the cell because it holds lots of information. The chromosomes are the library’s books, full of instructions for building cells.
Proteins in the nucleus copy the instructions from the DNA into molecules that get shipped out to the cytoplasm, where they direct the behavior of the cell. For example, each nucleus has a round mass inside it called a nucleolus. The nucleolus produces ribosomes, which move out to the cytoplasm to help make proteins. In experiments where scientists transplant the nucleus from one cell into the cytoplasm of another cell, the cell behaves according to the instructions in the nucleus. So, the nucleus is the true control center of the cell.
Creating proteins: Ribosomes
Ribosomes are small structures found in the cytoplasm of cells. The instructions for proteins are copied from the DNA into a new molecule called messenger RNA (mRNA). The mRNA leaves the nucleus and carries the instructions to the ribosomes out in the cytoplasm of the cell. The ribosomes then organize the mRNA and other molecules that are needed to build proteins (for the full scoop on how proteins are made, flip to Chapter 8).
 Thinking of ribosomes like workbenches where proteins are built is a good way to remember their function.
Thinking of ribosomes like workbenches where proteins are built is a good way to remember their function.
Serving as the cell’s factory: The endoplasmic reticulum
The endoplasmic reticulum (ER) is a series of canals that connects the nucleus to the cytoplasm of the cell. (Endo means “inside,” and reticulum refers to the netlike appearance of the ER, so endoplasmic reticulum basically means “a netlike shape inside the cytoplasm.”) As you can see in Figure 4-4, part of the ER is covered in dots, which are actually ribosomes that attach to it during the synthesis of certain proteins. This part is called the rough ER, or RER. The part of the ER without ribosomes is called the smooth ER (SER).
Ribosomes on the RER make proteins that either get shipped out of the cell or become part of the membrane. (Proteins that stay in the cell are put together on ribosomes that float free in the cytoplasm.) The SER is involved in the metabolism of lipids (fats). Proteins and lipids made at the ER get packaged up into little spheres of membrane called transport vesicles that carry the molecules from the ER to the nearby Golgi apparatus.
 To help you remember the ER’s purpose, think of the ER as the cell’s internal manufacturing plant because it produces proteins and lipids and then ships them out (to the Golgi apparatus).
To help you remember the ER’s purpose, think of the ER as the cell’s internal manufacturing plant because it produces proteins and lipids and then ships them out (to the Golgi apparatus).
Preparing products for distribution: The Golgi apparatus
The Golgi apparatus, which is located very close to the ER (as you can see in Figure 4-4), looks like a maze with water droplets splashing off of it. The “water droplets” are transport vesicles bringing material from the ER to the Golgi apparatus.
Inside the Golgi apparatus, products produced by the cell, such as hormones or enzymes, are chemically tagged and packaged for export either to other organelles or to the outside of the cell. After the Golgi apparatus has processed the molecules, it packages them back up into a vesicle and ships them out again. If the molecules are to be shipped out of the cell, the vesicle finds its way to the plasma membrane, where certain proteins allow a channel to be produced so that the products inside the vesicle can be secreted to the outside of the cell. Once outside the cell, the materials can enter the bloodstream and be transported through the body to where they’re needed.
 If it helps you remember, you can consider the Golgi apparatus the cell’s post office because it receives molecular packages and tags them for shipping to their proper destination.
If it helps you remember, you can consider the Golgi apparatus the cell’s post office because it receives molecular packages and tags them for shipping to their proper destination.
Cleaning up the trash: Lysosomes
Lysosomes are special vesicles formed by the Golgi apparatus to clean up the cell. Lysosomes contain digestive enzymes, which are used to break down products that may be harmful to the cell and “spit” them back out into the extracellular fluid. (We fill you in on enzymes in the later “Presenting Enzymes, the Jump-Starters” section.) Lysosomes also remove dead organelles by surrounding them, breaking down their proteins, and releasing them to construct a new organelle.
 Essentially, lysosomes are the waste collectors of the cell; they gather materials the cell no longer needs and break them down so some parts can be recycled.
Essentially, lysosomes are the waste collectors of the cell; they gather materials the cell no longer needs and break them down so some parts can be recycled.
Destroying toxins: Peroxisomes
Peroxisomes are little sacs of enzymes that break down many different types of molecules and help protect the cell from toxic products. Peroxisomes help in the breakdown of lipids, making their energy available to the cell.
Some of the reactions that occur in peroxisomes produce hydrogen peroxide, which is a dangerous molecule to cells. Peroxisomes prevent your cells from being damaged by hydrogen peroxide by converting the hydrogen peroxide into plain old water plus an extra oxygen molecule, both of which are always needed by the body and can be used in any cell.
 Peroxisomes are a little bit like food processors. They’re involved in breaking things down, just like the blades of a food processor are used to chop up larger pieces of food.
Peroxisomes are a little bit like food processors. They’re involved in breaking things down, just like the blades of a food processor are used to chop up larger pieces of food.
Providing energy, ATP-style: Mitochondria
Mitochondria supply cells with the energy they need to move and grow by breaking down food molecules, extracting their energy, and transferring it to an energy-storing molecule that cells can easily use. That energy-storing molecule is ATP, short for adenosine triphosphate.
 Recall the role of mitochondria by thinking of them as the power plants of the cell because they produce the energy the cell needs.
Recall the role of mitochondria by thinking of them as the power plants of the cell because they produce the energy the cell needs.
 The process mitochondria use to transfer the energy in foods to ATP is called cellular respiration. What occurs during cellular respiration is like what occurs when a campfire burns, just on a much smaller scale. In a campfire, wood burns, consuming oxygen and transferring energy (heat and light) and matter (carbon dioxide and water) to the environment. In a mitochondrion, food molecules break down, consuming oxygen and transferring energy to cells (to be stored in ATP) and the environment (as heat). For more details on cellular respiration, see Chapter 5.
The process mitochondria use to transfer the energy in foods to ATP is called cellular respiration. What occurs during cellular respiration is like what occurs when a campfire burns, just on a much smaller scale. In a campfire, wood burns, consuming oxygen and transferring energy (heat and light) and matter (carbon dioxide and water) to the environment. In a mitochondrion, food molecules break down, consuming oxygen and transferring energy to cells (to be stored in ATP) and the environment (as heat). For more details on cellular respiration, see Chapter 5.
Converting energy: Chloroplasts
Chloroplasts are organelles found solely in plants and algae. They specialize in transferring energy from the Sun into the chemical energy in food. They often have a distinctly green color because they contain chlorophyll, a green pigment that can absorb sunlight. During photosynthesis, the energy from sunlight is used to combine the atoms from carbon dioxide and water to produce sugars, from which all types of food molecules can be made. (Turn to Chapter 5 for more on photosynthesis.)
 Consider chloroplasts the plant equivalent of solar-powered kitchens because they use energy from the Sun and “ingredients” from the environment (carbon dioxide and water) to make food.
Consider chloroplasts the plant equivalent of solar-powered kitchens because they use energy from the Sun and “ingredients” from the environment (carbon dioxide and water) to make food.
 A very common misconception is that plants have chloroplasts rather than mitochondria. The truth is, plants have both! Think about it — it wouldn’t do plants much good to make food if they couldn’t also break it down. When plants make food, they store matter and energy for later. When they need the matter and energy, they use their mitochondria to break the food down into usable energy.
A very common misconception is that plants have chloroplasts rather than mitochondria. The truth is, plants have both! Think about it — it wouldn’t do plants much good to make food if they couldn’t also break it down. When plants make food, they store matter and energy for later. When they need the matter and energy, they use their mitochondria to break the food down into usable energy.
Presenting Enzymes, the Jump-Starters
Chemical reactions occur whenever the molecules in cells change. They’re usually part of a cycle or pathway that has separate reactions at each step. Of course, because the pace of life in cells is so fast, cells can’t just wait around for chemical reactions to happen — they have to make them happen quickly. Fortunately, they have the perfect tool at their disposal in the form of proteins called enzymes.
 Each reaction of a pathway or cycle requires a specific enzyme to act as a catalyst, something that speeds up the rate of chemical reactions. These proteins are folded in just the right way to do a specific job. Enzymes also have pockets, called active sites, that they use to attach to certain molecules. The molecule an enzyme binds to is called its substrate (see Figure 4-6).
Each reaction of a pathway or cycle requires a specific enzyme to act as a catalyst, something that speeds up the rate of chemical reactions. These proteins are folded in just the right way to do a specific job. Enzymes also have pockets, called active sites, that they use to attach to certain molecules. The molecule an enzyme binds to is called its substrate (see Figure 4-6).
Figure 4-6:Enzyme catalysis.
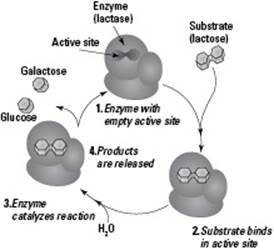
Without the specific enzyme necessary to catalyze a particular reaction, the cycle or pathway can’t be completed. The result of an uncompleted cycle or pathway is the lack of what that cycle or pathway is supposed to produce (a product). Without a needed product, a function can’t be performed, which negatively affects the organism. For example, if people don’t get enough vitamin C, the enzymes needed to make collagen can’t function, resulting in a disease called scurvy. The lack of collagen in people with scurvy causes bleeding gums, loss of teeth, and abnormal bone development in children.
The sections that follow introduce you to how enzymes work, what they need to get the job done, and how cells are able to keep them under control.
Staying the same . . .
 Enzymes themselves are recycled. They’re the same at the end of a reaction as they were at the beginning, and they can do their job again. For example, the first enzymatic reaction discovered was the one that breaks down urea into products that can be excreted from the body. The enzyme urease catalyzes the reaction between the reactants urea and water, yielding the products carbon dioxide and ammonia, which can be excreted easily by the body.
Enzymes themselves are recycled. They’re the same at the end of a reaction as they were at the beginning, and they can do their job again. For example, the first enzymatic reaction discovered was the one that breaks down urea into products that can be excreted from the body. The enzyme urease catalyzes the reaction between the reactants urea and water, yielding the products carbon dioxide and ammonia, which can be excreted easily by the body.
Urease
Urea + Water ↔ Carbon dioxide + Ammonia
In this reaction, the enzyme urease helps the reactants (molecules that enter a chemical reaction), urea and water, combine with each other. The bonds between the atoms in urea and water break and then reform between different combinations of atoms, forming the products carbon dioxide and ammonia. When the reaction is over, urease is unchanged and can catalyze another reaction between urea and water.
 If you find yourself struggling to figure out which proteins are enzymes and which enzymes do what, here’s a helpful hint: The names of enzymes end with -ase and usually have something to do with their function. For example, lipase is an enzyme that helps break down lipids (fats), and lactase is an enzyme that helps break down lactose.
If you find yourself struggling to figure out which proteins are enzymes and which enzymes do what, here’s a helpful hint: The names of enzymes end with -ase and usually have something to do with their function. For example, lipase is an enzyme that helps break down lipids (fats), and lactase is an enzyme that helps break down lactose.
. . . while lowering activation energy
Enzymes work by reducing the amount of activation energy needed to start a reaction so reactions can occur more easily. On their own, reactants could occasionally collide with each other the right way to start a reaction. But they wouldn’t do it nearly often enough to keep up with the fast pace of life in a cell. Without enzymes, your body wouldn’t be able to, say, clear urea out of your body fast enough, leading to a toxic buildup of urea. That’s where the enzyme urease comes into play. It binds the reactants in its active site and brings them together in a way that requires less energy for them to react.
Because reactions can occur more easily with enzymes, they occur more often. This increases the overall rate of the reaction in the body. One way to understand how enzymes speed up reactions is to think about reactions in terms of energy. In order for a reaction to occur, the reactants must collide with enough energy to get the reaction going. In the urea and water example, the reactants would need to collide with each other in just the right way for them to exchange partners and form into carbon dioxide and ammonia.
 Whatever you do, don’t fall for the idea that enzymes add energy to reactions to make them happen. They don’t. In fact, they don’t add anything to a reaction; they just help the reactants get together in the right way, lowering the “barrier” to the reaction. In other words, enzymes don’t add energy; they just make it so the reactants have enough energy on their own.
Whatever you do, don’t fall for the idea that enzymes add energy to reactions to make them happen. They don’t. In fact, they don’t add anything to a reaction; they just help the reactants get together in the right way, lowering the “barrier” to the reaction. In other words, enzymes don’t add energy; they just make it so the reactants have enough energy on their own.
Getting some help from cofactors and coenzymes
Enzymes are proteins, but many need a nonprotein partner in order to do their job. Inorganic partners, such as iron, potassium, magnesium, and zinc ions, are called cofactors. Organic partners are called coenzymes; they’re small molecules that can separate from the protein component of the enzyme and participate directly in the chemical reaction. Examples of coenzymes include many derivatives of vitamins. An important function of coenzymes is that they transfer electrons, atoms, or molecules from one enzyme to another.
Controlling enzymes through feedback inhibition
Cells manage their activity by controlling their enzymes via feedback inhibition, a process in which a reaction pathway proceeds normally until the final product is produced at too high of a level. The final product then binds to the allosteric site of one of the initial enzymes in the pathway, shutting it down. (An allosteric site is literally an “other shape” site. When molecules bind to these “other” pockets, enzymes can be shut down.) By controlling enzymes, cells regulate their chemical reactions and, ultimately, the physiology of the entire organism.
 Feedback inhibition gets its name because it uses a feedback loop. The quantity of the final product provides feedback to the beginning of the pathway. If the cell has plenty of the final product, then the cell can stop running the pathway.
Feedback inhibition gets its name because it uses a feedback loop. The quantity of the final product provides feedback to the beginning of the pathway. If the cell has plenty of the final product, then the cell can stop running the pathway.
By inhibiting the activity of an initial enzyme, the entire pathway is stopped. The process of feedback inhibition prevents cells not only from having to use energy creating excess products but also from having to make room to store the excess products. It’s like keeping yourself from spending money on a huge quantity of food that you won’t eat and would just end up storing until it rots.
 Feedback inhibition is reversible because the binding of the final product to the enzyme isn’t permanent. In fact, the final product is constantly binding, letting go, and then binding again. When the cell uses up its stores of the final product, the enzyme’s allosteric site is empty, and the enzyme becomes active again.
Feedback inhibition is reversible because the binding of the final product to the enzyme isn’t permanent. In fact, the final product is constantly binding, letting go, and then binding again. When the cell uses up its stores of the final product, the enzyme’s allosteric site is empty, and the enzyme becomes active again.